今更、マンデル＝フレミング・モデル再考②：水平なLM曲線と開放経済

今回は、水平なLM曲線を持つIS-LMモデルを開放経済に拡張したマンデル＝フレミング・モデル（MFモデル）について。通常、MFモデルは、IS-LMモデルにBP（Balance of payment : 国際収支)曲線を導入して、IS、LM、BPの３つの曲線から均衡条件を求めていくが、BP曲線の代わりにカバーなし金利平価を導入したほうが理解が容易である。

カバーなし金利平価

金利平価説とは、金利と外国為替レートに関する為替決定理論で、いずれの国で資金を運用しても全く同じ運用収益が得られると仮定する。

為替変動リスクがカバーされていないので、これをカバーなし金利平価と呼ぶ。

開放経済におけるIS-LMモデル(MFモデル）

開放経済におけるIS式は、輸出Xから輸入IMを差し引いた純輸出NXを加えることで得られる。

消費Cは、可処分所得Y－Tと共に増加する。投資Iは産出量Yと共に増加し、実質金利rが上昇すると減少する。政府支出Gは一定。輸出Xは外国の産出量Y*と共に増加するが、実質為替レートεが増価すると減少する。輸入IMは産出量Yと共に増加して、実質為替レートεが増価すると増加する。(1), (2)より

MFモデルはIS-LMモデルと同様に短期モデルであるので、国内外の物価水準は一定である。よって実質金利rは名目金利iと等しくなり、実質為替レートεと名目為替レートEは等しくなる。ゆえに上式は、

カバーなし金利平価を組み込んだ開放経済のIS-LMモデル(MFモデル）は次のようになる。

開放経済における政府支出増加の影響

中央銀行が政策金利を一定に維持すると仮定する。政府支出が⊿Gだけ増加すると、IS曲線は右にシフトして、均衡点はA1からA2に移り、産出量はA1からA2に増加する。右上がりのLM曲線の場合は、政府支出増加は金利上昇を齎し、自国の通貨高が生じるが、水平なLM曲線の場合には、金利は変化しないので為替レートは不変である。

細かく見ていこう。政府支出Gと消費Cは明らかに増える。投資Iは政府支出増加と共に増えるが、金利は一定の水準に保たれるので投資には影響しない。では純輸出NXはどうであろうか？　

外国の産出量Y*は所与とする。為替レートEは金利が一定に保たれるので変化しない。政府支出により国内産出量Yが増加すると、輸入Xが増えるので純輸出は減少する。

まとめると、
LM曲線が水平な場合、開放経済下での政府支出増加は、通貨高による純輸出の減少を引き起こさないが、国内への輸入増加から純輸出の減少は生じる、と言えよう。但し、金利クラウディング・アウトは起こらないが、実物クラウディング・アウトは起こりえる。

以上、二回に渡り、ブランシャール『マクロ経済学　第２版』で描かれている、水平なLM曲線を持つIS-LMモデルとそれを開放経済に拡張したMFモデルを解説してきた。現実の中央銀行は決してマネーサプライを操作しているわけでなく、政策金利を操作している。だから、水平なLM曲線は右上がりのLM曲線より妥当性が高いと思われる。水平なLM曲線は、マクロ経済学の教科書において今後のスタンダードになるかもしれない。そしていずれ金利クラウディング・アウトは消え去る運命にあるであろう。

追記：国内の金利と海外の金利は等しくなるのか？

今一度、カバーなし金利平価に立ち戻ろう。

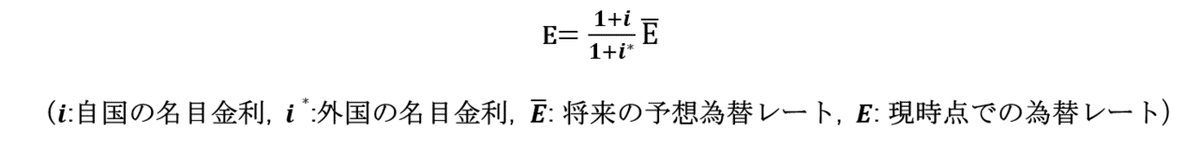
為替市場の参加者が、いつでも現在の為替レートの水準が今後も続くと考えると仮定した場合、将来の予想為替レートと現時点での為替レートが等しくなるので、上式より、i=i*。この場合、自国の名目金利と外国の名目金利が等しくなり、政府支出は完全にクラウデイング・アウトされてしまう。「いつでも現在の為替レートの水準が将来に渡って不変」という仮定はかなり特殊な仮定、まずはありえない仮定であろう。このことは留意されたし。