H26 機械 問15 同期電動機のトルクと誘導起電力
三相同期電動機の問題、やはり公式はしっかり使いこなせるようにならないといけないので、問題解くたびに書いておく。
T=Pₒ/ω・・・①
T:トルク[N•m]
Pₒ:出力[W]
ω:角速度[rad/s](2πN/60)
Pₒ=3E(V/x)sinδ・・・②
Pₒ:出力[W]
E:内部起電力[V]
V:電機子端子電圧[V]
x:同期リアクタンス[Ω]
δ:負荷角(EとVの位相差)[rad]
Nₛ=(120/p)×f・・・③
Nₛ:同期速度[1/min]
p:磁極の数
f:周波数[Hz]
設問で与えられているのは
・周波数f
・極数p
・端子電圧V
・電機子電流I
・力率cosθ
公式と見比べると、sinδが分かればトルクTを求められそう。
ここでδはEとVの位相差であり、
力率cosθが1なのでVとIのベクトルは同じ向き。
なのでEとVとIには次の関係が成り立つ。

Esinδ=xI・・・④
①に②③④を代入すると
T=Pₒ/ω
=3E(V/x)sinδ/(2πN/60)
=(3V/x)•xI/{2π•(120/p)×f/60}
=3V I/(4πf/p)
=3×(400/√3)×200/(4π×60/4)
=735.4[N•m]
よって(3)が正解。
(b)
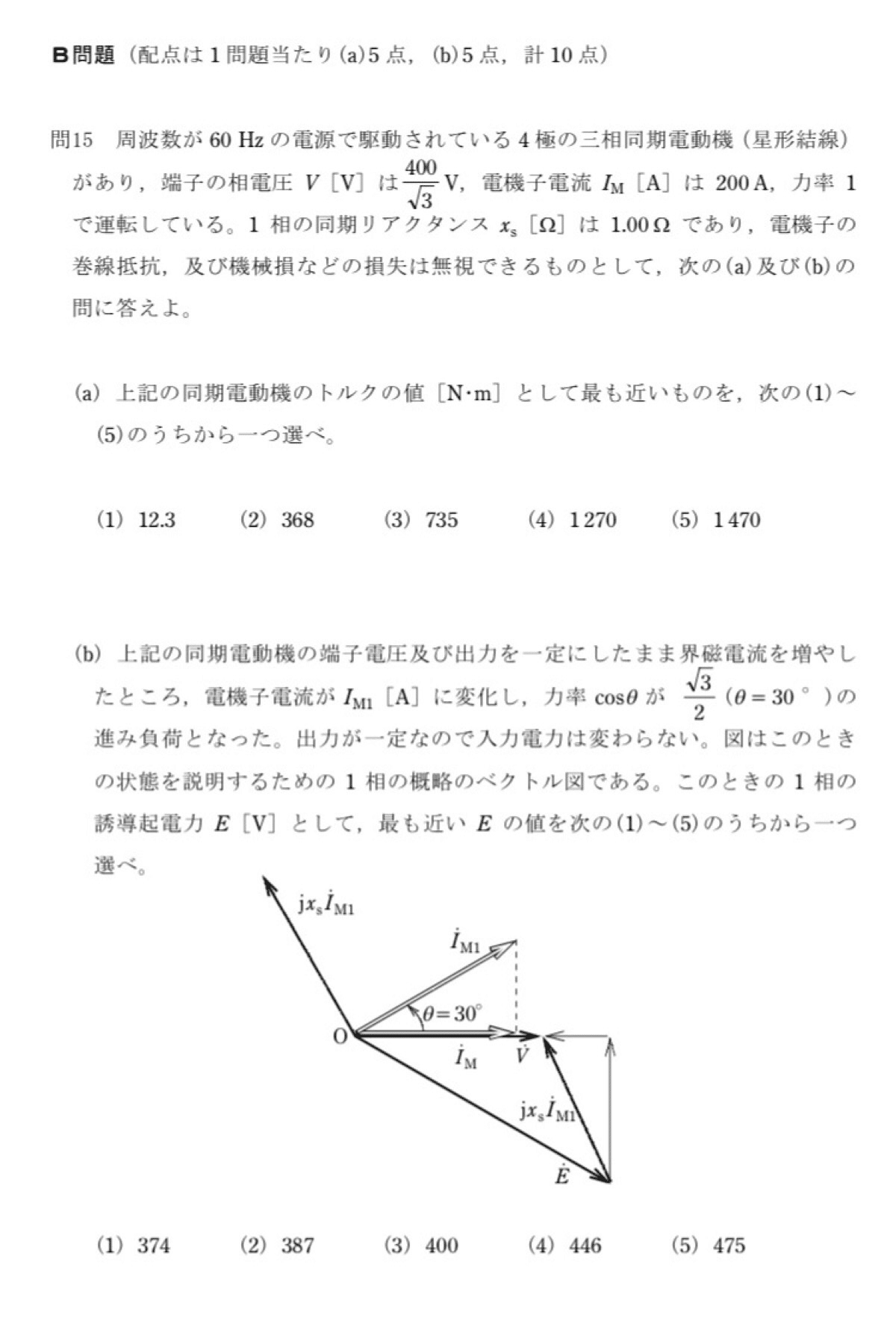
与えられたベクトル図より三平方の定理を用いて、
E=√{(V+xI'sinθ)²+(xI'cosθ)²}
と表せる。
ここで、出力一定なので電機子電流の有効値は変わらないことから、
I'cosθ= I
となり、θ=30°なので
I'= I÷cos30°
=200÷(√3/2)
=400/√3
これより、
E=√{(V+xI'sinθ)²+(xI'cosθ)²}
=√[{(400/√3)+1×(400/√3)×(1/2)}²
+{1×(400/√3)×(√3/2)}]²
=400[V]
よって(3)が正解。
いいなと思ったら応援しよう!

