ボールが1cm甘くなると、具体的にどれくらいヤバいのか、計算してみた。【卓球のための数学】
卓球は、甘いボールを送ってしまうと、打たれてしまいます。
「ボールが高くなってはいけない。」
「ボールが浅くなってはいけない。」
誰もが常に意識しています。
でも、
・どれくらい高くなるとヤバいのか
・どれくらい浅くなるとヤバいのか
って、けっこう曖昧ですよね。
だから、
「とにかく低く!」
「とにかく深く!」
と、とにかくギリギリを目指します。
それで狙い過ぎてミスをしてしまうわけです。
ならば、具体的にどこまでなら甘くなっても大丈夫なのかを知っていれば、ちょっとは気が楽になりますよね!?
ということで、早稲田大学教育学部数学科卒の、机上の空論大好き人間ホシナが、計算してみます!
ホシナの数字遊びに刮目せよ!
高さによるヤバさを検証
まずは、台から10cm浮いたボールは、相手にどれくらい強く打たれてしまうのか、見ていきます。
相手の打球の軌道が、下の図です。
卓球台は青で、打球の軌道は懐かしのオレンジボールで再現してみました。
ボールの中心がこの軌道を通っていると思ってください。
横軸(x軸)の0が相手コートのエンドラインです。
ここから相手が打ってきます。
x=156.8が、ネットの位置です。
x=313.6が、自陣のエンドラインです。
単位は「cm」で、対角線の長さです。
クロスに打ったイメージですね。
縦軸(y軸)も「cm」です。
y=15.25が、ネットの高さです。

(x,y)=(0,10)
ここが相手の打球点です。
エンドライン上の高さ10cmのポイントで打球しています。
なかなか前陣で、なかなか低いです。
(x,y)=(156.8,25.25)
ここで、ネットを越えています。
ボールの中心が25.25cmを通過すると設定しました。
ボールの底は23.25cmになり、ネットとの隙間は8cm、ボール2個分です。
なかなか低くて良いボールです。
(x,y)=(313.6,0)
ここで自陣にバウンドします。
ギリギリエッジではない、もしかしたらエッジかもしれない、深いところにバウンドしています。
この3点を通る放物線が、ボールの軌道になります。
まあまあ山なりなので、そこまで速いボールではなさそうです。
では果たして、この相手の打球のスピードはいかほどか、計算してみます!
まずは、この放物線の二次関数を、連立方程式で求めます。

そして、頂点の高さと重力加速度から、この放物線の球速を求めます。
空気抵抗はゼロ、回転もゼロ、重力は地球上の強さという設定です。
「真空の体育館で完全なナックルボールを打った」とイメージしてください。
イメージできますよね!?
計算方法は、分かる人は説明しなくても分かるし、分からない人は説明しても分からないので、割愛!

この相手の打球は、時速約28キロと分かりました。
決めに行くドライブが大体時速60キロあたりなので、かなり入れに行ったような打球です。
ちょっとだけ速めのフォア打ちくらいかなっていう感じです。
これだったら、象や牛が走った方が速いです。
やはり高さ10cmまで打点が落ちると、強く打つのは難しいわけですね。
では次に、ボールを甘くしてみましょう。
台からの高さを40cmに上げてみます。

軌道がかなり直線に近くなっています!
これは速そうですね。
では、計算をしてみましょう。

時速50キロを超えました。
これはしっかり強く打ったドライブなので、決まる確率は高いです。
到達時間は0.2秒。
人間の反応時間が0.1〜0.3秒なので、予測しないとブロックできませんね。
40cm浮くのはなかなかヤバいということが分かりました。
ではタイトル通り、1cm高くなるとどれだけヤバくなるのか、一気に見てみましょう!
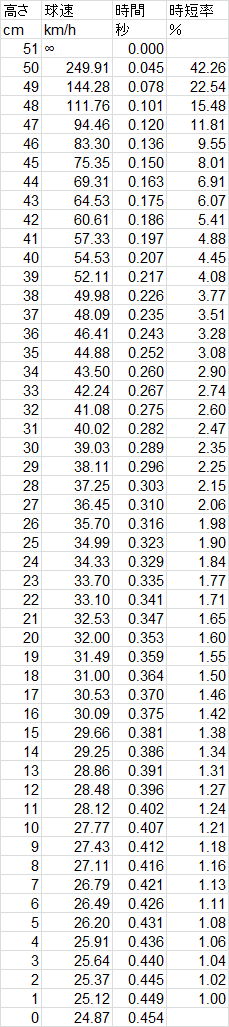
時短率に注目してください。
時短率とは、ボールが1cm高くなることによる、相手の打球の到達時間の短縮率です。
要は、この数値が大きいほど、
「1cm高くなったらヤバい」
ということです。
時短率を見てみると、ボールが高いほど、時短率が大きくなっています。
つまり、
「ボールが低いと、1cmズレようが大してヤバくない。」
「ボールが高いと、1cmのズレが大きく影響してヤバい。」
ということになります。
高さ40cmのときの数値を見てみます。
時短率は4.45%です。
高さ39cmのときと比べて、4.45%分強く打たれてしまうということです。
「なんだ、たったの4.45%か!」
「消費税の半分も無いじゃん!」
いやいや、これを甘く見てはいけませんよ。
例えば、サニブラウン選手は、100mを9.97秒で走ります。
これを、4.45%時短したらどうなるか。
なんと、9.53秒になります!
いきなりボルト越えの世界記録です!
いきなりそんなことになったら、もはやいろいろ疑っちゃいますよね!?
ボールが1cm甘くなるのは、それと同じだけの違いがあるのです。
ボールが浮いてしまう状況では、1cmだけでも低いボールを打とうとする努力が非常に重要だということがよく分かりました。
そしてもうひとつ、高さ51cmのときの数値を見てください。
なんと、球速無限のスマッシュが可能になります。
高さが50.5cmを越えると、ボールの軌道が完全な一直線でも入るようになります。
つまり、重力を利用する必要がなくなるので、時間なんてかけなくて良くなるのです!
なので、50.5cm以上の甘いボールを送ってしまったら、球速無限スマッシュを覚悟して、頑張ってブロックしてください。
もしノータッチで抜かれてしまっても、地球を一周してまたボールが来るかもしれないので、それを狙いましょう。
浅さによるヤバさを検証
では続いて、ボールの浅さがどう影響するのか、見ていきます。
まずは、高さy=5cmの低いボールで見ていきます。
x=80cmの浅いボールに対する相手の打球と、
x=-80cmの深いボールに対する相手の打球が、
下の図になります。


上の方が山なりなので、ボールは遅そうです。
でも、下の方が距離がある分、到達に時間がかかりそうです。
実は、軌道の頂点の高さで到達時間が決まるんですが、同じくらいに見えますね。
では、浅くなるとどれくらいヤバいのか、今回は4cmごとに見ていきます!
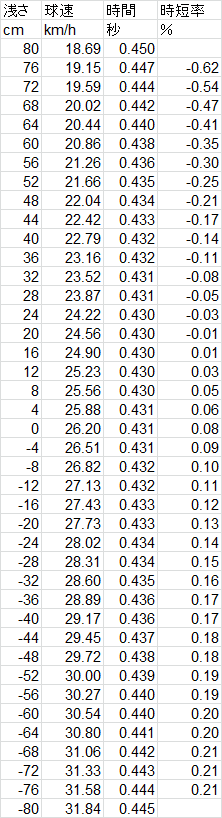
ここでの時短率とは、ボールが4cm浅くなることによる、相手の打球の到達時間の短縮率です。
なんと、浅さx=20cmからは、時短率がマイナスになっています!
時短率がマイナスということは、むしろ時間がかかるということです。
つまり、浅さx=20cm以上なら、浅ければ浅いほど相手は返球に時間がかかるのです!
しかも、x=80cmの浅いボールの方が、x=-80cmの深いボールよりも、相手は返球に時間がかかっています。
卓球は、低くて浅いボールが最強ということです!
とはいえ、どの浅さでも球速は遅く、到達時間は大差ありません。
乱暴に言うと、
「低いなら、深い浅いはどうだっていい!」
って感じです。
ただ、はっきり深いかはっきり浅いとより良いので、どちらにしてもはっきり狙いましょう。
では続いて、高さをy=35cmに上げてみます。
x=80cmの浅いボールと、x=-80cmの深いボールに対する軌道を見てみましょう。


上はかなり直線的な軌道です。
上から叩きつけたような、速そうな軌道です。
下はやや弧を描いています。
一生懸命打ったけど、遠いからなかなか、って感じです。
では、4cmごとの数値を見ていきます。
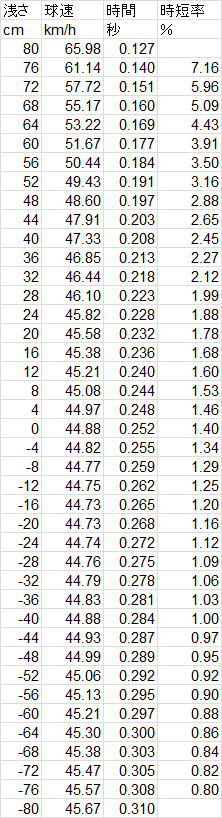
50cm以上浅くなると、時短率がはね上がっています。
やっぱり浅くて高いボールは、思いきり打たれてしまいますね。
台から出ている部分は、どこから打っても球速は大体同じです。
なので単純に、距離があるほど到達に時間がかかっています。
なので、どうしても打球が甘くなってしまうときは、深いところを狙うように心得ましょう。
また、打つ側としては、
「なるべく前で打った方がお得!」
ということになります。
わざわざ台から下がってドライブを打つのは、気持ちいいかもしれませんが、到達時間はかかってしまうので、損をしていると言えるでしょう。
高さ×浅さによるヤバさを検証
では次は、ヤバさの全体像をサーモグラフィー的に見ていきます。
これまでと同じく、縦軸が高さを、横軸が浅さを表しています。
球速

↓全ての数値が見たい方は、画像をダウンロードしてください。
y=30cmより低い部分は、浅さに関係なく割と安全なゾーンになっています。
そして、低くて浅いところに、時速20キロ未満の奇跡のゾーンがあります。
全部ここに行けたら最高なんですけどね。
y=45cmになると、x=80cmの浅いところでは完全にレッドゾーンになります。
チーターが襲ってくるようなスピード感で来るので、もう完全にヤバいです。
しかし、x=-80の深いところだと、まだ緑のゾーンなので、全然なんとかなります。
やや高いボールになると、浅さがかなり重要になってくるわけですね。
時間

こう見ると、完全に深いボールの方が良いですね。
ネットより高い部分では、明らかに深いボールの方が返球に時間がかかるのが分かります。
y=40cmの高さだと、x=-80cmの深いところでは緑のゾーンなので、ブロックは全然できます。
しかし、x=56cmより浅くなるとレッドゾーンに突入し、0.1秒未満でボールが飛んできます。
人間の反応時間は、0.1〜0.3秒です。
人間を辞めるか。
深いところを狙うか。
お好きな方をどうぞ。
縦比較

ボールが1cm高くなることによる時短率です。
断層みたいなきれいなグラフになりました。
浅いほど時短率が大きくなっています。
浅く打つときほど、低さに注意しないといけませんね。
横比較

ボールが4cm浅くなることによる時短率です。
ネットより低い台上の部分は、時短率がマイナスの極薄紫ゾーンが占めます。
ここだけは、短ければ短いほど、遅いボールが来ます。
y=30cmくらいまでは紫で覆われているんで、浅かろうが深かろうがさほど影響はありません。
しかしy=35cmを越えると、急にレッドゾーンが絡んできます。
「ネットの高さの2倍」のこのあたりに、意識すべきボーダーラインがありそうですね。
結論
卓球台の反発係数は約0.66だそうです。
(https://www.jst.go.jp/cpse/jissen/pdf/houkoku/TK160003-A-16009.pdf#search='%E5%8D%93%E7%90%83%E5%8F%B0+%E5%8F%8D%E7%99%BA%E4%BF%82%E6%95%B0')
大体3分の2ですね。
つまり、自分の打球の頂点が30cmなら、バウンドした次の頂点は20cmになります。
そして今回の計算で、相手の打点の高さがy=30cm以下なら割と安全だということが分かりました。
なので、自分の打球の頂点が45cm以下なら、次の頂点が30cm以下になります。
結論:ネットの高さの3倍までは、浮かせても割と大丈夫です!
まぁ、これは「真空体育館でナックルボールを打つ」という設定です。
現実では上回転をかけて打つので、もっと低いボールでも強打できてしまいます。
しかし、y=30cmぐらいの高さだったら、打ちミスが出ることも十分に考えられます。
なので、結果的に打たれるかはともかく、意識としては
「ネットの3倍まではオッケー!」
っていう感じで良いんじゃないかなと思います。
ネットの3倍をベースにして、いけそうならもっと低いところを狙うようにすれば良いでしょう。
あと、これはあくまで「頂点の高さ」であって、「ネットを越えたときの高さ」ではありません。
ネットを越えたときの高さは、2~2.5倍くらいが限界かもしれません。
次に、ストップについて考えます。
↓僕のツイートです。
☑️ストップは「低さ」を重視してください。
— 卓球研究家 星名勇太 (@TableTennisinst) February 3, 2020
いくら短くても、高ければ打たれます。
低ければ、最悪台から出ても、強打されることはありません。
ストップ練習をしていると、つい「短さ」を極めたくなってきます。
しかし、「狙い過ぎる」という状態は必ず大量のミスを生み出します。
今回の計算の結果、高さがy=20cmを越えると、浅いボールほど相手の打球の到達時間が短くなってしまうことが分かりました。
つまり、ストップの「短さ」を極めたところで、それが20cmより高くなってしまったら、完全に逆効果なのです!
浅く打つことでこちらが有利になるのは、ボールがネットより低いときだけです。
そしてボールが低ければ、多少長くなっても強打はされません。
つまり数学的に、ストップは「短さ」よりも「低さ」を重視すべきなのです!
次は中陣についてです。
卓球は、やっぱり前陣でできた方がいい。
— 卓球研究家 星名勇太 (@TableTennisinst) February 9, 2019
ドライブを打ちながら下がってしまう人が多い。
これだと、ブロックが甘く来たときに、打点が落ちて難しくなってしまう。
時間を作るために下がるわけだが、相手も時間ができるので、相対的にはプラスにならない。#卓球
今回の計算で分かったのは、
「台から離れると、明らかに強いボールが打てない」
ということです。
打点がx=0のエンドライン上だと、高さがy=41cm以上だと、到達時間0.2秒以下の強いボールが打てます。
しかし、x=-80のかなり離れたところから打つと、高さがy=52cm以上にならないと、到達時間0.2秒以下のボールは打てません。
明らかに敷居が高くなっています。
わざわざ自分から下がって、時間を確保してドライブを打ちたがる人がいますが、それは得策とは言えません。
確かに、球速は上げられるかもしれません。
しかし、それは残念ながら、広がった距離を補うには至らないのです。
次は、チャンスボールについてです。
チャンスボールではない球を、焦って強打しないようにしよう。
— 卓球研究家 星名勇太 (@TableTennisinst) August 25, 2019
無茶をしてしまううちは、勝つのはなかなか難しい。
甘いボールが来ても、自分の対応が間に合わず打点が落ちてしまったら、それはもうチャンスボールではないので繋いだ方がいい。#卓球
打点がボール1個分落ちるのがどれだけ致命的か、今回の計算でよく分かりました。
x=0cmのエンドライン上で打つとき、
高さがy=45cmだと、時速75.35キロのボールが打てます。
これがボール1個分落ちてy=41cmになると、時速57.33キロのボールしか打てません。
打点がボール1個分落ちるだけで、球速が24%も落ちるのです!
なのでこの場合、打点がボール1個分落ちたら、力を24%抜かないといけません。
そのままの力で打ってしまうと、そりゃミスをします。
打点の落ちた「チャンスボールだった球」には、慎重に対応するように心がけてください。
最後に
今回の計算で、
「打点をボール1個分落とさせる」
ことの重要性がよく分かりました。
球速24%OFFになるわけですから。
では、どうすれば相手の打点を落とさせることができるでしょうか。
それは、
「相手が待っていないボールを打つこと」
です。
もしストップが浮いてしまっても、相手がストップを予測していなければ、対応が遅れて打点が落ちます。
打点が落ちた時点で、時短率がマイナスの良いボールになります。
もしツッツキが浮いてしまっても、相手がそのコースを待っていなければ、対応が遅れて打点が落ちます。
相手は力加減を24%OFFしないと、打ちミスをします。
もしドライブを打っても、相手がそのコースを待っていれば、頂点で打てます。
ドライブの頂点はまあまあ高いので、カウンターを食らってしまいます。
このように、相手の打点を落とさせるには、相手の予測を外すことが重要になります。
ノータッチで抜くような、奇想天外な予測外しは必要ありません。
「ボール1個分の予測外しで十分。」
これを心がけましょう。
さぁ、今回のホシナの数字遊びはここまでです。
みなさん今日から、今回のサーモグラフィー的グラフを卓球台の空間に思い描きながら、練習してみてください。
この記事が気に入ったらサポートをしてみませんか?
