「ミスが多い方が、ミスが少なくなる！？」なんてことがあり得るんです！【卓球パラドックス】

世界ランキング１位以外の全ての皆さんに朗報です。



今回は、

「ミスが多い方が勝つ！？」

という、不思議な現象をご紹介します。



例えば、

0-11
0-11
11-9
11-9
11-9

のように、総得点が少なくても勝つことはできます。

しかし、今回紹介するのはそういうことではありません。



一見自分の方がミスが多いのに、総得点で勝てちゃうことがあるんです！

格下が勝てちゃうんです！

一体どういうことか、早速【問題】をどうぞ！

【問題】

AさんとBさんが、11点1ゲームの試合をしました。

「フォアハンドでミスをした確率は、Aさんの方が10％以上高かった」
「バックハンドでミスをした確率は、Aさんの方が10％以上高かった」

というとき、

「全体(＝フォアハンド+バックハンド)でミスをした確率は、Aさんの方が低かった」

つまり、

「Aさんが勝った」

ということは、あり得るでしょうか？

フォアハンドもバックハンドもAさんの方が下手なのに、それを合計するとAさんの方が上手くなっているなんて、あり得ないように思えますよね。



だって、テストで国語の点数も数学の点数も負けているのに、合計点は勝っちゃうなんて、おかしいわけです。

同性にも支持されていないし、異性にも支持されていないモデルは、合計しても支持されているはずはなく、ただの嫌われ者に決まってるはずです。



一方ももう一方も下回っているのに、合計すると上回るなんて、あり得ないような気がします。

でも、これがあり得ちゃうんです！



では、実例をご紹介しましょう。

【実例】

まず、AさんとBさんのフォアハンドを比較します。

Aさんは、16回打って6回ミスしました。
ミスした確率は6÷16＝37.5％です。

Bさんは、4回打って1回ミスしました。
ミスした確率は1÷4＝25％です。

Aさんの方が、12.5％高い確率でミスをしています。



次に、AさんとBさんのバックハンドを比較します。

Aさんは、4回打って3回ミスしました。
ミスした確率は3÷4＝75％です。

Bさんは、16回打って10回ミスしました。
ミスした確率は10÷16＝62.5％です。

Aさんの方が、12.5％高い確率でミスをしています。



確かに、フォアハンドもバックハンドも、Aさんの方が10％以上高い確率でミスをしています。

では、これを合計したらどうなるでしょう。

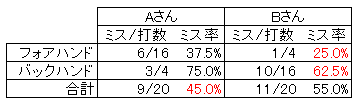
なんと、合計すると、Aさんの方がミスをする確率が低くなっています！

そして、Aさんのミスが9本、Bさんのミスが11本なので、11-9でAさんの勝利となります！



一体なぜ、こんなことが起こるんでしょう？

それは、

「Aさんはミスの少ないフォアハンドを多く打っていて、Bさんはミスの多いバックハンドを多く打っている」

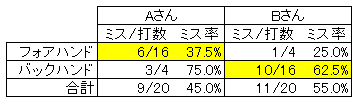
からです。

そして、

「AさんのフォアハンドとBさんのバックハンドを比べると、Bさんのバックハンドの方がミスをする確率が高い」

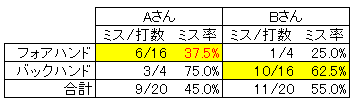
ので、Aさんは勝つことができたのです。



より理解しやすくするために、例を極端にしてみましょう。

【極端な例】

Aさんは、フォアハンドを1000回打って、1回ミスをしました。
Bさんは、バックハンドを1000回打って、999回ミスをしました。

ストレートでラリーをし続け、Bさんがミスをしまくったわけですね。

この時点で、表はこんな感じです。

999-1で、Aさんがボロ勝ちしています。

ここで、次に逆のストレートでラリーをして、Bさんのフォアハンドは入り、Aさんのバックハンドはミスをしました。

Bさんに1点が入りますが、当然、逆転には至りません。

この時点で、表はこんな感じです。

なんと、フォアハンドもバックハンドも、ボロ勝ちしているAさんの方が、ミスをする確率が高くなっています！



でも、Aさんはミスの多いバックハンド(ミス100％)をほとんど打っていないので、全体にはほとんど影響しません。

Bさんはミスの少ないバックハンド(ミス0％)をほとんど打っていないので、全体にはほとんど影響しません。

こうした打数の偏りが、このようなねじれた結果を生み出すのです。



これは、「シンプソンのパラドックス」と呼ばれるものを、卓球バージョンにアレンジしたものです。

気になる方は調べてみてください。

結論

強そうな相手と試合をするとき、

「フォアドライブも相手の方が上手いし、バックドライブも相手の方が上手いし、フォアブロックも相手の方が上手いし、バックブロックも相手の方が上手いし…」

と、全ての技術で相手の方が上手いと、絶望してしまいます。



しかし、今回のパラドックスで分かった通り、諦めるのはまだ早いです。

自分が一番得意なものを、相手が一番苦手なところにぶつけてください。



自分のフォアドライブが、相手のバックブロックより優れているなら、そこに勝機があります。

自分のフォアブロックが、相手のバックドライブより優れているなら、そこに勝機があります。

嫌われ者のモデルも、自分の異性の支持が、他のモデルの同性の支持を上回っているなら、そこに勝機があります。

全然モテない男性も、自分のアゼルバイジャン人女性に対するモテ度が、周りの男性たちの日本人女性に対するモテ度より高いのなら、そこに勝機があります。



自分の得意なフィールドと相手の苦手なフィールドを持ち出せば、弱者でも勝つことは可能なのです！



逆に、自分が一番得意なものが、相手の一番苦手なものにすら及ばないのであれば、それはもう絶望するしかありません。



自分の一番得意なフォアドライブが、相手の一番苦手なバックブロックに勝てないなら、もうどうしようもありません。

自分の一番得意な3球目攻撃が、相手の一番苦手なレシーブより劣っているなら、もうどうしたって3球目攻撃で勝つことはできません。

自分がいくらアゼルバイジャン人女性にモテようが、アンティグア・バーブーダ人女性にモテようが、セントビンセント及びグレナディーン諸島人女性にモテようが、グレートブリテン及び北アイルランド連合王国人女性にモテようが、結局横浜流星には敵いません。



残念ながらこんなときは、シンプソンのパラドックスに期待するだけムダです。

ムダな抵抗はやめて、潔く絶望しましょう。