「流れ」なんて虚構。6連続得点がいかに珍しくないか、計算してみた。【卓球のための数学】

卓球で、6連続で得点あるいは失点することってありますよね。

同レベルの人と試合をして、調子もメンタルも普通。

そんなときに6連続得点をすると、

「流れが良いぜ！」

6連続失点をすると

「流れが悪いなぁ。」

と思いますよね。

でも、よく考えてみると…「流れ」って、なんなんスかね？

「流れ」とは人間の創造物

人間は、説明のつかないことが起こったときに、架空の物を創造し、そいつに全責任を押し付けます。

（様々な責任を請け負ってくれる「幽霊」「お化け」に、人間は感謝しないといけません。）

そして、説明のつかないことが「説明できました！」と言って解明されたとき、その創造物は消滅します。

「地震」を例にあげましょう。

江戸時代は、急に地面が揺れるなんて意味が分かりません。

そこで江戸時代の人々は、

「地中の巨大ナマズが怒った」

という理由を創造して、納得していました。

そして後に、科学の力で「プレートがどうのこうの」と解明され、その瞬間に地中巨大ナマズは消滅したのです。

卓球の「流れ」も、同じだと僕は思うんです。

同レベルの人と試合をして調子もメンタルも普通なのに、6連続得点なんて有り得ないように思えます。

そこで「流れ」なんていう物を創造して、納得しているのです。

しかし、6連続得点は本当に有り得ないんでしょうか。

6連続得点が起こる確率って、実は低くないんじゃないでしょうか。

ということで、数学の力で「流れ」の正体を解明していきます。

数字遊びの始まりです！

（前回の数字遊び「9-11,9-11,9-11のストレート負けがいかに惜しくないか、計算してみた。」も是非ご覧下さい。）

計算開始…あれ？

まずは、実力が全く同じ2選手が試合をして、1ゲームで6連続得点が出現する確率を計算します。

その計算方法ですが、えーと、分かりません！

ちょっと激ムズが過ぎます。

正確な確率は、ちょっとゴメンナサイ。

とはいえ。

いろいろな角度からアプローチできるのが数学です。

何の計算もしないのはさすがにアレなので、ちょっとアプローチを変えて「ざっくり計算」をします。

まずは両選手の実力が等しいとして、「6回ラリーをして6連続得点が出現する確率」を計算します。

場合の数は2の6乗＝64通り。

そして6連続得点の出現数は「自分の6連続得点」と「相手の6連続得点」の2通り。

つまり6連続得点の出現率は2÷64＝約3％となります。

続いて「7回ラリーをして6連続得点が出現する確率」を計算します。

場合の数は2の7乗＝128通り。

出現数は以下の3パターン。

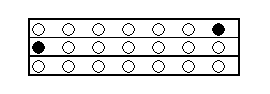
「自分」と「相手」で2倍して、6通りになります。

さらに、8回ラリーをする場合は、6連続得点の出現数は、

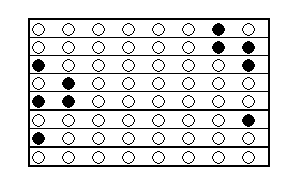
8×2＝16通り。

9回ラリーの場合は、

20×2＝40通りになります。

そんなこんなで計算した結果が、以下のとおりです。

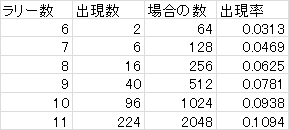
ラリー数を1回増やすごとに、出現率は大体1.5％上がります。

ラリーを11回やると、約11％の確率で、6連続得点が出現します。

この感じでいくと、ラリーを17回、つまり11-6でゲームが終わるとき、約20％の確率で6連続得点が出現することになります。

そしてこれを1試合で考えます。

1ゲームで6連続得点が出現する確率は20％。

出現しない確率は80％です。

ならば、フルゲーム（5ゲーム）で6連続得点が出現しない確率は、

0.8の5乗=0.32768

フルゲームで6連続得点が出現する確率は、

1-0.32768＝0.67232

計算結果

実力が全く同じ2選手がフルゲームを戦うと、

約67％の確率で6連続得点が出現します。

おっ、めちゃくちゃ高いですね！

ということは、6連続得点は「流れ」とかではなく普通に起こるということになります。

さて、これはあくまで「ざっくり計算」の結果です。

完全な信頼はできません。

この数字は妥当なのか、実際にやってみます。

実際にやってみた

ここは、Excel卓球の試合会場。

調子の良し悪しも、メンタルの強弱も存在しない。

両選手は常に50％の確率で点を取る、無機質な勝負の世界です。

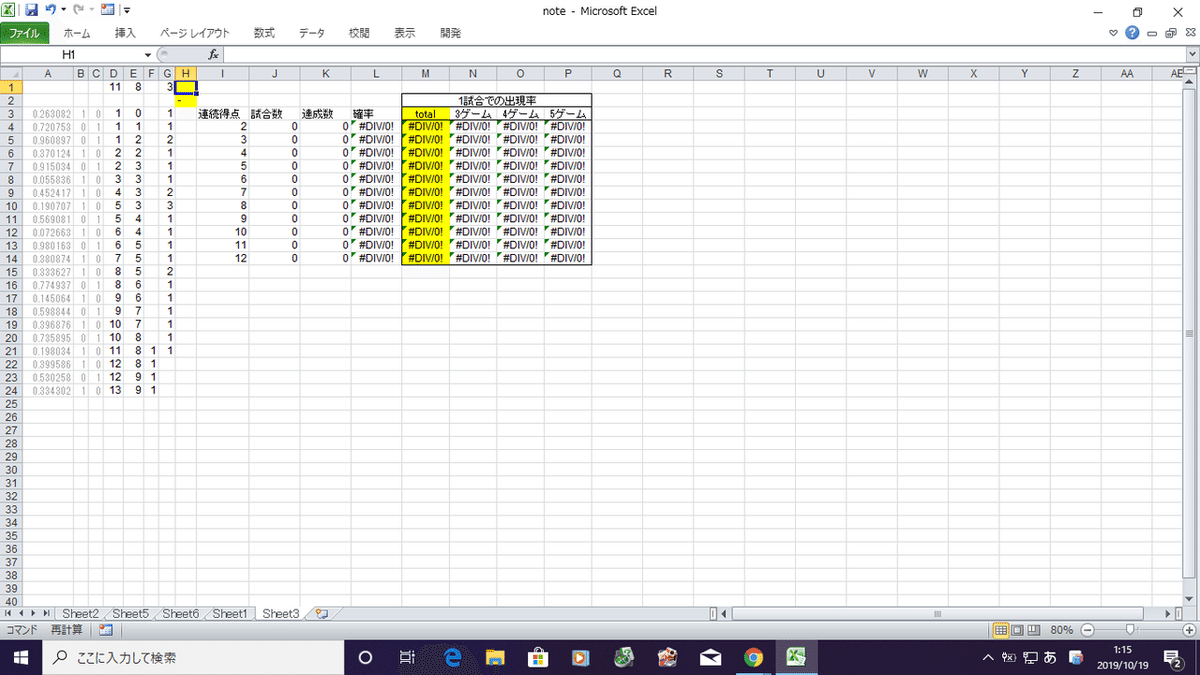
D列選手とE列選手が対戦します。

A列は、0以上1以下の数値がランダムで出ます。

これが0.5未満ならD列選手に1点、0.5以上ならE列選手に1点が入ります。

つまり、両選手の実力差は常に全く無い。

この状況で何連続得点が出るのか、見ていきます。

早速第1ゲーム。

11-9でD列選手が勝利。

最大の連続得点は3でした。

これをとにかく繰り返し、せっかくなので6連続得点だけでなく、2～12連続得点が出現する確率をはじき出します。

更新ボタン(F9)を押して第2ゲーム。

最大の連続得点は3でした。

ちなみに、卓球は12連続得点が可能です。

まず0-10まで追い詰められ、そこから12-10で勝つのが唯一の道です。

その出現率は、

2の22乗 分の 1 ×2=2097152 分の 1

です。

東京体育館に卓球台を210万台並べて、完全に実力が等しい420万人に試合をさせると、どこか1ヶ所で12連続得点が出現するイメージです。

では第3ゲーム。

4連続得点が出ました。

ちなみに、2連続得点が出現しないときは、交互に点を取り続けるときです。

これはこれでレアケースです。

11-11まで交互に点を取り続ける確率は、

2の22乗 分の 1 ×2=2097152 分の 1

で、12連続得点の出現率と同じです。

東京体育館に卓球台を210万台並べて、いや、よく考えたらスペースが圧倒的に足りなさそうですね。

月面に卓球台を210万台敷き詰めて、完全に等しい実力の420万人に試合をさせると、どこか1ヶ所で11-11まで交互に点を取り続けるイメージです。

そして第5ゲーム。

8連続得点が出ました。

実力差が無くても、こういうことは起こるということです。

表の右側では、「1試合での出現率」を計算しています。

1試合が3ゲーム、つまり3-0で勝つか負ける場合、連続得点が1度でも出現する確率は、

1-全く出現しない確率

=1-(1ゲームで出現しない確率)の3乗

(4ゲームなら4乗、5ゲームなら5乗になります。)

=1-((1-確率)の3乗)

となります。

さて、10ゲーム終了。

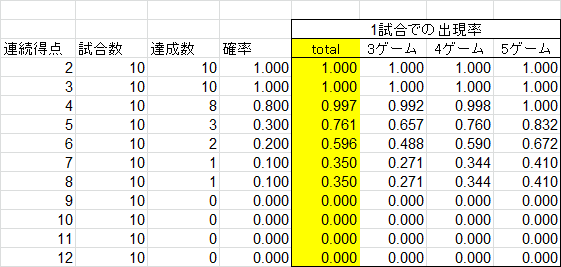
今のところ、6連続得点が出現する確率は20％です。

この場合、1試合3ゲームでの出現率は、

=1-((1-確率)の3乗)

=1-((1-0.2)の3乗)

=1-(0.8の3乗)

=1-0.512

=0.488

となります。

さて、50ゲーム終了。

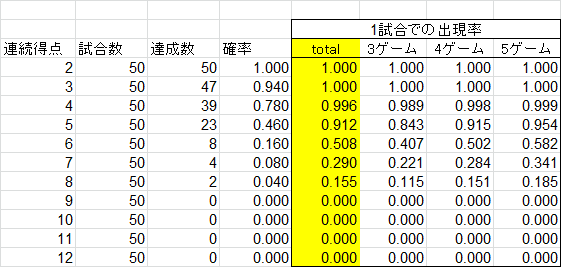
1試合での出現率の「total」は、最終の計算結果です。

1試合が3ゲームで終わる確率は25％。
1試合が4ゲームで終わる確率は37.5％。
1試合が5ゲームで終わる確率は37.5％。

これを考慮した、最終的な出現率です。

さて、僕はF9を押し続けます。

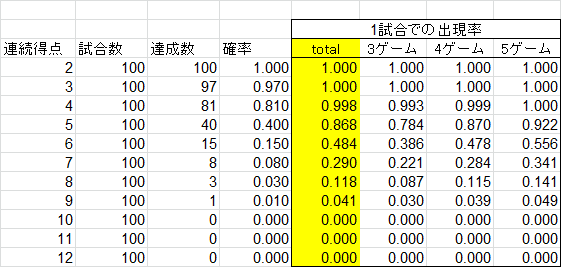
100試合。

まだまだF9を押し続け、

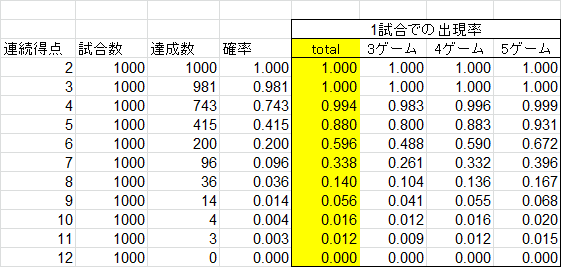
1000試合。

そして、F9を10分ほど押し続け、10000試合終了。

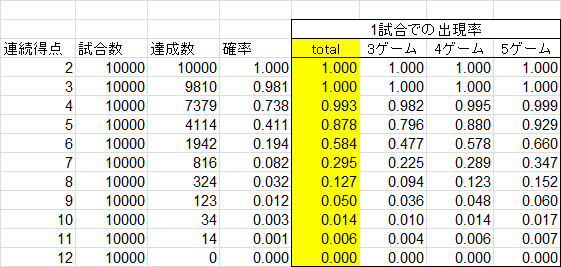
このような結果になりました。

1ゲームで6連続得点が出現する確率は19.4％となりました。

1試合での出現率は58.4％です。

実力差が全く無くても、半分以上の確率で6連続得点が発生するという結果になりました。

フルゲームでの出現率は66％で、ざっくり計算の結果とも大体合致していますね。

確認のため、もう一度10000試合やってみました。

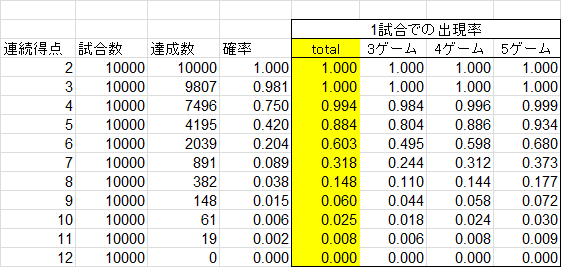
多少確率は上がりましたが、誤差の範囲内でしょう。

大体これくらい確率で間違いないと判断します。

結果

実力が同じ人と試合をすると、約6割の確率で、6連続得点は発生します。

そして、5連続得点の出現率は9割弱。
発生しない方がおかしいくらいです。

ちなみに、両選手の得点率を60％対40％に、実力差をつけて検証してみました。

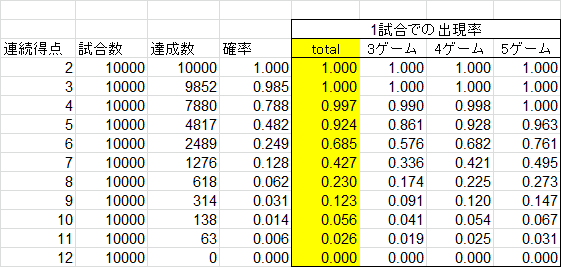
当然ですが、確率は上がりますね。

結論

同レベルの人と試合をして調子もメンタルも普通の状態でも、6連続得点は普通に起こることが、数学の力で解明されました。

よって「流れ」という創造物は、消滅しました。

もう、「流れ」と「地中巨大ナマズ」は同じカテゴリーの存在です。

では、「流れ」の正体を知った我々はどうすればいいのか。

連続得失点があっても気にしなければいいのです。

もちろん、調子やメンタルが原因の連続得失点は、対策が必要です。

しかし、理由の無い連続得失点はたまたまに過ぎないので、気にする必要はありません。

気にして自分の卓球が崩れてしまうのが一番いけないのです。

たまたま6連続失点したときに、

「流れが悪い！早く1点が欲しい！」

と、焦ってしまってはいけません。

たまたま6連続得点したときに、

「めっちゃ流れが良い！どんどん行こうぜ！」

と、調子に乗って攻めすぎて、ミスを連発してしまってはいけません。

たまたま6連続失点しても焦ラズ。
たまたま6連続得点しても調子に乗ラズ。
そういう者に
ワタシハナリタイ。