電験２種 平成25 理論　問4　複数の電源を持つRC回路　をエアギタリストがあえてラプラス変換で解いてみた

　別に一階線形微分方程式を解くスキルがあればラプラス変換する必要はないんだけど、微分方程式がめんどい、というサボリーマン向けにラプラス変換で解く方法です。
　ラプラス変換の魅力はなんといってもその速度、タイパです。変換さえできてしまえば計算が爆速になるので、対電験向けの有効な対策と考えています。逆に変換をミスるとクソ単純な計算ミスを犯す危険も孕んでいますが……微分方程式もその辺のリスクは同じような気がしています。
　つまりラプラス変換いちばんつおい。

では早速前提として……
①
tによって変化する関数xを解く際、変換をどうするか。
■　dx/dt　を単純に sX　に変換します■
　これ重要。結局、dナントカ/dtの形は、全てsナントカに変換してOKです。これが分かれば微分方程式がクッソ楽になります。

んで今回の問題ではv(t)を解くため
■C・ dv/dt　を　C(sV) 　に変換します■

②taira先生の動画により、方程式をαとβで単純化します。
※taira先生の動画を見てみてください。これだけでもめちゃくちゃ分かりやすいです。

以下動画より抜粋

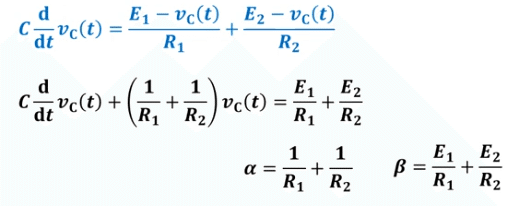
　↑問題文に青文字ママで方程式が出てると思いますが、このままラプラス変換するのはクソめんどくさいです。タイパが悪い。
　なのでtaira先生天才！　右辺の式をV(t)でくくって単純化します。この行為自体、部分分数分解的なチート感を感じて俺はテンションが上がります。
　変換後の式も動画で確認できます。

　ではこの簡素化された式をラプラス変換して爆速で解きます。

お分かりいただけただろうか。

逆変換さえ暗記していれば、１分かかりません。
あとはαとβを戻すだけ。

　あれ？　でもなんか 1/sがないのに1-になってるな……ま電験なら選択肢で絞れるからまぁいっか……
　いやこれ頭が=βじゃなくて=β/ｓっすね。βが定数からなのか理由は知らん。