【物理から考える気象】 収束・発散

はじめに

今回は「物理から見る気象」をテーマでnoteを書いてみることにした。

物理と気象？と思うかもしれないが、物理を専門に学んだ経験からすると、気象現象は物理現象そのものだ。

第一回は「収束・発散」を題材に書いてみる。

ベクトル解析

難しい数学を使って説明することはしないが、物理で使う言語は数学なので、まずは物理数学（物理のための数学）で習うベクトル解析の話をする。

ベクトル解析は物理学科の学生が、電磁気学のマックスウェル方程式を理解するために、必ず学ぶ必要になる数学。

ベクトル解析では、勾配：gradient（gradで表す）、発散：divergence（divで表す）、回転：rotation（rotで表す）の3つが登場し、下記のように定義される。

ここでｆは(x, y, z)の関数、Ａは(Ax, Ay, Az)で定義されるベクトルである。数学が苦手な人はこの時点で拒否反応を示しそうだけど、できるだけ簡単に説明する。

gradは今回のテーマではないのだが、難しくはないのでまずは説明しておく。

簡単な一次関数で考えてみる。関数ｆ(x, y, z)が

であれば（a, b, cは定数）、gradｆはそれぞれx, y, zで１回偏微分して、

となる。関数のx, y, z方向の傾き、変化率を示すベクトルとなる。偏微分が出てくるが、微分の授業でy=ax + bの関数があったら、aがグラフの傾きを示すことを思い出せば理解は難しくないだろう。

rotは次回のnoteにゆずるが、今回の本題のdivも難しいものではない。

縦、横、高さがdx, dy, dzの箱形の領域を考える。この領域を何らかの流れがあるとする。水の流れでもいいし、気流でも、電場や磁場でもいい。

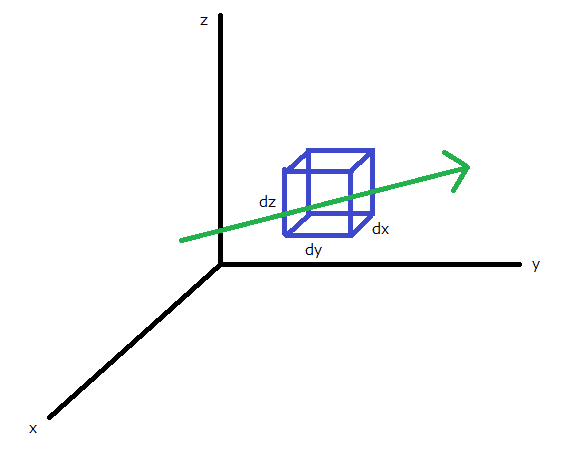
もう一度式を示すが、この流れがこの領域へ入る流量と出る流量の変化をX方向、Y方向、Z方向で計算して足したものがdivになることが式から理解できるだろうか。

右辺は順にAのX成分の変化量、Y成分の変化量、Z成分の変化量で、それを加算したものということ。

divがプラス（発散）になるということは、この領域内で流量が増えたこと（変化率がプラス）を意味するので、領域内を通過する際に流量を増やす何らかの作用があったことになる。

逆にこれがマイナス（収束）になるということは、この領域で流量が減ったこと（変化率がマイナス）になるので、領域内に流量を減らす何らかの作用があったことになる。

数学的、物理的に何を示すのかを説明するために少し数式を使ったが、収束、発散というものがどういう概念か理解できただろうか。

気象における収束と発散

以上は物理の話だったが、では気象では収束と発散をどう考えるのか？ 

気象で収束と言えば、高層天気図（例えば850hPa面）の風の流れにおいて、風が集まる場を収束といい、この領域では雲が発達しやすいと学ぶ。例えば、南寄りの温かく湿った気流と北寄りの冷たく乾燥した気流がぶつかりできる前線がそうだ。

気象の場合は例えば（u, v）の２次元の水平方向の気流のみで考える。ここで、uは東西（経度）方向、vは南北（緯度）方向を示す。divは下記のようになる。

風が収束しているところでは何らかの風量を減らす作用があることを意味する。ここでの作用は、吹く方向の違う（水平シアーがある）風がぶつかり、行き場を探して一部は上昇流となり、この等圧面から気流の流量を減らすことを意味する。

つまり、収束により上昇流が発生し、雲を発達を強化させることになる。

これが気象でいう収束を物理的観点から考察したものである。発散はその逆と考えれば良いだろう。

さいごに

今回は気象の収束・発散について、物理の視点から簡単に説明をしてみたつもりだ。

数学的なことは自分自身も思い出しながらだったりする。学生時代のようにバリバリと数式を計算できる状態に戻りたいと思っているが、もう無理だろうか？

次回は渦度とrotについてnoteにしたい。

【参考】
長沼伸一郎 著 「物理数学の直観的方法」
二宮洸三 著 「気象が分かる数式入門」