書記が数学やるだけ#45 ユークリッドの互除法と連分数の図解-1

小ネタとして，題通り「ユークリッドの互除法」と「連分数」の図解を試みることにする。今回は基本事項について扱い，次回東大の入試問題の準備とする。

問題

約分をする機会はたくさんあるが，これほど大きい数が約分できるのだろうか，単に約数を探そうにも見つからない。あえて(1)は即答できるようなものにしたが，「ユークリッドの互除法」と「連分数」を知っていると(2)も(3)も機械的に約分できるようになる。

ルート2については唐突感があるように思われるが，連分数を見ていくことでその関係性がわかると思う。無理数であることがポイントである。

公式

2つの自然数の最大公約数を求める方法として，ユークリッドの互除法が広く知られている。

なぜユークリッドの互除法がうまくいくのか，図解するとわかりやすくなると思う。幾何学的には，正方形による長方形の分割に該当する。

1段階ずつ見ていくと，次のようになる。

これで割り切れた。ユークリッドの互除法が終了したことに対応している。

さて，連分数についての話題に移る。

連分数を作るには，整数部分と小数部分に分け，小数部分の逆数を分母に持っていき，その中で整数部分と小数部分に分け，…を繰り返す。式をよく見てみると，ユークリッドの互除法に対応していることがわかる。

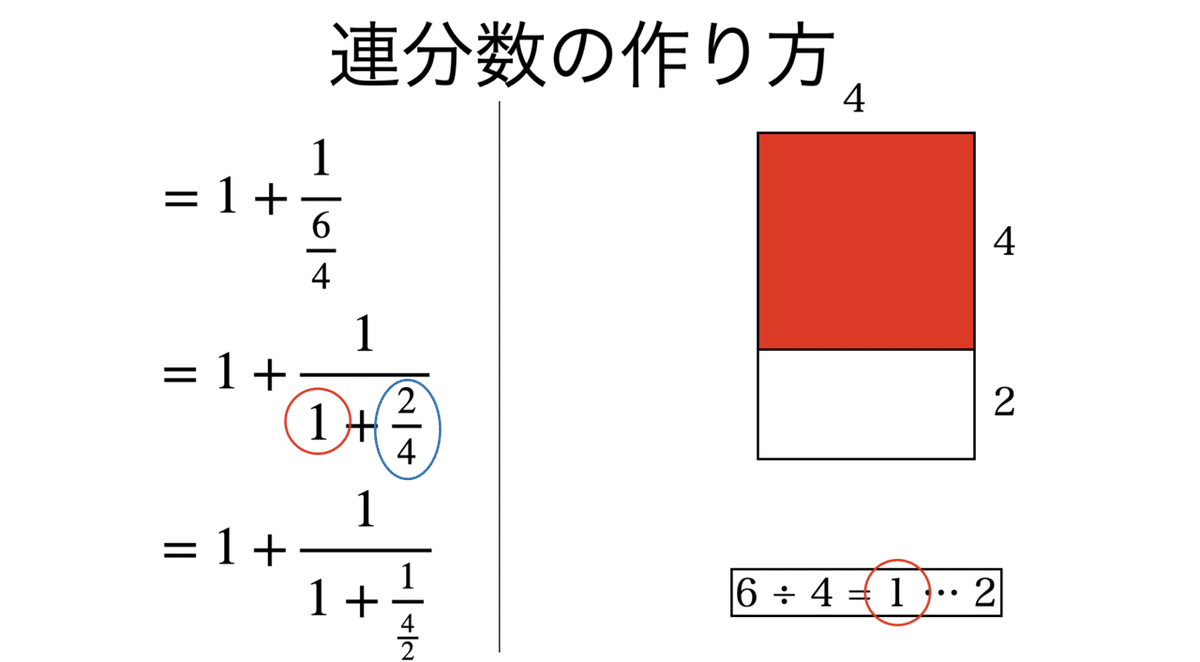
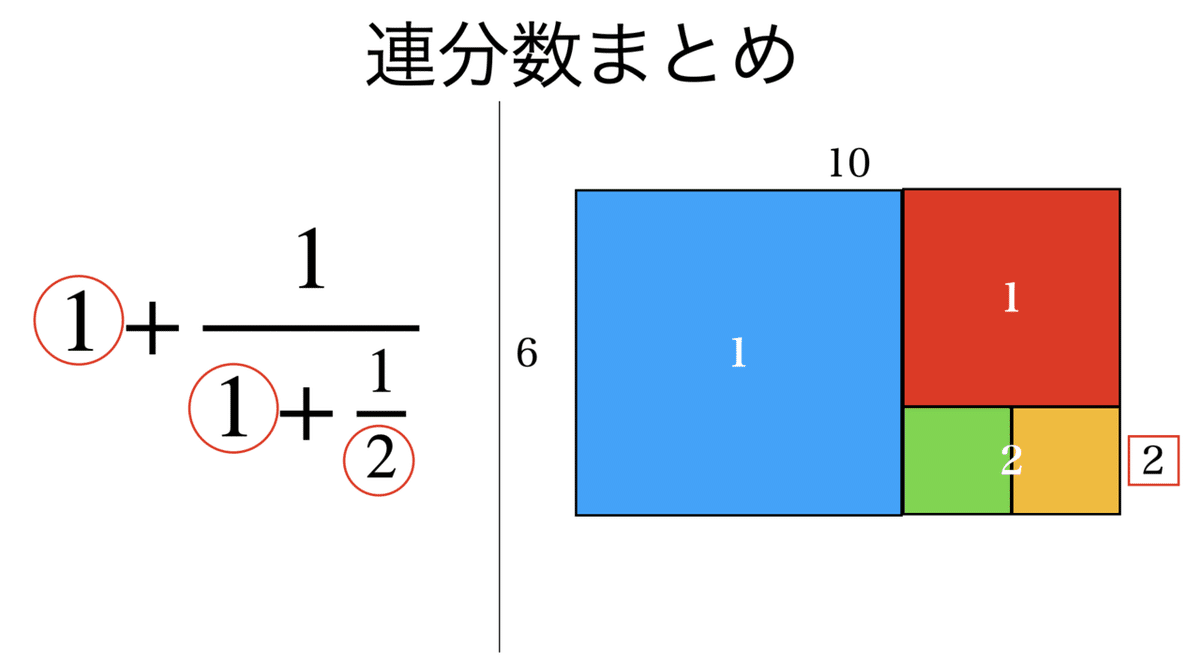
連分数とユークリッドの互除法の対応関係を見てきたが，これは有理数でいえる一般原則である。では，ルート2のような無理数ではどうかというと，連分数展開が終わることはない。

解法

(1)は既に例示したので(2)から。高校入試でも約分が単体で出ることもある。ユークリッドの互除法で最大公約数を求めて，分母分子を最大公約数で割ると既約分数になる。

これを連分数展開でやると以下のようになる。まずは連分数の形にする。

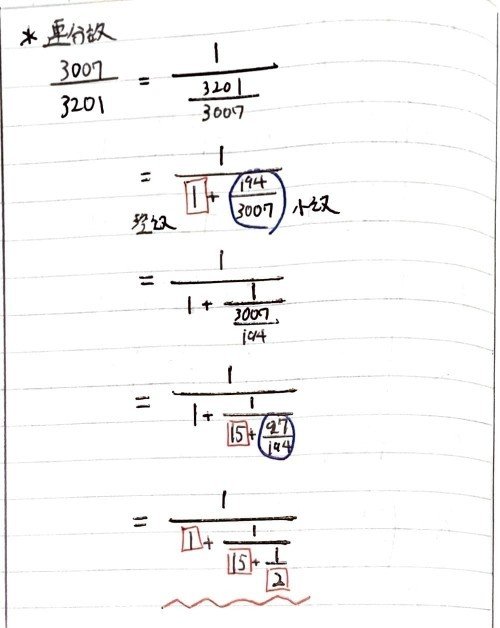
そのあと下から通分していくと，たしかに約分できている。

大学入試での約分の問題。ここまで来るとあからさまにユークリッドの互除法か連分数展開が浮かぶかどうかにかかってくる（しかもすぐに終わる）。

では無理数の連分数展開をしてみる。

ルート2を連分数展開すると，同じ操作の繰り返しに至る。つまり無限に続くということである。

これで基本は一通りさらえたので，次回はこれをもとに東大の問題を解説する。

本記事のもくじはこちら：