書記が数学やるだけ#706 ベクトル場の定義と演算

ベクトル場についての基本事項をまとめる。

問題

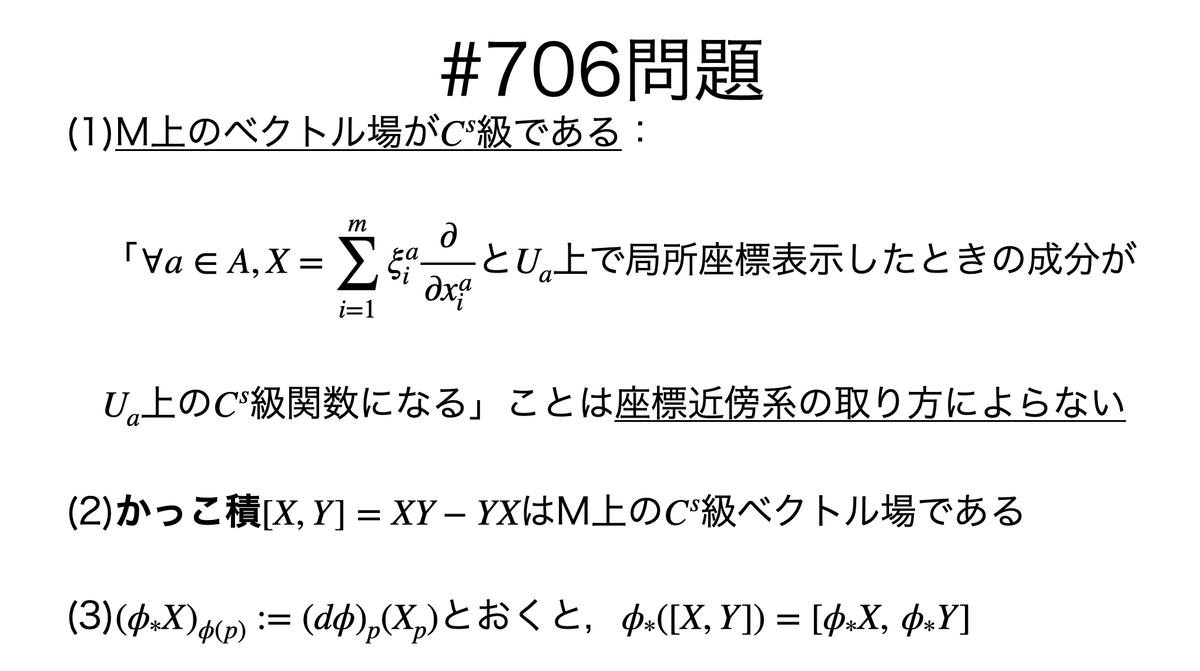
説明

ベクトル場は，多様体上の各店から接ベクトルへの対応と定義される。ベクトル場はさまざまな物理現象において有用なツールである。

ベクトル場の例として，リー代数におけるかっこ積を簡単に紹介する。

解答

C^r級多様体において，ベクトル場の微分可能性はC^r-1級以下においてのみ定義される。

1階の微分作用素X,Yに対し，XYやYXは2階作用素となるが，そのかっこ積XY-YXは1階の微分作用素となり都合が良い。

この計算は後に扱う引き戻しに関係がある。

本記事のもくじはこちら：