
【大学数学】群・環・体とは?①
1.はじめに
高校生の時に、複素数を学び、とても感動したのを今でも覚えています。概念の拡張がおもしろかったからです。そして、複素数が数の概念の拡張の限界だと思っていました。しかし、大学で数学を勉強し、そうではないことを知りました。群・環・体という王様がいたのです。複素数以上に感動しました。今回は、そんな群・環・体を紹介したいと思います。

2.数の概念の拡張
まずは、群・環・体の前に、数の概念の拡張について説明します。
自然数では、引き算ができない場合がある(2-3=?など)。そこで生まれたのが、負の数(2-3=-1)。そして、自然数と0と負の数をまとめて整数としました。
整数では、わり算ができない場合がある(2÷3=?など)。そこで生まれたのが、有理数(2÷3=2/3)。※整数も有理数です(2=2/1)。
有理数では、根が存在しない場合がある(2乗して3になる数?など)。そこで生まれたのが、無理数(2乗して3になる数は√3)。そして、有理数と無理数をまとめて実数としました。
実数では、方程式の解がない場合がある(2乗して-1になる数?など)。そこで生まれたのが、虚数(2乗して-1になる数はi)。そして、実数と虚数を複素数としてまとめました。
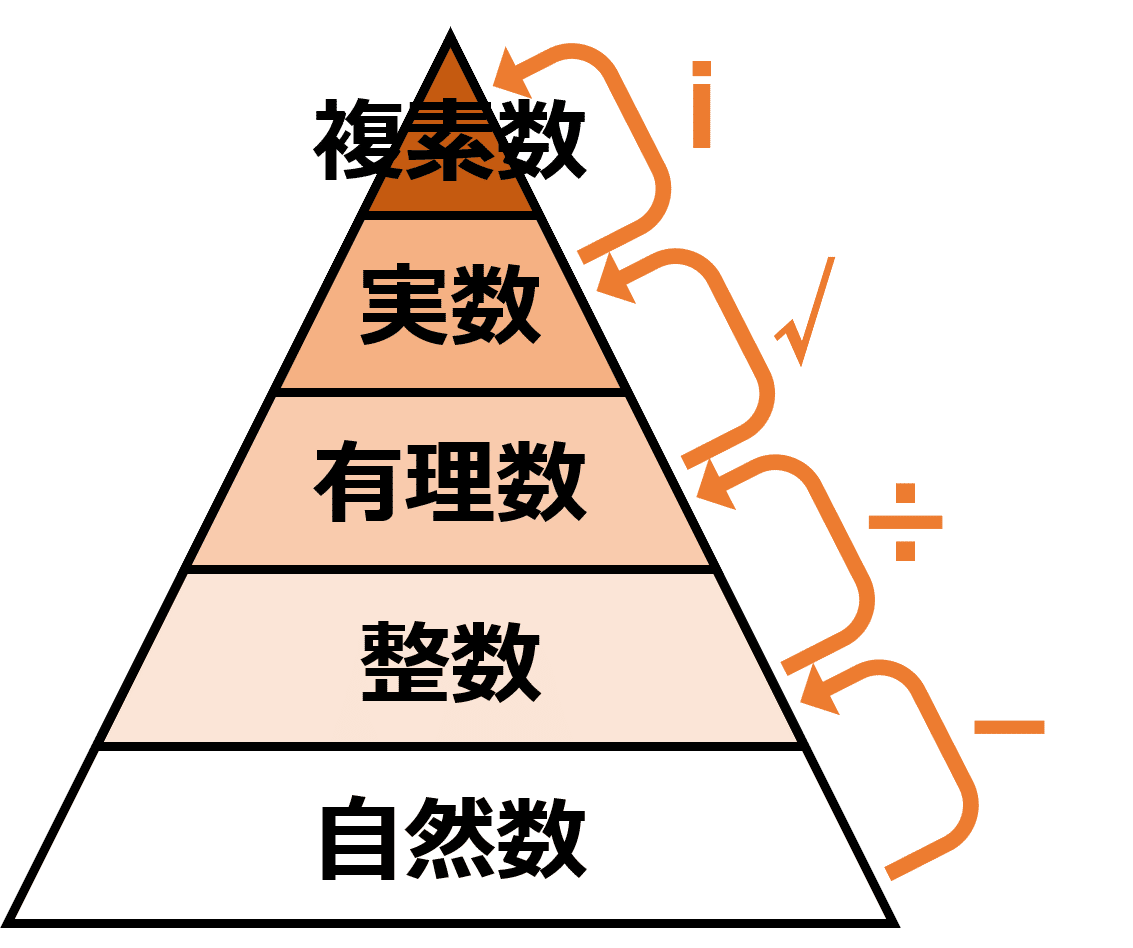
このように、数の概念の拡張がされていくのは、おもしろさがありますよね。そして、これよりももっと大きな概念が、群・環・体なのです。
3.群・環・体
では、群・環・体とは何なのか。簡単に説明すると、群は加法・減法について閉じている。環は加法・減法・乗法について閉じている。体は加法・減法・乗法・除法について閉じているものです。これを数以外のものにも考えるのです。数でいうと、下のようになります。
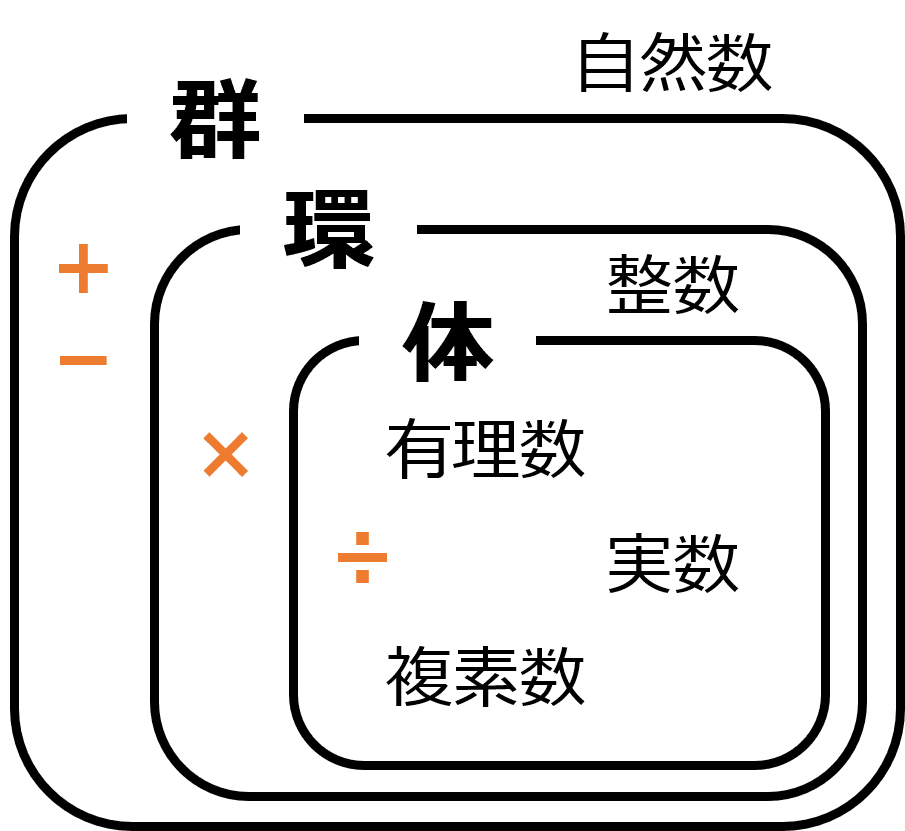
※閉じているとは、集合の元に対して演算を行ったときに、またその集合の元にもどることをいいます。
自然数は、減法について閉じていないので、群ではありません。整数・有理数・実数・複素数は、加・減・乗法について閉じているので、環です。特に、有理数・実数・複素数は、除法についても閉じているので、体です。
数以外にも考えると述べましたが、具体的には、行列や式、関数などです。
例えば、正方行列は、環をなします。加・減・乗法ができますよね。しかし、除法ができませんので、体ではありません。そして、正方行列でない場合、加法ができるとは限りませんので、単なる行列は、群をなしません。
また、多項式も環をなします。ただし、除法について閉じていないため、体をなしません。
他にもたくさん例がありますが、別の記事で紹介していきます。
以下は、群・環・体の詳細な定義とまとめになります。
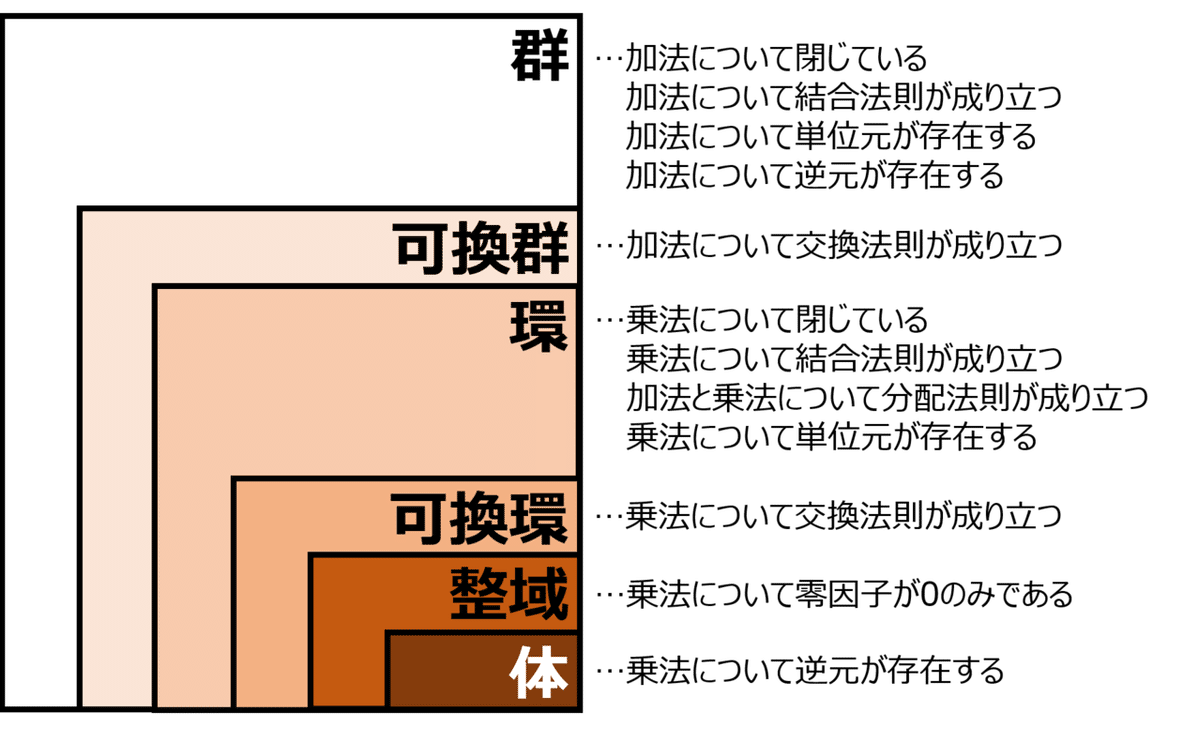
四則演算だけでなく、結合法則や交換法則などについても考えなくてはなりません。
ちなみに、四則演算について、群は加法についてしか記載がありませんが、加法についての逆元の存在が、減法を意味します。同様に、体は乗法についての逆元の存在が、除法を意味します。
※単位元とは、整数の加法でいうと0、乗法でいうと1です。 逆元とは、ある元に演算をして単位元になる元のことです。整数の加法でいうと、2の逆元は-2(2+(-2)=0)です。
4.おわりに
群・環・体とは、数以外にも、行列や式、関数などざまざまなものについて、演算を入れ、まとめ上げたものです。代数学の基本として研究されてきて、フェルマーの最終定理などを証明するのに大活躍しました。
大学数学では、このように、大きな概念の中で議論していきます。抽象的で難しいですが、大きな概念で物事を考えることで、世界が広がり、とてもおもしろいです。
