
【集合】3 集合どうしの演算とべき集合
こんにちは、これが307本目の記事となったすうじょうです。今日は、大学数学の解説記事です。今回の内容は、集合論より集合どうしの演算を解説します。本記事は大学数学の記事ですが、一部高校数学の内容を含みます。
この記事は、以下の記事の続きです。
全体集合(普遍集合)
部分集合などの議論をするときに、1つの定まった集合$${U}$$を考え、その中である条件を満たす要素からなる集合について考えることがある。このとき、$${U}$$を全体集合(普遍集合)という。以下に例を挙げる。
全体集合$${U=\{x|x \in \N\}}$$とするとき、その部分集合$${A=\{1,2,3\}}$$を考えると、ベン図は図5のようになる。
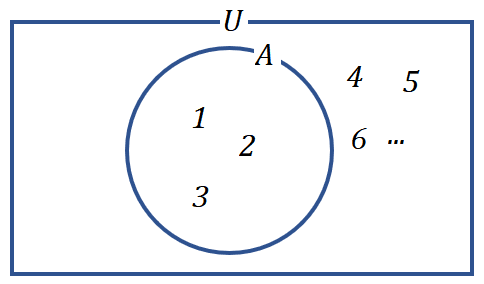
集合演算
和集合(合併集合)
2つの集合$${A,B}$$の少なくとも一方に属している要素の集合を$${A}$$と$${B}$$の和集合(合併集合)といい、$${A \cup B}$$と表す。この定義は以下のように書くことができる。
$${A \cup B = \{x|x \in A または x \in B\}}$$
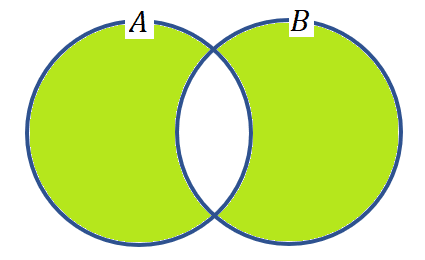
これをベン図で表すと図6のようになる。
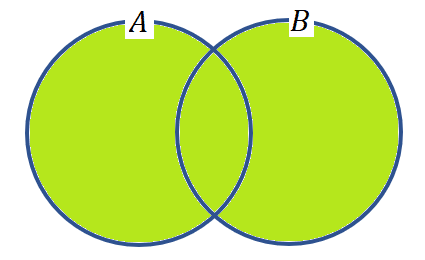
共通部分(積集合)
2つの集合$${A,B}$$のどちらにも属している要素の集合を$${A}$$と$${B}$$の共通部分(積集合)といい、$${A \cap B}$$と表す。この定義は以下のように書くことができる。
$${A \cap B = \{x|x \in A かつ x \in B\}}$$
$${A \cap B = \{x|x \in A, x \in B\}}$$
※内包的記法では「1 集合とは」でも書いたが「,」はかつを意味する。
これをベン図で表すと図7のようになる。
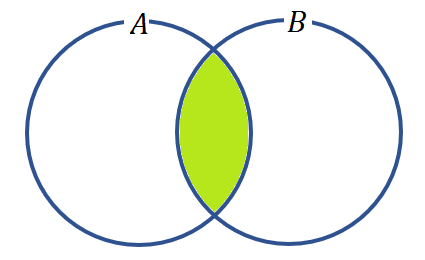
※積集合の記号について
共通部分は積集合とも呼ばれ、「積」という名前が付いているが、$${A \times B}$$とは書かない。$${A \times B}$$は後に扱う直積集合を意味し、まったく別のものなので注意する。
差集合・補集合
2つの集合$${A,B}$$について、$${A}$$には属するが$${B}$$に属さない要素の集合を$${A}$$と$${B}$$の差集合といい、$${A \setminus B}$$または$${A - B}$$と表す。この定義は以下のように書くことができる。
$${A \setminus B = \{x|x \in A かつ x \notin B\}}$$
$${A \setminus B = \{x|x \in A, x \notin B\}}$$
これをベン図で表すと図8のようになる。
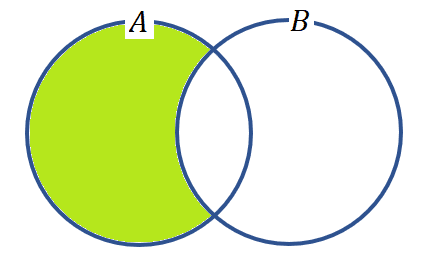
$${A \setminus B}$$は$${A}$$に対する$${B}$$の補集合ともいう。
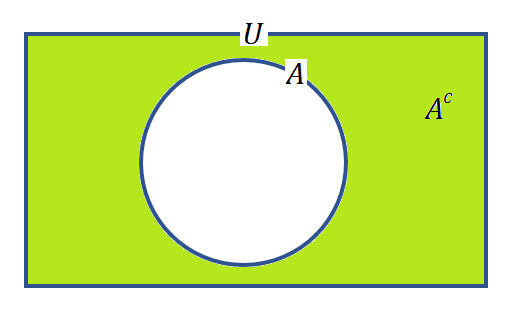
また、全体集合$${U}$$とその部分集合$${A}$$があるとき、全体集合$${U}$$に対する$${A}$$の補集合$${U \setminus A}$$を、単に$${A}$$の補集合といい、$${A^C}$$または$${\bar{A}}$$と表す。これをベン図で表すと図9のようになる。
対象差
2つの集合$${A,B}$$のどちらか一方にのみ属している要素の集合を$${A}$$と$${B}$$の対象差といい、$${A \triangle B}$$または$${A \ominus B}$$または$${A \oplus B}$$と表す。この定義は以下のように書くことができる。
$${A \triangle B = (A \cup B)\setminus(A \cap B)}$$
$${A \triangle B = (A \setminus B) \cup (B \setminus A)}$$
これをベン図で表すと図10のようになる。
集合演算の法則
ここでは、これまでに述べた集合演算についての法則をまとめて紹介する。証明については、省略するがそれぞれ演算の定義を用いれば求められる。
・同じ集合どうしの演算
$${A \cup A = A, A \cap A = A, A \setminus A = \empty, A \triangle A = \empty}$$
・空集合との演算
$${A \cup \empty = A, A \cap \empty = \empty, A \setminus \empty = A, A \triangle \empty = A}$$
・全体集合との演算
$${A \cup U = U, A \cap U= A, A \setminus U= \empty, A \triangle U= A^{C}}$$
・交換法則(演算の順序を交換できる)
$${A \cup B = B \cup A, A \cap B= B \cap A, A \triangle B= B \triangle A}$$
※差に関しては、交換法則は成り立たない。
・結合法則(演算の優先順位を変更しても結果は変わらない)
$${(A \cup B) \cup C = A \cup (B \cup C), (A \cap B) \cap C= A \cap (B \cap C), (A \triangle B) \triangle C= A \triangle (B \triangle C)}$$
・分配法則(演算は掛け算のように展開することができる)
$${A \cup (B \cap C)=(A \cup B) \cap (A \cup C), A \cap (B \cup C)=(A \cap B) \cup (A \cap C)}$$
・回帰法則
$${(A^C)^C=A}$$
・補元法則
$${A \cup A^C=U, U^C=\empty, A \cap A^C=\empty, \empty ^C =U}$$
・ド・モルガンの法則
$${(A \cup B)^C=A^C \cap B^C, (A \cap B)^C=A^C \cap B^C}$$
※ド・モルガンの法則に関しては、ベン図で考えるとわかりやすい。
共通部分と和集合の結合法則を一般化して、以下のような略記がされることがある。
$${n}$$個の集合$${A_1,A_2,A_3,…,A_n}$$に対して、
$${A_1 \cup A_2 \cup A_3 \cup … \cup A_n = \displaystyle\bigcup_{i=1}^n A_i}$$
$${A_1 \cap A_2 \cap A_3 \cap … \cap A_n = \displaystyle\bigcap_{i=1}^n A_i}$$
べき集合
集合$${A}$$の部分集合全体からなる集合をべき集合(冪集合)といい、$${2^A}$$または$${\mathcal{P} (A)}$$と表す。この定義は以下のように書くことができる。
$${2^A=\{X|X \subseteq A\}}$$
集合$${A}$$のべき集合の要素数は、集合$${A}$$の要素数を$${|A|}$$とすると、$${2^{|A|}}$$となる。(部分集合の個数と等しい)
演習問題3
問題7 次の集合演算の結果をそれぞれ求めよ。
(1)$${\{1,2\} \cup \{1,3,4\}}$$
(2)$${\{1\} \cup \{2,\{3,4\}\}}$$
(3)$${\empty \cup \{\empty\}}$$
(4)$${\{1,2\} \cap \{2,3\}}$$
(5)$${\{1\} \cap \{\{1\},2\}}$$
(6)$${\{\empty\} \cap \{\{\empty\}\}}$$
(7)$${\{1,2,3\} \setminus \{2,3\}}$$
(8)$${\{1,2\} \setminus \{1,2,3\}}$$
(9)$${\{a,b,\empty\} \setminus \empty}$$
(10)$${\{1,2,3\} \triangle \{2,3,4\}}$$
(11)$${\{\empty\} \triangle \{\empty, \{\empty\}\}}$$
[解答]
(1)$${\{1,2\} \cup \{1,3,4\}=\{1,2,3,4\}}$$
(2)$${\{1\} \cup \{2,\{3,4\}\}=\{1,2,\{3,4\}\}}$$
(3)$${\empty \cup \{\empty\}=\{\empty\}}$$
(4)$${\{1,2\} \cap \{2,3\}=\{2\}}$$
(5)$${\{1\} \cap \{\{1\},2\}=\empty}$$
(6)$${\{\empty\} \cap \{\{\empty\}\}=\empty}$$
(7)$${\{1,2,3\} \setminus \{2,3\}=\{1\}}$$
(8)$${\{1,2\} \setminus \{1,2,3\}=\empty}$$
(9)$${\{a,b,\empty\} \setminus \empty=\{a,b,\empty\}}$$
(10)$${\{1,2,3\} \triangle \{2,3,4\}=\{1,4\}}$$
(11)$${\{\empty\} \triangle \{\empty, \{\empty\}\}=\{\{\empty\}\}}$$
問題8 $${U=\{a,b,c,d,e\},A=\{a,c,d\}}$$,$${U}$$を全体集合とするとき、$${A^C, 2^A}$$をそれぞれ求めよ。
[解答]
$${A^C=U \setminus A=\{a,b,c,d,e\} \setminus \{a,c,d\}=\{b,e\}}$$
$${2^A=2^{\{a,c,d\}}=\{\empty,\{a\},\{c\},\{d\},\{a,c\},\{a,d\},\{c,d\},\{a,c,d\}\}}$$
※べき集合で、すべての要素を挙げることができているかどうかは、もとの集合の要素数から$${2^{|A|}}$$を計算して確かめるとよい。
問題9 $${A=\{a,\{b,c\}\}}$$とするとき、次の(a)~(f)のうち、正しいものをすべて選べ。
(a)$${\empty \in 2^A}$$
(b)$${\{a\} \in 2^A}$$
(c)$${\{b,c\} \in 2^A}$$
(d)$${\empty \subseteq 2^A}$$
(e)$${\{a\} \subseteq 2^A}$$
(f)$${\{\{\{b.c\}\}\} \subseteq 2^A}$$
[方針]
この問題で、集合論の解説記事1,2の内容も理解できているか確認できます
[解答]
$${2^A=\{\empty,\{a\},\{\{b,c\}\},\{a,\{b,c\}\}\}}$$より
(a),(b),(d),(f)
(c)は$${2^A}$$に$${\{b,c\}}$$という要素はないので、誤り
(e)は$${2^A}$$に$${a}$$という要素はないので、誤り
最後に
今回は、大学数学・集合論の解説記事として、集合どうしの演算とべき集合について解説しました。今回の内容は、様々な数学的な理論で出てくる集合を使った表現を理解するために必要な知識の一つです。この記事の続きとして、二項関係の基礎の解説記事を書く予定です。では。
この記事の続きは以下の記事です。
