
【集合】7 写像・関数と全射・単射など
こんにちは、これが335本目の記事となったすうじょうです。今日は、大学数学の解説記事です。今回の内容は、集合論より写像・関数を解説します。
この記事は、以下の記事の続きです。
ただ、前提知識としては上の記事よりも次の記事の内容の理解が必要です。
写像・関数
関数の簡単な説明
ここでは、高校まででされてきた関数の簡単な説明をいくつかしてみる。関数は中学数学で初めて登場した概念で、次のように説明された。$${x}$$の値を1つ決めると対応する$${y}$$の値が1つ決まるとき$${y}$$は$${x}$$の関数といい、$${y=f(x)}$$と表す。
また、次のようなイメージで説明されることもある。
関数は、「入力$${x}$$が入ると、出力$${y}$$を出すブラックボックス」のようなものである。

ここからは、二項関係を用いて関数や写像を定義する。
写像・関数の定義
集合$${X}$$と$${Y}$$において、集合$${X}$$の各要素$${x}$$が集合$${Y}$$のある1つの要素$${y}$$と関係$${R}$$をもつとき、$${R}$$を写像という。この説明は以下のように書くことができる。
$${R \subseteq X \times Y}$$に対して
$${\forall x \in X, \exists y \in Y \space s.t. \space (x,y) \in R}$$
$${\forall x \in X, \space (x,y_1) \in R \land (x,y_2) \in R \to y_1=y_2}$$
の2つを満たす
集合$${X}$$から$${Y}$$への写像における要素の対応について、$${X}$$のすべての要素は$${Y}$$の1つの要素と対応しなければならないが、$${Y}$$には$${X}$$の要素と対応していない要素があってもよい。また、$${X}$$の異なる複数の要素が$${Y}$$のある1つの要素に対応していてもよい。
一般に写像の話をするとき、 $${R}$$の代わりに$${f}$$を用いることとする。
集合$${Y}$$が数の集合のとき、写像$${f}$$を関数という。
※関数について
関数と写像はまったく同じ意味で使われることもあるが、ここでは関数を写像の一部として定義している。
※(おまけ)多価関数について
$${x}$$の値を1つ決めると対応する$${y}$$の値が複数決まるものを多価関数という。この例としては、$${\R ^+}$$における平方根や、様々な複素関数がある。多価関数は関数と付いているが、写像(関数)の定義にあてはまらないため、厳密には関数ではない。
二項関係$${f}$$が写像のとき、写像の要素の対応はふつう$${xfy}$$ではなく、$${f(x)=y}$$または$${f:x\mapsto y}$$と書く。関数において、$${x}$$を独立変数、$${y}$$を従属変数という。
また、写像のもととなる集合の対応は$${f:X \to Y}$$または$${X \xrightarrow{f} Y}$$などと書く。このとき、$${X}$$のことを始域または始集合、$${Y}$$のことを終域または終集合という。
写像$${f:X \to Y}$$があるとき、$${(x,y) \in f}$$となる$${y \in Y}$$が存在するような要素$${x \in X}$$からなる集合を$${f}$$の定義域という。また、終域の部分集合で、$${(x,y) \in f}$$となる$${x \in X}$$が存在するような要素$${y \in Y}$$からなる集合を$${f}$$の値域といい、$${f(X)}$$と表す。定義域と値域を合わせて変域という。写像の定義より定義域は、始域と同じものである。
関数において、定義域が明示されていない場合、定義域は実数のうち関数が定義可能な最大の集合とすればよい。
※値域について
終域と値域はそれぞれ同じ意味で使われていることもあるが、ここでは部分集合として定義している。
写像の例を以下に示す。
$${A=\{1,2,3\},B=\{a,b,c,d,e\}}$$のとき、次のような写像$${f:A \to B}$$を考える。
$${f(1)=a,f(2)=b,f(3)=c}$$
この写像の始域、終域、定義域、値域はそれぞれ以下のようになる。
始域 $${A=\{1,2,3\}}$$
終域 $${B=\{a,b,c,d,e\}}$$
定義域 $${A=\{1,2,3\}}$$
値域 $${f(A)=\{a,b,c\}}$$

写像の分類
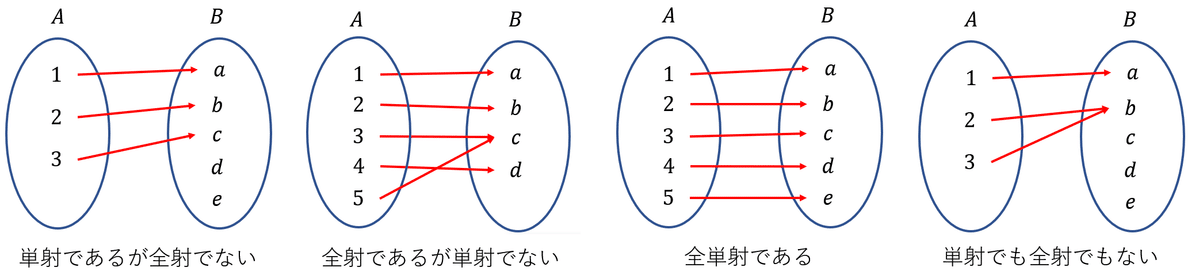
写像$${f:X \to Y}$$について、その分類用語には以下のものがある。
全射(上への写像) $${\forall y \in Y, \exists x \in X \space s.t, \space f(x) = y}$$
単射(1対1の写像) $${\forall x_1, \forall x_2 \in X, x_1 \neq x_2 \Rightarrow f(x_1) \neq f(x_2)}$$または
$${\forall x_1, \forall x_2 \in X, f(x_1)=f(x_2) \Rightarrow x_1=x_2}$$
全単射(上への1対1写像, 1対1対応) 全射かつ単射
単射の2つの定義はそれぞれ対偶となっている。
※写像の分類の考え方
写像$${f:X \to Y}$$について、
・全射
$${Y}$$のすべての要素に、$${X}$$の要素が対応している
・単射
$${X}$$の異なる要素には、$${Y}$$の異なる要素が対応している
・全単射
$${Y}$$のすべての要素に、$${X}$$の異なる要素が対応している
$${X}$$の要素数と$${Y}$$の要素数が等しくなければならない
写像をそれぞれの用語で説明した例を図とともに示す。
合成写像
2つの写像$${f:X \to Y, g:Y \to Z}$$に対して、$${X \xrightarrow{f} Y \xrightarrow{g} Z}$$と写像を対応させたものを合成写像(合成関数)といい、$${(g \circ f)(x)=g(f(x))}$$または
$${g \circ f:X \to Z}$$と表す。
※合成写像$${(g \circ f)(x)}$$はまず、写像$${f}$$を作用させた後に、写像$${g}$$を作用させるので順番に注意する。
写像$${f:A \to B, g:B \to C, h:C \to D}$$に対して、合成写像は結合法則
$${h \circ (g \circ f) = (h \circ g) \circ f}$$が成り立つ。

逆写像
全単射である写像$${f:X \to Y}$$では、$${Y}$$のすべての要素に、$${X}$$の異なる要素が対応している。よって、要素の対応関係を逆にした写像$${f^{-1}:Y \to X}$$を考えることができる。これを逆写像(逆関数)といい、$${f^{-1}(x)}$$とも表す。$${f(x)=y}$$のとき、$${f^{-1}(y)=x}$$となる。もとの写像の定義域は、逆写像の値域に、もとの写像の値域は逆写像の定義域になる。
定義から明らかだが、逆写像の逆写像は元の写像となる。つまり、$${(f^{-1})^{-1}=f}$$である。
全単射である写像$${f:X \to X}$$において、写像とその逆写像の合成写像は、恒等写像(始域と終域が同じで、要素の対応が$${x\mapsto x}$$となる写像)となる。
つまり、$${(f \circ f^{-1})(x) = (f^{-1} \circ f)(x)=x}$$が成り立つ。
写像$${f,g}$$が全単射のとき、合成写像の逆写像は、$${(g \circ f)^{-1}=f^{-1} \circ g^{-1}}$$となる。
部分写像
集合$${X}$$と$${Y}$$において、集合$${X}$$の部分集合$${X'}$$の各要素$${x'}$$が集合$${Y}$$のある1つの要素$${y}$$と関係$${f}$$をもつとき、$${f}$$を部分写像(部分関数)という。部分写像の場合、その定義域は始域の部分集合となる。
部分写像において、特に$${X'=X}$$となるとき、$${f}$$を全域写像(全域関数)という。全域写像は、通常の写像と同じものである。
集合$${X}$$から$${Y}$$への部分写像では、要素の対応について、$${X}$$の要素が$${Y}$$の1つの要素と対応しなければならないが、$${X}$$と$${Y}$$にはそれぞれ相手の要素と対応していない要素があってもよい。
※部分写像は、写像の条件を緩めた概念です。
演習問題7
問題18 写像$${f:\{1,2,3,4\} \to \N, \space f(x)=3x+5}$$について、始域、終域、定義域、値域をそれぞれ求めよ。
[解答]
始域 $${\{1,2,3,4\}}$$
終域 $${\N}$$
定義域 $${\{1,2,3,4\}}$$
値域 $${\{8,11,14,17\}}$$
問題19 $${A=\{0,1,2,3\}, B=\{a,b,c,d\},C=\{\alpha,\beta,\gamma\}}$$とするとき、写像$${f,g}$$をそれぞれ次のように定義する。
$${f:A \to B, f(0)=a,f(1)=b,f(2)=c,f(3)=d}$$
$${g:B \to C, g(a)=\alpha,g(b)=\beta,g(c)=\gamma,g(d)=\alpha}$$
このとき、次の各問に答えよ。
(1) 写像$${f,g}$$について、定義域と値域をそれぞれ求めよ。
(2) 写像$${f,g}$$について、その説明として最も適当なものを(a)~(d)から選べ。
(a)単射であるが、全射でない (b)全射であるが、単射でない
(c)全単射である (d)単射でも全射でもない
(3) 合成写像$${f \circ g, g \circ f}$$をそれぞれ求めよ。ただし、合成写像が定義できない場合は、その理由を答えよ。
(4) 逆写像$${f^{-1}, g^{-1}}$$をそれぞれ求めよ。ただし、逆写像が定義できない場合は、その理由を答えよ。
[解答]
(1)
$${f}$$の定義域 $${\{0,1,2,3\}}$$
$${f}$$の値域 $${\{a,b,c,d\}}$$
$${g}$$の定義域 $${\{a,b,c,d\}}$$
$${g}$$の値域 $${\{\alpha,\beta,\gamma\}}$$
(2)
$${f}$$:(c), $${g}$$:(b)
(3)
写像$${g}$$の終域と写像$${f}$$の始域(定義域)が一致していないので, $${f \circ g}$$は定義できない
$${g \circ f:A \to C}$$
$${(g \circ f)(0)=g(f(0))=g(a)=\alpha}$$
$${(g \circ f)(1)=g(f(1))=g(b)=\beta}$$
$${(g \circ f)(2)=g(f(2))=g(c)=\gamma}$$
$${(g \circ f)(3)=g(f(3))=g(d)=\alpha}$$
(4)
$${f^{-1}:B \to A}$$
$${f^{-1}(a)=0}$$
$${f^{-1}(b)=1}$$
$${f^{-1}(c)=2}$$
$${f^{-1}(d)=3}$$
写像$${g}$$は全単射でないので, $${g^{-1}}$$は定義できない
問題20 $${A=\{1,2,3,…,n\},B=\{1,2,3,…,m\}(n < m)}$$とするとき、次の条件を満たす関数(写像)は全部でいくつあるか。ただし、存在しない場合は0と答えよ。
(1) $${A}$$から$${B}$$への関数(写像)
(2) $${A}$$から$${B}$$への関数(写像)のうち、全射であるもの
(3) $${A}$$から$${B}$$への関数(写像)のうち、単射であるもの
(4) $${A}$$から$${B}$$への関数(写像)のうち、全単射であるもの
(5) $${A}$$から$${A}$$への関数(写像)のうち、全単射であるもの
(6) $${B}$$から$${A}$$への関数(写像)
(7) $${B}$$から$${A}$$への関数(写像)のうち、単射であるもの
(8) $${A}$$から$${B}$$への部分関数(部分写像)
[解答]
(1)
$${A}$$の$${n}$$個の要素それぞれに対して, $${B}$$の$${m}$$個のいずれかの要素と対応していればよいので,
$${m^n}$$
(2)
$${B}$$のすべての要素に$${A}$$の要素が対応していればよく, $${n < m}$$より$${A}$$において$${m-n}$$個の要素が$${B}$$の複数の要素に$${A}$$に対応しなければならない
しかし, これは関数の定義に反するので, 全射は存在しない
よって, 0
(3)
$${A}$$の異なる要素に対応する$${B}$$の要素が異なればよく, $${A}$$のある要素に対応する$${B}$$の要素を1つ決めると, $${A}$$の次の要素は$${B}$$の要素のうち残りの$${m-1}$$個の要素の中から対応する要素を1つ決めなければならない
これを$${A}$$のすべての要素に対して考えるので,
$${m \times (m-1) \times (m-2) \times … \times (m-n+1)= \dfrac{m!}{(m-n)!}}$$
(4)
$${B}$$のすべての要素に$${A}$$の異なる要素が対応していればよく, $${n < m}$$より全単射は存在しない
よって, 0
(5)
終域$${A}$$のすべての要素に始域$${A}$$の異なる要素が対応していればよく, 終域$${A}$$のある要素に対応する始域$${A}$$の要素を1つ決めると, 終域$${A}$$の次の要素は始域$${A}$$の要素のうち残りの$${n-1}$$個の要素の中から対応する要素を1つ決めなければならない
これを終域$${A}$$のすべての要素に対して考えるので,
$${n!}$$
(6)
$${B}$$の$${m}$$個の要素それぞれに対して, $${A}$$の$${n}$$個のいずれかの要素と対応していればよいので,
$${n^m}$$
(7)
$${B}$$の異なる要素に対応する$${A}$$の要素が異なればよく, $${n < m}$$より(鳩の巣原理より)単射は存在しない
よって, 0
(8)
$${A}$$の$${n}$$個の要素それぞれに対して, $${B}$$の$${m}$$個のいずれかの要素と対応するか, どの要素とも対応しない(未定義)かであればよいので,
$${(m+1)^n}$$
※(7)の解答に書いた鳩の巣原理とは、$${n < m}$$のとき$${n}$$個の巣に$${m}$$羽の鳩が入るとき、少なくとも1個の巣には2羽以上の鳩が入っているという原理である。直観的に理解できる原理である。
最後に
今回は、大学数学・集合論の解説記事として、写像・関数について解説しました。今回の内容は、微積分(解析学)にも関連しています。次回は、有限集合と無限集合の解説記事となる予定です。では。
この記事の続きは以下の記事です。
