
【線形代数】4 行列の簡約化とランク
こんにちは、これが394本目の記事となったすうじょうです。今日は、大学数学の解説記事です。今回の内容は、線形代数より行列の簡約化とランクを解説します。
この記事は、以下の記事の続きです。
行列の基本変形
行列の基本変形の重要性
行列の基本変形は、線形代数において重要な変形である。後で取り扱う連立1次方程式、逆行列、行列式を求めるときに利用する。このため、ミスなく行列を目的の形にするために、基本変形を選択し計算できるようになる必要がある。
行列の行基本変形
行列の行について行う以下の3つの変形を行基本変形または左基本変形という。
(1) 2つの行を入れ替える
$${i}$$行目と$${j}$$行目を入れ替える($${i\neq j}$$)
(2) ある行に0でない数をかける
$${i}$$行目を$${c}$$倍する($${c\neq 0}$$)
(3) ある行に他の行を何倍かしたものを足す
$${i}$$行目に$${j}$$行目の$${c}$$倍を足す($${i\neq j, c\neq 0}$$)
以降それぞれ$${(1)\textcircled{i}\leftrightarrow\textcircled{j},(2)\textcircled{i}\times c, (3)\textcircled{i}+\textcircled{j}\times c}$$と略記する。
行基本変形は可逆な変形である。つまり、行った変形を戻すような逆の変形を行えば元の行列に戻すことができる。
$${m\times n}$$の行列に対して行基本変形を行った結果は、$${m}$$次単位行列$${I_m}$$に対して同じ変形を行った基本行列を左からかけた積と同じ結果となる。このことから、左基本変形ともいう。
$${m}$$次単位行列$${I_m}$$に対して、
$${\textcircled{i}\leftrightarrow\textcircled{j}}$$を行った行列を$${P_m(i,j)}$$と表す。
$${\textcircled{i}\times c}$$を行った行列を$${Q_m(i;c)}$$と表す。
$${\textcircled{i}+\textcircled{j}\times c}$$を行った行列を$${R_m(i,j;c)}$$と表す。
以下に行基本変形の例を示す。
$$
\begin{aligned}
&A=\begin{pmatrix}
a & b\\
c & d\\
e & f
\end{pmatrix}
に対して\\
&\textcircled{1}\leftrightarrow\textcircled{3}\\
&P_3(1,3)A=\begin{pmatrix}
0 & 0 & 1\\
0 & 1 & 0\\
1 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
a & b\\
c & d\\
e & f
\end{pmatrix}
=\begin{pmatrix}
e & f\\
c & d\\
a & b
\end{pmatrix}\\
&\textcircled{2}\times 3\\
&Q_3(2;3)A=\begin{pmatrix}
1 & 0 & 0\\
0 & 3 & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
a & b\\
c & d\\
e & f
\end{pmatrix}
=\begin{pmatrix}
a & b\\
3c & 3d\\
e & f
\end{pmatrix}\\
&\textcircled{1}+\textcircled{2}\times 2\\
&R_3(1,2;2)A=\begin{pmatrix}
1 & 2 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
a & b\\
c & d\\
e & f
\end{pmatrix}
=\begin{pmatrix}
a+2c & b+2d\\
c & d\\
e & f
\end{pmatrix}
\end{aligned}
$$
行列の列基本変形
行列の列について行う以下の3つの変形を列基本変形または右基本変形という。
(1) 2つの列を入れ替える
$${i}$$列目と$${j}$$列目を入れ替える($${i\neq j}$$)
(2) ある列に0でない数をかける
$${i}$$列目を$${c}$$倍する($${c\neq 0}$$)
(3) ある列に他の列を何倍かしたものを足す
$${i}$$列目に$${j}$$列目の$${c}$$倍を足す($${i\neq j, c\neq 0}$$)
以降それぞれ$${(1)\boxed{i}\leftrightarrow\boxed{j},(2)\boxed{i}\times c, (3)\boxed{i}+\boxed{j}\times c}$$と略記する。
列基本変形は可逆な変形である。つまり、行った変形を戻すような逆の変形を行えば元の行列に戻すことができる。
$${m\times n}$$の行列に対して行基本変形を行った結果は、$${n}$$次単位行列$${I_n}$$に対して同じ変形を行った基本行列を右からかけた積と同じ結果となる。このことから、右基本変形ともいう。
$${n}$$次単位行列$${I_n}$$に対して、
$${\boxed{i}\leftrightarrow\boxed{j}}$$を行った行列を$${P_m(i,j)}$$と表す。
$${\boxed{i}\times c}$$を行った行列を$${Q_m(i;c)}$$と表す。
$${\boxed{i}+\boxed{j}\times c}$$を行った行列を$${R_m(j,i;c)}$$と表す。
※この基本行列は、行基本変形のときと同じ概念である。ただし、(3)の変形と基本行列の添え字の対応は$${i,j}$$が逆になっていることに注意する。
以下に列基本変形の例を示す。
$$
\begin{aligned}
&A=\begin{pmatrix}
a & b\\
c & d\\
e & f
\end{pmatrix}
に対して\\
&\boxed{1}\leftrightarrow\boxed{2}\\
&AP_2(1,2)=\begin{pmatrix}
a & b\\
c & d\\
e & f
\end{pmatrix}
\begin{pmatrix}
0 & 1\\
1 & 0
\end{pmatrix}
=\begin{pmatrix}
b & a\\
d & c\\
f & e
\end{pmatrix}\\
&\boxed{1}\times 2\\
&AQ_2(1;2)=\begin{pmatrix}
a & b\\
c & d\\
e & f
\end{pmatrix}
\begin{pmatrix}
2 & 0\\
0 & 1
\end{pmatrix}
=\begin{pmatrix}
2a & b\\
2c & d\\
2e & f
\end{pmatrix}\\
&\boxed{1}+\boxed{2}\times 4\\
&AR_2(2,1;4)=\begin{pmatrix}
a & b\\
c & d\\
e & f
\end{pmatrix}
\begin{pmatrix}
1 & 0\\
4 & 1
\end{pmatrix}
=\begin{pmatrix}
a+4b & b\\
c+4d & d\\
e+4f & f
\end{pmatrix}
\end{aligned}
$$
基本行列の補足
基本行列について、以下のことがいえる。
$${P_m(i,j)P_m(i,j)=I_m,\\Q_m(i;c)Q_m(i;\dfrac{1}{c})=Q_m(i;\dfrac{1}{c})Q_m(i;c)=I_m,\\R_m(i,j;c)R(i,j;-c)=R(i,j;-c)R_m(i,j;c)=I_m}$$
よって、基本行列は正則で、その逆行列はそれぞれ以下のようになる。
$${P_m(i,j)^{-1}=P_m(i,j),Q_m(i;c)^{-1}=Q_m(i;\dfrac{1}{c}),R_m(i,j;c)^{-1}=R(i,j;-c)}$$
基本変形の逆の変形は、それぞれの逆行列である基本行列が意味する変形に対応している。(行基本変形なら左から、列基本変形なら右から逆行列をかける)
行列の簡約化
階段行列とランク
$${m \times n}$$の行列が以下の形のとき、階段行列という。
$$
\begin{pmatrix}
& & d_1 & * & \cdots & \cdots & \cdots & \cdots & \cdots\\
& & & & d_2 & * & \cdots & \cdots & \cdots\\
& & & & & \ddots & \ddots & \vdots &\vdots \\
\LARGE O& & & & & & d_r & * & \cdots\\
\\
\end{pmatrix}
$$
ただし、$${0 \leq r \leq m, d_i\neq 0(1\leq i \leq r), * \in \R}$$とする。
※行列の要素の一部にどんな値が入ってもいい場合、成分の代わりに*が書かれていることが多い。
行列において、各行の最も左にある0でない数を主成分という。
$${m \times n}$$の階段行列$${A}$$において最も下の主成分が$${d_r}$$($${r}$$行目)のとき、$${r}$$を階段行列のランクまたは階数といい、$${\text{rank}A=r}$$と表す。
また、$${n}$$次正方行列において、$${\text{rank}A < n}$$のとき$${A}$$をランク落ちした行列という。$${\text{rank}A = n}$$のときフルランクという。
※ランクは、階段行列の0以外の成分を階段とみたときの段数となっている。
階段行列とそのランクの例を以下に示す。

ただし、以下の例のような行列は階段行列ではない。
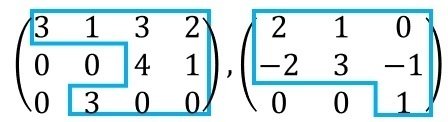
左の行列は、階段の形になっていない。右の行列は、階段の1段が1行になっていない。
簡約行列
$${m \times n}$$の行列が以下の形のとき、簡約行列(簡約階段行列)という。
$$
\begin{pmatrix}
& & 1 & * & \cdots & 0 &* & \cdots & 0 & *& \cdots\\
& & & & &1 & * & \cdots & 0 & *& \cdots\\
& & & & & & & \ddots & \vdots & &\\
\LARGE O & & & & & & & & 1 & * & \cdots \\
\\
\end{pmatrix}
$$
ただし、$${* \in \R}$$とする。
※簡約行列は、階段行列に主成分$${d_i=1}$$と主成分$${1}$$のある列は基本列ベクトルとなる(主成分以外の成分は0)という制約を加えた行列である。つまり、簡約行列は階段行列の特別な場合である。
行列の簡約化
任意の行列は、行基本変形を繰り返すことで簡約行列に変形できる。この変形のことを行列の簡約化という。また、簡約化する変形の繰り返しは何通りもあるが、簡約行列は唯一つに定まる。
具体的には、以下の手順で簡約化する。
[1] 1行目以下の成分のうち、最も左にある0でない数を探し、その列を第$${n_1}$$列とする
[2] 行列の$${(1,n_1)}$$成分が$${1}$$となるように行基本変形を行う
[2-1] 第$${n_1}$$列で1行目以下の中に$${1,-1}$$がある場合は、行を入れ替える
[2-2] 第$${n_1}$$列で1行目以下の成分に互いに素な数のペア$${a,b}$$がある場合は、$${ax+by=1,-1}$$を満たす整数$${x,y}$$を見つけ、$${1,-1}$$を作り、行を入れ替える
[2-3] 第$${n_1}$$列で1行目以下の成分に$${1}$$がない場合、第1行を何倍かして$${1}$$にする
[3] $${(1,n_1)}$$成分の$${1}$$の何倍かを他の行に足すことで、第$${n_1}$$列の1行目以外の成分を0にする(基本ベクトルにする)
[4] 2行目から最後の行まで、すべての行に対して、[1]~[3]を同様に行う
※[2-2]について、行基本変形の回数を少なくするために、$${x=1}$$または$${y = 1}$$となる組み合わせを優先的に探す。
※[2-1]~[2-3]について、計算の途中でできるだけ分数を作らないようにし、計算ミスを減らす工夫をしている。
この変形を行列で表すと、行列$${A}$$に、基本行列$${E_1,E_2,…,E_k}$$を順に左からかけて簡約行列にしている。つまり、$${EA=E_k \cdots E_2E_1A}$$が簡約行列である。また、基本行列は正則であるので、$${E}$$は正則である。
簡約行列にする手順のことを、掃き出し法またはガウスの消去法という。また、手順[3]の操作を$${(1,n_1)}$$成分で第$${n_1}$$列を掃き出すという。
$${m \times n}$$の行列$${A}$$を簡約化した行列のランクを行列$${A}$$のランクといい、$${\text{rank}A}$$と表す。ただし、ランクを求めるだけであれば、簡約化までせずに階段行列にするだけで求めることができる。
行列の簡約化の例を以下に示す。
$$
\begin{pmatrix}
2 & 3 & 1\\
1 & -1 & 4
\end{pmatrix}
\overset{\textcircled{1}\leftrightarrow\textcircled{2}}{\longrightarrow}
\begin{pmatrix}
1 & -1 & 4\\
2 & 3 & 1
\end{pmatrix}
\overset{\textcircled{2}+\textcircled{1}\times (-2)}{\longrightarrow}
\begin{pmatrix}
1 & -1 & 4\\
0 & 5 & -7
\end{pmatrix}
\\
\overset{\textcircled{2}\times \dfrac{1}{5}}{\longrightarrow}
\begin{pmatrix}
1 & -1 & 4\\
0 & 1 & -\dfrac{7}{5}
\end{pmatrix}
\overset{\textcircled{1}+\textcircled{2}\times 1}{\longrightarrow}
\begin{pmatrix}
1 & 0 & \dfrac{13}{5}\\
0 & 1 & -\dfrac{7}{5}
\end{pmatrix}
$$
行列の階数標準形
この内容は重要度が低いので、飛ばしてもらっても構わない。
任意の行列を行基本変形のみによって簡約行列に変形した。これにさらに列基本変形を繰り返すことで行列の階数標準形(あるいは単に標準形)に変形できる。また、行列の階数標準形は唯一つに定まる。
行列のランクが$${r}$$のとき、行列の階数標準形は以下の形となる。
$$
\begin{pmatrix}
I_r & \large O\\
\large O & \large O
\end{pmatrix}
$$
具体的には、簡約行列の主成分1を用いて、何倍かを足す列基本変形で階数標準形にする。
行列の簡約化の例で求めた簡約行列を、階数標準形にする変形を以下に示す。
$$
\begin{pmatrix}
1 & 0 & \dfrac{13}{5}\\
0 & 1 & -\dfrac{7}{5}
\end{pmatrix}
\overset{\boxed{3}+\boxed{1}\times (-\dfrac{13}{5})}{\overset{\boxed{3}+\boxed{2}\times \dfrac{7}{5}}{\longrightarrow}}
\begin{pmatrix}
1 & 0 & 0\\
0 & 1 & 0
\end{pmatrix}
$$
演習問題4
問題7 次の行列に対して、簡約行列とランクを求めよ。
$$
\begin{aligned}
&(1)\begin{pmatrix}
1&1&-1\\
2&0&1\\
-1&1&0
\end{pmatrix}
(2)\begin{pmatrix}
2&1&3\\
3&-1&4\\
1&2&-2
\end{pmatrix}
(3)\begin{pmatrix}
5&-2&3&1\\
3&4&-5&5\\
2&3&1&6
\end{pmatrix}\\
&(4)\begin{pmatrix}
1&0&2&-3\\
0&1&2&5\\
2&0&3&1\\
1&1&4&2
\end{pmatrix}
(5)\begin{pmatrix}
1&-1&2&1&3\\
2&-1&1&2&2\\
-1&1&2&3&5\\
0&1&-1&2&4
\end{pmatrix}
\end{aligned}
$$
[方針]
解答で行っている行基本変形はあくまで一例である。ただし、どのような変形をしても簡約行列は一致する。
[解答]
$$
\begin{aligned}
&(1)\\
&\begin{pmatrix}
1&1&-1\\
2&0&1\\
-1&1&0
\end{pmatrix}
\overset{\textcircled{2}+\textcircled{1}\times (-2)}{\overset{\textcircled{3}+\textcircled{1}\times 1}{\longrightarrow}}
\begin{pmatrix}
1&1&-1\\
0&-2&3\\
0&2&-1
\end{pmatrix}
\overset{\textcircled{2}\times (-\dfrac{1}{2})}{\longrightarrow}
\begin{pmatrix}
1&1&-1\\
0&1&-\dfrac{3}{2}\\
0&2&-1
\end{pmatrix}\\
&\overset{\textcircled{1}+\textcircled{2}\times (-1)}{\overset{\textcircled{3}+\textcircled{2}\times (-2)}{\longrightarrow}}
\begin{pmatrix}
1&0&\dfrac{1}{2}\\
0&1&-\dfrac{3}{2}\\
0&0&2
\end{pmatrix}
\overset{\textcircled{3}\times \dfrac{1}{2}}{\longrightarrow}
\begin{pmatrix}
1&0&\dfrac{1}{2}\\
0&1&-\dfrac{3}{2}\\
0&0&1
\end{pmatrix}
\overset{\textcircled{1}+\textcircled{3}\times (-\dfrac{1}{2})}{\overset{\textcircled{3}+\textcircled{2}\times \dfrac{3}{2}}{\longrightarrow}}
\begin{pmatrix}
1&0&0\\
0&1&0\\
0&0&1
\end{pmatrix}\\
&ランク 3
\end{aligned}
$$
$$
\begin{aligned}
&(2)\\
&\begin{pmatrix}
2&1&3\\
3&-1&4\\
1&2&-2
\end{pmatrix}
\overset{\textcircled{1}\leftrightarrow\textcircled{3}}{\longrightarrow}
\begin{pmatrix}
1&2&-2\\
2&1&3\\
3&-1&4
\end{pmatrix}
\overset{\textcircled{2}+\textcircled{1}\times (-2)}{\overset{\textcircled{3}+\textcircled{1}\times (-3)}{\longrightarrow}}
\begin{pmatrix}
1&2&-2\\
0&-3&7\\
0&-7&10
\end{pmatrix}\\
&\overset{\textcircled{3}+\textcircled{2}\times (-2)}{\longrightarrow}
\begin{pmatrix}
1&2&-2\\
0&-3&7\\
0&-1&-4
\end{pmatrix}
\overset{\textcircled{3}\times (-1)}{\longrightarrow}
\begin{pmatrix}
1&2&-2\\
0&-3&7\\
0&1&4
\end{pmatrix}
\overset{\textcircled{2}\leftrightarrow\textcircled{3}}{\longrightarrow}
\begin{pmatrix}
1&2&-2\\
0&1&4\\
0&-3&7
\end{pmatrix}\\
&\overset{\textcircled{1}+\textcircled{2}\times (-2)}{\overset{\textcircled{3}+\textcircled{2}\times 3}{\longrightarrow}}
\begin{pmatrix}
1&0&-10\\
0&1&4\\
0&0&19
\end{pmatrix}
\overset{\textcircled{3}\times \dfrac{1}{19}}{\longrightarrow}
\begin{pmatrix}
1&0&-10\\
0&1&4\\
0&0&1
\end{pmatrix}
\overset{\textcircled{1}+\textcircled{3}\times 10}{\overset{\textcircled{2}+\textcircled{3}\times (-4)}{\longrightarrow}}
\begin{pmatrix}
1&0&0\\
0&1&0\\
0&0&1
\end{pmatrix}\\
&ランク 3
\end{aligned}
$$
※$${\overset{\textcircled{3}+\textcircled{2}\times (-2)}{\longrightarrow}}$$について、第2列で2行目以下の成分に互いに素な数のペア$${-3,-7}$$があるので、$${-3x-7y=1,-1}$$を満たす整数$${x,y}$$を探す。$${-3}$$の倍数$${…,9,6,3,-3,-6,-9,…}$$と$${-7}$$の倍数$${…,21,14,7,-7,-14,-21,…}$$の中で足すと$${1,-1}$$になる組み合わせを探すと、$${-3(-2)-7(1)=6-7=-1}$$が見つかる。
$$
\begin{aligned}
&(3)\\
&\begin{pmatrix}
5&-2&3&1\\
3&4&-5&5\\
2&3&1&6
\end{pmatrix}
\overset{\textcircled{2}+\textcircled{3}\times (-1)}{\longrightarrow}
\begin{pmatrix}
5&-2&3&1\\
1&1&-6&1\\
2&3&1&6
\end{pmatrix}\\
&\overset{\textcircled{1}\leftrightarrow\textcircled{2}}{\longrightarrow}
\begin{pmatrix}
1&1&-6&1\\
5&-2&3&1\\
2&3&1&6
\end{pmatrix}
\overset{\textcircled{2}+\textcircled{1}\times (-5)}{\overset{\textcircled{3}+\textcircled{1}\times (-2)}{\longrightarrow}}
\begin{pmatrix}
1&1&-6&1\\
0&-7&33&6\\
0&1&13&8
\end{pmatrix}\\
&\overset{\textcircled{2}\leftrightarrow\textcircled{3}}{\longrightarrow}
\begin{pmatrix}
1&1&-6&-1\\
0&1&13&8\\
0&-7&33&6
\end{pmatrix}
\overset{\textcircled{1}+\textcircled{2}\times (-1)}{\overset{\textcircled{3}+\textcircled{2}\times 7}{\longrightarrow}}
\begin{pmatrix}
1&0&-19&-9\\
0&1&13&8\\
0&0&124&62
\end{pmatrix}\\
&\overset{\textcircled{3}\times \dfrac{1}{124}}{\longrightarrow}
\begin{pmatrix}
1&0&-19&-9\\
0&1&13&8\\
0&0&1&\dfrac{1}{2}
\end{pmatrix}
\overset{\textcircled{1}+\textcircled{3}\times 19}{\overset{\textcircled{2}+\textcircled{3}\times (-13)}{\longrightarrow}}
\begin{pmatrix}
1&0&0&\dfrac{1}{2}\\
0&1&0&\dfrac{3}{2}\\
0&0&1&\dfrac{1}{2}
\end{pmatrix}\\
&ランク3
\end{aligned}
$$
※$${\overset{\textcircled{2}+\textcircled{3}\times (-1)}{\longrightarrow}}$$について、第1列で1行目以下の成分に互いに素な数のペア$${3,2}$$があるので、$${3x+2y=1,-1}$$を満たす整数$${x,y}$$を探す。$${3}$$の倍数$${…,-9,-6,-3,3,6,9,…}$$と$${2}$$の倍数$${…,-6,-4,-2,2,4,6,…}$$の中で足すと$${1,-1}$$になる組み合わせを探すと、$${3(1)+2(-1)=3-2=1}$$が見つかる。今回の場合、互いに素な数のペアは他にもあり、それを用いて変形してもよい。
$$
\begin{aligned}
&(4)\\
&\begin{pmatrix}
1&0&2&-3\\
0&1&2&5\\
2&0&3&1\\
1&1&4&2
\end{pmatrix}
\overset{\textcircled{3}+\textcircled{1}\times (-2)}{\overset{\textcircled{4}+\textcircled{1}\times (-1)}{\longrightarrow}}
\begin{pmatrix}
1&0&2&-3\\
0&1&2&5\\
0&0&-1&7\\
0&1&2&5
\end{pmatrix}\\
&\overset{\textcircled{4}+\textcircled{2}\times (-1)}{\longrightarrow}
\begin{pmatrix}
1&0&2&-3\\
0&1&2&5\\
0&0&-1&7\\
0&0&0&0
\end{pmatrix}
\overset{\textcircled{3} \times (-1)}{\longrightarrow}
\begin{pmatrix}
1&0&2&-3\\
0&1&2&5\\
0&0&1&-7\\
0&0&0&0
\end{pmatrix}\\
&\overset{\textcircled{1}+\textcircled{3}\times (-2)}{\overset{\textcircled{2}+\textcircled{3}\times (-2)}{\longrightarrow}}
\begin{pmatrix}
1&0&0&11\\
0&1&0&19\\
0&0&1&-7\\
0&0&0&0
\end{pmatrix}\\
&ランク3
\end{aligned}
$$
$$
\begin{aligned}
&(5)\\
&\begin{pmatrix}
1&-1&2&1&3\\
2&-1&1&2&2\\
-1&1&2&3&5\\
0&1&-1&2&4
\end{pmatrix}
\overset{\textcircled{2}+\textcircled{1}\times (-2)}{\overset{\textcircled{3}+\textcircled{1}\times 1}{\longrightarrow}}
\begin{pmatrix}
1&-1&2&1&3\\
0&1&-3&0&-4\\
0&0&4&4&8\\
0&1&-1&2&4
\end{pmatrix}\\
&\overset{\textcircled{1}+\textcircled{2}\times 1}{\overset{\textcircled{4}+\textcircled{2}\times (-1)}{\longrightarrow}}
\begin{pmatrix}
1&0&-1&1&-1\\
0&1&-3&0&-4\\
0&0&4&4&8\\
0&0&2&2&8
\end{pmatrix}
\overset{\textcircled{3}\times \dfrac{1}{4}}{\longrightarrow}
\begin{pmatrix}
1&0&-1&1&-1\\
0&1&-3&0&-4\\
0&0&1&1&2\\
0&0&2&2&8
\end{pmatrix}\\
&\overset{\textcircled{1}+\textcircled{3}\times 1}{\overset{\textcircled{2}+\textcircled{3}\times 3}{\overset{\textcircled{4}+\textcircled{3}\times (-2)}{\longrightarrow}}}
\begin{pmatrix}
1&0&0&2&1\\
0&1&0&3&2\\
0&0&1&1&2\\
0&0&0&0&4
\end{pmatrix}
\overset{\textcircled{3}\times \dfrac{1}{4}}{\longrightarrow}
\begin{pmatrix}
1&0&0&2&1\\
0&1&0&3&2\\
0&0&1&1&2\\
0&0&0&0&1
\end{pmatrix}\\
&\overset{\textcircled{1}+\textcircled{4}\times (-1)}{\overset{\textcircled{2}+\textcircled{4}\times (-2)}{\overset{\textcircled{3}+\textcircled{4}\times (-2)}{\longrightarrow}}}
\begin{pmatrix}
1&0&0&2&0\\
0&1&0&3&0\\
0&0&1&1&0\\
0&0&0&0&1
\end{pmatrix}\\
&ランク4
\end{aligned}
$$
問題8 次の行列のランクを求めよ。
$$
\begin{pmatrix}
a&1&1\\
1&a&1\\
1&1&a
\end{pmatrix}
(aは定数)
$$
[方針]
$${a}$$の値によって、ランクが異なるので場合分けをする。
[解答]
$$
\begin{aligned}
&\begin{pmatrix}
a&1&1\\
1&a&1\\
1&1&a
\end{pmatrix}
\overset{\textcircled{1}\leftrightarrow\textcircled{3}}{\longrightarrow}
\begin{pmatrix}
1&1&a\\
1&a&1\\
a&1&1
\end{pmatrix}
\overset{\textcircled{2}+\textcircled{1}\times (-1)}{\overset{\textcircled{3}+\textcircled{1}\times (-a)}{\longrightarrow}}
\begin{pmatrix}
1&1&a\\
0&a-1&1-a\\
0&1-a&1-a^2
\end{pmatrix}\\
&(\text{i})a=1のとき\\
&\begin{pmatrix}
1&1&1\\
0&0&0\\
0&0&0
\end{pmatrix}
ランク1\\
&(\text{ii})a\neq 1のとき\\
&\begin{pmatrix}
1&1&a\\
0&a-1&1-a\\
0&1-a&1-a^2
\end{pmatrix}
\overset{\textcircled{2}\times \frac{1}{a-1}}{\overset{\textcircled{3}\times \frac{1}{1-a}}{\longrightarrow}}
\begin{pmatrix}
1&1&a\\
0&1&-1\\
0&1&1+a
\end{pmatrix}
\overset{\textcircled{1}+\textcircled{2}\times (-1)}{\overset{\textcircled{3}+\textcircled{2}\times (-1)}{\longrightarrow}}
\begin{pmatrix}
1&0&a+1\\
0&1&-1\\
0&0&2+a
\end{pmatrix}\\
&2+a=0\therefore a=-2のとき ランク2, a \neq -2のとき ランク3\\
&(\text{i}),(\text{ii})より\\
&a=1のときランク1, a=-2のときランク2, a \neq -2,1のときランク3\\
\end{aligned}
$$
問題9 行列$${A}$$が次のように定義されるとき、$${EA}$$が簡約行列となるような行列$${E}$$を求めよ。
$$
A=\begin{pmatrix}
1&1&-2\\
1&1&-1\\
-2&-3&4
\end{pmatrix}
$$
[方針]
行列の簡約化は、行基本変形に対応する基本行列を順に左からかけていった積に等しい。
[解答]
$$
\begin{aligned}
&\begin{pmatrix}
1&1&-2\\
1&1&-1\\
-2&-3&4
\end{pmatrix}
\overset{(1)\textcircled{2}+\textcircled{1}\times (-1)}{\overset{(2)\textcircled{3}+\textcircled{1}\times 2}{\longrightarrow}}
\begin{pmatrix}
1&1&-2\\
0&0&1\\
0&-1&0
\end{pmatrix}
\overset{(3)\textcircled{2}\leftrightarrow\textcircled{3}}{\longrightarrow}
\begin{pmatrix}
1&1&-2\\
0&-1&0\\
0&0&1
\end{pmatrix}\\
&\overset{(4)\textcircled{2}\times (-1)}{\longrightarrow}
\begin{pmatrix}
1&1&-2\\
0&1&0\\
0&0&1
\end{pmatrix}
\overset{(5)\textcircled{1}+\textcircled{2}\times (-1)}{\longrightarrow}
\begin{pmatrix}
1&0&-2\\
0&1&0\\
0&0&1
\end{pmatrix}
\overset{(6)\textcircled{1}+\textcircled{3}\times 2}{\longrightarrow}
\begin{pmatrix}
1&0&0\\
0&1&0\\
0&0&1
\end{pmatrix}\\
&(1)\text{\textasciitilde}(6)の基本変形に対応する基本行列は以下のようになる\\
&(1):R_3(2,1;-1)=\begin{pmatrix}
1&0&0\\
-1&1&0\\
0&0&1
\end{pmatrix}
(2):R_3(3,1;2)=\begin{pmatrix}
1&0&0\\
0&1&0\\
2&0&1
\end{pmatrix}\\
&(3):P_3(2,3)=\begin{pmatrix}
1&0&0\\
0&0&1\\
0&1&0
\end{pmatrix}
(4):Q_3(2;-1)=\begin{pmatrix}
1&0&0\\
0&-1&0\\
0&0&1
\end{pmatrix}\\
&(5):R_3(1,2;-1)=\begin{pmatrix}
1&-1&0\\
0&1&0\\
0&0&1
\end{pmatrix}
(6):R_3(1,3;2)=\begin{pmatrix}
1&0&2\\
0&1&0\\
0&0&1
\end{pmatrix}\\
&よって\\
&E=R_3(1,3;2)R_3(1,2;-1)Q_3(2;-1)P_3(2,3)R_3(3,1;2)R_3(2,1;-1)\\
&\hspace{0.8em}=\begin{pmatrix}
1&2&1\\
-2&0&-1\\
-1&1&0
\end{pmatrix}
\end{aligned}
$$
※$${E}$$が正しいかどうかは、$${EA}$$を計算して求めた簡易行列と一致するかどうか確認すればよい。
最後に
今回は、大学数学・線形代数の解説記事として、行列の簡約化とランクを解説しました。今回の内容は、線形代数において重要な変形である基本変形を含んでいます。次回は、連立1次方程式の解法の解説記事となる予定です。では。
この記事の続きは以下の記事です。
