
【線形代数】2 行列の基礎とその演算
こんにちは、これが381本目の記事となったすうじょうです。今日は、大学数学の解説記事です。今回の内容は、線形代数より行列の基礎を解説します。
この記事は、以下の記事の続きです。
行列とは
行列とその用語
数を長方形上に並べたものを行列という。行列は、例えば
$$
A_1=\begin{pmatrix}
1 \\
2
\end{pmatrix}
,
A_2=\begin{pmatrix}
1 & 2 & 3
\end{pmatrix}
,
A_3=\begin{pmatrix}
1 & -2 & 3 \\
10 & 6 & 0
\end{pmatrix}
,
A_4=\begin{pmatrix}
4 & 9 \\
1 & 7
\end{pmatrix}
$$
のように書く。このように、行列はベクトルと異なり、アルファベット大文字で表されることが多い。(太字の場合もある)
成分がすべて実数である行列を実行列、成分がすべて複素数である行列を複素行列ということがある。
一般の行列$${A}$$を用いて、行列の用語を説明する。
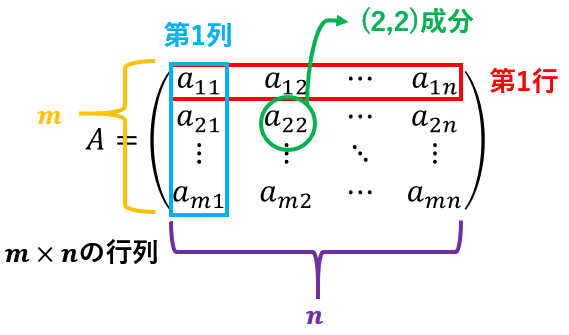
行列の$${a_{11},a_{m2}}$$などの数を成分または要素という。横の数字の並びを行、縦の数字の並びを列という。「横、縦」の順で、行・列と覚えてもよい。
具体的に、$${a_{11} a_{12} \cdots a_{1n}}$$の横の並びを行列の上から1番目の行であることから、第1行または1行といい、$${a_{m1} a_{m2} \cdots a_{mn}}$$の横の並びを行列の上から$${m}$$番目の行であることから、第$${m}$$行または$${m}$$行という。
同じように、$${a_{11} a_{21} \cdots a_{m1}}$$の縦の並びを行列の左から1番目の列であることから、第1列または1列といい、$${a_{1n} a_{2n} \cdots a_{mn}}$$の縦の並びを行列の左から$${n}$$番目の列であることから、第$${n}$$列または$${n}$$列という。
第$${i}$$行と第$${j}$$列の交点にある成分を行列の$${(i,j)}$$成分といい、$${a_{ij}}$$と表す。
また、行列のサイズについて、$${m}$$個の行、$${n}$$個の列からなる行列を$${m\times n}$$の行列、$${(m,n)}$$型行列、$${m}$$行$${n}$$列の行列などという。
行列をその$${(i,j)}$$成分を用いて、$${A=(a_{ij}),B=(b_{ij})}$$などと表すことがある。
$${n\times n}$$の行列は、数が正方形状に並んでいるので$${n}$$次正方行列という。$${n}$$次正方行列において、$${a_{11} a_{22} \cdots a_{nn}}$$の左上から右下の並びを対角成分という。$${n}$$次正方行列$${A}$$において、対角成分の和を行列のトレースといい、$${\text{tr}(A)=a_{11}+a_{22}+…+a_{nn}}$$と表す。
$${m\times 1}$$の行列は、$${m}$$次元列ベクトルといい、$${1\times n}$$の行列は、$${n}$$次元行ベクトルという。つまり、ベクトルは行列の特別な場合と考えることができる。
上の行列$${A_1,A_2,A_3,A_4}$$のうち、$${A_1}$$は2次元列ベクトル、$${A_2}$$は3次元行ベクトル、$${A_3}$$は$${2\times 3}$$の行列、$${A_4}$$は2次正方行列である。
※$${1\times1}$$の行列は、ふつう数とみなす。
すべての成分が0の行列を零行列といい、$${O}$$または$${O_{mn}}$$と表す。また、すべての成分が0のベクトルを零ベクトルといい、$${\bm{0}}$$と表す。
$${n}$$次正方行列($${n\times n}$$の行列)$${A=(a_{ij})}$$で、対角成分以外の成分がすべて0である($${i \neq j}$$に対して$${a_{ij}=0}$$)行列を対角行列といい、$${\text{diag}(a_{11},a_{22},\cdots ,a_{nn})}$$と表す。特に、対角成分がすべて1である対角行列を単位行列といい、$${I_n,E_n,I,E}$$と表す。ここでは、$${I_n,I}$$を単位行列とする。
単位行列の成分を、
$$
\delta_{iJ}=\begin{cases}
1 &(i =j) \\
0 &(i \neq j)
\end{cases}
$$
と表すこともあり、$${\delta_{ij}}$$をクロネッカーのデルタという。これを用いて、単位行列を$${I=(\delta_{ij})}$$と表すことができる。
対角行列と単位行列の成分は以下のようになる。
$$
\text{diag}(a_{11},a_{22},\cdots ,a_{nn})=\begin{pmatrix}
a_{11}& & &\LARGE{O}\\
&a_{22}& &\\
& &\ddots& \\
\LARGE{O}& & & a_{nn}
\end{pmatrix}
,
I=\begin{pmatrix}
1& &\LARGE{O}\\
&\ddots& \\
\LARGE{O}& &1
\end{pmatrix}
$$
※成分中の大きな零行列はそのスペースの成分がすべて0であることを表す。
対角行列と単位行列の例を以下に示す。
$$
\text{diag}(2,3,-1,4)=\begin{pmatrix}
2&0&0& 0\\
0&3& 0&0\\
0&0&-1&0\\
0&0&0&4
\end{pmatrix}
,
I_3=\begin{pmatrix}
1&0&0\\
0&1& 0\\
0&0&1
\end{pmatrix}
$$
$${n}$$次正方行列($${n\times n}$$の行列)$${A=(a_{ij})}$$で、対角成分より下の成分がすべて0である($${i > j}$$に対して$${a_{ij}=0}$$)行列を上三角行列という。また、対角成分より上の成分がすべて0である($${i < j}$$に対して$${a_{ij}=0}$$)行列を下三角行列という。上三角行列と下三角行列を合わせて三角行列という。
上三角行列$${U}$$と下三角行列$${L}$$の成分は以下のようになる。
$$
U=\begin{pmatrix}
a_{11}&a_{12}&\cdots&a_{1n}\\
&a_{22}&\cdots&a_{2n}\\
& &\ddots&\vdots\\
\huge{O}& & & a_{nn}
\end{pmatrix}
,
L=\begin{pmatrix}
a_{11}& & & \\
a_{21}&a_{22}& &\huge{O}\\
\vdots&\vdots&\ddots& \\
a_{n1}&a_{n2}&\cdots&a_{nn}
\end{pmatrix}
$$
上三角行列の例$${U_1}$$と下三角行列の例$${L_1}$$を以下に示す。
$$
U_1=\begin{pmatrix}
1&12&6& -2\\
0&-2& 2&3\\
0&0&3&-7\\
0&0&0&5
\end{pmatrix}
,
L_1=\begin{pmatrix}
8&0&0& 0\\
-4&5& 0&0\\
12&9&2&0\\
5&4&6&-3
\end{pmatrix}
$$
※行列の括弧について
行列の表記で
$$
A_4=\begin{bmatrix}
4 & 9 \\
1 & 7
\end{bmatrix}
$$
と書かれていることもある。
行列のベクトル表示
一般の行列$${A}$$は以下の列ベクトルを用いて$${A=(\bm{a}_1 \bm{a}_2 \cdots \bm{a}_n)}$$と表せる。
$$
\bm{a}_1=\begin{pmatrix}
a_{11}\\
a_{21}\\
\vdots\\
a_{m1}
\end{pmatrix}
,
\bm{a}_2=\begin{pmatrix}
a_{12}\\
a_{22}\\
\vdots\\
a_{m2}
\end{pmatrix}
,…,
\bm{a}_n=\begin{pmatrix}
a_{1n}\\
a_{2n}\\
\vdots\\
a_{mn}
\end{pmatrix}
$$
また、以下の行ベクトルを用いて
$$
A=\begin{pmatrix}
\bm{a}_1^{'}\\
\bm{a}_2^{'}\\
\vdots\\
\bm{a}_m^{'}
\end{pmatrix}
$$
とも表せる。
$${\bm{a}_1^{'}=(a_{11} a_{12} \cdots a_{1n}),\bm{a}_2^{'}=(a_{21} a_{22} \cdots a_{2n}),…,\bm{a}_m^{'}=(a_{m1} a_{m2} \cdots a_{mn})}$$
単位行列については、以下の$${n}$$次元基本列ベクトルを用いて$${I_n=(\bm{e}_1 \bm{e}_2 \cdots \bm{e}_n)}$$と表せる。
$$
\bm{e}_1=\begin{pmatrix}
1 \\
0 \\
\vdots\\
0
\end{pmatrix}
,
\bm{e}_2=\begin{pmatrix}
0 \\
1 \\
\vdots\\
0
\end{pmatrix}
,…,
\bm{e}_n=\begin{pmatrix}
0 \\
0 \\
\vdots\\
1
\end{pmatrix}
$$
また、以下の$${n}$$次元基本行ベクトルを用いて
$$
I_n=\begin{pmatrix}
\bm{e}_1^{'}\\
\bm{e}_2^{'}\\
\vdots\\
\bm{e}_n^{'}
\end{pmatrix}
$$
とも表せる。
$${\bm{e}_1^{'}=(1 0 \cdots 0),\bm{e}_2^{'}=(0 1 \cdots 0),…,\bm{e}_n^{'}=(0 0 \cdots 1)}$$
※前回も書いたが、行ベクトルはあまり使われない。
行列の転置
$${m \times n}$$の行列$${A}$$において、行と列を入れ替えた$${n \times m}$$の行列を$${A}$$の転置行列または行列$${A}$$の転置といい、$${A^T, {}^tA, A^{'}}$$などと表す。行列の$${(i,j)}$$成分が転置した行列の$${(j,i)}$$成分となる。($${A=(a_{ij})}$$のとき、$${A^T=(a_{ji})}$$となる)
行列$${A}$$とその転置$${A^T}$$の成分は以下のようになる。
$$
A=\begin{pmatrix}
a_{11}&a_{12}&\cdots&a_{1n}\\
a_{21}&a_{22}&\cdots&a_{2n}\\
\vdots&\vdots&&\vdots\\
a_{m1}&a_{m2}&\cdots&a_{mn}
\end{pmatrix}
,
A^T=\begin{pmatrix}
a_{11}&a_{21}&\cdots&a_{m1}\\
a_{12}&a_{22}&\cdots&a_{m2}\\
\vdots&\vdots&&\vdots\\
a_{1n}&a_{2n}&\cdots&a_{mn}
\end{pmatrix}
$$
※第1行の成分を第1列に並べる、第1列の成分を第1行に並べるといった操作をすればよい。
※正方行列の転置は、対角成分に関して成分を対称移動させるイメージである。
行列の転置の例を以下に示す。
$$
A_3=\begin{pmatrix}
1 & -2 & 3 \\
10 & 6 & 0
\end{pmatrix}
,
A_3^T=\begin{pmatrix}
1 & 10 \\
-2 & 6 \\
3 & 0
\end{pmatrix}
\\
A_4=\begin{pmatrix}
4 & 9 \\
1 & 7
\end{pmatrix}
,
A_4^{T}=\begin{pmatrix}
4 & 1 \\
9 & 7
\end{pmatrix}
$$
列ベクトルを転置すると、行ベクトルになる。列ベクトル$${\bm{a}}$$とその転置$${\bm{a}^T}$$の成分は以下のようになる。
$$
\bm{a}=\begin{pmatrix}
a_{1}\\
a_{2}\\
\vdots\\
a_{m}
\end{pmatrix}
,
\bm{a}^T=\begin{pmatrix}
a_{1}&a_{2}&\cdots&a_{m}
\end{pmatrix}
$$
転置行列を転置すると、もとの行列になる。つまり、$${(A^T)^T=A}$$である。
行列の相等と演算
行列の相等
$${m\times n}$$の行列$${A,B}$$に対して、すべての成分が等しいとき、行列$${A}$$と$${B}$$は等しいといい、$${A=B}$$と表す。この定義は以下のように書くことができる。
$${a_{ij}=b_{ij} \space (i = 1,2, …,m ; j =1,2,…,n)}$$
※サイズが等しい行列どうしでなければならない。
行列の和・差
$${m\times n}$$の行列$${A,B}$$に対して、その和と差は以下のようになる。
$$
A+B=(a_{ij}+b_{ij})=\begin{pmatrix}
a_{11}+b_{11}&a_{12}+b_{12}&\cdots&a_{1n}+b_{1n}\\
a_{21}+b_{21}&a_{22}+b_{22}&\cdots&a_{2n}+b_{2n}\\
\vdots&\vdots&&\vdots\\
a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots&a_{mn}+b_{mn}
\end{pmatrix}
\\
A-B=(a_{ij}-b_{ij})=\begin{pmatrix}
a_{11}-b_{11}&a_{12}-b_{12}&\cdots&a_{1n}-b_{1n}\\
a_{21}-b_{21}&a_{22}-b_{22}&\cdots&a_{2n}-b_{2n}\\
\vdots&\vdots&&\vdots\\
a_{m1}-b_{m1}&a_{m2}-b_{m2}&\cdots&a_{mn}-b_{mn}\\
\end{pmatrix}
$$
※サイズが等しい行列どうしでなければならない。
行列のスカラー倍
行列$${A}$$に対して、そのスカラー倍は以下のようになる。
$$
kA=(ka_{ij})=\begin{pmatrix}
ka_{11}&ka_{12}&\cdots&ka_{1n}\\
ka_{21}&ka_{22}&\cdots&ka_{2n}\\
\vdots&\vdots&&\vdots\\
ka_{m1}&ka_{m2}&\cdots&ka_{mn}
\end{pmatrix}
(k \in \mathbb{R})
$$
行列の積
$${m\times n}$$の行列$${A}$$と$${n\times l}$$の行列$${B}$$に対して、その積は以下のようになる。
$$
\begin{aligned}
AB&=\begin{pmatrix}
a_{11}&a_{12}&\cdots&a_{1n}\\
a_{21}&a_{22}&\cdots&a_{2n}\\
\vdots&\vdots&&\vdots\\
a_{i1}&a_{i2}&\cdots&a_{in}\\
\vdots&\vdots&&\vdots\\
a_{m1}&a_{m2}&\cdots&a_{mn}
\end{pmatrix}
\begin{pmatrix}
b_{11}&b_{12}&\cdots&b_{1j}&\cdots&b_{1l}\\
b_{21}&b_{22}&\cdots&b_{2j}&\cdots&b_{2l}\\
\vdots&\vdots&&\vdots&&\vdots\\
b_{n1}&b_{n2}&\cdots&b_{nj}&\cdots&b_{nl}
\end{pmatrix}\\
&=\begin{pmatrix}
c_{11}&c_{12}&\cdots&c_{1j}&\cdots&c_{1l}\\
c_{21}&c_{22}&\cdots&c_{2j}&\cdots&c_{2l}\\
\vdots&\vdots&&\vdots&&\vdots\\
c_{i1}&c_{i2}&\cdots&c_{ij}&\cdots&c_{il}\\
\vdots&\vdots&&\vdots&&\vdots\\
c_{m1}&c_{m2}&\cdots&c_{mj}&\cdots&c_{ml}
\end{pmatrix}
\end{aligned}
\\
c_{ij}=\displaystyle\sum_{k=1}^n{a_{ik}b_{kj}}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots+a_{in}b_{nj}
$$
※行列の積は、左の行列の列数と右の行列の行数が一致している行列どうしでなければ計算できない。
$${n}$$個の正方行列$${A}$$の積を$${A}$$の$${n}$$乗といい、$${A^n}$$と表す。
行列$${A,B}$$の積$${AB}$$の求め方
行列$${A}$$のサイズが$${m\times n}$$、行列$${B}$$のサイズが$${n \times l}$$のとき、積$${AB}$$のサイズは$${m \times l}$$となる
サイズに注目すると、
$${(m\times \underline{n})\times(\underline{n}\times l)=(m\times l)}$$となる。このとき、下線の部分が一致していることが積が計算できるかどうかにおいて重要である
各成分については、例えば$${AB}$$の$${(1,2)}$$成分を求めるには、$${A}$$の第1行の要素と$${B}$$の第2列の要素を順に1つずつかけたものを足せばよい
行列の積の例を以下に示す。
$$
A=\begin{pmatrix}
1&2&5\\
-1&3&2
\end{pmatrix}
,
B=\begin{pmatrix}
6&1&4\\
2&1&0\\
3&4&-3
\end{pmatrix}
\\
\begin{aligned}
AB&=\begin{pmatrix}
1\cdot6+2\cdot2+5\cdot3&1\cdot1+2\cdot1+5\cdot4&1\cdot4+2\cdot0+5\cdot(-3)\\
(-1)\cdot6+3\cdot2+2\cdot3&(-1)\cdot1+3\cdot1+2\cdot4&(-1)\cdot4+3\cdot0+2\cdot(-3)
\end{pmatrix}
\\
&=\begin{pmatrix}
25&12&-11\\
6&10&-10
\end{pmatrix}
\end{aligned}
$$
※行列$${A}$$のサイズは、$${2\times3}$$、$${B}$$のサイズは$${3\times3}$$で、$${AB}$$のサイズは$${(2\times3)\times(3\times3)=2\times3}$$となっている。
行列の演算の性質
ここでは、これまでに定義した行列の演算についての法則をまとめて紹介する。証明については、一部を演習問題とし、他は省略する。
以下、$${k,l \in \mathbb{R},A,B,C}$$は行列ですべて演算が定義できるものとする。
・同じ行列どうしの演算
$${A+A=2A,A-A=O,-A+A=O}$$
・零行列との演算
$${A+O=A,A-O=A,kO=O,AO=O,OA=O}$$
・単位行列との演算
$${AI=A,IA=A}$$
・交換法則(演算の順序を交換できる)
$${A+B=B+A}$$
※行列の積では、交換法則が成り立たない。
・結合法則(演算の優先順位を変更しても結果は変わらない)
$${(A+B)+C=A+(B+C),k(lA)=(kl)A,(AB)C=A(BC)}$$
・分配法則(演算は掛け算のように展開することができる)
$${k(A+B)=kA+kB,(k+l)A=kA+lA,(A+B)C=AC+BC,A(B+C)=AB+AC}$$
・スカラー倍
$${1A=A,0A=O,(kA)B=A(kB)=k(AB)}$$
・転置
$${O^T=O,I^T=I,(A+B)^T=A^T+B^T,(kA)^T=kA^T,(AB)^T=B^TA^T}$$
・トレース
$${\text{tr}(A+B)=\text{tr}(A)+\text{tr}(B),\text{tr}(kA)=k\text{tr}(A),\text{tr}(A^T)=\text{tr}(A),\text{tr}(AB)=\text{tr}(BA)}$$
※トレースは正方行列において定義されていることに注意する。
以下で、上の性質について補足説明をする。
単位行列は実数の積における1と同じ働きをする。(単位行列は乗法単位元である)零行列は実数の和における0と同じ働きをする。(零行列は加法単位元である)
$${A \neq O, B \neq O}$$について、$${AB=O}$$となるとき、行列$${A,B}$$を零因子という。
一般に行列の積において、交換法則は成り立たず、非可換である。(可換とは$${AB=BA}$$が成り立つことをいう)ただし、$${AB=BA}$$が成り立つこともある。
このことから、行列の等式変形において両辺に行列をかけるとき、左からかけるか、右からかけるかということが明記されることが多い。
行列の分割と積
行列を縦線と横線で区切って、小さなブロックに分けると、行列の積の計算が楽になることがある。このとき、分けられた各ブロックをブロック行列または小行列という。
一般に$${M\times N}$$の行列$${A}$$と$${N\times L}$$の行列$${B}$$に対して、行列をブロックごとに分割したとき、積$${AB}$$は以下のようになる。
$$
A=\begin{pmatrix}
A_{11}&A_{12}&\cdots&A_{1q}\\
A_{21}&A_{22}&\cdots&A_{2q}\\
\vdots&\vdots&&\vdots\\
A_{p1}&A_{p2}&\cdots&A_{pq}
\end{pmatrix}
,B=\begin{pmatrix}
B_{11}&B_{12}&\cdots&B_{1r}\\
B_{21}&B_{22}&\cdots&B_{2r}\\
\vdots&\vdots&&\vdots\\
B_{q1}&B_{q2}&\cdots&B_{qr}
\end{pmatrix}
\\A_{1k},A_{2k},..,A_{pk}\text{の列数}=B_{k1},B_{k2},..,B_{kr}\text{の行数}=N_k;
\displaystyle\sum_{k=1}^qN_k=N\\
AB=\begin{pmatrix}
C_{11}&C_{12}&\cdots&C_{1j}&\cdots&C_{1r}\\
C_{21}&C_{22}&\cdots&C_{2j}&\cdots&C_{2r}\\
\vdots&\vdots&&\vdots&&\vdots\\
C_{i1}&C_{i2}&\cdots&C_{ij}&\cdots&C_{ir}\\
\vdots&\vdots&&\vdots&&\vdots\\
C_{p1}&C_{p2}&\cdots&C_{pj}&\cdots&C_{pr}
\end{pmatrix}
\\
C_{ij}=\displaystyle\sum_{k=1}^q{A_{ik}B_{kj}}=A_{i1}B_{1j}+A_{i2}B_{2j}+\cdots+A_{iq}B_{qj}
$$
このように、行列を分割した場合の積の計算は各ブロック行列を、行列の各成分とみたときの行列の積の計算式と一致する。ただし、積を計算する$${A}$$の各ブロック行列の列数と$${B}$$の各ブロック行列の行数が同じである必要がある。
特に、ブロック行列の中に零行列や単位行列があるときに計算が楽になる。
行列の分割による積の計算例を以下に示す。
$$
\begin{aligned}
&\begin{pmatrix}
1&0&3\\
0&1&7\\
0&0&6
\end{pmatrix}
\begin{pmatrix}
-2&0&2&0\\
0&-1&3&0\\
2&4&1&4
\end{pmatrix}\\
&=\begin{pmatrix}
\begin{array}{cc|c}
1&0&3\\
0&1&7\\ \hline
0&0&6
\end{array}
\end{pmatrix}
\begin{pmatrix}
\begin{array}{ccc|c}
-2&0&2&0\\
0&-1&3&0\\ \hline
2&4&1&4
\end{array}
\end{pmatrix}\\
&=\begin{pmatrix}
I_2&A_{12}\\
O&A_{22}
\end{pmatrix}
\begin{pmatrix}
B_{11}&O\\
B_{21}&B_{22}
\end{pmatrix}\\
&=\begin{pmatrix}
I_2B_{11}+A_{12}B_{21}&I_2O+A_{12}B_{22}\\
OB_{11}+A_{22}B_{21}&OO+A_{22}B_{22}
\end{pmatrix}\\
&=\begin{pmatrix}
B_{11}+A_{12}B_{21}&A_{12}B_{22}\\
A_{22}B_{21}&A_{22}B_{22}
\end{pmatrix}
\end{aligned}
\\
B_{11}+A_{12}B_{21}=\begin{pmatrix}
-2&0&2\\
0&-1&3
\end{pmatrix}
+\begin{pmatrix}
6&12&3\\
14&28&7
\end{pmatrix}
=\begin{pmatrix}
4&12&5\\
14&27&10
\end{pmatrix}
\\
A_{12}B_{22}=\begin{pmatrix}
12\\
28
\end{pmatrix}\\
A_{22}B_{21}=\begin{pmatrix}
12&24&6
\end{pmatrix}\\
A_{22}B_{22}=24\\
\begin{pmatrix}
B_{11}+A_{12}B_{21}&A_{12}B_{22}\\
A_{22}B_{21}&A_{22}B_{22}
\end{pmatrix}
=\begin{pmatrix}
4&12&5&12\\
14&27&10&28\\
12&24&6&24
\end{pmatrix}\\
$$
※分割するとき、ブロック行列のサイズが積の計算が可能なものになるように注意する。
上で説明した行列のベクトル表示も分割の一つである。これを用いることで例えば、以下のような計算を行列とベクトルの積で表現することができる。
$${A=(\bm{a}_1 \bm{a}_2 \cdots \bm{a}_n),\bm{x}=(x_1 x_2 \cdots x_n)^T,\bm{y}=(y_1 y_2 \cdots y_n)^T}$$のとき、$${y_i=\displaystyle\sum_{k=1}^na_{ik}x_k (i=1,2,…,n)}$$を$${\bm{y}=A\bm{x}=\displaystyle\sum_{k=1}^nx_k\bm{a}_k}$$とすべての$${i}$$について1つの式で表せる。
※行列とベクトルの積で表すことで、例えばプログラミングでの実装が楽になる。
様々な行列
ここでは、行列の等式によって定義される様々な行列を紹介する。なお、求め方についてなど、詳しくは後でこのシリーズで取り扱う。
正則行列・逆行列
$${n}$$次正方行列$${A}$$において、$${XA=AX=I_n}$$を満たす$${n}$$次正方行列$${X}$$が存在するとき、$${A}$$は正則であるといい、$${A}$$を正則行列という。また、このとき$${X}$$を$${A}$$の逆行列といい、$${A^{-1}}$$($${A}$$インバース)と表す。
※上の説明において、$${X}$$を正則行列、$${A}$$を$${X}$$の逆行列といいかえることもできる。
逆行列は実数の商における割る数と同じ働きをする。ただし、$${\dfrac{1}{A}}$$とは書かず、逆行列をかけることで演算を行う。
正方行列において、逆行列が存在しないこともある。また、逆行列は一意に表せる。(ある正方行列に対して、逆行列が存在するならばただ一つである)
2次正方行列の逆行列は以下の公式を用いて求めることができる。
$$
A=\begin{pmatrix}
a&b\\
c&d
\end{pmatrix}
に対して, ad-bc\neq 0 のときA^{-1}が存在し,\\
A^{-1}=\dfrac{1}{ad-bc}\begin{pmatrix}
d&-b\\
-c&a
\end{pmatrix}
\\また, ad-bc=0のときA^{-1}は存在しない.
$$
※$${ad-bc}$$は$${A}$$の行列式である。ただし、行列式については、後でこのシリーズで説明する。
以下に逆行列の性質をまとめて紹介する。証明については、一部を演習問題とし、他は省略する。
$${A,B}$$は$${n}$$次正方行列、$${k\in \mathbb{R},k\neq 0}$$とする。
$${I^{-1}=I}$$
$${(A^{-1})^{-1}=A}$$
$${A,B}$$が正則であるとき、$${AB}$$は正則行列で、$${(AB)^{-1}=B^{-1}A^{-1}}$$
$${(kA)^{-1}=\dfrac{1}{k}A^{-1}}$$
$${A}$$が正則であるとき、$${A^T}$$は正則行列で、$${(A^T)^{-1}=(A^{-1})^T}$$
直交行列
$${n}$$次正方行列$${A}$$において、$${AA^T=A^TA=I_n}$$が成り立つとき、$${A}$$を直交行列という。
※「直行行列」ではないので、注意する。
以下に直交行列の性質をまとめて紹介する。証明については、すべて演習問題としている。
$${A,B}$$は$${n}$$次正方行列とする。
$${A,B}$$が直交行列のとき、$${AB}$$は直交行列である
$${A}$$が直交行列のとき、$${A^{-1},A^T}$$は直交行列で、$${A^{-1}=A^T}$$である
対称行列・交代行列
$${n}$$次正方行列$${A}$$において、$${A^T=A}$$が成り立つとき、$${A}$$を対称行列という。また、$${A^T=-A}$$が成り立つとき、$${A}$$を交代行列または反対称行列という。
以下に対称行列・交代行列の性質をまとめて紹介する。証明については、一部を演習問題とし、他は省略する。
$${A,B}$$は$${n}$$次正方行列、$${k\in \mathbb{R}}$$とする。
$${A,B}$$が対称行列のとき、$${A+B,kA,A+A^T,AA^T}$$は対称行列である
$${A,B}$$が交代行列のとき、$${A+B,kA,A-A^T,-AA^T}$$は交代行列である
演習問題2
問題3 以下の行列$${A,B,C}$$に対して、次の各問に答えよ。
$$
A=\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix},
B=\begin{pmatrix}
2&4\\
1&2
\end{pmatrix},
C=\begin{pmatrix}
0&3&4\\
8&7&3
\end{pmatrix}
$$
(1)$${A+B,A-2B,AB,BA,AC,CA,ABC}$$をそれぞれ求めよ。ただし、計算が定義できないものは「定義できない」と答えよ。
(2)$${A^2,B^2,(A-B)^2,(A+2B)(B-I_2)}$$をそれぞれ求めよ。
(3)$${A^{-1},B^{-1},A^T,(A^{-1})^T,(A^T)^{-1}}$$をそれぞれ求めよ。ただし、逆行列が存在しないものは「正則ではない」と答えよ。
(4)$${CX=O_{22}}$$を満たす行列$${X}$$を求めよ。
(5)$${Y-Z=A,2Y+3Z=B}$$を満たす行列$${Y,Z}$$を求めよ。
[方針]
(2)の$${(A-B)^2}$$などの計算では、$${A-B}$$を求めてないが、ここまでで$${A^2,B^2,AB,BA}$$を求めているので、展開すれば簡単に求められる。ただし、行列の積は非可換であるので数と同様に展開公式を適用できないことに注意する。
(4)の$${X}$$のサイズは、積の計算が$${(2\times 3)\times X=(2\times2)}$$より$${3\times2}$$とわかる。
[解答]
(1)
$$
A+B=\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}
+\begin{pmatrix}
2&4\\
1&2
\end{pmatrix}
=\begin{pmatrix}
4&4\\
0&6
\end{pmatrix}
\\
A-2B=\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}
-2\begin{pmatrix}
2&4\\
1&2
\end{pmatrix}
=\begin{pmatrix}
-2&-8\\
-3&0
\end{pmatrix}
\\
\begin{aligned}
AB&=\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}
\begin{pmatrix}
2&4\\
1&2
\end{pmatrix}
\\
&=\begin{pmatrix}
2\cdot2+0\cdot1&2\cdot4+0\cdot2\\
(-1)\cdot2+4\cdot1&(-1)\cdot4+4\cdot2
\end{pmatrix}
\\
&=\begin{pmatrix}
4&8\\
2&4
\end{pmatrix}
\\
BA&=\begin{pmatrix}
2&4\\
1&2
\end{pmatrix}
\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}
\\
&=\begin{pmatrix}
2\cdot2+4\cdot(-1)&2\cdot0+4\cdot4\\
1\cdot2+2\cdot(-1)&1\cdot0+2\cdot4
\end{pmatrix}
\\
&=\begin{pmatrix}
0&16\\
0&8
\end{pmatrix}
\\
AC&=\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}
\begin{pmatrix}
0&3&4\\
8&7&3
\end{pmatrix}
\\
&=\begin{pmatrix}
2\cdot0+0\cdot8&2\cdot3+0\cdot7&2\cdot4+0\cdot3\\
(-1)\cdot0+4\cdot8&(-1)\cdot3+4\cdot7&(-1)\cdot4+4\cdot3
\end{pmatrix}
\\
&=\begin{pmatrix}
0&6&8\\
32&25&8
\end{pmatrix}
\\
\end{aligned}
\\
CAは, 行列Cのサイズ2\times3, Aのサイズ2\times2より定義できない
\\
\begin{aligned}
ABC&=(AB)C
\\&=\begin{pmatrix}
4&8\\
2&4
\end{pmatrix}
\begin{pmatrix}
0&3&4\\
8&7&3
\end{pmatrix}
\\
&=\begin{pmatrix}
4\cdot0+8\cdot8&4\cdot3+8\cdot7&4\cdot4+8\cdot3\\
2\cdot0+4\cdot8&2\cdot3+4\cdot7&2\cdot4+4\cdot3
\end{pmatrix}
\\
&=\begin{pmatrix}
64&68&40\\
32&34&20
\end{pmatrix}
\\
\end{aligned}
$$
(2)
$$
\begin{aligned}
A^2&=\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}
\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}
\\
&=\begin{pmatrix}
2\cdot2+0\cdot(-1)&2\cdot0+0\cdot4\\
-1\cdot2+4\cdot(-1)&-1\cdot0+4\cdot4
\end{pmatrix}
\\
&=\begin{pmatrix}
4&0\\
-6&16
\end{pmatrix}
\\
B^2&=\begin{pmatrix}
2&4\\
1&2
\end{pmatrix}
\begin{pmatrix}
2&4\\
1&2
\end{pmatrix}
\\
&=\begin{pmatrix}
2\cdot2+4\cdot1&2\cdot4+4\cdot2\\
1\cdot2+2\cdot1&1\cdot4+2\cdot2
\end{pmatrix}
\\
&=\begin{pmatrix}
8&16\\
4&8
\end{pmatrix}
\\
(A-B)^2&=(A-B)(A-B)
\\&=A^2-AB-BA+B^2
\\&=\begin{pmatrix}
4&0\\
-6&16
\end{pmatrix}
-\begin{pmatrix}
4&8\\
2&4
\end{pmatrix}
-\begin{pmatrix}
0&16\\
0&8
\end{pmatrix}
+\begin{pmatrix}
8&16\\
4&8
\end{pmatrix}
\\&=\begin{pmatrix}
8&-8\\
-4&12
\end{pmatrix}
\\
(A+2B)(B-I_2)&=AB-AI_2+2B^2-2BI_2
\\&=AB-A+2B^2-2B
\\&=\begin{pmatrix}
4&8\\
2&4
\end{pmatrix}
-\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}
+2\begin{pmatrix}
8&16\\
4&8
\end{pmatrix}
-2\begin{pmatrix}
2&4\\
1&2
\end{pmatrix}
\\&=\begin{pmatrix}
14&32\\
9&12
\end{pmatrix}
\end{aligned}
$$
(3)
$$
A^{-1}=\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}^{-1}
=\dfrac{1}{2\cdot4-0\cdot(-1)}\begin{pmatrix}
4&0\\
1&2
\end{pmatrix}
=\begin{pmatrix}
\dfrac{1}{2}&0\\
\\
\dfrac{1}{8}&\dfrac{1}{4}
\end{pmatrix}
\\Bは, 2\cdot2-4\cdot1=0より正則ではない
\\A^T=\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}^T
=\begin{pmatrix}
2&-1\\
0&4
\end{pmatrix}
\\(A^{-1})^T=\begin{pmatrix}
\dfrac{1}{2}&0\\
\\
\dfrac{1}{8}&\dfrac{1}{4}
\end{pmatrix}^T
=\begin{pmatrix}
\dfrac{1}{2}&\dfrac{1}{8}\\
\\
0&\dfrac{1}{4}
\end{pmatrix}
\\(A^T)^{-1}=\begin{pmatrix}
2&-1\\
0&4
\end{pmatrix}^{-1}
=\dfrac{1}{2\cdot4-(-1)\cdot0}\begin{pmatrix}
4&1\\
0&2
\end{pmatrix}
=\begin{pmatrix}
\dfrac{1}{2}&\dfrac{1}{8}\\
\\
0&\dfrac{1}{4}
\end{pmatrix}
$$
(4)
$$
X=\begin{pmatrix}
a&b\\
c&d\\
e&f
\end{pmatrix}
とおく.
\\
\begin{aligned}
CX&=O_{22}
\\
\begin{pmatrix}
0&3&4\\
8&7&3
\end{pmatrix}
\begin{pmatrix}
a&b\\
c&d\\
e&f
\end{pmatrix}
&=\begin{pmatrix}
0&0\\
0&0
\end{pmatrix}
\\
\begin{pmatrix}
3c+4e&3d+4f\\
8a+7c+3e&8b+7d+3f
\end{pmatrix}
&=\begin{pmatrix}
0&0\\
0&0
\end{pmatrix}
\end{aligned}
\\
\begin{cases}
\begin{aligned}
3c+4e&=0\therefore e=-\dfrac{3}{4}c\\
3d+4f&=0\therefore f=-\dfrac{3}{4}d\\
8a+7c+3e&=0\therefore c=-\dfrac{32}{19}a\\
8b+7d+3f&=0\therefore d=-\dfrac{32}{19}b\\
\end{aligned}
\end{cases}
\\
\therefore c=-\dfrac{32}{19}a, d=-\dfrac{32}{19}b, e=-\dfrac{3}{4}c=\dfrac{24}{19}a, f=-\dfrac{3}{4}d=\dfrac{24}{19}b
\\
X=\begin{pmatrix}
a&b\\
-\frac{32}{19}a&-\frac{32}{19}b\\
\frac{24}{19}a&\frac{24}{19}b
\end{pmatrix}
=\dfrac{1}{19}a\begin{pmatrix}
19&0\\
-32&0\\
24&0
\end{pmatrix}
+\dfrac{1}{19}b\begin{pmatrix}
0&19\\
0&-32\\
0&24
\end{pmatrix}
(a,b\in \Bbb{R})
$$
(5)
$$
\begin{cases}
\begin{aligned}
Y−Z&=A&\cdots \text{\textcircled 1}\\
2Y+3Z&=B&\cdots \text{\textcircled 2}
\end{aligned}
\end{cases}
\\
\text{\textcircled 1}\times 3+\text{\textcircled 2}より\\
5Y=3A+B=3\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}
+\begin{pmatrix}
2&4\\
1&2
\end{pmatrix}
=\begin{pmatrix}
8&4\\
-2&14
\end{pmatrix}
\\
\therefore Y=\dfrac{1}{5}\begin{pmatrix}
8&4\\
-2&14
\end{pmatrix}
\\
\text{\textcircled 1}\times 2-\text{\textcircled 2}より\\
-5Z=2A-B=2\begin{pmatrix}
2&0\\
-1&4
\end{pmatrix}
-\begin{pmatrix}
2&4\\
1&2
\end{pmatrix}
=\begin{pmatrix}
2&-4\\
-3&6
\end{pmatrix}
\\
\therefore Z=\dfrac{1}{5}\begin{pmatrix}
-2&4\\
3&-6
\end{pmatrix}
$$
※(2)について、$${(A-B)^2}$$を求めるために、$${A-B}$$を計算し、それを2乗してもよい。
(4)について、$${\dfrac{1}{19}a\rightarrow a, \dfrac{1}{19}b\rightarrow b}$$とおきかえて、
$$
X=a\begin{pmatrix}
19&0\\
-32&0\\
24&0
\end{pmatrix}
+b\begin{pmatrix}
0&19\\
0&-32\\
0&24
\end{pmatrix}
(a,b\in \Bbb{R})
$$
としてもよい。
問題4 次のことを証明せよ。
(1)$${m \times n}$$の行列$${A}$$と$${n \times l}$$の行列$${B}$$に対して、$${(AB)^T=B^TA^T}$$が成り立つ
(2)$${n}$$次正方行列$${A}$$,$${B}$$に対して、$${\text{tr}(AB)=\text{tr}(BA)}$$が成り立つ
(3) 正則行列$${A}$$に対して、その逆行列は一意に表せる
(4) $${A,B}$$が正則行列のとき、$${AB}$$は正則行列で、$${(AB)^{-1}=B^{-1}A^{-1}}$$である
(5)$${A}$$が正則行列のとき、$${A^T}$$は正則行列で、$${(A^T)^{-1}=(A^{-1})^T}$$である
(6)$${A,B}$$が直交行列のとき、$${AB}$$は直交行列である
(7)$${A}$$が直交行列のとき、$${A^{-1},A^T}$$は直交行列で、$${A^{-1}=A^T}$$である
(8)$${A,B}$$が対称行列のとき、$${A+B}$$は対称行列である
(9)$${A}$$が対称行列のとき、$${AA^T}$$は対称行列である
(10)$${A}$$が交代行列のとき、$${A-A^T}$$は交代行列である
[方針]
用語の定義と性質を利用すると証明できる。
[証明]
(1)
$$
\begin{aligned}
(AB)^Tの(i,j)成分&=ABの(j,i)成分\\
&=\displaystyle\sum_{k=1}^na_{jk}b_{ki}\\
&=\displaystyle\sum_{k=1}^nb_{ki}a_{jk}\\
&=\displaystyle\sum_{k=1}^n(B^Tの(i,k)成分)(A^Tの(k,j)成分)\\
&=B^TA^Tの(i,j)成分
\end{aligned}
\\\hspace{30em}\Box
$$
(2)
$$
ABの対角成分((i,i)成分)a_{i1}b_{1i}+a_{i2}b_{2i}+…+a_{in}b_{ni}より\\
\begin{aligned}
\text{tr}(AB)&=\displaystyle\sum_{i=1}^n(a_{i1}b_{1i}+a_{i2}b_{2i}+…+a_{in}b_{ni})\\
&=\displaystyle\sum_{i=1}^n(b_{1i}a_{i1}+b_{2i}a_{i2}+…+b_{ni}a_{in})
\end{aligned}
\\
BAの対角成分((i,i)成分)b_{1i}a_{i1}+b_{2i}a_{i2}+…+b_{ni}a_{in}より\\
\hspace{5em}\text{tr}(AB)=\text{tr}(BA)
\hspace{15em}\Box
$$
(3)
$$
Aの逆行列が2つ存在すると仮定する\\
つまり, AB=BA=I, AC=CA=Iを満たす行列B,Cが存在する\\
\begin{aligned}
B&=BI\\
&=B(AC) (\because AC=I)\\
&=(BA)C\\
&=IC (\because BA=I)\\
&=C
\end{aligned}
\\
よって, Aの逆行列は一意に表せる
\hspace{15em}\Box
$$
(4)
$$
A,Bは正則行列よりA^{-1},B^{-1}が存在する\\
(AB)(B^{-1}A^{-1})=A(BB^{-1})A^{-1}=AIA^{-1}=AA^{-1}=I\\
(B^{-1}A^{-1})(AB)=B^{-1}(A^{-1}A)B=B^{-1}IB=B^{-1}B=I\\
よって, (AB)(B^{-1}A^{-1})=(B^{-1}A^{-1})(AB)=I\\
ABは正則行列で, (AB)^{-1}=B^{-1}A^{-1}
\hspace{10em}\Box
$$
(5)
$$
Aは正則行列よりA^{-1}が存在する\\
A^T(A^{-1})^T=(A^{-1}A)^T=I^T=I (\because (1))\\
(A^{-1})^TA^T=(AA^{-1})^T=I^T=I (\because (1))\\
よって, A^T(A^{-1})^T=(A^{-1})^TA^T=I\\
A^Tは正則行列で, (A^T)^{-1}=(A^{-1})^T
\hspace{5em}\Box
$$
(6)
$$
A,Bは直交行列よりAA^T=A^TA=I, BB^T=B^TB=I\\
(AB)(AB)^T=(AB)(B^TA^T)=A(BB^T)A^T=AIA^T=AA^T=I\\
(AB)^T(AB)=(B^TA^T)(AB)=B^T(A^TA)B=B^TIB=B^TB=I\\
よって, (AB)(AB)^T=(AB)^T(AB)=I\\
ABは直交行列である
\hspace{20em}\Box
$$
(7)
$$
Aは直交行列よりAA^T=A^TA=I\\
A^{-1}(A^{-1})^T=A^{-1}(A^T)^{-1}=(A^TA)^{-1}=I^{-1}=I (\because(4))\\
(A^{-1})^TA^{-1}=(A^T)^{-1}A^{-1}=(AA^T)^{-1}=I^{-1}=I (\because(4))\\
よって, A^{-1}(A^{-1})^T=(A^{-1})^TA^{-1}=I\\
A^{-1}は直交行列である\\
また, AA^T=A^TA=Iより, A^{-1}=A^T\\
よって, A^Tも直交行列である
\hspace{15em}\Box
$$
(8)
$$
A,Bは対称行列よりA^T=A, B^T=B\\
(A+B)^T=A^T+B^T=A+B\\
よって, A+Bは対称行列である
\hspace{5em}\Box
$$
(9)
$$
Aは対称行列よりA^T=A\\
(AA^T)^T=(A^T)^TA^T=A^TA^T=AA^T\\
よって, AA^Tは対称行列である
\hspace{5em}\Box
$$
(10)
$$
Aは交代行列よりA^T=-A\\
(A-A^T)^T=A^T-(A^T)^T=-A-(-A^T)=-(A-A^T)\\
よって, A-A^Tは交代行列である
\hspace{10em}\Box
$$
※このような性質(定理)の証明に慣れておくと、抽象的な数学の議論を理解しやすくなる。
問題5 $${A}$$が正則行列のとき、$${AX=B}$$を満たす行列$${X}$$を求めよ。
[方針]
行列の積は非可換であるので、等式変形において両辺に行列をかけるとき、左からかけるか、右からかけるかによって結果が変わることに注意する。
[解答]
$$
Aは正則行列より, A^{-1}が存在する\\
\begin{aligned}
AX&=B\\
両辺に左からA^{-1}をかけると\\
A^{-1}AX&=A^{-1}B\\
IX&=A^{-1}B\\
X&=A^{-1}B
\end{aligned}
$$
最後に
今回は、大学数学・線形代数の解説記事として、行列の基礎とその演算に加えて、これから登場する様々な行列の定義と簡単な性質を解説しました。今回も、解説と演習問題とでかなりの量だったので、書くのが大変でした。次回は、2次正方行列のn乗の解説記事となる予定です。では。
この記事の続きは以下の記事です。
