
勉強に関する記事
・効果的な勉強方法
・モンティーホール問題
モンティ・ホール問題とは、数学史上最も議論を巻き起こした確率の問題。
この問題を最短で解説します。
問題は次の通りです。
A、B、Cの3つのドアがあります。
そのうち1つのドアは「あたり」で、残りの2つのドアは「ハズレ」です。
あなたは、3つのうちどれか1つのドアを選びます。
残り2つのうち1つのドアが開けられて「ハズレ」が示されます。
このとき選んだドアをそのままにしておくのと、残りの開いていないドアに変更するのでは、どちらが「あたり」を出す可能性が高いのか?
まず、この問題文の解釈を少し変えてみます。
「残りの2つのうち1つのドアが開く」ということは、自分が選んだ後に開くのは必ずハズレのドアという意味です。
つまり、「自分がドアを選んだ後、ハズレの扉が開く」と解釈を変えておきます。
すると、次のように考えることができます。

(1) Aがあたりで、Aのドアを選んだとき
BかCのドアが開きます。
この場合、最初に選んだドアを変えるとハズレを選ぶことになるので、変えない方がいいことになります。
(2) Aがあたりで、Bのドアを選んだとき
Cのドアが開きます。
この場合、変えるとあたりのドアに行くことができます。
(3) Aがあたりで、Cのドアを選んだとき
Bのドアが開きます。
この場合も、変えるとあたりのドアに行くことができます。
つまり、Aがあたりのときは、最初に選んだドアを変えることで当たる確率が2倍になることが分かります。
Bがあたりのときも、Cがあたりのときも同様なので、ハズレのドアが開いた後にドアを変えた方がいいことになります。
よって、「変更した方があたりを引く確率が上がる」が正解になります。
・英語に関する記事
英単語01『arm』
さて、初回は『Arm』について書いてみたいと思います。
この言葉は『腕』という意味で知られていますが、もともとは、『肩と上手くつなぎ合わせたもの』という意味です。
何かと何かをつなぎ合わせて作りだされたものといえば『武器』がありますが、沢山の部品をつなぎ合わせていることから『Arms』と複数にして扱われています。
・armadillo(アルマジロ)
arm(武器)→武装したもの→アルマジロ
アルマジロという動物をご存じでしょうか?

この動物、背中をよく見たら『武装』しているように見えますよね…。
なので、この動物を発見した人が『武装したもの』ということで、『Armadillo』と名づけたそうです。
・army(軍隊)
arm(武器)+y(集団)→武器を所持するもの→軍隊
・alarm(目覚まし時計)
al(~の方へ)+arm(武器)→警報→恐怖→目が覚める→目覚まし時計
どうして、武器の方向に行くことが目覚ましになるのかというと、戦争の時代の集合や警報のサインだったわけですね。
・armor(鎧兜)
arm(武器)+or(もの)→武器をセットにあるもの→鎧兜
鎧とか兜って、武器と関係が深いですよね。
・disarmament(武装解除)
dis(~でない)+arm(武器)+ment(こと)→武器を捨てること→武装解除
英単語02『bar』
みなさんは『Bar』といえば、何を想像するでしょうか?
『棒』のこと?
それとも、『酒場』のこと?
このどちらかを想像する人が多いと思います。
そもそも、『Bar』という言葉はどうして『棒』と『酒場』という意味があるのでしょうか?
実は、『Bar』というのは本当は『横木』という意味なのです。
・bar(酒場)
古代の酒場は横木を置いて、それを境にしてお酒を提供する人とお酒を飲む人を分けていたのです。
察しがいい人は分かったと思いますが、それが今でいう『カウンター』です。
なので、酒場というのは横木を利用していたことから、『Bar』と呼ぶようになったのです。
・bar(裁判所)
どうして裁判所という意味があるのかというと、法廷と傍聴席の間には『横木』を置いて仕切っていたのです。
今でも、裁判所には『Bar』がありますよね。
・bartender(バーテンダー)
Bar(酒場)+tend(世話をする)+er(人)→酒場で世話をする人→バーテンダー
お客さんの話を聞いたり、悩み事を相談したりするのが酒場の起源だという訳ですね。
・barrier(障壁)
bar(棒)+er(もの)→棒を置いて相手を邪魔する→障壁
『Bar(横木)』を置いて、相手の侵入を防ぐことから作られた言葉ですね。
・barrel(たる)
bar(横木)+rel(もの)→横木で作ったもの→たる
・embarrass(困らせる)
am(中に)+bar(棒)→中に棒を置く→困らせる
英単語03『bat』
『bat』は本来『打つ』という意味です。
昔、ボールを投げて木の枝で打つ、という遊びがありました。
遊ぶたびに、何か打つものがないかな…。と探していたそうですが、次第にその『打つもの』に名前がついたようです。
それが『バット』です。
他の単語も紹介しておきます。
・batting(打撃)
bat(打つ)+ing(している)→打っている→打撃
・battery(バッテリー)
bat(打つ)+ery(場所)→砲台を打つ場所→放電する場所→二次電池→バッテリー
どうして『打つ場所』が『バッテリー』になったのかというと、昔、戦争をしていた時代では『砲撃する場所』を示していましたが、電気が発明されると共に『放電する場所』と位置づけが変わり、そして、現在では『二次電池』としての役割を持つようになったのです。
・battle(戦う)
bat(打つ)+tle(反復)→反復して打つ→戦う
昔は木の棒を持って、相手を『打っていた』ことが語源になっています。
・debate(討論)
de(下に)+bate(打つ)→相手を下に打つ→会話で打ち負かす→討論
・beat(打ち負かす)
beat(打つ)→相手を打ち負かす
eが途中に入っても同じ意味になります。
英単語04『flower』
みなさんは『flower』という単語を見ると、何を連想するでしょう?
恐らく多くの人は、『花』だと思います。
しかし、この単語もともとは、『栄える』という意味が含まれているのです。
古代の人は『flo(栄える)』ものとは?
という論題に対して、『花』という正解を導き出しているのです。
なので、『flower』は花なのです。
他の単語も紹介しておきます。
・flour(小麦)
flo(栄える)+ur(もの)→栄えた食べ物→主食→小麦
『最良の花の粉』という意味が語源となっているのです。
・floral(花のように美しく)
flor(花)+al(~の)→花のように美しい
・florist(花屋)
flor(花)+ist(人)→花を管理する人→花屋
・flourish(栄える)
flour(花)+ish(~にする)→花は人の心を豊かにする→栄える
『栄える→花→栄える』のように、意味がもとに戻ってきているのです。
英単語05『ball』
『ball(ボール)』といえば、どのようなものを想像するでしょう?
「ボールって、子どもころに遊んでたあの丸い遊具?」という人が多いと思ます。
実はこの単語は『bal,bol(膨れた)』という言葉が語源になっているのです。
空気を入れて膨らむものといえば『遊具のボール』ですよね。
なので、膨れた遊具ということで『ball(ボール)』になったのです。
ballを使った単語を紹介します。
・balloon(風船)
ball(膨れた)+oon(もの)→膨れたもの→風船→気球
・ballot(投票する)
ball(膨れた)+ot(人)→膨れたものを入れる人→ボールを入れる人→投票
「どうして、ボールと関係があるの?」と疑問になると思います。
これは、かつて小さなボールを投票箱に入れて法案の賛否を決めていたことが、名残として残っているのです。
・bold(ボールド体)
bol(膨れた)+d(~させる)→膨れさせる→太字
bol(膨れた)+d(~させる)→膨れさせる→気持ちが大きくなる→思い上がる
パソコンには『ボルード体』というフォントがあります。
これは、簡単に言えば『太字』のことですが、フォントを膨らませていることからそう呼ばれているのです。
この考え方を応用すると、『会話を膨らませる』という意味でも使うことができるのです。
『keep the ball rolling』で、会話や仕事を上手く続けるという意味になります。
『膨らませた状態で転がす』という意味ですね。
つまり、うまく続けるという事になるのです。
・ball(野球の判定)
野球の判定のボールは『unfair ball(アンフェアボール)』の略です。
バッターが打てない玉ということで、『不当な玉』という意味が込められているのです。
英単語06『cap』
『cap』の持つ意味について書いてみたいと思います。
この単語はもともとは『頭、つかむ』という意味があります。
頭にかぶる帽子は『cap(キャップ)』といいますが、帽子は頭にしか使わない事からこの単語が使われています。
他にもいろいろ使われているので紹介します。
・cap(びんのふた)
cap(頭)→びんの頭→びんのふた
・capital(首都)
cap(頭)+tal(~について)→国の頭→首都
・escape(逃げる)
ec(外に)+cape(頭)→頭を外に出す→逃げる
・capacity(容量、能力)
cap(つかむ)+ity(こと)→つかむこと→自分ができること→容量→能力
・captain(キャプテン)
cap(頭)+tain(保つ)→頭を保つ→チームをまとめる→キャプテン
今回は『cap』について書いてみました。
帽子という意味から少し離れて『頭』を意識すると、沢山の英単語に応用できそうですね。
英単語07『car』
自動車の『car』には、もともと『走る』という意味があります。
当時は、走るものといえば『物を運ぶ二輪馬車』のことを指していましたので、現在では自動車のことを『car』と呼んでいるのです。
carは身近なところで沢山使われているので、紹介したいと思います。
・career(経歴)
car(走る)+eer(人)→走る人→人生の痕跡→経歴
経歴が『馬車が通った後のように見える』ことからできた言葉です。
・carry(運ぶ)
car(馬車)+ry(こと)→馬車ですること→運ぶ
『馬車に乗せて運んでいた』ことからできた言葉です。
・charge(請求)
char(馬車)+ge(もの)→馬車に乗せて馬に負担をかけていた→負担→請求
お金をチャージするといいますね。
・carpenter(大工)
car(馬車)+penter(作る人)→馬車を作る人→大工
英単語08『finish』
フランス映画の最後には、『FIN』という文字が現れます。
『これでおしまい』という意味ですが、英語でも色々な場面で使われています。
例えば、『finish(フィニッシュ)』があります。
これは、『fin(終える)』と『ish(~にする)』という言葉が合体したものです。
なので、finishは『終える』という意味になるのです。
finが使われている単語は次のようになります
・finale(終局)
fin(終える)+ale(励まし)→励ましながら終える→終局
・finalist(決戦選の出場者)
fin(終える)+list(帳簿)→最後に帳簿に残っている人→決勝戦の出場者
・fine(元気、天気がよい)
fin(終える)→完成する→元気になる→天気がよい
fin(終える)→完成する→清算する→罰金
・define(定義する)
de(完全に)+fine(限界)→完全な限界を見つける→定義
finには『限界』という意味もあるので、覚えておくと便利です。
・financial(財政上の)
fin(終える)+ance(こと)+ial(~の)→借金を終える→財政上の
最後に『fin』の読み方を確認しておきましょう。
『フィン』と呼んでいる人が多いですが、正解は『ファン』です。
『fine(ファイン)』『final(ファイナル)』『finance(ファイナンス)』と発音することからも想像ができるのではないでしょうか?
ちなみに『Finland(フィンランド)』という国がありますが、『世界の果て、終わり』にあるからという説があります。
諸説ありますので、参考程度にしてください。
今回は『finish』について書いてみました。
正確には『fin』になりますが、探してみると新しい発見があるかもしれませんね。
英単語09『fact』
『fact(ファクト)』はもともと『作る、する』という意味があります。
色々なものを『作ったり』『する』ことで、新しい事実が生まれるので、『実は、事実』という意味になっているのです。
この言葉が使われている単語は、『fax(ファックス)』『fashion(ファッション)』『factory(ファクトリー)』などがあります。
一つずつ説明していきたいと思います。
・facsimile(ファックス)
fac(作る)+simile(同じ)→同じものを作る→送る→ファックス
・fashion(ファッション)
fact(作る)+ion(もの)→新しいものを作る→流行
fact(作る)+ion(もの)→作るという手段→様式、方法
2通りの考え方があります。
・factory(ファクトリー)
fact(作る)+ory(場所)→何かを作る場所→工場
産業革命のことです。
・factor(要因)
fact(作る)+or(もの)→ものづくりは結果をもたらす→要因
・facility(能力)
fac(する)+il(~の)+ity(こと)→できること→能力
英単語10『perfect』
『perfect(パーフェクト)』は『per(完全)』と『fect(する)』が合体した言葉です。
似た言葉にデザート『パフェ』がありますが、あれはフランス語で『完全な』という意味です。
デザートの完全体を『パフェ』と呼んでいるというわけです。
『fect』を使った言葉には、次のようなものがあります。
少し難しいですが、セットで覚えておきたいですね。
・affect(影響を与える)
af(方向)+fect(する)→ある方向にする→影響を与える
・effect(結果)
ef(外へ)+fect(する)→外へ何かをもたらす→結果
・defect(欠陥)
de(否定)+fect(する)→できない事→欠陥
・infect(伝染させる)
in(中に)+fect(する)→中に入る→悪さをする→伝染させる
少し難しい英単語ばかりを扱ってみましたが、完全にイメージで覚えることができるのです。
英検準1級までならイメージだけで取得できます。
ぜひ試してみて下さい。
英単語11『famous』
『famous(フェーマス)』とは、『fa(話す)』と『ous(~な)』が合体した言葉です。
話す内容によって、有名になるというわけです。
『fa』は他の単語にも使われているので紹介します。
・fate(運命)
fa(話す)+te(~にする)→話すことで切り開く→運命
『神の声』が語源になっています。
・fatal(運命的)
fate(運命)+al(~な)→運命的な
話す内容によって、運命的な出会いがあるかもしれませんね。
・fable(寓話)
fa(話す)+ble(~された)→話され続けてきたこと→昔話→寓話
桃太郎やさるかに合戦など、昔の人が話が話した物語のことを寓話(ぐうわ)といいますね。
・fairy(妖精)
fa(話す)+iry(場所)→伝説で話された場所→伝説で出てくるもの→妖精
昔の人は『妖精』と考えていたのです。
・infant(幼児)
in(~でない)+fa(話す)+ant(人)→話せない人→幼児
英単語12『port』
『port(ポート)』は『運ぶ』という意味です。
何かを運ぶときに、この単語を使います。
運ぶ場所といえば『港』ですね。
パソコンのポートは、『扉』という意味ですね。
データを運ぶときに通る扉ということです。
どのように使われているのか紹介していきましょう。
・portable(持ち運び可能)
port(運ぶ)+able(可能)→運ぶことができる→持ち運び可能
・airport(空港)
air(飛行機)+port(港)→空港
・import(輸入)
im(中に)+port(運ぶ)→国内に運ぶ→輸入
・support(支持する)
sup(下)+port(運ぶ)→自分の下で運ぶ→自分のために働く→支持する
・report(報告)
re(元に)+port(運ぶ)→状況を整理して発信元に返す→報告
・important(重要)
im(中に)+port(運ぶ)+ant(~な)→自分の中に運ぶ→重要
英単語13『farm』
『farm(ファーム)』は『しっかりした』という意味です。
地代をしっかりと支払っていた場所が『農場』や『農園』だったという訳です。
野球で二軍のことを『ファーム』といいますが、これは選手をしっかりと育成する場だからです。
farmが使われている単語を紹介します。
・farmer(農場主)
farm(農場)+er(人)→農場の人→農場主
・firm(会社)
farm≒firm→しっかりとした→会社
・affirm(主張する)
af(~を)+firm(しっかりとした)→しっかりした事をいう→主張する
・confirm(確認する)
con(完全に)+firm(しっかりとした)→完全にりっかりとする→確認する
・reconfirm(再確認する)
re(再び)+confirm(確認する)→再確認する
英単語14『fly』
fly(フライ)には『飛ぶ』という意味です。
これは、fl(飛ぶ)+y(こと)→飛ぶもの→ハエのようになります。
また、flには『流れる』という意味もありますので、紹介していきます。
・dragonfly(トンボ)
dragon(ドラゴン)+fly(飛ぶもの)→トンボ
・firefly(ホタル)
fire(火)+fly(飛ぶもの)→ホタル
・butterfly(蝶)
butter(バター)+fly(飛ぶもの)→蝶
魔女が蝶に変装してバターを盗み食いしたという迷信があります。
・flight(飛行)
fl(飛ぶ)+ght(こと)→飛行
・flow(流れ)
fl(流れる)→流れ
・flood(洪水)
fl(流れる)+ood(こと)→洪水
・influence(影響を与える)
in(中に)+flu(流れる)+ence(こと)→中に流れてくること→影響を与える
・influencer(影響を与える者)
influence(影響)+er(人)→影響を与える者→インフルエンサー
英単語15『fund』
fund(ファンド)は『底』という意味です。
○○ファンドという金融会社がありますが、これは会社の基盤となるという意味なのです。
どのように使われているのか紹介していきましょう。
・foundation(基礎、根拠)
found(底)+ation(~にする)→底にする→基礎→根拠
化粧の基礎になる下地クリームのことを、ファンデーションといいますね。
・fundamental(基本的な)
fund(底)+ment(こと)+al(~の)→底にあること→基本的な
・profound(奥深い)
pro(前に)+found(底)→底が手前にある→奥深い
・refundable(払い戻し)
re(再び)+fund(資金)+able(できる)→資金を返すことができる→払い戻し
英単語16『stewardess』
stewardessは『豚小屋の女性の番人』という意味です。
sty(豚小屋)+ward(見る)+ess(女性)→stewardess(スチュワーデス)です。
アメリカでは女性差別用語なので、flight attendant(客室乗務員)と呼ばれています。
ここでは、ward(見る)が使われている単語を紹介します。
・steward(執事)
sty(豚小屋)+ward(見る)→豚小屋を監視する人→世話役→執事
・award(賞)
a(~を)+ward(見る)→よく観察する→研究熱心→賞
・aware(気づいている)
a(~を)+ware(見る)→気づく→気づいている
・beware(注意する)
be(完全に)+ware(見る)→しっかり見る→注意する
・reward(報酬)
re(完全に)+ward(見る)→手伝い→報酬
英単語17『know』
knowは『知る』という意味です。
この単語、実はnote(ノート)と語源が同じなのです。
note(印)→書き記す→知る→know(※語尾の省略)
ここでは、『知る』という言葉が使われている単語を紹介します。
・knowledge(知識)
know(知る)+ledge(こと)→知っていること→知識
・notice(通知)
not(知る)+ice(こと)→知ること→通知
・notion(概念)
not(知る)+ion(こと)→知ること→概念
・ignore(無視)
ig(~でない)+nore(知る)→知らない→興味がない→無視
・recognize(認識する)
re(再び)+co(一緒に)+gn(知る)+ize(~にする)→再び一緒に知る→認識する
英単語18 『grade』
gradeは『階段』という意味です。
階段→段階→成績→等級
階段を上る→成績をつける→等級に分ける
のように意味が発展しています。
ここでは、gradeが使われていている単語を紹介します。
・upgrade(性能が上がる)
up(上に)+grade(階段)→階段を上る→等級が上がる→性能が上がる
・gradation(推移)
grade(階段)+ate(~にする)→階段状→段階的→推移
・graduate(卒業する)
grade(階段)+ate(~にする)→階段にする→段階を経る→卒業する
・gradually(徐々に)
grade(階段)+al(~の)+ly(~に)→段階的に→徐々に
英単語19『digest』
digestは『要約』という意味です。
ダイジェスト版という言葉がありますが、あれは要約版という意味です。
di(離れて)+gest(運ぶ)→食べ物がバラバラに運ばれる→消化する→一定のところにまとまる→要約
digestは動詞で消化するという意味です。
ここでは、gestを使った単語を紹介します。
・gesture(意思表示)
gest(運ぶ)+ure(こと)→意志を言葉で運ぶ→身振り手振り→意思表示
・register(登録)
re(元へ)+gister(運ぶ)→元の場所へ運ぶ→所在を明らかにする→登録
・suggest(提案)
su(下に)+gest(運ぶ)→下に運び出す→様子を伺う→提案
・congestion(混雑)
con(共に)+gest(運ぶ)+ion(こと)→共に運ぶ→同じ場所に集まる→混雑
・exaggerate(強調)
exa(外へ)+ger(運ぶ)+ate(~にする)→外へ運ぶ→枠からはみ出す→強調
英単語20 『visit』
visitは『訪問する』です。
vis(見る)+it(行く)→見に行く→訪問する
ここでは、it(行く)が使われている単語を書いてみたいと思います。
・initial(頭文字)
in(中に)+it(行く)+ial(~の)→はじめて中に入る→初め→頭文字(イニシャル)
・exit(出口)
ex(外に)+it(行く)→外に行く場所→出口
・orbit(軌道)
orb(球)+it(行く)→地球を回る→軌道
・transit(通過)
trans(越える)+it(行く)→越えていく→通過
・ambitious(野心的な)
amb(周囲)+it(行く)+ous(~な)→周囲で選挙の票を集めに行く→野心的な
➌ a, an, theの違い
a, an, theは冠詞と呼ばれ,「範囲をしぼる」役割があります。a, anはもともとoneからできています。つまり,「1つのもの」です。the はもともとthis, thatなどからできているので「特定できるもの」ということになります。
(1) aとanの違い
両方ともoneが起源なので「特定できない1つのもの」と考えてください。後にある名詞が母音から発音するのであればan,子音から発音するのであればaをつけます。母音とは『a, i, u, e, o』のこと、子音とはそれ以外の音のことです。
(2) a, anとtheの違い
theはthis, that, these, thoseが起源なので,「これ」「あれ」「これら」「あれら」などのように「特定できるもの」と考えてください。
例文紹介
① I want a knife. (私はナイフがほしい。)
▶ナイフであればどれでも構いません。
***
② I want the knife. (私はそのナイフがほしい。)
▶決まったナイフでなければなりません。
***
③ I want knives. (私はナイフがほしい。)
▶ナイフであればどれでも構いません。
***
④ I want the knives. (私はそのナイフが欲しい。)
▶特定できるいくつかのナイフが欲しい。
▶a, anはone(1つ), theはthis, that, these, thoseを表しているので,限定できるものに使われます。
***
⑤ I have a cat. The cat is black.
(私は猫を飼っています。その猫は黒いです。)
▶前に猫の紹介をしているので,どの猫の話をしているかを特定できます。
***
⑥ Open the window. (窓を開けなさい。)
▶どの窓を開けるのかが特定できているということです。
***
⑦ The earth arounds the sun. (地球は太陽の周りをまわっている。)
▶地球や太陽は誰もが特定できます。
***
⑧ Mt. Fuji is the highest mountain in Japan.
(富士山は日本でいちばん高い山です。)
▶最も高い(最上級)ということは特定できます。
***
⑨ The dog is a faithful animals. (犬は忠実な動物である。)
▶ 犬という動物を特定できます。
***
⑩ I get up at seven in the morning. (私は朝7時に起きます。)
▶ 朝は誰もが特定できます。
➍疑問詞疑問文
誰のこと?何をするの?どこなの?など、Yes、noでは返事ができない文の事を疑問詞疑問文といいます。中学生で習う疑問詞には次の8種類があります。
(1) who(誰が)
(2) what(何を)
(3) where(どこで)
(4) when(いつ)
(5) why(なぜ)
(6) which(どちら)
(7) whose(誰のもの)
(8) how(どのように)
✅疑問詞疑問文の作り方
次のいずれかの形になります。
(1) 疑問詞+疑問文
(2) 疑問詞+名詞+疑問文
(3) 疑問詞が主語になるときは、疑問詞+動詞+その他の語
例文紹介
① Who is he? (彼は誰ですか。)
▶『(1)疑問詞+疑問文』を利用しています。この場合、疑問詞はwho、疑問文はis heになります。
***
② Who plays tennis? (誰がテニスをしますか。)
▶『(3)疑問詞が主語になるときは、疑問詞+動詞+その他の語』を利用しています。この場合、誰=whoが主語になるので、このルールを利用します。また、whoは三人称単数として扱うため、動詞はplaysとします。
***
③ What does he study? (彼は何を勉強しますか。)
▶『(1)疑問詞+疑問文』を利用します。この場合、疑問詞はwhat、疑問文はdoes he studyになります。
***
④ What time do you get up? (あなたは何時に起きますか。)
▶『(2)疑問詞+名詞+疑問文』を利用します。この場合、疑問詞はwhat、名詞はtime、疑問文はdo you get up?になります。時間を聞きたいときはWhat time、『起きる=get up』を利用します。
▶現在形で何時に起きるのか?と質問した場合、『習慣』を表します。ですので、『あなたはふつういつも何時に起きますか?』という意味になります。
***
⑤ What day is it today? / It's Friday.
(今日は何曜日ですか。-金曜日です。)
▶『(2)疑問詞+名詞+疑問文』を利用します。曜日を聞くときはWhat dayとします。
▶時間、曜日、日付など、主語が存在しない場合は『it』を補っておきます。
***
⑥ Where do you play tennis? / I play tennis in the park.
(あなたはどこでテニスをしますか。-公園でします。)
▶『(1)疑問詞+疑問文』を利用します。この場合、疑問詞はwhere、疑問文はdo you play tennis?になります。
▶『あなたは…?』と質問されているので、答えるときは『わたしは…』とします。
▶『in=空間内』を表します。詳しくは後々説明をします。また、公園というのは一般的に共通認識のあるものですので『the park』とします。
***
⑦ When do they play tennis? / They play tennis after school.
(彼らはいつテニスをしますか。-彼らはテニスを放課後にします。)
▶『(1)疑問詞+疑問文』を利用します。この場合、疑問詞はwhen、疑問文はdo they play tennis?になります。
▶『after=後ろ(時間)』を表します。『after school=学校が終わった後=放課後』と解釈します。
▶Theyには3つの意味があります。『彼ら、彼女ら、それら』この3人衆はセットで覚えておくようにします。三人称単数ではないので、動詞にsはつけません。
***
⑧ Why do you want a camera?
(あなたはなぜカメラがほしいのですか。)
▶『(1)疑問詞+疑問文』を利用します。この場合、疑問詞はwhy、疑問文はdo you want a camera?になります。
▶『want=欲する』という一般動詞です。
▶a cameraとなっているということは、カメラならどのようなものでもよいという意味になっています。
▶『why-because』はセットで使う事があります。『なぜ…?なぜならば…』という具合です。
Because I like cameras. (なぜなら、私はカメラが好きだからです。)
▶camerasと複数形になっているのは、一般的にカメラが好きだという意味になります。
***
⑨ Which desk is yours? / This is mine.
(どちらがあなたの机ですか。-こちらが私の机です。)
▶『(2)疑問詞+名詞+疑問文』を利用します。この場合、疑問詞はwhich、名詞はdesk、疑問文はis yoursになります。
▶『yours=あなたのもの』『mine=私のもの』という意味です。
▶『(1)疑問詞+疑問文』を利用して書き変えることができます。
Which is your desk? (どちらがあなたの机ですか。)
どちらも同じ意味になります。
***
⑩ Whose car is this? / It's my father's car.
(これはだれの車ですか。-私の父の車です。)
▶『(2)疑問詞+名詞+疑問文』を利用します。この場合、疑問詞はwhose、名詞はcar、疑問文はis thisになります。
▶『my father's=私の父のもの』になります。
▶『(1)疑問詞+疑問文』を利用して書き変えることができます。
Whose is this car? (この車はだれのものですか。)
どちらのパターンも意味は同じになります。
***
⑪ How are you? / I'm fine.
(ごきげんいかがですか。-元気です。)
▶『(1)疑問詞+疑問文』を利用しています。この場合、疑問詞はHow、疑問文はare youになります。
▶be動詞は『存在』を表すことから,『あなたはどのように(存在)していますか?=ごきげんいかがですか?』となります。
***
⑫ How do you go home? / I go home by car.
(あなたはどのようにして帰宅しますか。-車で帰宅します。)
▶『(1)疑問詞+疑問文』を利用しています。この場合、疑問詞はHow、疑問文はdo you go homeになります。
▶『home=家に』という意味なので、go to the homeにはなりません。詳しくは後々紹介します。
▶『by=すぐそば』という意味です。車で移動するという事は、車は自分のすぐそばにあるという事を意味しています。通常、交通手段を表すときは『by』を使います。
▶homeとhouseの違い
homeは家庭を、houseは建物自体を表します。つまり、homeは温かいイメージ、houseは無機質なイメージになります。houseはモノですが、homeはモノではないため、数えることができないのです。
例文1 She goes her home. (彼女は自分の家に帰る。)
例文2 She goes to the house. (彼女はその建物に向かう。)
***
⑬ How many brothers do you have? / I have two (brothers).
(あなたには兄弟が何人いますか。-2人います。)
▶『(2)疑問詞+名詞+疑問文』を利用しています。この場合、疑問詞はHow、名詞はmany brothers、疑問文はdo you haveになります。
▶数をたずねるには、『How many+ 複数名詞+疑問文』を利用します。
▶manyとmuchの違い
manyは『数』、muchは『量や程度』を表します。
例文1 How many apples do you have?
(あなたはりんごを何個持っていますか。)
例文2 How much do you pay?
(あなたはいくら支払いますか。)
➎助動詞
助動詞とは,be動詞や一般動詞を補助する言葉です。中学校で習う助動詞の種類をまとめておきます。
このラインより上のエリアが無料で表示されます。
(1) will (100%の可能性)『未来』必ず~する
(2) must(100%の可能性)『義務』~しなければならない
(3) can(70%の可能性)『可能』~できる
(4) may(50%の可能性)『予定』~かもしれない
(5) shall willの古語のような言葉
助動詞を使うには次のルールがあるので,覚えておきましょう。
✅助動詞の文の作り方
(1) 助動詞+動詞の原形
(2) 助動詞を中心にして文が作られている
例文紹介
※V原…動詞の原形
① I can run fast. (私は速く走ることができます。)
▶canは70%の可能性を表す
▶can V原=『V原できる』になります。動詞を補助する言葉を助動詞といいます。助動詞があるときは、助動詞を優先して文を作ります。
***
② Jane is able to play the piano.
(ジェーンはピアノをひくことができます。)
▶助動詞canはbe動詞を使って書きかえることができます。
▶『can=be able to V原』とすることができます。
***
③ Yuri cannot play the piano.
(ユリはピアノをひくことができません。)
▶助動詞の否定文は,助動詞にnotをつけます。
▶助動詞canがあるので,canを優先に文を作ります。
▶canの否定文は『can not=cannot=can't』とすることができます。
***
④ He is not able to drive a car.
(彼は車を運転することができません。)
▶be動詞を使った文はbe動詞主導で文を作ります。
▶『can=be able to V原』を利用しています。
***
⑤ Can you speak French? / Yes, I can. No, I can't.
(あなたはフランス語を話すことができますか。
-はい,できます。いいえ,できません。)
▶助動詞の疑問文は,疑問文を文頭に持ってくる。
助動詞の文は助動詞でこたえる。
▶助動詞canがあるので,can主導で文を作ります。
疑問文は、canを主語の前に出します。助動詞canで質問されたら、canでこたえます。
▶『speak=話す』は動作を表す一般動詞です。
***
⑥ Who can make a cake?
(だれがケーキを作ることができますか。)
▶whoが主語になるときは,『疑問詞+普通の文 』の語順になる。
▶『make=作る』は動作を表す一般動詞です。
***
⑦ Can I open the window? / Sure. Sorry, you can't.
(窓を開けてもいいですか。
-いいですよ。ごめんなさい,いけません。)
▶許可を求めるときは『Can I~?』を使います。
▶『私は窓を開けることができますか?』=『窓を開けてもいいですか?』と考えます。
***
⑧ Can we visit you now? / OK. I'm sorry. I'm busy now.
(今,あなたを訪れてもいいですか。
わかりました。ごめんなさい,今,忙しいのです。)
▶許可を求める表現です。
▶『私たちはあなたを訪れることができますか?』=『あなたを訪れてもいいですか?』と考えます。
▶visit=『訪れる』は動作を表す一般動詞です。
***
⑨ Can you help me? / All right. I'm sorry, I can't.
(私を手伝ってくれますか。
-わかりました。ごめんなさい,できません。)
▶依頼をするときの表現です。
▶『あなたは私を助けることができますか?』=『助けてくれませんか?』と考えます。
▶help=『助ける』は動作を表す一般動詞です。
***
⑩ I must wash the dishes.
(私は皿を洗わなければなりません。)
▶mustは100%の可能性を表す
▶mustは『~しなければならない』という助動詞なので、『助動詞+V原』となります。
***
⑪ You must not sleep in the library.
(図書館で寝てはいけません。)
▶mustの否定は強い禁止
▶『must not=mustn’t』と表すこともできます。
***
⑫ Must I do the job?
(わたしはその仕事をしなければなりませんか。)
▶助動詞を文頭にすると疑問文になります。
▶仕事をするというのは『do』を使って表すことができます。
***
⑬ He must be sick.
(彼は病気に違いありません。)
▶mustは可能性100%を表します
▶must beで『違いない』。sick=病気。
***
⑭ We have to go there.
(わたしたちはそこへ行かなければなりません。)
▶must+V原=have to V原
▶そこへは『there』を使います。
***
⑮ You may come here.
(あなたはここに来てもいいですよ。)
▶mayは50%の可能性を表す
▶mayには『~してもよい』『~かもしれない』という意味があります。
▶助動詞ですので『may+V原』となります。
***
⑯ You may not eat this cake.
(あなたはこのケーキを食べてはいけません。)
▶mayの否定は禁止になります。
▶may notよりもmust notの方が強い禁止を表します。
***
⑰ May I use this pen?―Yes, you may. / No, you may not.
(このペンを使ってもいいですか。
―はい,いいですよ。いいえ,いけません。)
▶mayは疑問で許可を求めます。
▶May I~?で『私が~してもよいか?』という文になります。
▶答えるときはmayを使います。
***
⑱ She may be busy.
(彼女は忙しいかもしれません。)
▶mayは可能性50%を表します。
▶busyは『忙しい』という形容詞ですので、be動詞が必要になります。
***
⑲ Will you open the door?
(ドアを開けてくれませんか。)
▶will you~は確実性の高い依頼や勧誘を表します。
▶Willは可能性100%の助動詞です。つまり、Will you~で依頼や勧誘をする場合、確実性の高いものを指すことになります。
***
⑳ Shall I help you?
(お手伝いしましょうか。)
▶shallはwillの古語のようなことばです。
▶shall I~?で『私が~しましょうか?』、shall we~で『一緒に~しましょう』という意味になります。
▶shall we~?=Let's~になります。
➏命令文
命令文とは『~しなさい』というように,相手に指示するときに使う文です。相手に指示するという事は、『あなたは…すべきだ』という意味が含まれているため主語は『You』となります。しかし、主語を書いてしまうと、通常の文と区別が使いないため省略しているというわけです。命令文の種類は次の通りになります。
(1) 肯定の命令文
V~.
(2) 丁寧な命令文
Please V~.
(3) 禁止の命令文
Don't V~.
(4) 勧誘の命令文
Let's V~.
例文紹介
① Study English every day.
(毎日英語の勉強をしなさい。)
▶動詞から始まる文を『命令文』といい『~しなさい』という意味になります。
▶勉強するという動作は一般動詞『study』を使い,Aを勉強する=『study A』とします。
▶『every day=毎日』
▶英語は相手に伝えたいことを順に並べていく言語だと思ってください。
動詞から始るということは,相手に強く伝えたい言い方だということです。
***
② Be quiet in the library.
(図書館では静かにしましょう。)
▶be動詞から始めることもできます。『quiet=静かに』のように形容詞を使いたい場合はbe動詞を利用します。
▶inは『内部』を表す前置詞です。
▶the は『共通認識』を表します。つまり、普通図書館では静かにするでしょ?という意味があります。
***
③ Please open the window.
(どうぞ窓を開けてください。)
▶丁寧に相手に伝えたいとき,命令文に『please』をつけますが,次の2通りのつけ方があります。
・その1[文の先頭につける] Please open the window.のようになります。
・その2[文の最後につける] Open the window, please.のようになります。
文の最後につける場合はふつう『カンマ(,)』をつけます。
▶開けるという動作は一般動詞『open』を使い,『Aを開ける=open A』とします。
***
④ Don't sit down.
(すわってはいけません。)
▶禁止行為を相手に伝えたいとき,命令文に『Don't 』を文の先頭につけます。
▶座るという動作は一般動詞『sit 』を使います。
▶ふつう座るとは,下に座ることから『 sit down 』で座ることを表します。
***
⑤ Don't be late for school.
(学校に遅れてはいけません。)
▶be動詞を使った文でもDon'tを使って否定を表します。
▶『late=遅い』という形容詞ですので,be動詞が必要になります。
▶『be late for A=Aに遅れる』で覚えておきましょう。
***
⑥ 放課後,野球をしましょう。
(Let's play baseball after school.)
▶相手を誘いたいとき,命令文に『 Let's 』を文の先頭につけます。
▶放課後は学校が終わった後の時間のことを指すことから,後という意味を持つ前置詞『 after 』を使って『 after school 』とします。
▶Let'sは『Let us』の省略形ですが、今は深く考えないでください。
➐進行形
進行形というのは『その時の動作』のことを指します。間違いやすいのは現在形と現在進行形です。現在形とは『習慣、事実』を表してものですので、決してその時の動作を表している訳ではないのです。例えば、次の例文を見てみましょう。
例)He goes to school everyday.
(彼は毎日学校へ行きます。)
この文の場合、毎日学校へ行くという『習慣』を表しているに過ぎません。今、学校へ行っている訳ではないのです。では、その時の動作を表すにはどのようにすればよいのしょう?英語でその時の動作を表す言葉を『進行形』と呼びます。進行形は『beV+Ving』で表します。beVを利用していることから、進行形はbeVの文だという事になります。つまり、beV主導で文が動くことになります。
例文紹介
※Vは動詞を表します。Vingは動詞のing形です。
① I am writing a letter now.
(私は今,手紙を書いています。)
▶進行形は『beV+Ving』です。
▶書く=『write』は動作を表す一般動詞ですが,動詞にingがつくと動詞ではない形になります。この文の動詞は『am(be動詞)』です。
▶write+ing ⇨ 『writing=書くこと』となります。
このように,一般動詞ingは動詞としての役割がなくなります。進行形は『be動詞の文』だということを理解してください。
***
② Mr. Ikeda is teaching English now.
(池田先生は今,英語を教えています。)
▶進行形=『beV+Ving』です。
▶Mr.Ikeda=『He』と考えて,be動詞『is』を使います。
***
③ Nancy knows my sister.
(ナンシーは私の姉を知っています。)
▶知っている=『know』のように,『状態』を表す一般動詞は進行形にしません。
***
④ He isn't reading a book.
(彼は本を読んでいません。)
▶進行形はbe動詞の文なので,否定文にするには『be動詞』を否定(is not=isn't)にします。
***
⑤ Are you speaking English now? / Yes, I am. No, I'm not.
(あなたは今,英語を話していますか。
-はい,話しています。いいえ,話していません。)
▶進行形はbe動詞の文なので,疑問文にするにはbe動詞を『主語の前』に出します。
▶答えるときは、be動詞で答えます。
***
⑥ What are you doing now? / I'm listening to the radio.
(あなたは今,何をしていますか。-私はラジオを聞いています。)
▶『疑問詞+疑問文』です。do=『する』は動作を表す一般動詞です。
▶一般動詞の文の先頭に置いたり否定文で使うdoは助動詞です。区別をしておきましょう。
***
⑦ Ken was cooking then.
(健はその時料理をしていました。)
▶beVが過去形になると、過去進行形になります。
▶『then=そのとき』で過去を表す言葉です。
***
⑧ They were running in the park yesterday.
(彼らは昨日公園で走っていました)。
▶beVが過去形なので過去進行形の文です。
▶『yesterday=昨日』で過去を表す言葉です。
▶runは進行形になると、runningのようにnを重ねて書きます。同じように重ねて書くものとして、swim ⇨ swimmingなどがあります。
⑨ What were you doing yesterday morning?
(あなたは昨日の朝何をしていましたか?)
▶『yesterday morning=昨日の朝』で過去を表す言葉です。
▶『疑問詞+疑問文』の形です。
➑There is(are)~
聞き手にとって、『初めての情報を伝えるとき』に利用する英文です。この英文の性質として、thereには「そこ」という意味が存在しないということです。ただの飾りのようなものだと考えてください。また、主語は「~」の部分になります。さらに、聞き手にとって初めての情報を表すので、「the」「my」「this」などの『共通認識』を表す言葉を主語に持ってくることはできないのです。主語が単数であれば「is」、複数であれば「are」を利用します。これらの事をまとめると次のようになります。
このラインより上のエリアが無料で表示されます。
▶要点の整理
① There is(are)~.の主語は「~」の部分。
② 主語が単数ならis、複数ならareを使う。
③ 新情報を表すので、主語に「the, my, that」など共通認識を表す言葉は使う事ができない。
ここで、理解しておかなければならないのは、「a, an, the」の違いになります。aと anは「one」が語源になるので、「特定できない1つのもの」という意味があります。つまり、新しい情報だということになります。しかし、the(それ)は「this(これ)やthat(あれ)など」が語源になるので、「特定できるもの」という意味になるのです。つまり、すでに知っている情報だということになります。
つまり、there is(are)~.の文では、the, this, that, myなどは特定できてしまうので、使う事ができないのです。
例文紹介
① There is a book on the desk.
(机の上に本があります。)
▶There is(are)~.は、「始めてみる情報」ときに用いる文ですので、theやmyなどを使った「共通認識ができる語句」があるときには使えません。
▶主語は「a book」です。
▶「A book is on the desk.」としてもほぼ同じ意味になります。
There を使う事で、これから新情報を伝えるよ!というサインになっているのです。
✖ There is my book.
(わたしの本だということが分かってしまっている。)
○ There is a book.
(1冊の本だというだけで、どの本なのかは分かっていない。)
② There were not (weren't) any cats on the chair.
(いすの上にネコはいませんでした。)
▶複数ある場合は、areを用います。この場合、過去形になっているのでwereになっています。not anyで全くないという意味になりますが、その後が複数形になっていることに注意しましょう。英語では『全くない』は複数扱いなのです。
▶There is(are)~.の文はbe動詞が主導になっています。ですので、be動詞を否定にすればよいです。
③ Are there any apples in the box? Yes, there are. / No, there aren't.
(箱の中にりんごがありますか。
―はい,あります。いいえ,ありません。)
▶There is(are)~.の文はbe動詞を使った文なので、be動詞を先頭に移動することで疑問文にできます。
▶答えるときは、there is(are).とします。
▶「いくつかの」というのはsome(肯定文)、any(疑問文、否定文)で利用します。厳密には、肯定を求めるときにはsomeを、返事がハッキリしないような場合にはanyを利用します。
④ How many pictures are there in the box? There are five pictures.
(箱の中に写真が何枚ありますか。)
▶数をたずねるときは、『How many +複数名詞+疑問文』を利用します。
➒前置詞
前置詞とは,単語の前に置いて説明を加える言葉のことです。今回はto, for, fromについて学習します。この3つの前置詞はセットにして覚えとくと理解しやすいですので、それぞれどのような特徴があるのかを整理しながら覚えていきましょう。
① to ➡ 未来志向

toは『点に向かって進み必ず相手に届く』というイメージです。ゴールを中心に考えているのが大きな特徴です。次の例文を見てみましょう。
例文1 I go to Canada.
(私はカナダへ行きます。)
▶確実にカナダへ行くことを表しています。
例文2 Fly to Tokyo
(東京行きのフライト)
▶確実に東京へ行くことを表しています。
例文3 Five to seven
(7時5分前=6時55分)
▶7時というゴールから戻ってきています。
ここで、toと相性が良い一般動詞を紹介しておきます。
(1) Send(送る)
(2) Speak(話す)
(3) Teach(教える)
(4) Sell(売る)
(5) Explain(説明する)
(6) Give(与える)
toは必ず相手に届くという性質を持っているため、『相手がいないと動作が成り立たない』という事になるのです。つまり、このような一般動詞の場合、必ず相手に届くtoを使います。
例文4 I teach English to students.
(私は生徒に英語を教えています。)
▶教えているという事実を伝えています。
例文5 She sent the gift to her grandfather.
(彼女は祖父にプレゼントを送った。)
▶すでにプレゼントは相手に届いているという事を表しています。
例文6 I’ll give this book to you.
(私はこの本をあなたにあげます。)
▶確実にあなたにあげるという事を伝えようとしています。
例文7 Can you explain the rule to me?
(その規則を私に説明してくれますか。)
▶その規則を確実にわたしに教えてほしいという要求をしています。
※注意点 動詞の直後に人を置くとToは省略されます!
例文5’ She sent her grandfather the gift.
例文6’ I’ll give you this book.
例文7’ Can you explain me the rule?
動詞+モノ+to人
動詞+人+モノ
の形を覚えておくと便利です。
② for ➡ 意識の向く先

『面に向かって進んでいるが,まだ届いていない』というイメージです。 スタートを中心に考えているのが大きな特徴です。
例文1 I’ll leave for Osaka.
(私は大坂方面へ出発します。)
▶leaveは『離れる』という動詞であるため,スタート地点を中心に考えなければなりません。よって、forを使います。
例文2 Exercising is good for our health.
(運動は私たちの健康によいです。)
▶『健康』になることがゴールです。つまり、まだゴールには届いていないのです。よって、forを使います。
例文3 I have a present for you.
(あなたにプレゼントがあります。)
▶『プレゼントはあるけれど,まだ相手に届いていない。』という状態を表します。
③ from ➡ 離れる
toとは反対に,『起点から離れていく』のがfromのイメージです。
例文1 I am from Tokyo.
(私は東京の出身です。)
▶東京という起点から離れています。
例文2 We were waiting from 11:00.
(私たちは11時から待っています)
▶11:00という起点から離れています。11:00に待ち合わせでもしていたのでしょうか…。
例文3 How far is it from here to the post office?
(ここから郵便局までどのくらい遠いですか。)
▶How farは距離を聞くときに使います。
▶主語がない場合、形式的に主語をitにします。
▶『ここ』という起点から離れています。
▶toが使われているので、確実に郵便局に行きたいことが分かります。
『from A to B』で『AからBまで』という意味になります。
■ to, for, fromのイメージ

➓前置詞up,down,in,on,at,off
今回は前置詞up,down,in,on,at,offについて学習します。それぞれの違いに気をつけながら核となる意味を理解していきましょう。前置詞の意味を理解せずに熟語で暗記していると、必ず限界がきていしまいます。どうしてその熟語の意味がそうなのかということを前置詞の立場から理解していくと、英語の勉強はかなり楽になります。勉強は頭の善し悪しではなく、要領です。
① Up ➡ 上に向かう
upは『上の方に向かっている』または『起点となるポイントより上の状態』というイメージがあります。
『目覚める』という意味の『wake』に対して、get upは『実際に起き上がる』という動作に近いイメージだといえます。また、move up(昇進する)は、現在よりも上の地位に上がることを示すことになります。
例文1 He gets up at six.
(彼は6時に起きます。)
▶実際に起き上がって、支度をするという意味です。
例文2 The monkey climbs up a tree.
(そのサルは木に登る。)
▶climbは『のぼる』という一般動詞のことです。
▶木に登って『上の方に上がっていく』というイメージです。
② Down ➡ 下に向かう
upの反対語だと思って下さい。『下の方に下がっている』『起点となるポイントよりも下の状態』というイメージです。
車を降りる際は『get out』が使われるのに対し、バスのような高い乗り物から降りる場合は『get down』を使います。その他に、be down(床に伏せる)、feel down(気分が落ち込む)などの表現があります。
例文1 She will get down the bus soon.
(彼女は間もなくそのバスをおりるでしょう。)
▶乗り物の乗り降りは『get』を使います。バスから降りるときは、通常高いところから低いところへ移動するので『down』を利用します。
③ In ➡ 限られた空間の中
inは『空間的な広がりのある環境の中にいる』というイメージです。
in the world(世界で)からin the box(箱の中)まで、大小に関わらず空間の内部を示すほか、in tears(涙ながらに)やin the rain(雨の中)、in black(喪服を着た)のように、そのものの中に自分の身を置くような状態も表します。
例文1 There are some apples in the box.
(その箱の中には、りんごがいくつかあります。)
▶some(いくつかの)は肯定文、anyは否定文と疑問文で利用します。
▶the boxという限られた空間内にりんごがある事を表しています。
例文2 The balloon will go up in the sky.
(その風船は空に上がっていくでしょう。)
▶空全体という限られた空間内に移動するという事を表しています。
例文3 Birds are singing up in the tree.
(小鳥たちが木の上でないている。)
▶木という限られた空間内で鳴いているという事を表しています。
④On ➡ 接触
空間を表すinに対して、onは『平面的な部分に接触している』というイメージです。
on the table(テーブルに)やon the wall(壁に)などの物理的な接触のほか、季節や年などの長い期間を表すinとは違い、on Friday(金曜日に)のようにカレンダー上のあるポイントを表す場合にも使われます。
例文1 The cat is on the sofa.
(そのねこは、ソファーの上にいます。)
▶ソファ―に接触しているという事は、ソファーの上にいるという事です。
例文2 There is a clock on the wall.
(壁に時計が一つかけてある。)
▶壁に接触しているということは、壁にかかっているという事です。
例文3 Mike plays tennis on Sunday.
(マイクは日曜日にテニスをします。)
▶曜日というのは、どの月でも必ずあります。つまり、カレンダーの上に必ず接触しているものです。月単位のカレンダーが多くありますが、これでは全ての月が一つのカレンダー上にあるとは言えません。なので,月を表すときは範囲を表す『in』を利用するのです。
⑤At ➡ 点
atは『ある一点』を表します。つまり、ちょうどその時、ちょうどその場所でというものです。例えば、at3:00は『3時ちょうど』、 at stationは『地図上でのはっきりした場所』です。inは特定の空間、onは平面を表すのに対して、atは『ある一点』を表すイメージなのです。
at 3:00(3時に)のように1日のうちのごく短い時間を指す場合や、at station(駅で)のように地図上のある一点を示す場合に使われます。また、sit at table(テーブルに着く)、at 5 page(5ページに)、at exit(出口で)のように使うことができます。
⑥Off ➡ 離れる
offには『もともとあった場所から離れる』という、onとは反対のイメージがあります。
be off(去る)のように人がその場から離れる場合のほか、get off the car(車を降りる)のように人が何かから離れる場合や、take off the socks(靴下を脱ぐ)のように物が自分から離れる場合などに使われます。
⓫前置詞 around, among, between, during, for
今回は前置詞 around, among, between, during, forについて学びましょう。非常に紛らわしい前置詞シリーズです。囲むのか囲まれるのか、どのように囲まれているのか、期間なのかその時間なのか?非常に区別が難しい前置詞たちです。必ずこの5つの前置詞はセットにして覚えておきましょう。
① around ➡ 囲む
『何かを取り囲んでいる状態』がaroundのイメージです。
around the tree(木の周り)のように、場所を取り囲む場合に使われます。
例文1 There are five lakes around Mt. Fuji.
(富士山の周りには5つの湖がある。)
▶around Mt. Fujiで『富士山の周りに』という意味です。
▶lakeは湖
例文2 The dog goes around the tree.
(その犬は木の周りをぐるぐる回ります。)
▶around the treeで『木の周り』という意味です。
② among ➡ 不特定のものに囲まれる
aroundの逆に、「何かに取り囲まれている状態」がamongのイメージです。
対象のものが『特定できないもの』の場合に使われることから、among the treeという場合は不特定の多くの木に囲まれていることを表します。
例文1 My house is among the trees.
(私の家は木で囲まれています。)
▶among the treeで『木に囲まれている』という意味です。
例文2 Among her class, she is very popular.
(彼女のクラスでは、彼女はとても人気があります。)
▶among her classで『彼女のクラスでは』という意味です。
③ between ➡ 特定のものに囲まれている
不特定のものに囲まれているaroundに対して、『特定のものに囲まれている状態』がbetweenのイメージです。
between London and New York(ロンドンとニューヨークの間)の物理的な隔たり以外に、between 9:00 and 11:00(9時から11時の間)のような時間や、between blue and white(青と白の間)のような程度なども表すことができます。
例文1 This train runs between Tokyo and Osaka.
(この電車は東京と大阪の間を走ります。)
▶between A and Bで『AとBの間』という意味になります。
例文2 His house is between the bakery and the bank.
(彼の家はパン屋と銀行の間にあります。)
④ during ➡ 特定の期間
特定の期間を表す場合に使います。
例文1 She can swim in the sea during the summer vacation.
(彼女は夏休みの間、海で泳ぐことができます。)
▶during the summer vacationで『夏休みの間』となります。
⑤ for ➡ 期間の長さ
期間の長さを表す場合に使います。
例文1 He is in London for five years.
(彼はロンドンに5年間います。)
▶for five yearsで『5年間』となります。
現在完了
現在完了は『過去と現在をつなぐ現在形』のことです。
過去の状況を『所有している』と解釈しているので、『助動詞have』を中心に文を作ることになります。
そして、過去との関連があるので『過去分詞(形容詞)』を使って表現しているのです。
たとえば、次の英文を見てみましょう。

『わたしは一度中国を訪れたことがある。』という文です、『have+Vpp』のカタマリがありますね。
これは下の図のように、過去と現在のつながりを表しているためです。

過去に中国を訪れたという『経験』を今も『所有している』というわけです。
また、現在完了では『have+Vpp』を動詞(V)としてみなしています。
深くは追及しませんが、have(助動詞)を中心にして文が成立していると考えてください。
なので、Can(助動詞)と同じように否定文や疑問文を作ることができるのです。

否定文はhave not(=haven't)とします。
それだけです。
これで『わたしは中国を訪れたことがありません。』となります。

疑問文はhaveを先頭に出すだけででき上ります。
答えるときは、もちろん『have』で答えてください。
現在完了は次のように文を作ることもできます。

副詞というのは名詞以外のことばを説明することばです。
副詞は説明する言葉の前に置くことが多いですので、このルールを覚えておいてください。
なので、今回もそのルールに従います。
『過去分詞washed』という形容詞の前に『just』という副詞があることに気づくと思います。
justはwashed(形容詞)を説明していますが、『ちょうど』という意味になります。
なので、この英文は『彼は皿をちょうど洗い終えたところです。』となり、『完了』を示していますね。
ん?終えるなんてどこにもないんじゃないの…?と疑問を持つ人がいると思います。

そもそも現在完了というのは、『過去と現在のつながり』を表しているという事を思い出してほしいのです。
ですので、過去に皿を洗っていて『ちょうど終えた!』といいたのです。
これは日本人の感覚に合わせるのではなく、英語圏の人の感覚に合わせないといけないという事ですね。
もう一つ現在完了の文を紹介したいと思います。

現在完了ではforは期間を表す前置詞になります。
ですので、この文を訳すと『わたしたちは5年間英語を勉強しています。』となるので『継続』を表すことになります。

ここで注意したいのは、『本当に5年間ずっと英語を勉強しているわけではない』という事です。
朝ごはんも食べずに、眠ることなく、遊ぶことなく、本当にずっと5年間英語を勉強していたのでしょうか?
ちがいますよね。
現在完了で表現できる『継続』というのは、あくまで断片的なものなのです。
じゃぁ、本当にずっとしているときはどう言えばいいの?
そんな疑問がありませんか?
そんなときに登場するのが『現在完了進行形』なのです。
次の英文を見てください。

現在完了『have been』と進行形『been reading』が合体していることが分かると思います。
現在完了は『have+Vpp』、進行形は『beV+Ving』ですので現在完了進行形は『have+been+Ving』となるのです。
これを訳すと『彼女は8時からずっと読書をしています。』となります。

簡単ですね!
ここで、わたしが中学生のときに現在完了の文で悩んだポイントを説明しておきたいと思います。
おそらく多くの人が悩んだと思います。
それは、forとsinceの違いです。
分かってしまえば簡単です。

forは期間、sinceは時期になります。
なので、上の文は『1時間』、下の文は『3時から』と訳します。
分詞
分詞ぶんしというのは『形容詞』のことです。
種類が二つありますが、どちらも形容詞のことです。
では、形容詞とはどのようなものでしょう?
少し身近な英文で考えてみましょう。

この場合、dogという名詞をcuteという形容詞が説明しています。
cuteのように形容詞のカタマリが1語の場合、前から説明します。

この場合は、to live inのように形容詞のカタマリが2語以上あるので、後ろから説明します。
これを後置修飾といいます。
これと同じことが分詞にも起こっているというだけの話です。
さて、分詞には2つの種類があります。

では、文章中では分詞をどのようにして見分けたらいいのでしょう?
分詞の見分け方について触れてみたいと思います。
Vingの見分け方とは?
そもそもVingは、次の方法で使われます。
・進行形
・動名詞
・現在分詞

Vppの見分け方とは?
Vppは、次の方法で使われます。
・受け身
・完了形
・過去分詞

では、実際に英文を作ってみましょう!

①は「あの眠っている男の子を見なさい。」となります。
sleepingはboy(名詞)を修飾しているので形容詞です。
つまり、現在分詞という事になります。

②は「これは壊された窓です。」となります。
brokenはbeVがあるので『受け身』かな…?と思いがちですが、『a』が挟まっていることに注意します。
brokenはwindow(名詞)を修飾しているので形容詞です。
つまり、過去分詞という事になります。
ここからは、後置修飾について説明をします。
後置修飾は文の構造が複雑になるので、次の手順で英文を訳していきます。
(1) 動詞(V)を見つける
(2) 分詞を見つける
では、次の英文を訳してください。
③ The boy playing soccer is Jiro.

正解は、『サッカーをしている少年は、次郎です。』
もう一問練習してみましょう。
次の英文を訳してください。
④ He has a car made in Japan.

正解は、『彼は日本でつくられた〔日本製〕車を持っています。』
分詞が難しいというより、形容詞の性質である後置修飾が難しいという事になりそうですね。
日本人にとって、後置修飾は複雑ですので落ち着いて処理をしていきましょう!
関係代名詞
まず最初に、関係代名詞というのは完全に論理単元だと思って下さい。
ですので、なんとなく感覚で解いている人がいるようですが、解法が完全に決まっているのです。
なので、英文の構造をしっかりと理解することが大切なのです。
Chapter1 説明編
関係代名詞というのは『形容詞』のことです。
厳密には違いますが、まずはこのように考えて下さい。
では、形容詞とはどのようなものでしょう?
例えば、少し身近な英文で考えてみましょう。

この場合、dogという名詞をcuteという形容詞が説明しています。
cuteのように説明する言葉が1語の場合、前から説明します。

分詞も形容詞なので、cuteと同様に扱うことができるのです。
形容詞(running)が1語なので、前から説明することができます。
では、2語以上で説明するときはどうなるのでしょう?

この場合は、running in the parkのように2語以上で説明する場合は、後ろから説明をします。
これを後置修飾といいます。

この場合も、written by Sousekiのように2語以上で説明しているので、後置修飾になります。
関係代名詞は、この後置修飾の事だと思って下さい。
少し関係代名詞の例文を見てみましょう。

この文の場合、who is wearing a hatがthe womanを説明しています。
whoって何?と思うかもしれませんが、who=the womanだと思って下さい。
whoは、the womanとそれ以降をつなぐ『のり』の役割をしていると思って下さい。
次の例文を見てみましょう。

この文の場合、which is taken by Tomがthe pictureを説明しています。
whichって何?と思うかもしれませんが、which=the pictureだと思って下さい。
whichは、the pictureとそれ以降をつなぐ『のり』の役割をしているのです。
ここで一つの疑問が生まれると思います。
どうして、さっきの文はwhoを使ったのに、今回はwhichを使ったの?というものです。
種明かしからすると、何を説明するかで使う『のり』が変わるのです。
人の説明をするときはwho、それ以外の説明をするときはwhichを使うのです。
また、関係代名詞には次のような性質があります。
その性質とは、主語と動詞があるということです。
関係代名詞は形容詞なのに主語と動詞があるの?という疑問があると思いますが、そこはとりあえず置いておきましょう。
今は、次の事だけを覚えて下さい。

さて、では実際に関係代名詞を含む英文に触れてみましょう。
次の英文を見て下さい。

※文型をまだ勉強していない人は、そちらを先に勉強しましょう。
この英文を見ると、ある事に気付くと思います。
それは、the boyと関係代名詞の主語(who)って同じものなんじゃないの?
ということです。
ご名答!その通りです。
who=the boyなのです。
つまり、この場合のwhoは関係代名詞の主語の役割を果たしているのです。
もう一つ例を見てみましょう。

この場合、which=a bookになります。
つまり、この場合のwhichは関係代名詞の主語の役割を果たします。
このように、関係代名詞の主語の役割を果たすものを『主格』と呼んでいます。
関係代名詞には主格以外にも使い方があるのでしょうか?
答えから言うと、『目的格』という使い方があります。
では、次は目的格について説明をしましょう。

さて、この英文を見て下さい。
whichは主格でしょうか?
違いますよね。なぜなら、whichの直後に『I』という主語があるからです。
では、このwhichは一体何者でしょう?
少し考えてみたいと思います。

関係代名詞の文を少し詳しく見てみましょう。
関係代名詞の文は『私は建てた』となっています。しかし、何を建てたのかという『目的語』がありません。
建てたのはもちろんthe houseですから、目的語=the houseになります。
この場合、目的語のthe houseをwhichに置きかえて『のり』の役割を果たしていたのです。
つまり、which=the house(目的語)だった訳です。
このように、関係代名詞が目的語の役割を果たすものを『目的格』といいます。
また、目的格には次の特徴があるので、覚えておきましょう。

Chapter2 練習編
次の英文を訳してください。
(1) The woman who is wearing a white hat is my sister.

和訳:白い帽子をかぶっている女性は私の姉です。
(2) The woman who is wearing a white hat talked to me yesterday.

和訳:白い帽子をかぶった女性は昨日私に話しかけた。
(3) The tree which stands by the road is very old.

和訳:道の側である木はとても古い。
(4) The picture which Ken took yesterday is beautiful.

解説:Ken took the picture(O) yesterday
⇨ the pictureがwhichになっています
和訳:ケンが昨日撮った写真は美しい。
(5) The boy that Ms. Green teaches English is my friend.

解説:teaches the boy English
⇨ the boyがthat(whom)になっています。
和訳:グリーンさんが英語を教えている少年は私の友達です。
(6) Mr. Kato will be transferred to the city which he grew up in.

解説:he grew up in the city.
⇨ the cityがwhichになっています。
和訳:加藤さんは生まれ育った街に引っ越すつもりです。
仮定法過去
仮定と結論からできている文には次の2つがあります。
①実際に実現する可能性があること
➁実際に実現する可能性がないこと(仮定法)
この2つの文の違いを理解することが非常に重要になります。
① 実際に実現する可能性がある仮定と結論
If you are hungry, I will cook lunch.
(もしお腹がすいているんなら、昼食をつくりますよ。)
仮定:If you are hungry
結論:I will cook lunch
この文の仮定は実際に実現する可能性がありますよね。
ですので、普通のIfの文になります。
If it's true, I will never see her again.
(もしそれが真実なら、二度と彼女には会わないよ。)
仮定:If it's true
結論:I will never see her again.
この文の仮定も実際に可能性がありますよね。
ですので、普通のIfの文になるのです。
If it smells bad, don't eat it.
(もし悪い臭いがしたら、食べないで!)
仮定:If it smells bad
結論:don't eat it.
この文の仮定も実際に可能性がありますよね。
ですので、普通のIfの文になるのです。
➁ 実際に実現する可能性がないこと(仮定法)
中学英語なので、仮定法過去について紹介します。
If I were you, I would ask someone to help.
(もし私があなたなら、誰かに手伝ってもらうように頼むでしょう。)
仮定:If I were you
結論:I would ask someone to help.
この文の仮定は、実際に起こる可能性がありませんね。
ですので、この場合は仮定法を使います。
仮定法のつくり方は、次のようになります。
(1) 『仮定』の時制を『結論』より一つ古くする
この場合、仮定は過去形、結論は現在形にしていますね。
(2) 結論に助動詞の過去を書く
(3) 仮定のbe動詞は、仮定法だと分かりやすくするためにwereを使う。
今回の場合、仮定の部分が過去形なので、『仮定法過去』と呼びます。
しかし、実際の時制は『結論』に合わせます。
ですので、現在形となります。
If I had some money, I would buy some cake.
(もし沢山お金があったら、ケーキを買うのに。)
仮定:If I had some money
結論:I would buy some cake.
仮定法過去の文です。
仮定の時制が結論よりも一つ古いことに着目してください。
そして、結論に助動詞の過去形を使っていますね。
I wish I could visit the zoo more often.
(もっと動物園に行っとけばよかった。)
仮定法には『結論』のみで完結する場合があります。
その場合、I wish(願望)の後に結論を書きます。
結論には助動詞の過去形を使いますね。
I wish I were a bird.
(鳥ならいいのに。)
仮定法には『仮定』のみで完結する場合があります。
その場合、I wish(願望)の後に仮定を書きます。
仮定には過去形を使いますね。
どうして助動詞の過去を使うの?
仮定法の結論にはどうして助動詞の過去を使うのでしょう?
その理由を説明するためには、助動詞の性質について説明をしなければなりません。
ここでは簡単に説明します。
助動詞は『主観的』な表現をするときに利用します。
主観的とは、自分中心の考え方の事です。
例えば、I can play the piano.の場合、『わたし』ができると思っているのです。
I am able to play the piano.の場合、『一般的に』にできるという表現になるのです。
つまり、そもそも助動詞には主観的なイメージがあるのです。
助動詞の過去形はそのイメージが飛躍して『気持ち』を持つことになります。
これは仮定法に限ったことではなく、次のような文でも応用できます。
Could you tell me the way to the station?
(駅への行き方を教えてもらえますか?)
どうして、過去でもないのに助動詞の過去を使っているのでしょう?
不思議に思った人はいるはずです。
なぜなら、助動詞の過去には『気持ち』がこもっているので、仮定法の意味合いが込められている事になるのです。
なので、この英文は『もしよければ、駅への行き方を教えてもらえませんか?』とダメ元で聞いているので、丁寧な言い方になるのです。
CouldやWouldは丁寧な言い方を表すと覚えている人がいると思いますが、それは当然の事だったのです。
どうして『仮定』の時制が『結論』より古いの?
実際に起こらない仮定のことを『反実仮想』といいます。
仮定が反実仮想なので、文法上もあり得ないものにして表現しようとしている訳です。
例えば、If I were a bird, I could fly to you.
(私が鳥なら、あなたのところへ飛んでいけるのに。)
仮定:If I were a bird
結論:I could fly to you.
この場合の仮定はあり得ないですよね!なので、文法もあり得ないwereを使っているのです。
そうすることで、この英文が仮定法だと分かりやすく工夫しているだけなのです。
なので、深い意味はありません。
・算数
割合
小学生の算数で、最難関になるのが割合の問題です。
苦手な人多いはずです。
割合が苦手で困っている子どもたちも多いのではないでしょうか?
そんな割合の文章問題を攻略する記事を作ってみました!
実際に問題を準備していますので、一緒に解きながら攻略していきましょう!
基本的な問題から、つまづきやすい重要な問題を準備しました!
これで、割合の問題には困りません。
割合の問題は中学生や高校生になっても数学として現れるので、勉強中の人は修得しておきたいですね('ω')ノ
割合の原理を理解しよう!
🔶分けるという考え方のことです!
割合とは、何かを分けるという考え方です。
たとえば、200個のみかんを10人に分けるとします。
すると、1人あたりは200÷10=20個になりますね。
これを1割と呼んでいるのです。
もし、200個のみかんを100人で分けたら、1人あたりは200÷100=2個になりますよね。
これを1%と呼んでいるのです。
ただそれだけのことです。
これが割合の根本的な考え方です。
ところで、割合には歩合と百分率があります。
歩合は、次のように決まっています。
10個に分けた1つ分(=0.1)を『1割』
100個に分けた1つ分(=0.01)を『1分』
1000個に分けた1つ分(=0.001)を『1厘』
百分率は、100個に分けた1つ分(=0.01)を『1%』と呼んでいます。
つまり、1分=1%、1割=10%となりますね。
では、次の問題を解いてみてください。
🌟問題1 700gの3割は何g?
🌟問題2 200$${m^2}$$の15%は何$${m^2}$$?
🌟問題3 3000$${mL}$$の2割3分は何$${mL}$$?
答えは下にあります。
解答
🌟問題1 210g
3割なので、10個に分けた3つ分として考えます。
なので、700÷10×3=210
🌟問題2 30$${m^2}$$
15%なので、100個に分けた15つ分として考えます。
なので、200÷100×15=30
🌟問題3 690$${mL}$$
2割3分=23%なので、100個に分けた23つ分として考えます。
なので、3000÷100×23=690
割合の性質を理解しよう!
🔶~は→=、~の→×で表せる
簡単な例で実験してみましょう。
6の9倍は54です。
これを数式で表すと、6×9=54になります。
この関係を日本語と数式で照らし合わせてみます。

『の』が×、『は』が=になっていますね。
この性質を利用して問題を解きます。
では、54は6の何倍でしょう?
この場合、次のようになります。

なので、◇=54÷6=9になるので、9倍となります。
表現が変わっても、『~の、~は』に書き換えて問題を解きます。
では、次の問題を解いてみてください。
🌟問題1 48歳は12歳の何倍?
🌟問題2 10Lを何倍すると48Lになる?
🌟問題3 兄の体重は48㎏、妹の体重は20㎏です。兄の体重は妹の体重の何倍?
答えは下にあります。
解答
🌟問題1 4倍
48=12×◇より、◇=48÷12=4
🌟問題2 4.8倍
「10Lの◇倍は48L」と書き変えます。
すると、10×◇=48となるので、◇=48÷10=4.8
🌟問題3 2.4倍
「48㎏は20㎏の何倍」と書き変えます。
すると、48=20×◇となるので、◇=48÷20=2.4
割引き、割増しの問題は簡単!
🔶割合は全体を1として考えています
そもそも割合というのは全体を1として考えています。
ですので、1=10割=100%となるのです。
では、3割引きの場合、全体の何割のことを表しているのでしょう?
3割引きというのは、全体の10割から3割を引くという意味なので、7割のことを表します。
また、3割増しというのは、全体の10割に3割を加えるという意味なので、13割のことを表します。
では、2000円の3割引きはいくらになるでしょう?
3割引きとは10-3=7割のことですので、2000÷10×7=1400円となります。
2000円の3割増しの場合はどうなるでしょう?
3割増しとは10+3=13割のことですので、2000÷10×13=2600円になるのです。
では、次の問題を解いてみてください。
🌟問題1 1200mLの2割増しは何mL?
🌟問題2 4800円の6割引きはいくら?
🌟問題3 280円の税込価格を求めましょう。※消費税10%
答えは下にあります。
解答
🌟問題1 1440mL
2割増しは12割のことなので、1200÷10×12=1440円
🌟問題2 1920円
6割引きは4割のことなので、4800÷10×4=1920円
🌟問題3 308円
10%増しのことなので、110%になります。
280÷100×110=308円
食塩水の問題は割合で攻略する!
🔶食塩水は水に食塩を加えたもの
ここに3%の食塩水が500gあります。
この食塩水には何gの食塩と水が含まれているでしょう?
まず、3%の食塩水というのは、食塩水の3%が食塩という意味です。
つまり、食塩の量は500÷100×3=15gとなります。
なので、水の量は500-15=485gとなるのです。
では、次にこの食塩水に水を加えて2%にします。
水を何g加えたらよいか考えてみます。
食塩の量は全体の2%で15gあります。
つまり、水の量は全体の98%ということになります。
全体の1%は15÷2=7.5gなので、98%は7.5×98=735gです。
なので、水が735gあればいいことになります。
いま水は485gあるので、735-485=250g加えたらいいことになりますね。
次は2種類の食塩水を混ぜてみます。
2%の食塩水500gと5%の食塩水100gを混ぜると何%の食塩水になる?
2%の食塩水には500÷100×2=10g、5%の食塩水には100÷100×5=5gの食塩が含まれています。
つまり、食塩水は600g、食塩は15gあることになります。
ここで、「食塩15gは食塩水600gの何倍か」と書き変えます。
すると、15=600×◇となり、◇=15÷600=0.025=2.5%になります。
では、次の問題を解いてみてください。
🌟問題1 4%の食塩水300gには何gの水が含まれているか?
🌟問題2 5%の食塩水100gに何gの水を加えると4%の食塩水になるか?
🌟問題3 6%の食塩水300gと8%の食塩水200gを加えると何%の食塩水になるか?
答えは下にあります。
解答
🌟問題1 288g
食塩の量は300÷100×4=12gになるので、水の量は300-12=288g。
🌟問題2 25g
5%の食塩水に含まれている食塩は100÷100×5=5g、水は100-5=95gです。
4%の食塩水にも5gの食塩が含まれていることから、全体の1%の量は5÷4=1.25gと分かります。
水の量は全体の96%あるので、1.25×96=120gの水があればいいことになります。
水は95gあるので、120-95=25g加えたらいいのです。
🌟問題3 6.8%
6%の食塩水300gには300÷100×6=18g、8%の食塩水200gには200÷100×8=16gの食塩が含まれています。
2種類の食塩水を混ぜると、食塩水は500g、食塩は34g含まれていることになります。
ここで、「食塩34gは食塩水500gの何倍か」と書き変えます。
すると、34=500×◇となり、◇=34÷500=0.068=6.8%になります。
算数・数学の素朴な疑問5選
みなさんは、算数・数学の素朴な疑問はありませんか?
「偉い人が決めたことだから、考える必要ないんじゃないの?」と感じていることってあるのではないでしょうか?
わたしが子どものころに感じた素朴な疑問は次の5つです。
① 分数のわり算ってどうして逆算にしてかけるの?
➁ どうして0で割ったらいけないの?
③ マイナス×マイナスってどうしてプラスなの?
④ 小数と分数のパラドックス
⑤ 円周率の謎?
至極当然のように使われている事ですので、大学生でも答えられない人が多いようです。
そんな疑問を解決してみたいと思います。
pattern1 分数のわり算ってどうして逆数にしてかけるの?
分数のわり算は逆数にしてかけ算にしなさい!
なぞの呪文を小学校のときに教えられた人は多いと思います。
ここでは、その謎を解明してみたいと思います。
まず、次の計算を見て下さい。
$${13÷13=1}$$
この計算のように、割る数と割られる数が同じ場合、答えは1になります。
$${0.13÷0.13=1}$$
これもひっ算をすれば、答えは1になります。
このことから、割られる数と割る数が同じ場合、答えは1になることが分かります。
ですので、一般的に$${a}$$を実数とすると、$${a÷a=1}$$となることが分かります。
さて、次の分数のわり算を考えてみましょう。
$${\dfrac{2}{3}÷\dfrac{5}{7}}$$
分数のわり算は、この式に『1』をかけることで解決します。
1をかけても、答えは何も変わらないよね…。
そう感じると思いますが、実は何も変わらないというのが重要なのです。
では、解いてみます。
$${\dfrac{2}{3}÷\dfrac{5}{7}×1}$$
※1をかけます。
$${=\dfrac{2}{3}÷\dfrac{5}{7}×\dfrac{5}{7}×\dfrac{7}{5}}$$
※1を割る数に合わせて分解します。
$${=\dfrac{2}{3}×\dfrac{7}{5}×\dfrac{5}{7}÷\dfrac{5}{7}}$$
※かけ算わり算の式は、順番を並べかえることができます。
$${=\dfrac{2}{3}×\dfrac{7}{5}×1}$$
※後半の後ろ2つは1になりますね。
$${=\dfrac{2}{3}×\dfrac{7}{5}}$$
※結論として、逆数をかけ算にしてかけることになりそうです。
この性質を『決まり』として暗記させられていたという訳ですね。
Pattern2 どうして0で割ったらいけないの?
0を割ってもいいけど、0で割ったらいけない?
理由は『決まりだから!』そう習っている人が多いようです。
ここでは、その謎について解明したいと思います。
ここでは、理屈ではなく論理で片づけます。
まず最初に、わり算の性質を説明しておきます。
$${27÷9=3}$$の場合、$${9×3=27}$$となりますね。
この性質をよく覚えておいてください。
まずは、0を割るパターンから説明します。
$${0÷7=x}$$とします。
すると、$${7×x=0}$$となり、$${x=0}$$となります。
ですので、$${a,x}$$を実数とする$${(a≠0)}$$と、次の性質があることになります。
$${0÷a=x}$$
$${a×x=0}$$なので、$${x=0}$$
※0を割ると、答えは0に決まるという事になります。
次に、0で割るパターンを説明します。
$${7÷0=x}$$とします。
すると、$${0×x=7}$$となり$${x}$$は存在しません。
※$${x}$$に何を当てはめても成り立つことがないという意味です。
ですので、$${a}$$を実数とすると、次の性質があることになります。
$${a÷0}$$の答えはない。
※0で割ると、答えが出ないので割ってはいけないという訳です。
さいごに、0を0で割ってみます。
$${0÷0=x}$$とします。
すると、$${0×x=0}$$となり、$${x}$$はどんな数でもいい事になってしまいます。
0で割ると、答えが出ないか、どんな数でもいい事になってしまうので、算数や数学ではタブーになっているのです。
Pattern3 マイナス×マイナスはどうしてプラスなの?
マイナス×マイナスはプラスになります!
反対の反対はもとに戻るからです!と、謎の呪文を中学生のときに教えられた人は少なくないはずです。
どうして、マイナス×マイナスはプラスのなるのでしょう。
その理由を説明したいと思います。
まずは、$${2×0=0}$$。
これは正しいですよね。
では、$${3-3=0}$$。
これも正しいですよね。
なので、$${2×(3-3)=0}$$。
これも正しい事になります。
分配法則を利用すると、$${2×3+2×(-3)=0}$$となります。
なので、$${2×(-3)=-6}$$となります。
ここから、プラス×マイナスはマイナスになることが分かります。
次に、$${-2×0=0}$$とします。
すると、さっきと同様に$${-2×(3-3)=0}$$となります。
分配法則を利用すると、$${-2×3-2×(-3)=0}$$となります。
なので、$${-2×(-3)=6}$$となります。
ここから、マイナス×マイナス=プラスになることが分かりますね。
あとは、時間がある人は文字で説明をしてみて下さい。
Pattern4 小数と分数のパラドックス
1=0.9999999999…であることを説明してみたいと思います。
こんなの絶対に成り立たない!そう感じるかもしれませんが、実は成り立ってしまうのです。
$${x=1,y=0.9999…}$$とします。
すると、$${x+y=1.9999…}$$となります。
ここで両辺を2で割ると、$${\dfrac{x+y}{2}=0.9999…}$$
$${y=0.9999…}$$より、$${\dfrac{x+y}{2}=y}$$
両辺2倍すると、$${x+y=2y}$$より$${x=y}$$。
つまり、1=0.99999999999…という事になりますね。
逆をいうと、これを認めた上で計算をしているという事になるのです。
Pattern5 円周率の謎?
円周率というのは、円周を円の直径で割ったものです。
つまり、言いかえると円の直径に円周率をかけると円周になるのです。
円周って『ここからここまで!』って、決まっていますよね。
なのに、円周率が無理数って意味不明だと思いませんか?
無理数というのは、小数点以下が限りなく続く数のことです。
この疑問の答えは、円の直径から求められる円周の長さは、およその数だというものです。
ですので、正確な長さを求めることはできません。
円周率を『π』という文字を使っているのは、正確な値を求めることができないから誤魔化しているのです。
正確に求められないんだったら、正確な値を文字にしちゃえばいいんじゃない?というノリでしょうか。
・数学の関する記事
・素因数分解
・オイラー関数
・規則性
・立方体の個数
・数学の素朴な疑問5選
・連立方程式の文章問題
・積分の攻略[超基礎編]
・積分の攻略[特殊編]
・積分の攻略[部分積分編]
・積分の攻略[分数関数編]
・積分の攻略[三角関数のみで表される編]
・積分の攻略[高次の三角関数の積分編]
・積分の攻略[積分方程式編]
・ユークリッドの互除法
・数学の能力は社会で生きるのか?
・中学理科
・クイズ
論理クイズ1 1kgの鉄と1kgの綿
1kgの鉄と1kgの綿を高い場所から同時に落とすと、先に地面に落下するのはどちらでしょう?
論理クイズ2 お酒って何歳から買えるの?
お母さんから買い物を頼まれた7歳の太郎君。
コンビニでお酒を買うように頼まれたのですが、店員に止められることなく、普通にお酒を買えてしまいました。
お母さんが太郎君に『きちんと買えた?』と質問をすると、返事をしっかりしたそうです。
どうして、太郎君は成人していないと買えないはずのお酒を買う事ができたのでしょう?
論理クイズ3 正直村と嘘つき村
ある旅人が、正直村を目指して旅をしていると、二つの分かれ道に到着しました。一方は正直村、もう一方は嘘つき村に続いているのですが、どちらが正しい道か分かりません。
困り果てていると、一人の男性に出会いました。この男性は正直村から来たのか、嘘つき村から来たのかが分からないのですが、ある質問をすることで、正直村の方向が分かったそうです。
正直村の人は正しい事だけ、嘘つき村の人は誤った事しか話しません。
さて、どのような質問をすれば、確実に正直村へ辿りつけるのでしょう?
論理クイズ4 井戸からの脱出
深さ30mある古びた水のない井戸に女の子が落ちてしまいました。その女の子は、1分間に3mのぼることができますが、すぐに2m下がってしまいます。さて、この女の子が井戸から脱出できるのは何分後でしょう?
論理クイズ5 消えた1ドル
あるサラリーマン3人が1泊10ドルのホテルに泊まることにしました。合計で30ドルです。しかし、3人で宿泊した場合25ドルとなるキャンペーンがあったことに気づいた受付係は、5ドルを返金しようとしました。
しかし、3人で5ドルだともめる可能性があったため、残りの2ドルは受付係が自分のポケットに入れてしまいました。
さて、サラリーマン3人はそれぞれ9ドルずつホテル代を支払っているので、9ドル×3人=27ドル。それと受付係がくすねた2ドルと合わせると合計で29ドルになります。あと1ドルはどこに消えてしまったのでしょう…?
論理クイズ6 少なすぎる情報
ある泥棒に宝石が盗まれてしまいました。容疑者はA、B、Cの3名です。
容疑者Aは『犯人はBだ!』と主張しているのですが…。
さて、犯人はA、B、Cのいづれか一人です。犯人だけが正しい事を言うようなのですが、一体だれが犯人なのでしょう…?
論理クイズ7 3つの電球
あなたはある部屋Aにいます。ある部屋Aには➀➁③の3つのスイッチがあり、隣の部屋Bの3つの電球とつながっています。部屋Aから部屋Bの電球を見ることができず、一度部屋Aを出ると部屋Bには行けますが、部屋Aに戻ることはできないようです。
さて、部屋Aのスイッチと部屋Bの電球がどのようにつながっているかを調べるにはどのようにすればよいのでしょう?
論理クイズ8 ウイルスの増殖
ビンの中にウイルスが1匹います。このウイルスは1分で2倍に増殖する性質を持っているのですが、120分でビンの中がウイルスでいっぱいになってしまうそうです。ビンの容量の25%分だけウイルスが欲しいとき、何分後に増殖をやめさせればいいでしょうか?
論理クイズ9 3枚のトースト
3枚の食パンがあります。この食パンの裏表を焼きたいのですが、片面を焼くのに30秒かかります。使うことができるのは一度に2枚のトーストを焼けるフライパン1枚だけです。
3枚のトーストの裏表を焼き上げるには最短で何秒かかるでしょう?
論理クイズ10 箱の中の白いボール
中が見えない箱の中に、白か黒のボールが1つだけ入っています。この箱の中に白いボールを1つ追加して、よく混ぜた後、ボールを1つ取り出したところ白玉だったそうです。
では、箱の中に白玉が残っている確率は?
論理クイズ11 変なレース
ある旅人2人が馬に乗ってレースをすることになりました。それぞれ自分の馬に乗ってレースをするのですが、このレース、遅くゴールした者が勝ちだというのです。このレースの主催者は、勝った馬の主に賞金を与えたいそうなのですが、なかなか勝負が決まりません。何か良い知恵はないでしょうか?
論理クイズ12 空き缶のリサイクル
ジュースの空き缶を5本持ってくると、新しいジュースが1本もらえるそうです。今、このジュースをあなたは200本持っているのですが、最大で何本のジュースを飲むことができるのでしょう?
論理クイズ13 500枚のコイン
今、同じ種類のコインが500枚あります。表面を向ているコインが10枚、あとの490枚は裏面を向いています。目隠しをして、この500枚のコインを2つのグループに分けて、それぞれのグループにある表面のコインの数を同じにしたいのですが、どうすればいいのでしょう?
論理クイズ14 ジャンケンの勝利者
2人の中年男子、太郎と次郎がジャンケンをしました。
太郎は、グーを3回、チョキを6回、パーを1回、
次郎は、グーを2回、チョキを4回、パーを4回出しました。
出した順番は分かりませんが、あいこは一度もなかったということは分かっています。さて、多く勝ったのはどちらでしょう?
論理クイズ15 宝石を無事に届ける方法
太郎君は花子さんに宝石を送りたいと思っています。しかし、花子さんが住んでいる地域は治安が悪く、宝石をそのまま送ると盗まれてしまうので、箱に南京錠をかけてその中に宝石を入れて送ることにしました。
南京錠に鍵をつけて送ると、当然中身の宝石は盗まれてしまいますし、鍵だけを送っても鍵は盗まれてしまいます。箱ごと盗まれることはないようです。
南京錠はどこでも手入れることができるそうなのですが、どのように工夫すれば、太郎君は花子さんに無事宝石を届けることができるのでしょう?
論理クイズ16 天使と悪魔と人間
天使、悪魔、人間の3人がいます。
天使はいつも正しい事をいい、悪魔はいつも間違ったことをいいます。そして、人間は正しい事と間違ったことを交互に言います。ただし、どちらが先なのかはわかりません。
今、目隠しをしたあなたは『赤いカード』と『青いカード』がたくさん入った箱を持っています。その中から1枚取り出して聞いたところ、Aは『青』、Bは『青』、Cは『赤』と答えました。
さらに、もう1枚取り出して聞いたところ、Aは『赤』、Bは『青』、Cは『青』と答えたそうです。声はみんな同じだとします。
さて、A、B、Cのうち人間はどれなのでしょう?
論理クイズ17 2種類の錠剤
病気になってしまったあなたは、全く同一の2種類の錠剤AとBを毎日1粒ずつ飲まなければならなくなってしまいました。
ある日、Aの錠剤1粒とBの錠剤を2粒混ぜてしまい、全く見分けがつかなくなってしまいました。毎日1粒ずつ飲まなければならないのですが、何か良い知恵はないでしょうか?なお、この薬は高価なため諦めたくありません。
論理クイズ18 3枚のカード
3枚のカードがあります。
1枚は両面が黒、1枚は両面が白、1枚は表面が白、裏面が黒です。
箱の中に3枚のカードを入れて、無作為に取り出しました。
そうすると、そのカードの表面は白だったそうです。
では、そのカードの裏面が白である確率は?
論理クイズ19 17匹の猫
17匹の猫がいます。
A、B、Cの3人でこの猫を引き取ることになったのですが、次の条件があるようです。
・Aは全体の2分の1を引き取る
・Bは全体の3分の1を引き取る
・Cは全体の9分の1を引き取る。
このままでは上手く分けることができないのですが、偶然通りかかった友人がよい知恵をくれたそうです。
この友人はどんな知恵を与えてくれたのでしょう?
論理クイズ20 給料の支給方法
会社から給与の提案をされました。あなたならどちらのプランを選びますか?
・プランA 1年に1回10万円昇級、1年に1回1年分を支給。
・プランB 半年に1回3万円昇級、半年に1回半年分を支給。
論理クイズ21 7つのLEDライト
7つのLEDライトがあります。何色かに光るそうなのですが、同じ色に光るライトは4つ以上あるようです。
このLEDライトは同じ色に光るもの同士をくっつけるとその色に光るのですが、違う色の場合は何も変化がありません。
このLEDライトを同時にくっつけることができるのは2つまでで、暗闇の中で作業するので、LEDライトが光るまで色が分かりません。
最も多い色のLEDライトを1つ持ち帰りたいのですが、最短で何回の作業で確かめることができるのでしょう?
論理クイズ22 4枚のカード
$${\fbox{K}, \fbox{A}, \fbox{6}, \fbox{1}}$$の4枚のカードがあります。
このカードの裏面には、アルファベットの裏には数字が、数字の裏にはアルファベットが書かれています。
いま、2枚だけ裏返して、『母音が書かれたカードの裏には偶数が書かれている』というルールを確かめたいのですが、どの2枚のカードを裏返せばいいのでしょう。
論理クイズ23 コーヒーとミルク
A、B2つのカップがあります。
Aにはミルクが、Bにはコーヒーが入ってます。
いま、Aからミルクをスプーンで1杯だけBに移します。そして、よくかき混ぜてから、さっきと同じ量をAに戻します。
このとき、Aの中にあるコーヒーの量は、Bの中にあるミルクの量より多いのでしょうか?
論理クイズ24 飛行機の飛行時間
空港A、Bがあります。
いま空港Aを出発して空港AB間を往復します。
AB間が無風のときと、空港Aから空港Bへ常に風が吹いているときとでは、どちらが時間がかかるでしょう?
※飛行機のエンジン回転数や風速は常に一定とします。
同じっぽいですが…。
論理クイズ25 鍵を解除して牢獄から突破せよ!
A、B、Cの三人が、それぞれ別の場所の牢獄に監禁されてしまいました。
牢獄から脱出するにはダイヤル式の鍵を解除しなければなりませんが、
鍵は000~999の三ケタで、3人とも同じ番号だそうです。
左から1ケタ目をA、2ケタ目をB、3ケタ目をCが特別に教えられているそうです。
この鍵のダイヤル数をすべてたすと9になり、右のケタの数は左のケタの数以上だそうなのです。
3人はお互いに通信をとることができませんが、牢獄から誰が出たかはすぐに分かるようになっているそうです。
しばらく、3人は牢獄から出ることができなかったのですが、その様子を見たBはすんなりと牢獄から出ることができたそうです。
さて、3ケタのダイヤル番号は何だったのでしょう…?
論理クイズ26 運動会の順位
A、B、Cの3人だけで運動会をすることになりました。
各競技では1位、2位、3位にそれぞれ$${x}$$点、$${y}$$点、$${z}$$点が与えられます。
ただし、$${x>y>z>0}$$の整数とします。
全競技が終わったところ、Aは全体で22点。
Bは槍投げで1位になり、全体で9点。
Cは全体で9点という結果になりました。
さて、100m走で2位になったのは誰でしょう?
100m走なんて出てきてないじゃん…。とツッコミを入れたくなりそうな問題ですが…。
論理クイズ27 好きな人の誕生日はいつ?
トムとジェリーは、とらねこと友だちになったばかりです。
そんなトムとジェリーは、とらねこの誕生日を知りたいということだったので、とらねこのは次のヒントを出すことにしました。
誕生日は次の中にあります。
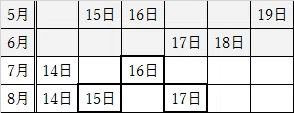
5月15日、5月16日、5月19日、6月17日、6月18日、7月14日、7月16日
8月14日、8月15日、8月17日
これだけでは分からないので、とらねこはトムには誕生月を、ジェリーには日付だけを教えることにしました。
そうすると、トムは『ジェリーも分からない!』と断言しましたが、その後、ジェリーはトムの言葉を聞いて分かったそうなのです。
そして、しばらくしてトムも分かったそうなのですが、とらねこの誕生日は一体いつなのでしょう?
論理クイズ28 監視し合う囚人
囚人が沢山います。
その囚人たちに自分から最も近い囚人を監視するように言いつけます。
囚人と囚人の距離で同じものはなく、囚人の人数は奇数だということが分かっています。
さて、この状況で誰からも監視されない囚人はいるのでしょうか?
論理的に説明してほしいとのことです。
論理クイズ29 数当てクイズ
とらねこと数当てクイズでもしましょう。
とらねこは、1~100までの数の中で1つだけ持っています。
ヒントを出すので当ててみて下さい。
・その数は2で割り…。
・その数は3で割り…。
・その数は5で割り…。
・その数は7で割り…。
「よく聞こえなかったようですね…。よく聞いていればわたしの持っている数が分かるのですが…。」
おや、この質問のうち、1つだけ聞き取れた人があなたの側にいるようで、その数で割り切れるそうです。そして、その人はわたしの数が分かったそうですね。
さて、わたしの持っている数は何でしょう?
解答・解説
1.真空状態の場合は同じ。でも、そうでない場合は『分からない』が正解です。
同じ1kg でも体積や形は異なります。体積が異なると表面積は変わるのですが、綿をすごく凝縮してフェルトのようにして固めたとします。鉄を薄く延ばして紙のようにしたとします。そうすると、綿は地面にすぐに落ちますが、鉄はひらひらと舞ってしまいなかなか地面に落ちることはないのです。
1kgと表現されると、球の状態をイメージする人が多いという先入観を利用した問題でした。
2.太郎君は犬だったから。
20歳未満はお酒を買う事ができないというのは、人間に限ったことです。
太郎君は近所でも有名な優秀な盲導犬なのです。お母さんは目と耳が不自由なので、一緒におつかいに行っていたのです。
お母さんの質問に対して、太郎君は『ワン!』という返事をしたそうです。
3.あなたが来た村の方向を指さしてください。
出会った男性がどちらの村の人間であっても同じ答えを出してもらわなければなりません。
そのためには、『出身村』を答えてもらえばいいのです。
もし、正直村の人であれば、正直に自分の村の方を指します。
もし、嘘つき村の人間であれば、嘘をつかなければならないので、正直村の方を指さすしかないのです。
つまり、どちらの村の人でも、正直村を指さすという訳です。
4.残念ながらこの女の子が井戸から出てくることはありません。
深さ30mといえば、ビルの10階相当になります。そんなところに落ちてしまったら無事では済まないでしょう。つまり、その女の子が自力で出てくることはないということです。
もし仮に、この問題文通りにのぼっていくと、28分後に出ることができますが、現実的にはかなり厳しいと思います。
5.1ドルはどこにも消えていない。
$${\fbox{解説}}$$
$${\begin{array}{|c|c|c|}\hline&サラリーマン&ホテル側 \\ \hline最初&30ドル&30ドル\\ \hline返金後&27ドル&25ドル\\ \hline横領2ドル&25ドル&25ドル \\ \hline\end{array}}$$
サラリーマンとホテル側のバランスシートを見ると分かりやすいかもしれませんね。ホテル側は最終的に25ドル受け取っていることになります。サラリーマンは確かに27ドル支払っていますが、2ドルは受付人が横領していますので、サラリーマン側が2ドル受け取っているとみなさなければならないのです。ですので、このやり取りでおかしいところは何もなかったという事です。
6.容疑者C
少なすぎる情報をどのように捉えるかがポイントになります。
仮にAが犯人だと仮定します。そうすると、Bが犯人だという事になってしまうので、犯人が二人となってしまい矛盾します。つまり、Aは犯人ではありませんので、本当のことをいいません。よって、Bも犯人ではないという事です。なので、犯人はCだという事になります。
実際はこのような方法で犯人を断定することはできませんが、論理クイズという事で…。
7.➀のスイッチを10分つけて消します。そして、➁のスイッチをつけてBの部屋へ移ります。
電球はしばらくつけておくと、ほんのり温かくなります。その性質を利用します。➀のスイッチを10分つけていると、Bの部屋の➀とつながっている電球は温かくなります。➁のスイッチをつけると、Bの部屋の➁とながっている電球はついています。Bの部屋の触っていも冷たい電球が、③のスイッチとつながっている電球だという訳です。
8.118分後。
120分でウイルスがビンいっぱいになってしまうという事は、その1分前はビンの50%がウイルスで満たされていたという事です。そして、さらにその1分前はビンの25%がウイルスで満たされていたことが分かります。
つまり、120-2=118分後ということが分かります。
9.90秒。
3枚の食パンをA、B、Cと名前をつけておきます。そして、それぞれの食パンの表面を○、裏面を×とでもしておきましょう。そうすると、下の表のようにまとめることができます。
$${\begin{array}{|c|c|c|c|}\hline&A&B&C\\ \hline30秒&○&○\\ \hline60秒&×&&○\\ \hline90秒&&×&×\\ \hline\end{array}}$$
これが最短になるので、正解は90秒となります。
10.$${\cfrac{2}{3}}$$
確率というのは、可能性のことをいいます。ですので、可能性をすべて書き出してみたいと思います。
1)最初に黒玉が入っていた場合
取り出すことができるのは白玉か黒玉の2通り
2)最初に白玉が入っていた場合
取り出すことができるのは白玉か白玉の2通り
つまり、全部で4通りの取り出し方があるわけですが、白玉は1つ取り出しているのですから、箱の中は(白玉、白玉、黒玉)の可能性があることになります。よって、箱の中に白玉が残っている確率は$${\cfrac{2}{3}}$$となりますね。
11.旅人の馬を乗り換えればいいい。
レースの主催者が、「馬の持ち主に賞金を与える」といっているので、相手の馬に乗り換えて、はやくゴールすればいい事になります。
12.249本。
最初に200本ジュースがあるので、これをまず全部飲んだとします。…200本
そうすると、空き缶が200本できるので、これをジュースに変えると、200÷5=40本のジュースと交換してもらえます。
そして、この40本のジュースをすべて飲んだとします。…240本
そうすると、さらに空き缶が40本できるので、これをジュースに変えると、40÷5=8本のジュースと交換してもらえます。
そして、この8本のジュースをすべて飲んだとします。…248本
そうすると、さらに空き缶が8本できるので、これをジュースに変えると、8÷5=1本…3(空き缶)となり、1本のジュースと交換してもらえます。
そして、この1本のジュースを飲みます。…249本
これ以上は、ジュースと交換することができないですね。
13.10枚と490枚のグループに分けて、10枚のグループのコインを全て裏返す。
10枚のグループには、$${x}$$枚の表コインと$${10-x}$$枚の裏コインがあります。一方、490枚のグループには$${10-x}$$枚の表面のコインがあることになるので、10枚のグループのコインを全て裏返すと、同じになるという訳です。
例えば、10枚のグループに表コインが2枚あるとします。すると、490枚のグループには表コインが8枚あります。そこで、10枚のグループのコインを全て裏返すと、裏コイン8枚が表コイン8枚に変わりますね。
14.太郎。
太郎君のチョキの回数が一番多いので、これを基準にします。
そうすると、あいこはないので、太郎君が6回チョキを出したとき、次郎君は2回グーを、4回パーを出していることになります。この時点で太郎君は4回勝っていることになります。
次に、次郎君が4回チョキを出した事を考えると、太郎君は3回グーを、パーを1回出すことになるので、さらに太郎君が3回勝つことになります。
つまり、この勝負、太郎君が7回、次郎君は3回勝っているので、多く勝ったのは太郎君となるのです。
15.太郎君は箱の中に宝石を入れて南京錠Aをつけて鍵をして、花子さんに送ります。
受け取った花子さんは、宝石の入った箱に南京錠Bをつけて鍵をして、太郎君に送り返します。…この時点で、箱には南京錠A、Bの2つがあります。
受け取った太郎君は、南京錠Aの鍵を外して花子さんに送り返します。
受け取った花子さんは、南京錠Bを鍵を使って開けて、箱の中の宝石を受けとります。
『南京錠はどこでも手入れることができる』というヒントから、花子さんも南京錠を使えるという事に気づけるかがポイントだったと思います。太郎君が送るので、南京錠を使えるのが太郎君だけという先入観があった人は多いのかもしれませんね。
また、箱に南京錠を2つつけるという発想も大切だったと思います。通常、南京錠って1つしかつけることがないので、この発想の転換は難しかったのかもしれませんね。
16.B。
天使は正しい事を悪魔は嘘を言うので、天使と悪魔が答える色は違う事になります。つまり、A、Cのいずれかが天使、悪魔だということが分かります。つまり、人間はBです。
もし、Aが天使なら、人間は『正しい事→嘘の事』の順で答えたことになり、もし、Cが天使なら、人間は『嘘の事→正しい事』の順で答えたことになります。A、Cの特定はできませんが、Bが人間だという事だけは確定するのです。
17.Aをもう一錠準備します。そして、4錠を半分にして1日目に半分、2日目にもう半分を飲めば解決できる。

Aを1粒加えて2つに分けることで、図のようになります。1日目に左半分、2日目に右半分を飲めば、量を間違えることがありません。
18.$${\dfrac{2}{3}}$$。
白(表)ー白(裏)
白(裏)ー白(表)
白(表)ー黒(裏)
取り出した面が白である場合は、上の3通りです。
そして、裏面も白色であるのは2通りです。
ですので、確率は$${\dfrac{2}{3}}$$となります。
取り出したときに白色だったので、白色の裏面の事を考えればいいという問題だったわけです。
19.1匹猫を連れてきて、18匹にして分ける。
分けた後、自分が連れてきた猫を連れてかえる。

少し難しいので画像を作成しました。
友人が猫を1匹連れてくると、合計で18匹になります。
そうすると、Aさんは9匹、Bさんは6匹、Cさんは2匹で条件を満たすことになります。そして、自分が連れてきた猫を引き取ればいいというわけです。
この問題のポイントは、17匹の猫を分けるとは書いていないということです。『全体』という表現をどのように捉えるかがカギになったのではないでしょうか?
20.プランBの方が得。
$${\begin{array}{|c|c|c|c|c|c|c||c|}\hline&6カ月&12カ月&18カ月&24カ月&30カ月&36カ月&合計\\ \hlineプランA&0&0&0&10&0&20&30\\ \hlineプランB &0&3&6&9&12&15&35\\ \hline\end{array}}$$
実際に表をかいて確かめてみると、プランBの方が得だということが分かります。
初回の給料受取日には昇級はないですね、ですので、次回から昇級は適用されることになります。
冷静に観察すると、プランBの方が1年目から得になるのです。
21.7つのLEDライトを$${\fbox{A}}$$,$${\fbox{B}}$$,$${\fbox{C}}$$,$${\fbox{D}}$$,$${\fbox{E}}$$,$${\fbox{F}}$$,$${\fbox{G}}$$とします。
ここで、
$${\fbox{A}\fbox{B}}$$,$${\fbox{C}\fbox{D}}$$,$${\fbox{E}\fbox{F}}$$の確認をすれば、どれが一番多いLEDライトなのかを1つだけ特定することができます。
難しいパターンで検証してみましょう。
検証1>

この場合、$${\fbox{G}}$$を取れば確実という事になります。
同じ色のLEDライトは4つ以上あるので、$${\fbox{A}\fbox{B}}$$,$${\fbox{C}\fbox{D}}$$,$${\fbox{E}\fbox{F}}$$それぞれのグループの中に同色が1つないといけないことになります。
つまり、$${\fbox{G}}$$は4つ目だという訳です。
何色かは分かりませんが、一番多い色のLEDライトを選んだのは確かです。
検証2>

この場合は、やはり$${\fbox{G}}$$をどう受け止めるかがポイントになります。
同色が4つないといけませんので、$${\fbox{G}}$$が何色か分からなくても、これをとることになります。
$${\fbox{E}\fbox{F}}$$の中に3つ目があり、$${\fbox{G}}$$は4つ目になるからです。
ですので、$${\fbox{G}}$$は何色かはわかりませんが、一番多いい色を取ったことになるのです。
▶検証3>

この場合は、$${\fbox{A}\fbox{B}}$$で黄色に点灯しているので、分かりやすいと思います。もし、赤や青でそろえようと思ったら、$${\fbox{C}\fbox{D}}$$と$${\fbox{E}\fbox{F}}$$で赤か青で点灯しなければならないですよね。でも、点灯しませんから、$${\fbox{A}\fbox{B}\fbox{G}}$$のどれかを取ればいい事になりますね。
23.$${\fbox{A}}$$と$${\fbox{1}}$$。
この問題でポイントになるのは、$${\fbox{6}}$$は裏返す必要がないという事です。
なぜなら、$${\fbox{6}}$$の裏が子音なら、そもそも裏返す意味がないですよね。そして、裏が母音でも成り立っていることになるので、確かめる必要はないのです。
しかし、$${\fbox{1}}$$は確かめなければなりません。
裏が母音の場合、表が奇数だという事になってしまうので、『母音が書かれたカードの裏には偶数が書かれている』というルールに反してしまうからです。
$${\fbox{A}}$$は言うまでもありませんね。
24.同じ。
本当に同じなのかを証明してみましょう。
Aのミルクの量を$${a(g)}$$、Bのコーヒの量を$${b(g)}$$、AからBに移した量を$${p(g)}$$とします。
AからBにミルクを移すと、Aの中のミルクの量は$${a-p(g)}$$。
Bの中のミルクの量は$${p(g)}$$、コーヒーの量は$${b(g)}$$になります。
Bから同じ量だけAに移すと、
Bの中のミルクの量は$${p-\dfrac{p}{b+p}\times{p}=\dfrac{bp}{b+p}(g)}$$。
Aの中のコーヒーの量は$${p\times{\dfrac{b}{b+p}=\dfrac{bp}{b+p}}(g)}$$。
なので、同じになるのです。不思議ですよね…。
25.風がある方が時間がかかる。
同じになりそうですが、風がある方が時間がかかります。
それを証明したいと思います。
AB間の距離を$${x(km)}$$、飛行機の速さを時速$${p(km)}$$、AからBに向けて吹いている風の速さを時速$${a(km)}$$とします。
ただし、$${a,p,x>0,p>a}$$とします。
そうすると、無風の場合、$${\dfrac{2x}{p}}$$時間…①
風がある場合は、$${\dfrac{x}{p+a}+\dfrac{x}{p-a}=\dfrac{2px}{p^2-a^2}}$$…②
ここで、➀と②の大きさを調べます。
➀-➁>0なら無風の方が時間がかかり、➀-➁<0なら風がある方が時間がかかることになります。
$${\dfrac{2x}{p}-\dfrac{2px}{p^2-a^2}=\dfrac{-2a^2x}{p(p^2-a^2)}}$$…➂。$${p>0,a>0,p>a}$$なので$${p^2-a^2>0}$$より、➂<0となります。
なので、風がある方が時間がかかるのです。
不思議ですよね…。
26.117
Aが与えられた数を$${a}$$、Bが与えられた数を$${b}$$、cが与えられた数を$${c}$$とすると、
$${a+b+c=9}$$、$${a≦b≦c}$$を満たせばいい事になります。
この条件を満たす組み合わせをすべて書き出してみましょう。

この中ですぐに分かってしまうものは青文字なので、これは省かなければなりません。
次に、AもCも分からなかったけどBが分かったという事を考えてみます。
ここで、Bがどの数を与えられていたかを考えてみましょう。
なぜ、Bは3ケタの番号が分かったのでしょう?
実は、答えは簡単で、Bが『1』をヒントとして教えられていたためです。
例えば、Bが『2』を教えられていると『0,2,4』『1,2,6』『2,2,5』で悩んでしまうはずですよね。
でも、すぐに番号が分かったという事はBが『1』を教えてもらっていたからです。
つまり、Bが牢獄から出ることで、3人とも『117』だという事が分かり、AもCも出ることができるという訳ですね。
27.100m走の2位はC。
何競技あったのか分からないので、$${w}$$競技あったとします。
すると、$${w(x+y+z)=22+9+9=40}$$になります。
$${w}$$と$${x+y+z}$$は40の公約数になることと、
$${w≧2,x+y+z≧6}$$を考えると、$${x+y+z=8,10,20}$$のみです。
ここからは、場合の分けて可能性を探っていきます。
(1)$${x+y+z=8⇔w=5}$$のとき
このときは(5,2,1),(4,3,1)の2通りしかありません。…①
(2)$${x+y+x=10⇔w=4}$$のとき
このときは(7,2,1),(6,3,1),(5,4,1),(5,3,2)の4通りあります。…②
(3)$${x+y+z=20⇔w=2}$$のとき
このときはパターンは沢山あるのですが、Aの条件を2回の試合で満たすことが明らかにできませんので、考える必要はありません。
さて、ここで少し視点を変えます。今までは得点を中心に見ていましたが、今度は『試合数』にスポットライトを当てて、Bの条件を満たすことを考えてみます。
(ア)$${w=4}$$のとき
Bは[6(槍投げ),1,1,1]で9点にするしか方法がありません。
つまり、(1位6点、2位3点、3位1点)です。
これを表にしてまとめてみます。

この場合、Aの赤枠の中にそれぞれ6点を入れなければなりませんが、AもCも満たすことができませんよね。ですので、$${w=4}$$ではなかったという事になります。
(イ)$${w=5}$$のとき
Bは[5(槍投げ),1,1,1,1]で9点にするしか方法がありません。
つまり、(1位5点、2位2点、3位1点)です。
これを表にしてまとめてみます。

すると、Aの条件を満たすためには赤枠にする必要があるので、自然とCの得点が決まってきますので、100m走の2位はCという事が言えそうです。
28.7月16日。
ヒント➀:トムは『ジェリーも分からない!』と断言した
ヒント➁:その後、ジェリーはトムの言葉を聞いて分かった
ヒント➂:しばらくしてトムも分かった
とヒントを整理して考えたいと思います。
ヒント➀から、ジェリーも分からないと断言したということは、5月でも6月でもないという事が分かります。
なぜなら、もし仮にジェリーに18日、19日の情報が与えられていたら、分かってしまうので『断言』はできないのです。

つまり、とらねこの誕生日は7月か8月ということになります。
つぎに、ヒント➁についてですが、ジェリーが分かったのは、15日、16日、17日のいずれかを教えてもらっていたからです。
なので、7月16日、8月15日、8月17日の3日に限定することができます。
最後に、ヒント➂についてですが、トムが分かったは、教えられた誕生月が7月だったためです。
もし、8月を教えられていたら、8月15日か8月17日のどちらかは分からないですよね。
つまり、7月16日だったという訳です。

29.必ず1人は監視されていない囚人がいる。
囚人の人数は奇数なので、$${2m+1}$$人いたとします。
互いに最も近い囚人を監視しなければならないので、この場合、最大で$${2m}$$人の囚人が監視し合っていることになります。
よって、$${(2m+1)-2m=1}$$となり、1人だけ監視されていない囚人がいることになる。
例えば、3人のときを考えてみましょう。
このときは、1人だけ監視されないですね。
次に、5人で考えてみます。

5人の場合でも、1人だけ監視されていないようです。
7人でも試してみましょう。

やはり、1人だけ残るようです。
では、一般的に考えてみましょう。
囚人同士が監視し合っている組が$${m}$$組あったとします。
そうすると、監視し合っている囚人の人数は$${2m}$$人いることになりますが、囚人の数は奇数なので、どうしても1人だけ余ってしまうのです。
つまり、何人になっても、1人だけ監視されていない囚人がいることになりますね。
30.70
実はこの問題、最初から35か70の2択の問題だったのです。
その理由を解説したいと思います。
とらねこはこんなことを発言しています。
『よく聞いていればわたしの持っている数が分かるのですが…。』
これはつまり、全ての質問の答えを聞けば、とらねこがもっている数が分かるという事です。
言い方を変えれば、数を1つに絞ることができるという事になります。
この質問の○、×の組み合わせを考えると、次のことが分かります。

この場合だけ、答えを1つに絞り込むことができるのです。
そして、これらの質問のうち、1つだけ聞き取れたという情報を考えてみましょう。
一体、何で割り切れると聞き取れたのでしょう…?
それは、『2で割り切れる』というものです。
あなたの側にいる人は、2で割り切れるという事を知っていたから『70』と限定することができたのですね。
#とらねこ #英語 #数学 #歴史 #勉強 #理科 #クイズ
#勉強方法
いいなと思ったら応援しよう!

