
フェルマーの最終定理|数学に魅了された人物たちの話
どうも、草冠です。
今回はがっつり数学の話をしていくよ~。
でも別にそんなややこしい事を言うつもりはない。
理解するのも難しいし、そもそも僕自身の理解も危ういものがあるからね。
だから、中身の話よりももっと人間ドラマの部分を話していこう。
「数学と人間ドラマ?」
ってなるかも知れないけど、数学の歴史は本当にドラマになるんだよ。
そのなかでも今回取り上げるテーマがこれだ。
「フェルマーの最終定理」
皆さんはこの定理をご存知だろうか。
最近、何やらドラマでフェルマーの名前を冠する番組が話題らしいので、中身を知っていなくても、「なんか聞いたことある」と思う人も多いかもしれないね。
フェルマーという人物は確かに天才だ。
実績も凄まじい。
だけどね、僕、思うんです。
この人はほんっとうに底意地の悪い人だったんじゃないかなって。
何でそんな風に思うのか、ゆっくり見ていこうか。
ちなみに今回は物語を自由に想像して欲しい。
だからいつも申し訳程度に入れている生成画像の挿入は今回はしない事にする。
フェルマーが残した最後のメモ
生前も数学界に多大な貢献を行ったフェルマー。
彼は最後にあるメモを残してからこの世を去ってしまいました。
1665年の事です。
どんなメモなのかというと、

という内容。
この式だけ簡単に説明しておこう。
君は義務教育で習う、三平方の定理って覚えているかな?
優秀な君ならすぐに答えられるかもしれないね。

この式であらわされる定理の事で、よく直角三角形の問題で利用される。
30度の角を持った直角三角形の辺の長さは
1:2:√3
の比率に絶対になる。
もう必ずなる。
間違いなくなる。
これは三平方の定理で決められた自然の摂理と言ってもいい。
この定理に近いようだけど、フェルマーが言おうとしたことは全く違う内容だった。
n=2 まではこの式は成り立つ。
実際に三平方の定理があるからね。
でも、n=3 から、この式は成り立たなくなるというのだ。
正確には、
「nが3だろうが4だろうが1,000だろうが10,000だろうが成り立つX,Y,Zの組み合わせは絶対にない」
っていうんだよ。
n=2 の時は成り立つのにだよ?
「本当に?」って思わない?
でもあの天才フェルマーがどうやら絶対に存在しないと確かにメモに残している。
おまけにメモにはこんな事が書かれていたらしい。
「私はこの定理について真に驚くべき証明を発見したが、ここに記すには余白が狭すぎる。」
「…はぁ!?」
って当時の数学者たちはなっただろうね。
「いや、オマっ、わかってるんならしっかり証明残してからs…」
とまぁそこから先の発言はnoteにふさわしくないだろうから止めさせてもらったが、
世の数学者たちはきっとそんな風に思ったに違いない。
証明を思いついた事がウソか誠かはわからない。
だけどそのメモは明らかにフェルマーから世界の数学者に対しての挑戦状だったわけだね。
うん、フェルマーのしたり顔が目に浮かぶわ。
見たことないけど。
そうして、世界中の数学者たちはこの定理を
「フェルマーの最終定理」
と呼び、その定理を証明するのに躍起になった。
多くの数学者は文字通り命を懸けて証明に明け暮れてた。
そうやって、結果的には1995年(つい最近)に「証明できた!おめでとう!」って事になるんだけど…
実に300年以上もの間、数学者たちの人生を狂わせた。
「文字通り命を懸けて」と言ったのは、本当に証明することなく亡くなってしまった数学者が沢山いたから。
そう考えると、フェルマーの最終定理が書かれたメモは「悪魔のメモ」のように思えてこない?
それをしたり顔で綴るフェルマー。
底意地が悪いどころの騒ぎじゃないレベルかもしれないけど。(笑)
皆はどう思う?
着実につながれていくバトン。
まぁあんまりにもフェルマーが悪く映ってしまうとかわいそうなので、一応フォローをしておきましょう。
後出しばっかりで恐縮ですが、実はフェルマーはメモにある事も書き残していた。
それは、n=4 の時には成り立たない事の証明だったんだ。
「数字なんて無限にあるのに4の時だけ証明残すとか、ケチすぎん!?」
って思っちゃいますよね。
うん。
少なくとも僕はこのエピソードを聞いたときは絶対に友達になりたくないと思いました。
全然フォローにならなかったな。
ただ、これまた数学界の天才、レオンハルト・オイラーという人物が、この証明を元にn=3 の時の証明をした。
ちなみに蛇足だが、オイラーの残した功績はこれよりも、「世界一美しい等式」とさえ言われる「オイラーの公式」を発見した事が有名だ。
話を戻すと多分、当時の数学者にとってこれは本当に快挙だったんだと思うよ。
「どんどん証明進めていくぞ~!」ってな感じで更にガブリエル・ラメやペーター・ディリクレという人物らが n=5、7、14 の時に成り立たない事を証明した。
ちなみに、オイラーが活躍したのは1700代中頃、その後のラメやディリクレは1800年代中頃。
フェルマーが死に際に残したメモにn=4の時の証明があり、
そこから100年して天才オイラーがn=3の時を証明して、
そしてまたそこから約100年後に新たな天才たちがn=5、7、14の時の証明を行った。
「…えっ?そんだけ?」
って思った?
そんだけ凄い事だったんだよね。
証明をした事も、フェルマー自身も。
一方で、数字は無限にある。
しらみつぶしに証明していくにしても、キリがないからこの命題の証明方法にもブレイクスルーが必要だと思われ始めていた。
その後、100年は動きはなく、20世紀になっても今世紀中の証明は無理だと考えられていた。
1600年代の人間が考え付いた定理だよ?
日本じゃ徳川家康が関ヶ原の戦いに勝って江戸幕府開いてた時ぐらいの話じゃないの。
僕の感覚で言ったらあれだよ、日本人がようやく原始人から人間になり始めたくらいの時期だよ。
…言い過ぎか。
って考えたら本当に凄くない?
未来人かよ、フェルマー…
20世紀中の証明は無理だと言われていた「フェルマーの最終定理」。
でもさっきも言ったけど、実は1995年に滑り込みセーフで見事証明して見せた。
そう、多くの数学者がこの最終定理の証明に挑戦しては敗れ、挑戦しては敗れを繰り返していたわけだけど、ただ敗れるだけではなかった。
その研鑽を、バトンに込めて次に次にと託し、とある日本人の手に渡った時、ブレイクスルーが起こった。
2人の天才日本人数学者
その人物は、谷山豊という人物。
ちなみに、読み方は「ゆたか」ではなく「とよ」が正しいらしい。
初見殺しだね。
ただ、印象としてはバトンが渡ったというより、
「谷山氏がまた新たにバトンを作り出した」ってイメージの方が近いかもしれない。
と言うのも、彼もまた、まぎれもない天才数学者であり、彼が残した功績はある突飛なアイデアを残したことにあった。
それは「すべての楕円曲線はモジュラーである」というもの。
…もうこんなのは意味が分からなくてもOKです。
少し話はそれますが、彼が活躍した頃の時代背景は、戦後の日本。
完全に熱意がそがれ、研究はおろか生きる事でさえ必死の状況。
そんな状況ではあるけども、周りも気にせず自分の好きなこと、気になる事を追求する人たちはやっぱり一定数居ます。
世間的に見れば「空気の読めない奴ら」として見られそうですが、そうした要素が天才性には必須なんでしょうね。
谷山氏もそのうちの一人だった。
ある時、数学研究のシンポジウムが日本の日光で開かれる事があって、
日本の若手数学者たちが、
「これは自分の研究を世界に知らしめるチャンスだ」
と見て、それぞれの研究をまとめた文書をその場にいた世界中の研究者たちに配布したそうです。
この時の文書の中に、谷山氏の意味不明なアイデアが含まれていた。
ですが所詮は敗戦国の日本、しかも研究者としてはまだまだ若者である彼らの主張は先進国の研究者たちから大した評価は得られませんでした。
特に谷山氏の提言は、「何を言ってるんだコイツは」と、僕らほど意味不明の状態ではないと思いますが、「現実的ではないアイデア」として一蹴されたそうです。
なかなか厳しい世界ですね。
そうして理解を得られなかった谷山氏は、なんと31歳の若さで自殺をしてしまいます。
動機は不明だそうですが、とにかく悔やまれますね。
彼がもしも生きていたら、また世界は違った姿になっていたかもしれません。
ただ、彼の友人である志村五郎という人物が彼のアイデアの根拠となる部分を明確にしました。
サラッと言っちゃいましたが、実はコレ、大変凄い事なんです。
だって当時の最先端を走っていた研究者が「現実的ではないアイデア」と評していた考えを現実的にしたって事ですからね。
このアイデアを二人の名字を取って「谷山-志村予想」と呼ばれています。
「○○予想」というのは、「○○定理」の予備軍みたいなもので、「証明はできていないけど、9割9分これは正しい」と言えるものをそう言います。
そして、ドイツのゲルハルト・フライという人物が、この「谷山-志村予想」に注目した。
「フェルマーの最終定理」の最後
改めて「フェルマーの最終定理」と「谷山-志村予想」がどんなものだったかを整理しよう。
- 「フェルマーの最終定理」
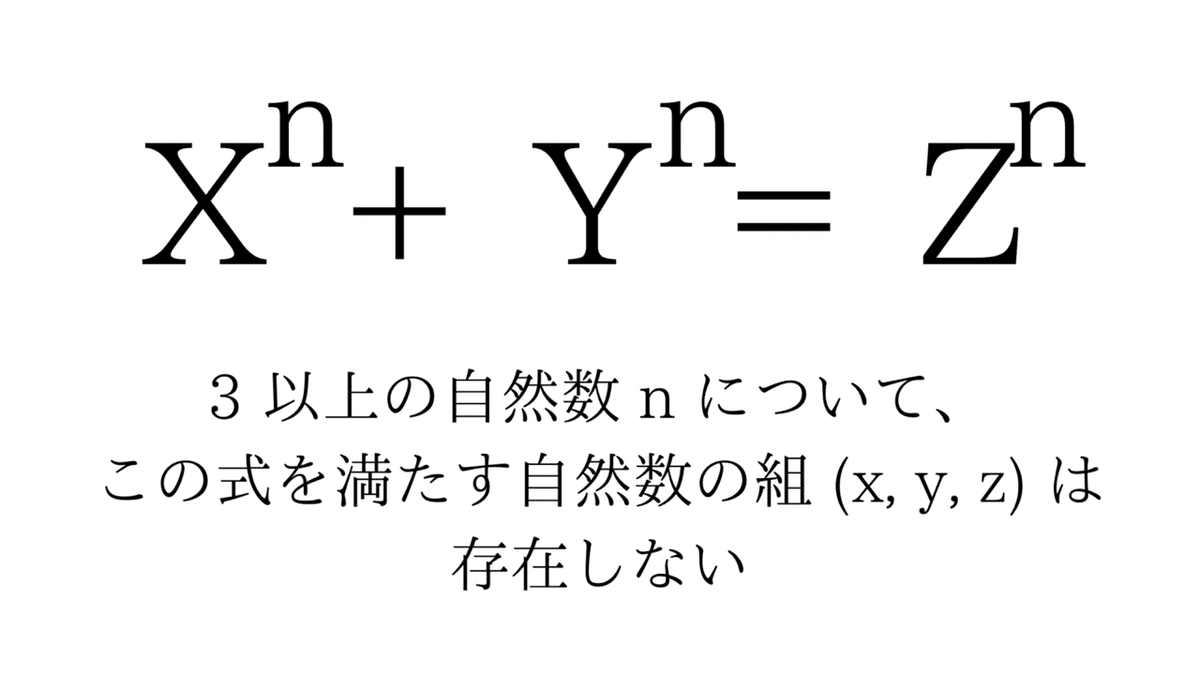
この式が成り立つn=3以上の自然数はないという事だね。
4とか5とか、一個一個の証明はできているものの、数字自体は無限にある。
その全てにおいて証明はまだできていない。
「もしかしたらあるかもしれないよね」という悪魔の証明状態。
- 「谷山-志村予想」
「すべての楕円曲線はモジュラーである」
よくわからない。(笑)
でも要はこの楕円曲線が「モジュラーである」って事に誰もその当時結びついていなかったわけだ。
先ほど新たに登場したフライ氏は、
もしも「フェルマーの最終定理」でn=3以上で成り立つ自然数があったとしたら、それは楕円曲線にはなるけど、モジュラーにはならない
と考えた。
難しいね。
わかりやすくしようか。
『楕円曲線になる事を”A”』として、
『モジュラーになる事を”B”』としてみよう。
じゃあ、「谷山-志村予想」が言っているのは
【 A なら… B になる 】
という事だ。
だけどフライ氏が指摘したのは、
もしもn=3以上の自然数でフェルマーが提示した式が成り立つと仮定したら
【 A になるけど… B にならない】
という事だった。
だから、「谷山-志村予想」を証明する事が出来たら、さっきの仮定は矛盾しているという事になり、
晴れて「フェルマーの最終定理」が証明できたと言えると、フライ氏は考えたんだね。
ただ「谷山-志村予想」の証明も一筋縄じゃ行かず、
この証明が20世紀中には無理だって言われてたんだけど、これも世界中の天才を集めて1995年、証明に成功する事が出来た。
こうしてあのしたり顔フェルマーに最後の一撃をくれてやる事が出来たわけだけど…
一体どれだけの金と、人と、時間が費やされたのだろうね。
想像もできん。
最後に
いかがでしたでしょうか。
悪魔の証明、「フェルマーの最終定理」を巡る360年にわたる数学者の戦いの歴史を誰でもわかるように簡単に、でも深くのめりこめるように、そんな風になるように書いてみました。
番組表を見ていると、ドラマ枠でしれっと「フェルマー」なんて単語をタイトルに使用しているのを見て、
「その言葉の重みを知ってんのか!?」
なんて思ったりもしたけどね、まぁ言葉の受け取り方は人それぞれですから。
この記事を読もうと思った言葉好きのnoter達にはぜひ、「フェルマー」という言葉の歴史と言いますか、何があったのかくらいはわかってもらえたらいいなと思います。
ドラマもこれを知るともっと面白くなるかも!?(見てない)
前回の記事はこちら
