
「ピタゴラスの定理」は5000年以上前の縄文時代の粘土板にも記されているのか
引用します----ーーーーーーーーーーーー 縄文遺跡である秋田県鹿角市の大湯環状列石遺跡から数を示す土版がみつかっている。タブレットとはメソポタミアで陶板を示すものであり、大湯環状列石遺跡から出土の数を示す土版は現在のタブレット端末より一回り小さいスマートフォンほどの大きさである。壊れにくくするために厚みはある。
大湯環状列石遺跡から出土の数を示す土版には1、2、3、4、5を示す穴があけてある。その配置は見事といってよい。形状は人の顔と身体に似せている。1が口で2が目と思われる。
数を数えるのに土に線を引いてもよい。数にあわせて石をならべてもよい。紐(ひも)に結び目をつけてもよい。腐るものは残りにくい。刻んだ月日の移行を示す骨が残されている。夏至と冬至などを知っていることを示すのが英国におけるストーンヘッジである。
大湯環状列石遺跡から出土のタブレット状の土版には1、2、3、4、5を示す穴があけてある。この数字を示す穴を使って足し算や掛け算をしたことであろう。頭の中に思い描くよりも土版の数字を使えば計算がしやすい。
長さの基準となるモノサシを使って倍数を刻むことが三内丸山遺跡の遺構から確認されている。モノサシは35㎝であった。目盛りを刻んであったかどうかは別だが目盛りを刻むことはたやすい。巨大建築物の柱の間隔は4.2mになっている。柱を埋めるための穴は幅と深さが2mである。統一したようにそのようになっている。
数を示す土版は大人の計算機であったろうが、子どもに数と計算を教える道具であり教科書であったことが想定される。 ーーーーーーー引用終わり
このように説明されている土版です。

図 土版の表面
左から3,5、4 の数が記録されている
その下部には正方形が書かれている
これは三平方の定理を示しているとしても良いのではないだろうか
それは飛躍しすぎという方は次を見て貰いたい。
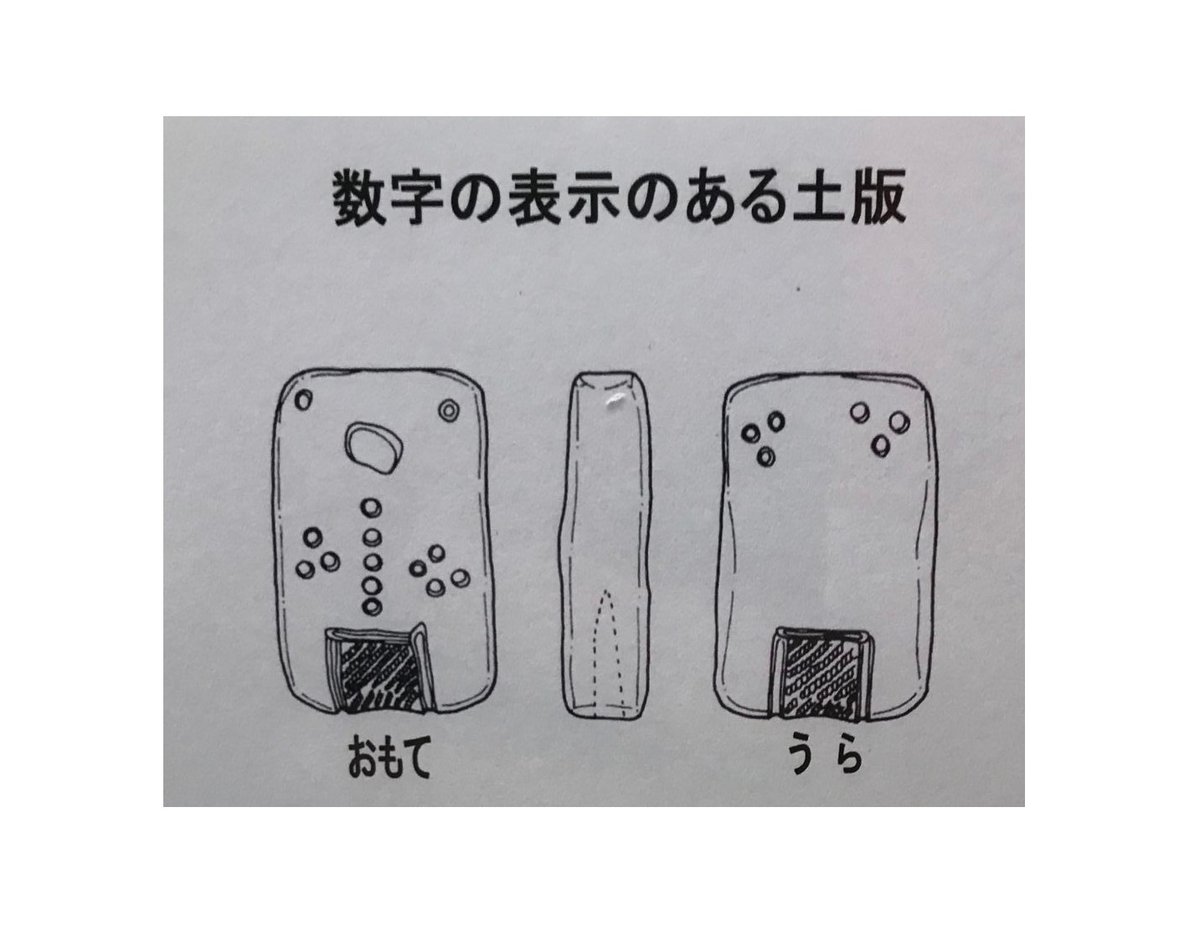
図 裏面の3と3 そして下部にある正方形
これは計算法を示しているとして良いのではないだろうか
ここに 3掛ける3 を例示して正方形を示していて、
表面を見れば、4、5への正方形計算の拡張を暗示していたことが分る。
これは石ころで列べれば直ぐに理解出来る整数計算なので、このくらいのことは分っていたのではと思う。
土器・粘土板は、第三の道具でもあり、メディアである。情報伝達の用途に使われていたという、新石器時代の土器の意味するものを明確に示している例である。
引用します----ーーーーーーーーーーーー
「ピタゴラスの定理」はピタゴラスが生まれる1000年以上前の粘土板にも記されている
c GIGAZINE 提供
「2辺(a、b)上の2つの正方形の面積の和は、斜辺(c)上の正方形の面積に等しくなる」という三平方の定理は、「ピタゴラスの定理」とも呼ばれ、古代ギリシャのピタゴラスが発見したとの逸話が残されています。しかし、ピタゴラスが生まれる1000年以上前にバビロニアで作られたとされる粘土板に、三平方の定理について記されていたことが明らかになっています。 Pythagoras: Everyone knows his famous theorem, but not who discovered it 1000 years before him | Journal of Targeting, Measurement and Analysis for Marketing https://link.springer.com/article/10.1057/jt.2009.16 The Pythagorean Theorem was discovered by the Babylonians 1000 years before Pythagoras was born
東アジア地域でのピタゴラスの定理の状況は次のような説明があります。
3,4,5 の三平方の定理の起源は明確にされていない。ということは、縄文時代の起源であることは、{想定内}に入れても良いのでは無いか。
3,5,4 について
「数の日本史」2002年 伊達宗行 から引用します
引用します----ーーーーーーーーーーー--


