
微分とか何の意味あるん?(4)
微分シリーズの4回目でございます。ここまでの流れは下の図のようになってます ↓

前回の記事はこちら ↓
今、書こうとしているのは、微分の計算でやっていることは傾きの計算であることを示すことです。
その一環で、前回の(3)では、微分の定義を紹介しました。これですね ↓
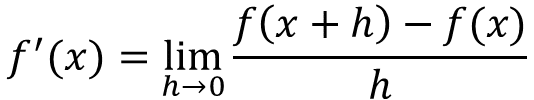
前回はこの式を登場させるだけで終わってしまったので、今回は実際にこの式を計算をして、(1)の時に微分の公式で盲目的に計算した結果と一致することを確かめていこうと思います。
今回は、結構計算をひたすらやる回です。計算式が苦手な方は、なんとなく眺めて流し読みしてください。
でも、できる限り分かりやすく書いてますよ♪
もちろん、f(x) には、(1)で用いたのと同じ式をあてがいます ↓

(1)で、上の式の微分の計算は既に行ってます。こうなるはずです。

これを先ほどの微分の定義式から計算して、↑ と同じになるかやってみましょう。え?何から手を付けていいかわからないですか?
心配ありません!代入するだけです。

【?】の部分はこれから考えるんですが、ひとまず代入するべき部分を図示してみました 。f(x) のところは全く問題ないですね。
では、 f(x+h) というのは、どうしたらよいでしょうか?前回、f(x) の説明をした時のことを考えれば簡単です。
例えば、x=0 の時の f(x) というのは、こうなりましたね↓

これと同じやり方をします。x を x+h に置き換えて計算すればOKということです。
![]()
この後、f(x+h)-f(x) という引き算をやらないといけないので、()は展開してしまいましょう。こうなります ↓

これで分数部分の準備が整いましたので、微分の定義式の赤い四角の部分を計算していきます ↓

代入するだけなので、こんな感じ ↓
![]()
そのまま引き算を計算していきます ↓

この計算結果を、微分の定義式に反映させます ↓

こうなりますね ↓

さていよいよ lim を計算するタイミングが近づいてきました。lim とか手ごわそうでしょ?でも、意外と大したことはありません。手ごわそうでしょ?でも、意外と大したことはありません。
例えば、

計算すると、

意外とあっけないでしょ。lim というのは、x が 0 に究極的に近づく時どうなるかという計算です。「究極的に0に近づく」というのは要するにどういうことかというと、x=0 に決まってます。
どうですか?急激に lim が雑魚っぽく見えてきたのではないでしょうか。
雰囲気に負けちゃいけません。lim とか、実体は大したことないのです!
h→0 とあるので、「分母が0になってしまうじゃないか!」と心配する方もいるかもですね。でも心配いりません!なぜなら実はこれ、約分できます。
なので、lim の計算は、約分した後でOK!
なので、計算するのは ↓ となります。

(実質的に)h=0 を代入すればよいので、ah の部分はなくなり、
結果、f'(x)=2ax+b となりました。
まとめ
いかがでしたでしょうか。今回は、微分の定義からじっくり計算し、確かに微分計算の公式の結果になることを確認しました。
次回は、(3)(4)で示した、微分の定義が、(2)でお話しした傾きの計算そのものであることを示していきます。
長々と計算にお付き合いいただき、ありがとうございました。
この記事の上位テーマは ↓ です。よかったらアクセスしてみてください。
