
マトリックス推理パズルの解き方・初~中級編
この記事は、ペンパアドベント2023の2日目の記事です。
以前筆を執ったものの途中で放置していた、推理パズルのお話。
一口に推理パズルといっても色々なタイプがありますが、その中でもニコリ本誌でメジャーな「マトリックス型」固有の解き方の話です。
特に、らくらく問題から大サイズの難問に至るまで、どんな問題でも常に使い続けることになる基本操作「転写」について触れていきます。
1.転写について
そもそも「転写」はどういうものなのか。これは自分が勝手につけている用語なので、世に浸透しているものではありません。ですが、推理パズルをある程度解いた経験がある方なら、息を吸うように行っているであろうアレです。
1.すでに、盤面にいくつかヒントが入っていたとします。

2.新たに○がつけられました(赤い○)
ここで、新たな○マスと同じ行・列にある、別の部屋のマス(赤いマス)に注目します。

3.これらのマスには、○マスを経由する形で、かならずどこか別のマスが1対1で対応しています。
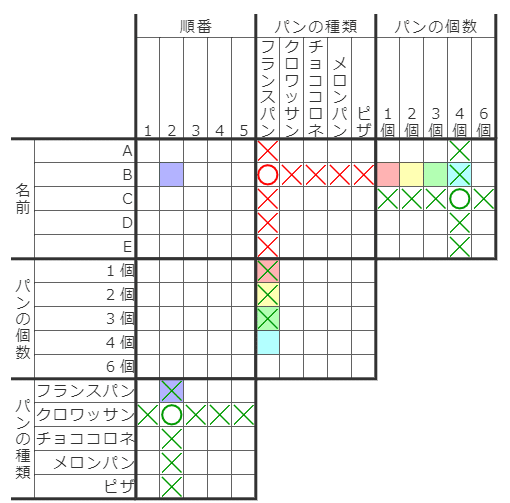
例えば、上の図の赤・黄・緑・水色のマスのペアはそれぞれ「B=フランスパン」という関係によって、「Bが買った個数=フランスパンの個数」と論理的に同値なマスになります。
4.1対1対応するペアのどっちかが確定済みマスなら、もう片方のマスもそれで確定します(青い×マス)。

転写の操作を行うことで、問題文では直接示されないマスについて何も考えず機械的に×を埋めていくことができ、ぐっと解き進めやすくなります。
以下、具体的に「右下・上・左」の3つの方向の転写について、それぞれ例を見ていきます。
1-1.右と下の転写
最もやりやすいタイプで、特に小・中サイズでは基本となる転写です。
「〇」が入ると、その右側または下側の部屋の×の並びが、そのまま下/右の対応する部屋と揃うように入ります。
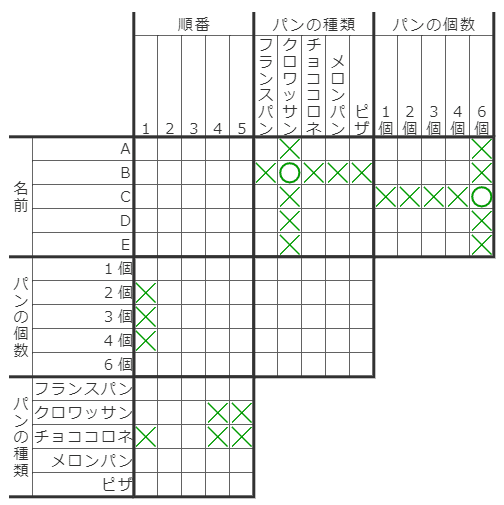

例えば、一番左の列で「パンの個数=2,3,4」に×がついていますが、赤い○について転写を行うことで、一番上の行の「パンの個数=2,3,4」にも×がつけられます。逆に、この行には「パンの個数=6」にも×がついているので、一番左の列の「パンの個数=6」にも×が新たにつけられます。
結果として、A(1番目)のパンの個数は1個だと確定することになります。このように、転写で×を漏らさずつけていき、空きを残り1マスにして○を確定させていくのが推理パズルの基本パターンです。
1-2.上の転写
「○」の上側にあるマスは、どのマスと1対1対応するのでしょうか。
まず、○の左側の項目名を見て、それと同じ項目名を上から探してきます。その縦列が、○の上側と1対1対応する列になります。
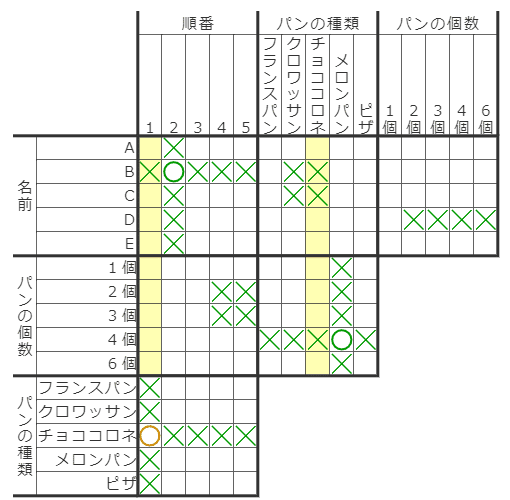
例えば、上の図で黄色の○が新たに入ったとします。黄色○の左側の項目名は「チョココロネ」なので、黄色○の上側のマスは、上側にある「チョココロネ」の項目の列と1対1対応することになります(黄色マス)。
あとは、この2つの列を見比べながら、転写していきます。
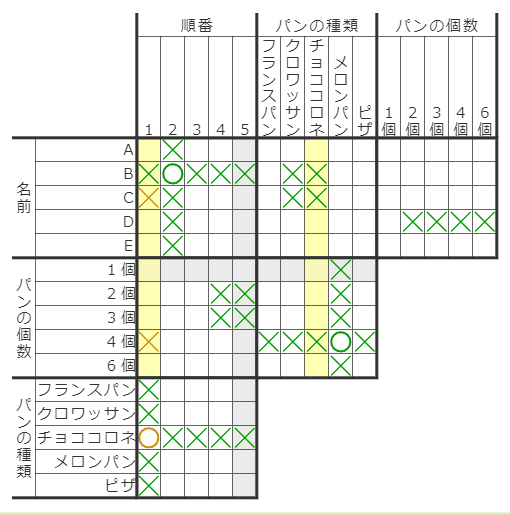
1-3.左の転写
「上の転写」と縦横が入れ替わるだけです。
まず、〇の上側の項目名を見て、それと同じ項目名を左から探してきます。その横行が、〇の左側と1対1対応する行になります。
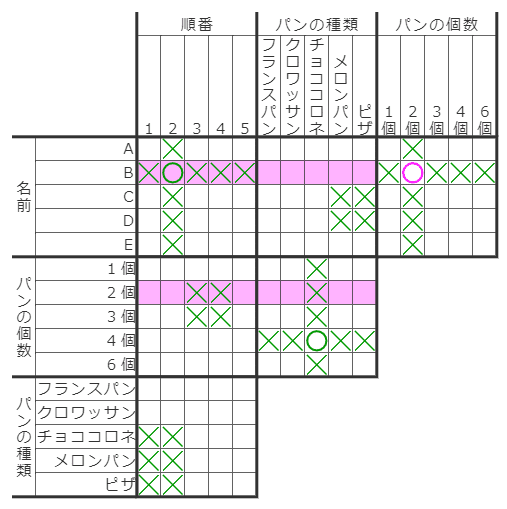
上の図で、新たに紫の○が決まったとします。紫○の上側の項目名は「2個」なので、1対1対応する行は、左側にある「2個」の項目名の行です。
あとは、これら2行(紫のマス)どうし、記号を見比べていきます。

今回のように、×だけでなく○が転写されることもあります。上の図では、そこからさらに右下の転写により、「Bーメロンパン・ピザ」「2個ーメロンパン・ピザ」の計4マスにも×をつけられます。
上の転写・左の転写は大サイズの問題になるほどよく使いますが、見るべき行・列を間違えることが多いので注意。うっかり1つ隣を転写してしまい破綻するのは誰しもが通る道。特に飲酒しながら解いてるとなおさら。
1-4.○の長方形の法則
テクニックというよりも知識ですが、「完成形のマトリックス内では、必ず○が長方形の頂点に位置する」という法則があります。
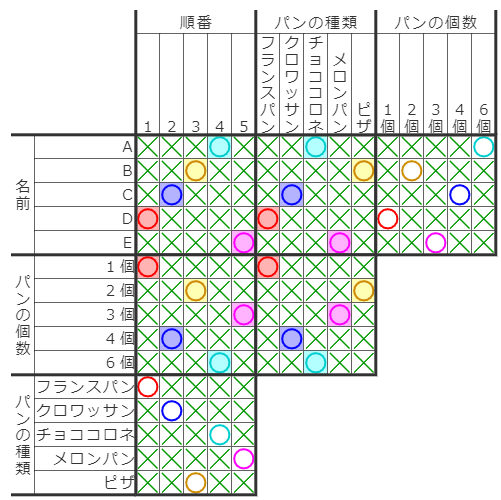
転写やマトリックスそのものの性質を考えれば当然の帰結ではありますが、知っておくと終盤のウィニングランや破綻チェックの際に役に立ちます。
2.確定可能な×マスを常に漏れなく入れる方法
これはテクニックというよりは知見というべきもので、解くうえで必須というものではないです。
推理パズルを解いていて、問題文から直接決まる○×がある程度決まってくると、やがて「現時点で論理的に確定する×マスを全て洗い出す」作業が必要になるかと思います。
ですがこの作業は、○や×が確定する度に以下を行うことでスキップ可能です。(※ちゃんと数学的に証明したわけではないのですが、経験則的に確かだと思います)
・新たに「〇」がついた場合
⇒ そのつど右下・上・左の3方向の転写を怠らず行えばOK
・新たに「×」が単体でついた場合
⇒ 以下の手順をたどることで、同時に確定する他の×マスを洗いだせます。
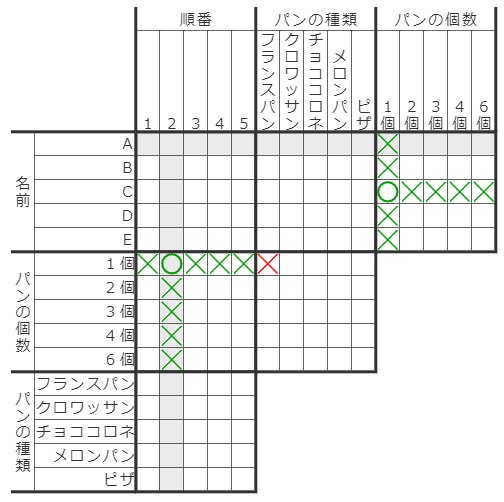
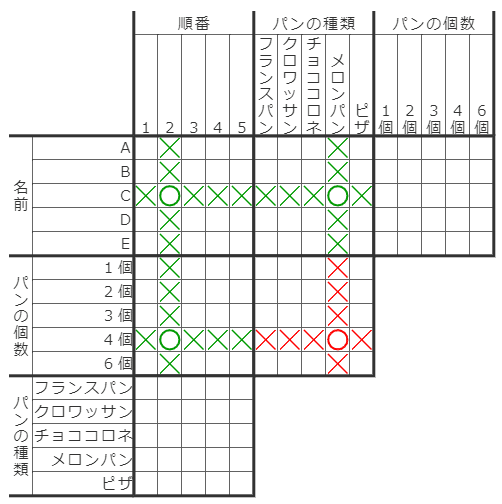
上の緑の○×が確定した状態で、新たに赤い×が確定したとします。このとき、×と同じ行・列、そしてそれらに1対1対応している行・列を全てチェックします。
今回の例では右側と下側に部屋がないので、左側(下図の赤マス)と上側(下図の青マス)がチェックの対象です。
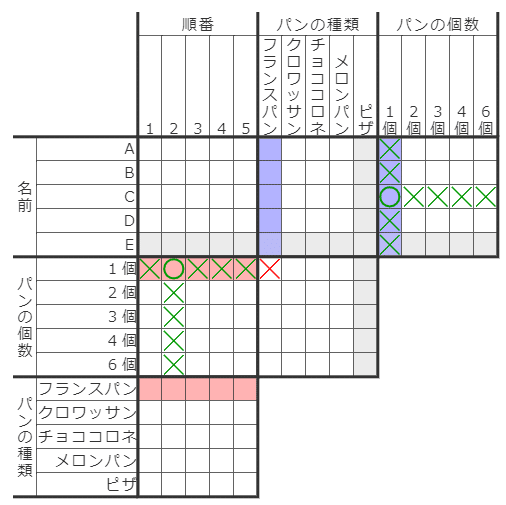
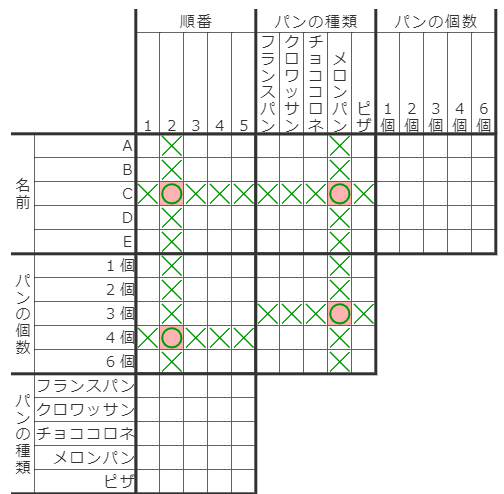
チェック対象のマスに○が含まれていたら、それぞれの○について、最初の×とペアになるマスがあるので、そこに新たに×が入ります。
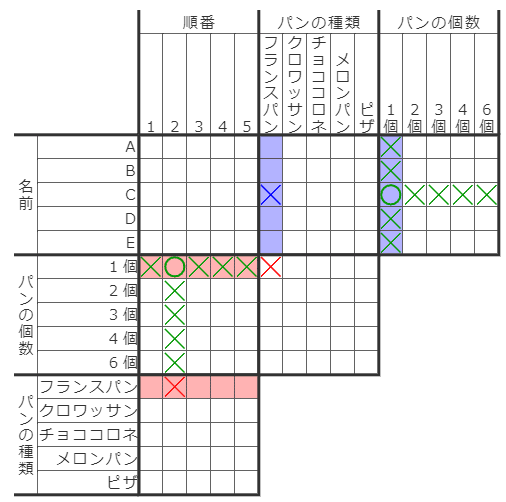
中央部屋の赤×が入ったことで論理的に確定する×マスはこの2つだけです。
もちろん、この節のテクニックは「途中の×の入れ漏らしをなくす」だけで、あとからまとめて転写作業を行えば済む話ではあります。進め方・好みは人それぞれです。
3.そのほかの技法
そのほか、×マスを確定させるためのいろいろなテクニック・手筋集
3-1.どっちにしろ理論
数独でいう井桁理論(X-wing)と同じ手筋ですが、推理パズルではらくらく~おてごろレベルでも普通に使うことがあります。
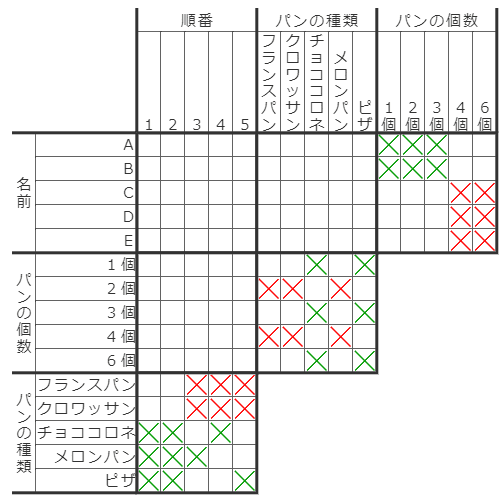
右上、中央、左下のそれぞれの部屋において、緑×が確定した状態で、赤×を確定することができます。
左下の部屋において、横方向の×の並びに着目すれば、3列以上に拡張することもできることが分かると思います。数独でいうソードフィッシュ系の手筋と同じです。
一気に×が決まる、適用できると気持ちよい手筋です。
3-2.強い相互関係をマークする
これはマトリックス単体の形式的操作というより、問題文もちょっと絡んでくるお話。
推理パズルでよく見かける「AはBくんの2倍の数のパンを買ったよ」や「CはDくんの次の番だった」のように、片方の数値が確定すれば他方もリンクして確定する関係のことを、「強い相互関係」と勝手に名付けることにします。
一方で、「AくんはBくんより多くのパンを買った」など、一方が確定しても他方が完全に確定するわけではない関係性を、「弱い相互関係」と呼ぶことにします。
さて、強い相互関係においては「対応するマス間で〇×のパターンが完全に一致する」という性質があります。
例えば「AくんはBくんの2倍の数のパンを買った」というヒント文から、下図の赤マスと青マスでは、〇×の入り方(横の並び)が一致します。
また、ついでにいくつかの×マスもつけられます(Aのパンの個数が1個や3個の場合はありえない、など)。
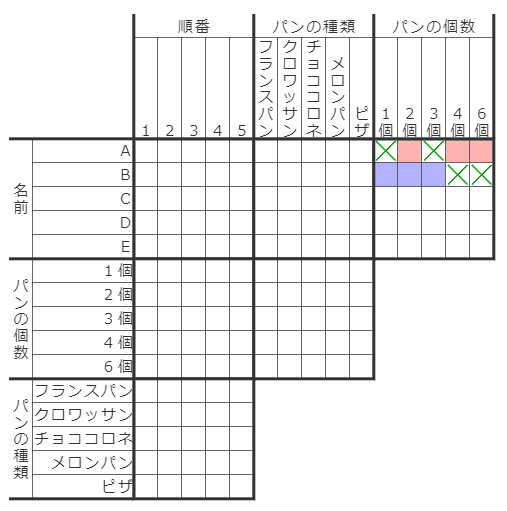
「強い相互関係」を一度図のようにマークしてしまえば、この時点でそのヒントが持つ全ての情報量を使いきったことになります。
つまり、このヒントについてはもう問題文を見返す必要がなくなり、あとはマトリックス上の操作に専念するだけでよくなるのです。
2者間比較系のヒントを言葉のまま扱うのは(少なくとも自分にとっては)脳の負担が大きいので、このようにマトリックス上で何も考えずに操作できる形式に変換することは中々効果があります。
今回はPC用のツールを使っているので色でマークしていますが、紙面で解く場合は線を引くなどしてマークして解いています。
大サイズだと強い相互関係タイプのヒントだけで3~4個はザラに出てくるので、直線・波線・点線・破線などを使い分けて、どれとどれが対応関係があるのか分かるようにしておくとよいです。
また、中級以上の問題だと、強い相互関係とどちらにしろ理論の合わせ技が使われることがあります。例えば、図のように×がついた状況で「CはDの次の番」というヒントがあったとしましょう。
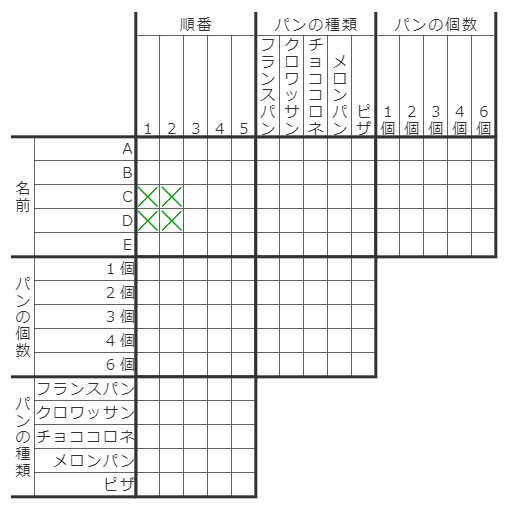
「CはDの次の番」という強い相互関係を、赤色マスとしてマークしておきます(ついでにC-3, D-5に×がつけられます)。
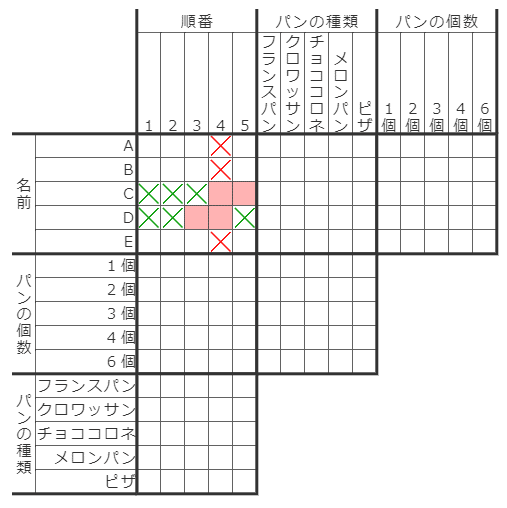
横並びの赤色マスには「○×/○×」か「×○/×○」のパターンのどちらかで入ることになりますが、いずれの場合でも「順番=4」の列においては、赤マスの部分に○がつくことになります。
したがって、上図において赤色の×が確定します。
3-3.背理法(矛盾を見つける)
ヒントも使い切って転写も全部やりきったけど、手詰まりになってしまった。そんな場合は、以下の最終手段で突破できることがあります。
1.適当に空いているマスを一つえらぶ。
2.そこに〇がついたという体で転写を行うと、ある場所で全部×の列ができてしまい破綻する。
3.つまり、そのマスは×で確定する。
いくつか例を見てみます。
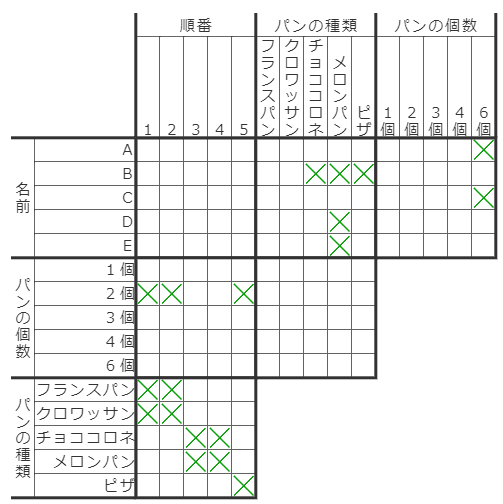
例えば、左上のB-1やB-2に○をつけて転写を行うと、「パンの種類」の部分が全部×になってしまいます。よって、この2マスは×で確定です。

B-2についても同様。つまり赤マス2つはどちらも×で確定。
他にもまだ決まる場所があります。
例えば、中央領域の「2個ーチョココロネ」や「2個ーメロンパン」の部分に○をつけてしまうと、左方向の転写によって「順番」の部分がすべて×になってしまいます。よってこの2マスも×で確定。
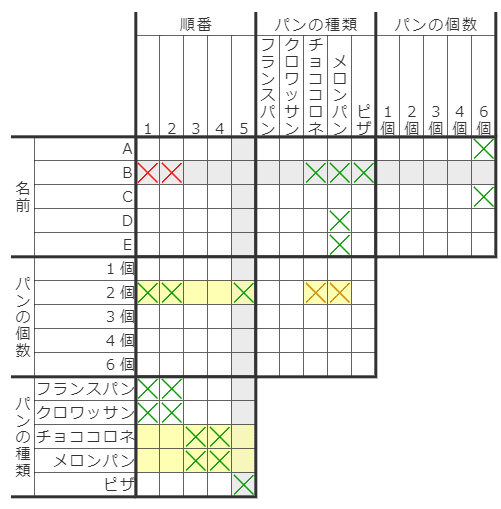
上方向の転写を使う場合も同様です。上のサンプルで、あと1マスだけ背理法で×が確定するマスがあるのですが、お判りでしょうか? (※)
たいへん~アゼンクラスの問題にもなると、これを使わないと解けない問題があったりします。作問中も、ある程度盤面が埋まってきたら、破綻防止のために一度背理法で決まる×マスを探してみるのも手かもしれません。
とはいえ、探しづらいうえにこれで×が決まることはあまりなく(仮にあったとしてもそこから先につながらないケースが大半)、本当に手詰まりしたときの最終手段といえます。
一度マトリックスのことを頭から離して問題を柔軟に整理することで、裏に隠された糸口を見つけられることもあります。
(※)中央部屋、「6個ーメロンパン」のマスでした。
<まとめ>
マトリックス型の推理パズルを解くコツは、とにかく「転写」の操作に慣れることだと思います。
あとは「強い相互関係」に忘れずマークをつけておくこと。脳内で保持する情報量を減らせ、他の推理に集中できるようになります。
他にもっと良い解き方・テクニックがあるのかもしれませんが、自分はこんな感じで推理パズルを普段解いています、というお話でした。
ぜひ、ご参考になれば幸いです。
おまけの推理パズル
<問題はこちらから> たいへんレベル
(※最初に:上で使っている画像と答えは一切関係ないです)
A, B, C, D, Eの5人とFさんがパン屋にいきました。
Fさんの話から、それぞれが買ったパンの種類とその順番、個数を当ててください。
・最初に買ったのはEくんで、フランスパンを買っていたわね。
・4番目にパンを買った人は2個パンを買っていたわ。
・ピザを4個買った人がいたけど、それはチョココロネやメロンパンを買った人よりも前だった。
・チョココロネとメロンパンだと、チョココロネのほうが買われた個数が多かった。
・AくんはBくんの2倍の個数のパンを買っていたよ。でも、Aくんが買っていたのはクロワッサンじゃなかった。
・Cくんがパンを買ったのはDくんの次だったけど、二人とも2番目ではなかったわ。
・それにしても、おなかすいたわ。私もパンを買えばよかった。
<答え>
・A:5番目、チョココロネ、6個
・B:2番目、クロワッサン、3個
・C:4番目、メロンパン、2個
・D:3番目、ピザ、4個
・E:1番目、フランスパン、1個
終盤、左上部屋A-2のマスで背理法を使う想定です(使わなくてすむ裏道もあるかもしれません)
