
Kyle Hendricks投手の試合中のリリースポイントの変化 Part2
前回、Kyle Hendricks投手の試合中のリリースポイントの変化を集計しました。
その際、図の出来に不満があったので今回はこれを修正してみようと思います。
問題の図
修正したい図のポイントは、以下の図のプロットの色です。

これは、リリースポイントの位置を縦と横の軸で表し、リリース時の球速(m/h)をプロットの色で表しています。これはストレート(4-Seam Fastball:FF)のデータですが、プロットの色にほとんど違いがありません。
同じような球速で投げているという可能性もありますが、図の右に示してある球速の幅が広すぎる可能性が考えられます。60m/hから100m/hまで幅をとっていますが、1人の投手の1球種でここまで球速に違いが無いため、プロットが同じような色となってしまった可能性があるということです。
この問題を解決するには、球種ごとの球速の幅に合わせた設定が必要です。
選手間で比較するのか、1人の選手の変化を見るのか
このように、選手に合わせてデータの幅を設定するというやり方は、今回のように1人の選手のデータの変化を追いかける場合には有効な方法ですが、複数の選手間のデータを比較するのには向きません。ある選手に適したデータの幅が、他の選手に適しているとは限らないからです。複数の選手のデータを比較する場合には、ある程度共通したデータの幅が必要になります。
ところで、前回集計したデータは、球速(release_speed)、回転率(release_spin_rate)、打球速度(Launch Speed)の3つです。このうち球速(release_speed)と回転率(release_spin_rate)は投手個人の特性が反映されやすいのに対し、打球速度(Launch Speed)は、打球の角度と合わせてHRになりやすさがわかっており、選手ごとに幅を決めるよりは共通のデータ幅を設定したほうが良いと思います。
というわけで、今回は球速(release_speed)、回転率(release_spin_rate)の2つを、Kyle Hendricks投手に合わせてデータの幅を設定し、改めて作図したいと思います。
Kyle Hendricks投手のデータ幅
まずは、球速(release_speed)の分布を以下の図2-1に示します。

ストレート(4-Seam Fastball:FF)・シンカー(Sinker:SI)・チェンジアップ(Changeup:CH)・カーブ(Curveball:CU)の4球種のデータの分布を確認しましたが、球種ごとの分布はそれほど広くないようです。
次に、回転率(release_spin_rate) の分布を以下の図2-2に示します。
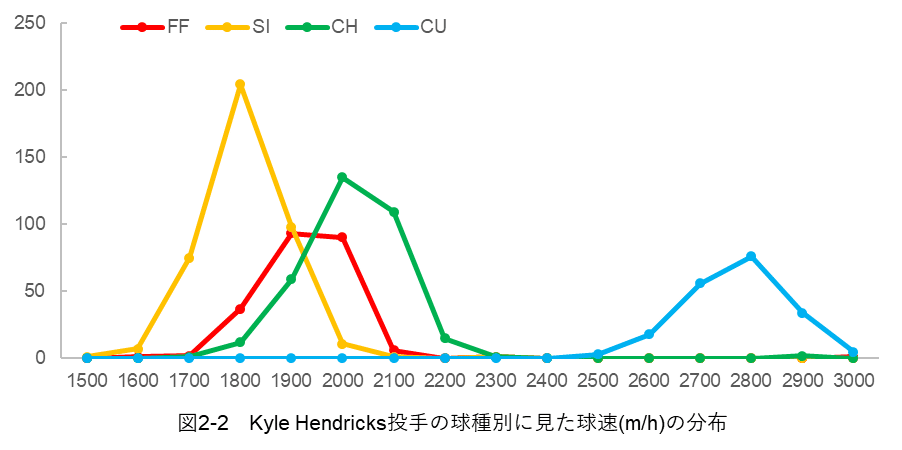
このデータも、そういうものかということで、以下の表1に示すようにデータの幅を設定しました。
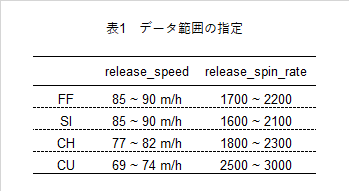
ストレート:4-Seam Fastball – FF
それでは、新たに設定したデータの幅で、リリースポイントと球速(release_speed)の関係を以下の図に示します。

図の見方は前回と同じで、10球ごとのリリースポイントをgifファイルで示しています。縦の軸はリリースポイントの高さを、横の軸は0をプレートの中央に取ったリリースポイントの水平方向の位置を表します。Kyle Hendricks投手は右なので、プロットが左にあるほど、プレートの中央から遠くでリリースしていることを表します。
次に、回転率(release_spin_rate) のデータを下図に示します。

前回の図と比較すると、プロットの色の違いが良くわかるようになったと思います。
シンカー:Sinker – SI
次はシンカーで同様に集計しました。データを以下に示します。

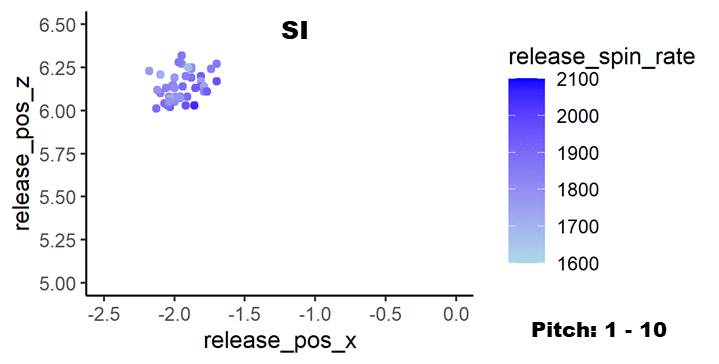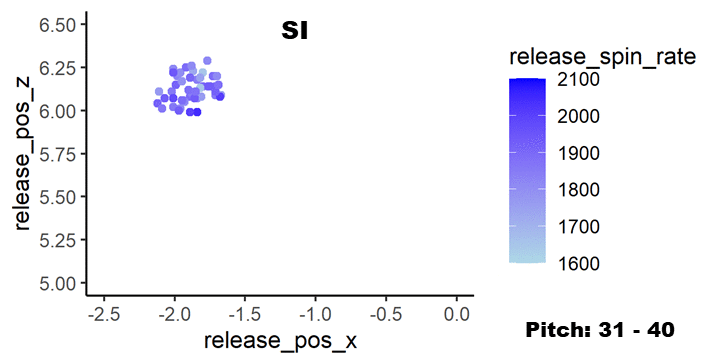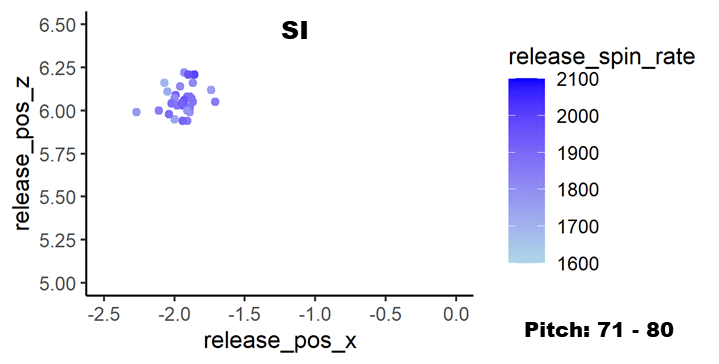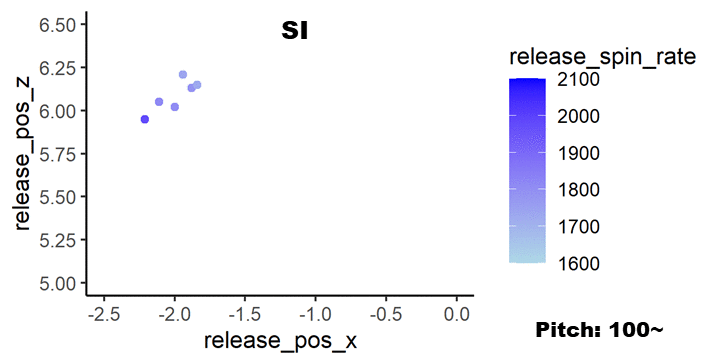
こちらもプロットの色の違いが分かりやすくなりました。
チェンジアップ:Changeup – CH
続いて、チェンジアップのデータを以下に示します。


プロットの色の違いは見やすくなりましたが、リリースポイントとの関係は良くわかりません。
カーブ:Curveball - CU
最後に、カーブのデータを示します。


カーブの場合は、リリースポイントが低いほどプロットが赤い、つまり球速(release_speed)が速いと見ることができます。
まとめ
以上、前回よりはKyle Hendricks投手の特徴が良くわかる図になったのではないでしょうか。
こうした図を作成する際の注意点として、無理に差異を作り出そうとして、データの幅を狭くしすぎることがあります。下手をすると、誤差に過ぎない差異を何か意味のある差と読み間違えてしまう可能性があります。
何事も程々にというわけですが、そのためには図2-1や図2-2で見た分布の確認が重要になります。
タイトル画像:いらすとや
使用データ
https://baseballsavant.mlb.com/
