
動かして学ぶバイオメカニクス#9 〜身体各部の座標系〜
身体に固定された座標系(原点+姿勢回転行列)は解剖学的な関節角度の定義に関係するが,回転の力学で厄介な問題の一つがその座標系の定義である.数理的というよりも,これを決める作業はどろくさく定義が人によって大きく異なるかもしれない.また計測するマーカの配置にも強く依存する.その意味で,ここでの方法は参考にならないかもしれないが,計測環境に応じて自在に座標系を定義できる力を養っていただけたらと思う.
身体座標系(ローカル座標系)の定義
身体各部位のローカルな座標系の定義は,ISB(international Biomechanics Society)が定めた定義(文献1,2)があるが,多くの人がそれに従っているという印象はない.理由としては,特にそれによって大きく計算が異なるわけでもなく,マーカの貼付位置などに強く依存し,設定が異なるからだろう.力学計算では身体各部位の質量や慣性モーメントを定めるモデルにも依存する.特に軸の順番などはまちまちという印象である.そのような観点からすると,計測環境に応じて自在に座標系を定義できる力を養うほうが望ましい.
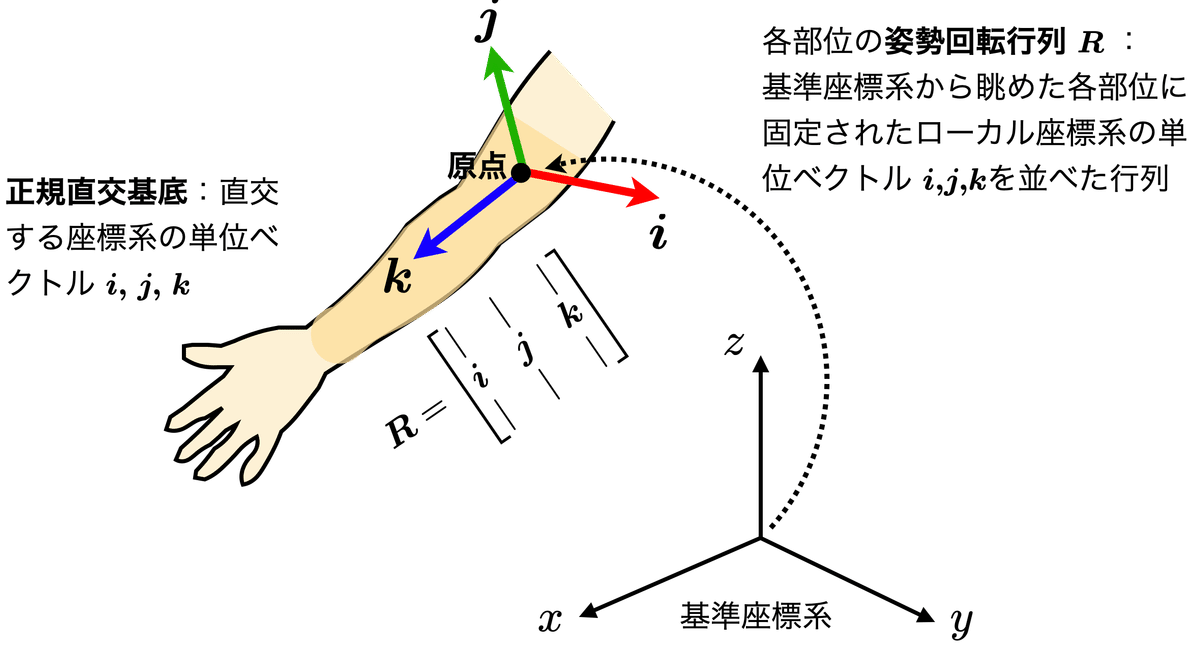
身体各部位の「座標系の定義」は,各部位の「原点」と「姿勢回転行列」から構成される.特に姿勢回転行列は「座標変換」,「解剖学的な関節角度」,そして次章で述べる「角速度」の計算で使用される(図1).
なお,各部位の座標系の原点には,Conventional Modelがこのマーカセットから推定する関節中心(補足2)を使用する.Conventional Modelの推定方法はオープンではないため,推定方法は異なると思われるが,Plug-in Gaitマーカセットからの関節中心の推定方法は文献3を参照されたい.

図2は,絶対座標系と,モーションキャプチャのモデルが規定する身体各部位に固定されたローカル座標系を示した例である.赤色(R)が$${x}$$軸,緑色(G)が$${y}$$軸,青色(B)が$${z}$$軸で定義されている.後述するように原点は部位の近位側の関節に相当する.
ただし後半に示す実際のコードでは,モーションキャプチャのOptiTrackのConventional Model(VIconのPlug-in Gait相当)のマーカセットを利用した場合の身体座標系の定義の一例を示していく.ここでは,図2とは異なり独自の姿勢回転行列を定義する.
なお,OptiTrackの場合オンラインでこれらの座標やスケルトンモデル(身体座標系情報)が得られるので,オンラインで力学計算を行うことも十分可能である.
そもそも座標系とは
バイオメカニクスでは,地球上に固定された(その意味で動かない)絶対座標系と,身体に固定されたローカル座標系に大別されるが,多くの場合,直交座標系を使用する.
図1にも示したが,直交座標系は,正規直交基底(互いに直交する大きさ1の3つの単位ベクトルを並べたもの)によって規定され,これは回転行列に相当する.また,回転行列はこれは数学的には直交行列である.なお,直交座標系はデカルト座標系,またはカーテシアン座標系とも呼ばれる(補足1).
回転行列についてはよく理解しているつもりでも,特に3次元の場合,その性質は奥深い.この直交行列の性質を正しく理解することが,回転のダイナミクスを理解するための第一歩であるから,ご興味のある方は,
なども参照していただけたらと思う.ただし力学ではこの「回転行列(直交行列)の微分」の性質の理解も重要で,それについては,第7章の角運動量の微分などの計算で一部を示してきたが,今後も少しずつになるが述べていくつもりである.
身体に固定する座標系の方向については,以下に具体的に個別に述べていくことになるが,「原点は各部位の近位側の関節に固定する」.また,他に共通するルールとして,ここでは長軸方向を$${z}$$軸としたが,このルールはとくに理由はなく正規直交基底の各軸が右手系を構成することだけ注意すれば,自由に決めていただいてよい.
直交座標系を定めるために,一般にマーカは各部位で最低3個のマーカが必要となる.ただし,以下で述べるように,解剖学的な構造を利用してその数を減らすことは関節構造の定義によっては可能である.
身体の関節は,ロボットのように綺麗な構造とはなっていないことが多く,問題設定によって大きく異なるので,ここでは,一例を示していくだけになるがご容赦いただきたい.
また,もし解剖学的な構造にこだわると関節の定義は複雑になるだろうが,ここでは単純化したモデルを採用する.
解剖学的には関節の構造は複雑で,厳密には都合よく幾何学的な定義に基づく蝶番関節や楕円関節などには収まらないことが多い.ただしこれは,座標系の定義において大きな問題点ではなく,近似的にどのように観察することが許容できるかという問題になる.
座標系の原点定義
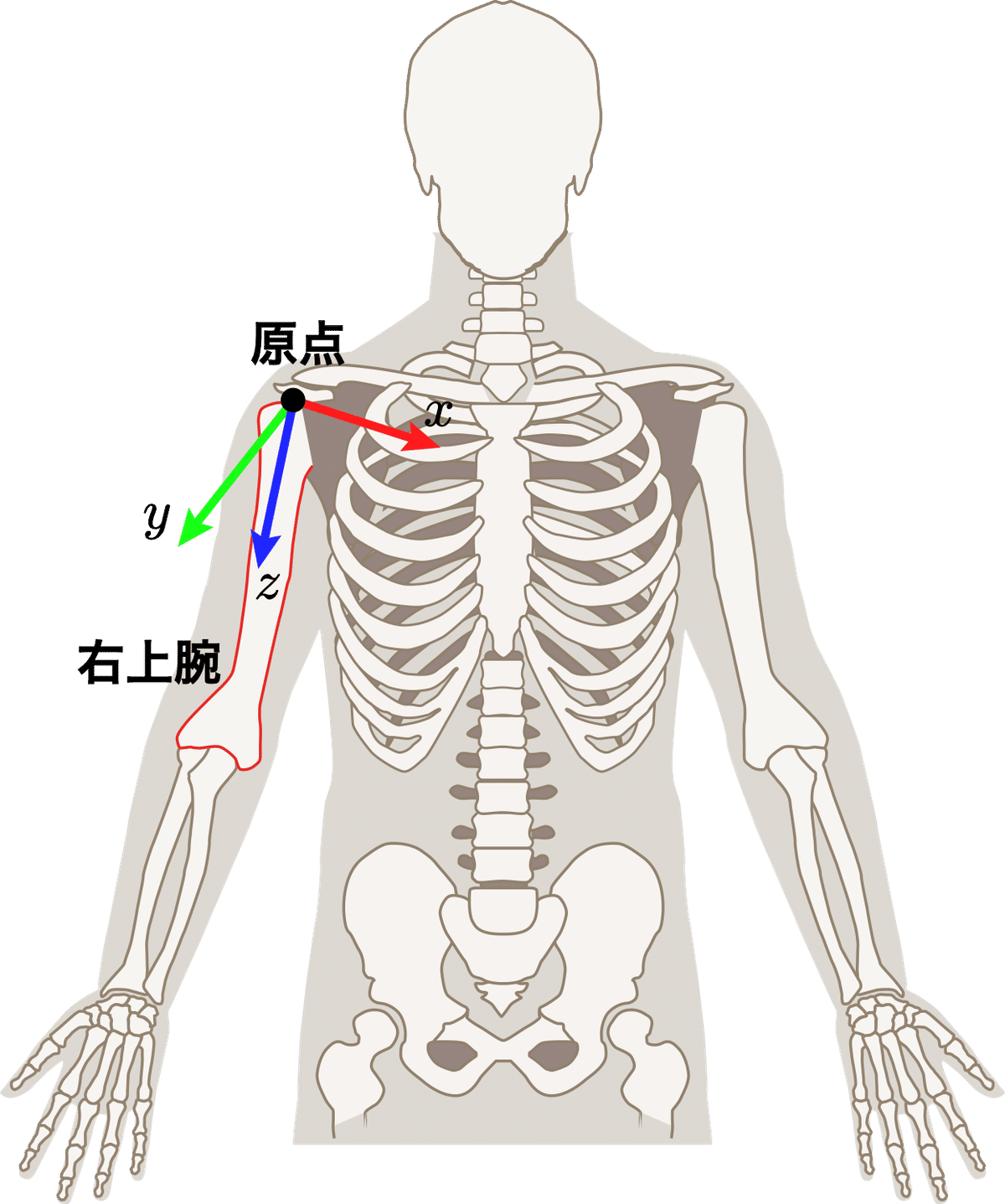
繰り返しになるが,力学計算や回転運動の記述には,身体各部位に固定された座標系の定義が必要である.座標系の「原点」は各部位の「近位側」の関節の中心とする(図3).方向は各部位での定義が必要となる.
ただし厳密に述べると,球関節と仮定できる場合を除けば,剛体運動の幾何学的な意味で,関節の軸は定義できても関節の中心は数学的には存在しない(補足2).
しかし,実用上座標系を定める上で,関節と関節を結ぶ線分を長軸と定義する必要がある.たとえば前腕の長軸方向を定めるために,手関節という点(中心)と肘関節という点(中心)を定義する必要があり,実用上,手関節と肘関節の蝶番関節を仮定し,各関節軸の内外側の両側の2つのマーカの中心を関節の基準となる点を原点と定めて良いだろう.たとえば足関節であれば,足首の内果と外果の両側にマーカを貼付しその中点を足部の座標系の原点とする.ただし,どの関節でも,厳密に解剖学的特徴点にマーカを貼付するのではなく,関節を動かして指で挟み動かない部位を探しながら軸方向を感覚的に定めるのが一般的なようだ.
ソフトウエアによっては,この関節の中心なるもの(座標系の原点)を推定する機能がある.先にも述べたがOptiTrackであれば,ViconのPlug-in gateに相当するConventional body modelがあり(図2),関節の中心(各部位の原点)座標を推定する.後述の例では,Conventional モデルが推定する原点を使用するが,モデルの推定する各部位の原点(関節の中心)の信頼度が低い場合は,前述のように関節に2つ以上のマーカーから独自に推定する必要がある.この原点を推定する数理モデルは公開されておらず,各自で精度の検証を行うしかなく,筆者も検証中である.
姿勢定義
座標系の軸は正規直交基底としての単位ベクトルであり,これを決めることは各部位の姿勢回転行列を与えることになる.また次章で述べる予定であるが,姿勢回転行列から角速度ベクトルを計算するので,この姿勢回転行列の定義は重要だ..
後ほどの計算ではConventional Modelが推定する各部位の原点を,座標系を定義するために使用するが,姿勢回転行列(座標系)は独自に定義する.各部位の座標系を定める基本は,各部位の原点間を結ぶ長軸方向とし,それを$${z}$$軸とする.長軸方向の定義は各部位の近位側の関節と遠位側の関節を結ぶ直線で定義する.
座標軸の定義は部位によって異なるが,体幹や頭部を除いた上肢や下肢では,蝶番関節を意識した軸方向の定義が中心になる.
また,手,足,頭部などの遠位端の部位には関節が存在しないので,何らかの方法で遠位端の定義が別途必要となる.
次に,上肢と下肢の座標系の定義について述べる.
上肢と下肢の座標系の定義
関節が蝶番関節構造を有するとみなしてよさそうな場合,蝶番関節をまたぐ2つの部位の各長軸($${z}$$軸)に垂直な方向を$${x}$$軸とする.そして,これらの$${z}$$軸(長軸)と,$${x}$$軸(蝶番関節軸方向)に垂直な方向を$${y}$$軸方向とする.また,上腕や大腿の$${x}$$軸も肘関節や膝関節の蝶番関節方向でを利用して定める.
しかし,たとえば肘関節でも膝関節でも,蝶番関節様の動き方をするが,前腕・上腕や下腿・大腿の各部位の長軸にその関節軸が垂直であるとは限らない.また計測上厳密には一致しない.そこで,おおよそ蝶番関節軸と一致しているはずの$${x}$$軸を定める方法として,以下の2種類の方法が考えられる.
ひとつは,原点を定めるために内外側の両側にマーカを装着する方法を述べたが,暫定的にその2つのマーカから構成される軸を利用する方法である.ただし,この軸は長軸($${z}$$軸)との直交性を保てないので,仮の軸となる.手部や足部でこの計算方法が採用される.
方法1(前腕,手):内外側のマーカを利用する方法
1:各部位の長軸($${z}$$軸)を定める.
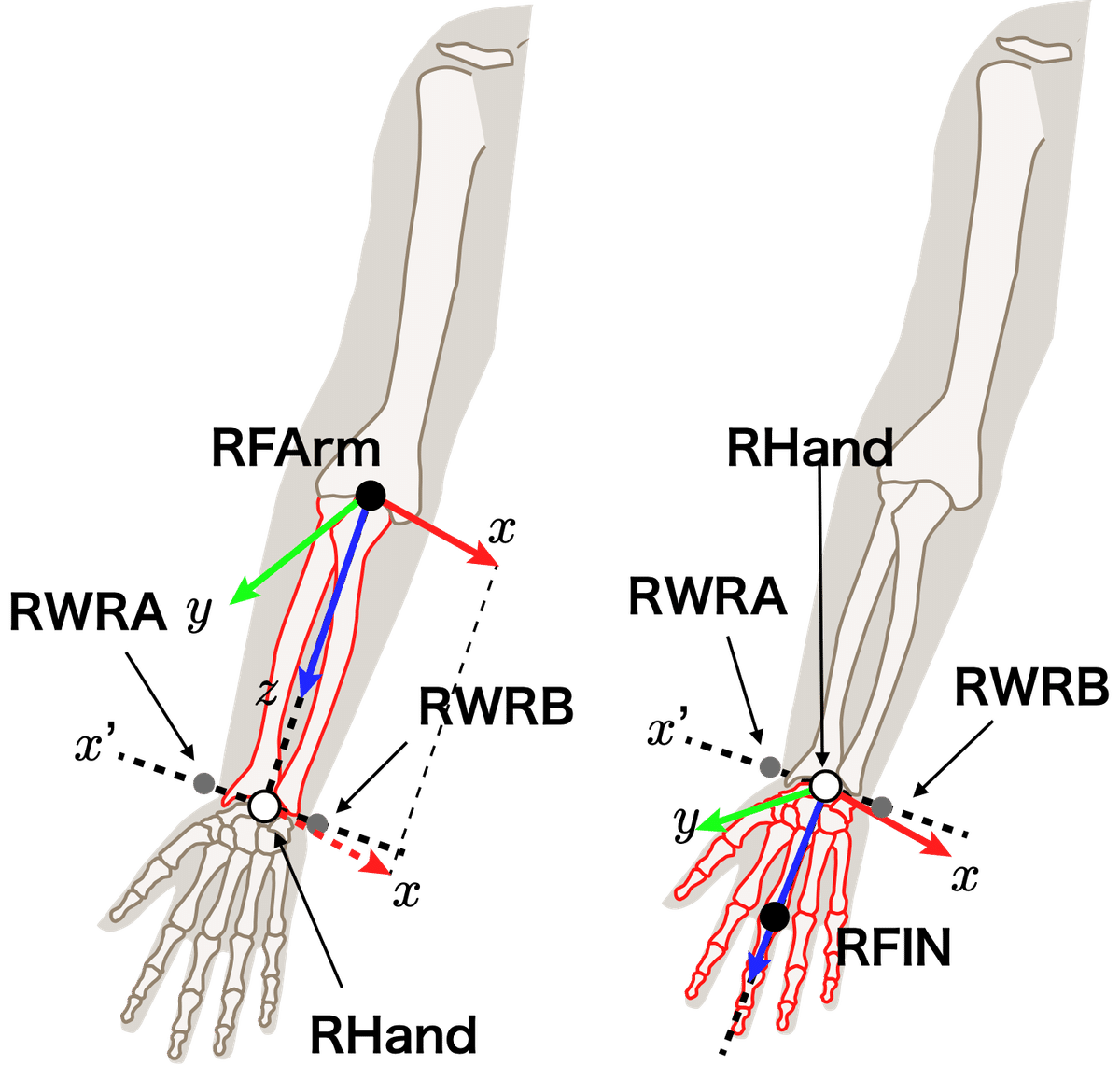
2.蝶番関節とみなす軸上の内外側の両側のマーカから構成される仮の軸方向$${x'}$$を定める(図4破線.ここでは手首の内外側の両側のマーカで定め,常に右側から左側を向くベクトルを構成.左右でマーカの内外の順番が異なるので注意).
3.ベクトルの外積などによって,$${z}$$軸と$${x'}$$軸に垂直な方向を定め,これを$${y}$$軸とする.
4.$${y}$$軸と$${z}$$軸に垂直な方向を,3と同様にベクトルの外積などによって定め,これを最終的な$${x}$$軸とする.
図4に示したように,長軸周りの回内外運動は前腕の運動と仮定し,回内外運動を同定するために手首の2つのマーカを利用する.したがって,前腕と手の$${x}$$軸は共通となる.
関節の両側にマーカを装着できない場合は,次の方法2が考えれる.
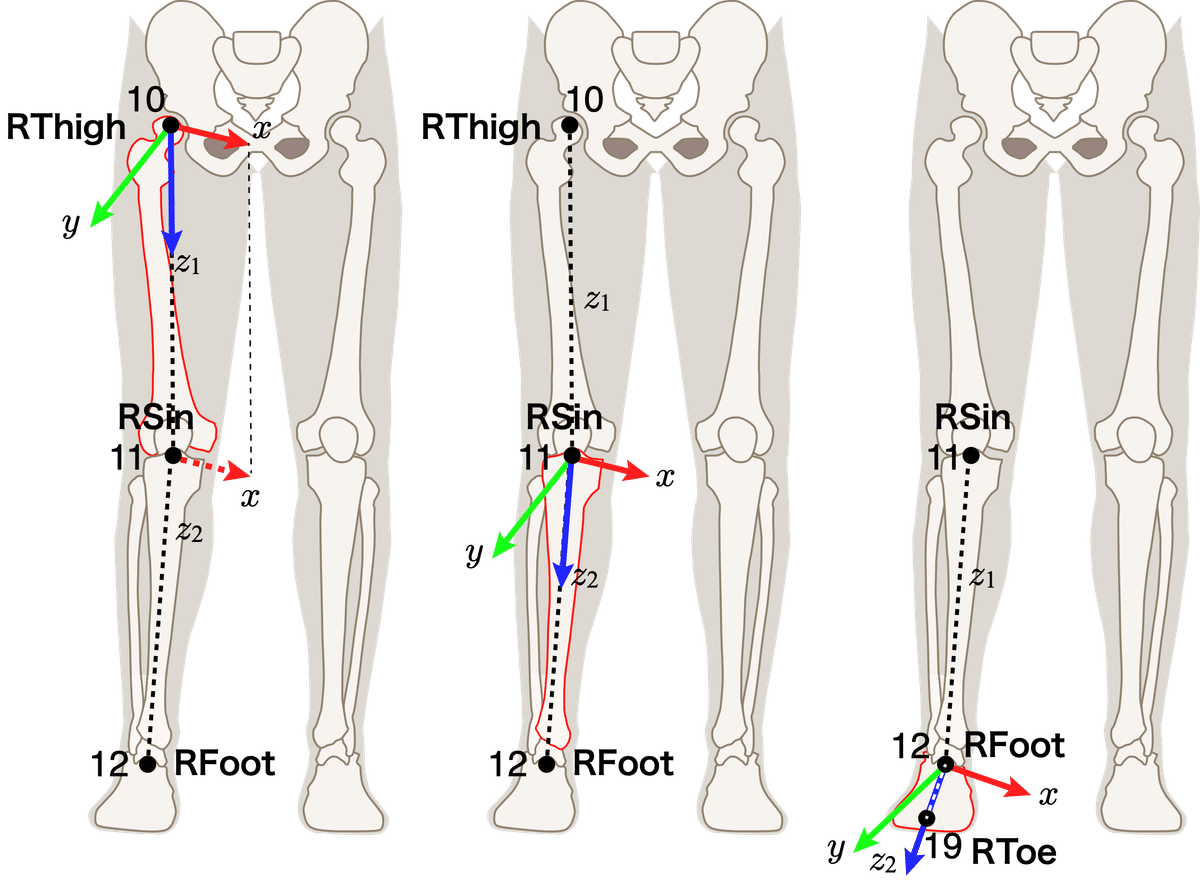
方法2(上腕,大腿,下腿,足):2つの部位の長軸に対する直交軸の利用
1.該当する部位の長軸($${z}$$軸)と,隣の部位(近位側,遠位側の両方の可能性がある長軸($${z_{\pm}}$$軸)も定める.
2.$${z}$$軸と$${z_{\pm}}$$軸に垂直な軸方向を$${x}$$軸とする.
3.長軸($${z}$$軸)と,$${x}$$軸に垂直な軸を,ベクトルの外積などによって定め,$${y}$$軸とする.
基本的に,座標軸を定めるために必要なマーカまたは位置情報は,は3つの部位の原点(関節中心)で,各部位の長軸の情報が与えられれば良い.
被験者によっては,関節の可動域が180度を超えて,肘や膝関節で過伸展となるかもしれないが,このコードではその対応はできていないので注意されたい.また180度近くになると角度精度が劣化する問題もある.
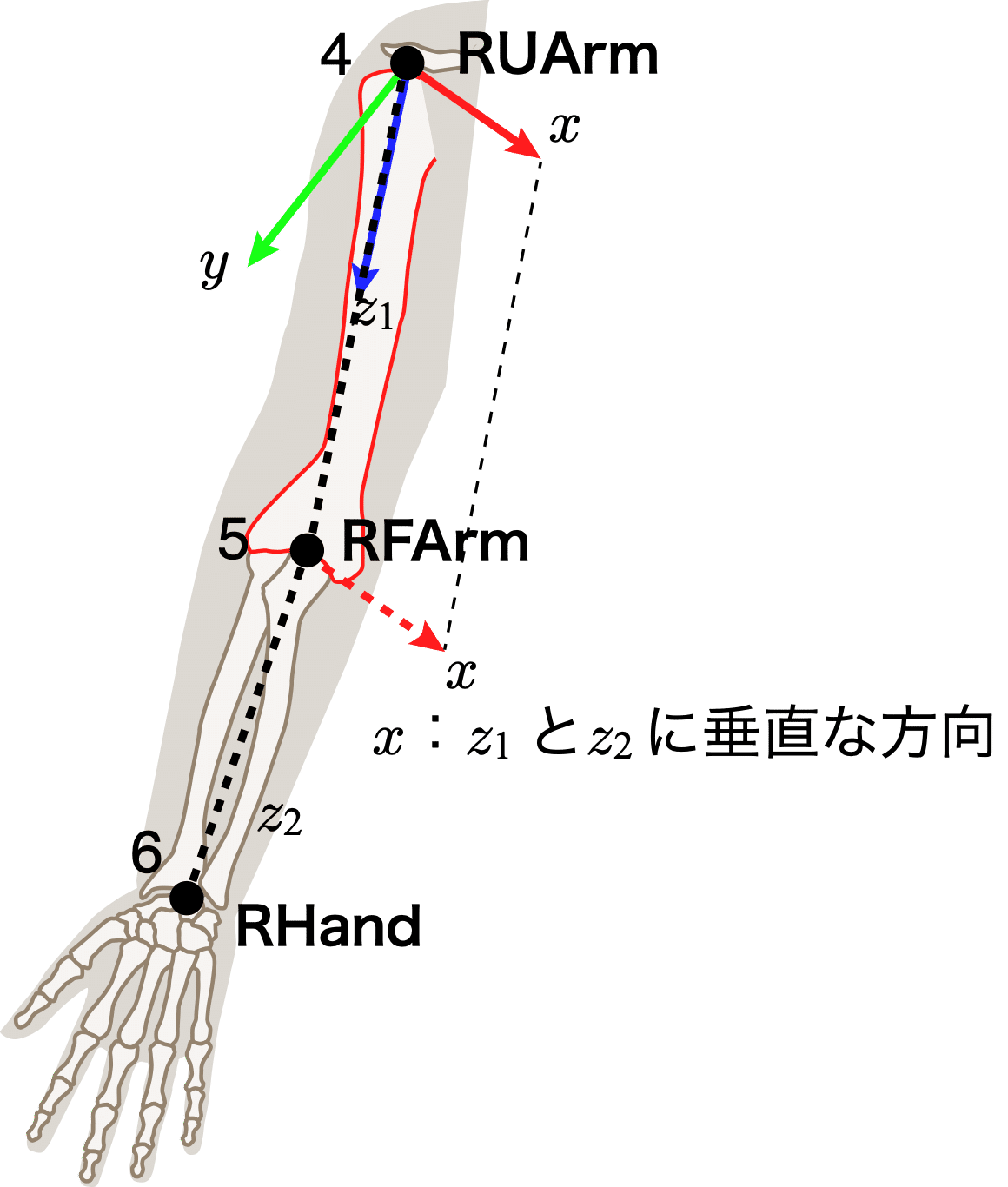
方針1は一見良さそうな方法だが,マーカーの貼付位置の誤差に依存する.方針2は,蝶番関節軸である$${x}$$軸を正確に定める意味で合理的な方法であるが,伸展位近くでどの程度誤差が発生するかの検証が必要かもしれない.
なお,方法1,2はあくまでも軸の定義で,軸の正負の定義はユーザの定義に委ねる.ここでは,計算過程での混乱を避けるため,左右も含めて全ての関節で,図4,5,6の姿勢において,常に$${y}$$軸が前方向きになるような$${x}$$軸の方向,すなわち左方向を向く方向を$${x}$$軸の正とした.解剖学的な定義に従い,伸展・屈強などで統一的な方向にしてもよいだろう.
図4,5に前腕の例を示したが,ここでは上腕もこの肘関節(前腕)の$${x}$$軸と同じ軸を利用している.また,下肢の大腿,下腿,足についても同様である(図6).
さて,手や足などのように実際の関節は楕円関節や顆状関節であったり,これらの関節に限らず,多くの関節は厳密に述べればきれいな幾何学的な関節構造ではなく,可動域の拘束や幾何学的な拘束付きの並進3+回転3の6自由度の関節である.各関節はこのように異なる軸回転を構造上許すが,ここでは座標系の定義を行うために,蝶番関節に相当する軸方向を定めることを優先している.
体幹・頭部の座標系の定義
これらの部位も,前述の方針1に基づいた方法で定義する.
動かして学ぶ姿勢回転行列の計算
これまでのコードに,姿勢回転行列の計算を行う関数を加筆し,新たに加えたその行列のインスタンス変数rotに各部位の姿勢回転行列を代入する.
この回転行列は,ここでは大きく分けて2種類の方法しか定義方法はないが,マーカや身体の定義次第で,すなわち人によって大きく異なるだろう.その意味で,柔軟に定義を変えていけば良い.
なお,コードは,これまで同様に,以下のGoogle Colaboratoryのリンクから,ブラウザでPythonコードを実行できるようにした.なお,ログインするためには,Googleアカウントが必要となるので注意をされたい.
また,使用するモーションキャプチャのサンプルデータ(sample_optitrack_221027.csv)とフォースプレートのサンプルデータ(sample_fp_221027.csv)は,このリンクからダウンロードして,Google Driveをマウントし,マウントしたドライブにそれらをコピーしてご使用いただきたい.これは,第6章で使用したデータと同じであるので,すでにダウンロ度済みの方は,サイドダウンロードする必要はない.
パッケージの読み込み
Pandas(データの読み込み),Numpy(行列演算),matplotlib(グラフ)等のパッケージの読み込みを行う.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#from scipy.interpolate import interp1d
import copy
from scipy.interpolate import UnivariateSplineデータをダウンロードして,ユーザのファイルの置き場所にあわせて以下を変更する.
from google.colab import drive
drive.mount('/content/drive')以下は各自の環境にあわせて設定していただきたい.前述のように,すでにダウンロード済みの方は,同じファイルを使用されたい.
file_path_op_9 = '/content/drive/MyDrive/.../sample_optitrack_221027.csv'class BodyLinkの定義(逆動力学計算の本体)
各部位(link)の原点を構成する位置ベクトルのタイプ(Bone, Bone Marker, Marker)を加筆した.これはOptiTrack特有のcsvファイルの出力に依存している.
# new9:追記・変更箇所
class BodyLink:
def __init__(self, l_id:int, name:str, m_type:str, mass_ratio:float, cg_ratio:float):
self.l_id = l_id # linkのID
self.name = name # linkの名前
self.m_type = m_type # マーカの種類(Bone, Bone Marker, Marker)(new9)
self.mass_ratio = mass_ratio # linkの質量分配比
self.cg_ratio = cg_ratio # linkの重心位置の分配比 (new6)
self.inertia_moment = None # linkの慣性モーメント (new8)
self.child_val = None # 子供の変数
self.sister_val = None # 兄弟姉妹の変数
self.distal_val = None # linkの遠位端の変数 (new6)
self.p = None # linkの関節の原点(近位端) (new8)
self.cg = None # linkの重心位置
self.acc = None # linkの重心の加速度
self.force = None # linkの関節に作用する力
self.rot = None # linkの姿勢行列 (new9)
# BodyLinkを一旦作成してから,その後に親子,兄弟姉妹関係をBodyLinkに与える.
def set_child_sister(self, child_val, sister_val):
self.child_val= child_val
self.sister_val = sister_val
# (new6)
# リンク(部位)の重心を計算するためには,リンクの原点(近位端)と遠位端の位置ベクトルが必要
# ただし,末端のリンク(部位)には子供のリンク(部位)がないので,リンクの遠位端(関節)の情報を得られない
# BodyLinkを一旦作成してから,その後に,各リンクの遠位端の位置をBodyLinkに与える.親子関係とは区別して利用
def set_distal_end(self, distal_val): # (new6)
self.distal_val= distal_val
# m * (acc - g)
def CgForce(self, bw):
gravity = [0., 0., -9.8] # 重力加速度ベクトル
return bw * self.mass_ratio * (self.acc - gravity)
# Inverse Dynamics Newton equation(改訂)
def ID_Newton(self, bw, sister=False, fp=True):
if self.name == 'RToe': # (new6)右足の場合,床反力2を返す
return self.force
elif self.name == 'LToe': # (new6)左足の場合,床反力1を返す
return self.force
elif self.l_id == 0:
return 0.0
elif sister == False: # 部分(そこから遠位:子供のみ)の解析
f = self.CgForce(bw)+\
self.child_val.ID_Newton(bw, sister)
self.force = f
return f
elif sister == True: # 全身解析(兄弟姉妹を含む)
f = self.CgForce(bw)+\
self.child_val.ID_Newton(bw, sister)+\
self.sister_val.ID_Newton(bw, sister)
self.force = f
return f
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# 合成の質量(全質量)の計算
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
# bw: 体重
def Resultant_Mass(self, bw, sister=False):
if self.l_id == 0:
return 0.0
elif sister == False: # 部分(そこから遠位のみの)解析
return bw * self.mass_ratio + (self.child_val).Resultant_Mass(bw, sister)
elif sister == True: # 全身解析
return (bw * self.mass_ratio +(self.child_val).Resultant_Mass(bw, sister) +
(self.sister_val).Resultant_Mass(bw, sister))
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# m * cg
def WeightedJoint(self, bw):
return bw * self.mass_ratio * self.cg
# 合成の(全)WeightedJoint
# Σ m_i * cg_i
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
def Resultant_WeightedJoint(self, bw, sister=False):
if self.l_id == 0:
return 0.0
elif sister == False: # 部分(そこから遠位のみの)解析
return self.WeightedJoint(bw)+\
(self.child_val).Resultant_WeightedJoint(bw, sister) #, sister)
elif sister == True: # 全身解析
return self.WeightedJoint(bw)+\
self.child_val.Resultant_WeightedJoint(bw, sister)+\
self.sister_val.Resultant_WeightedJoint(bw, sister)
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# 合成重心
# Resultant_WeightedJoint() / Resultant_Mass()
# = Σ(m_i * cg_i) / Σ m_i
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
def Resultant_Cg(self, bw, sister=False):
return self.Resultant_WeightedJoint(bw, sister)/self.Resultant_Mass(bw, sister)
b_link = [0] * 27 # 配列の初期化
b_link[0] = BodyLink(0, '', '', .0, .0) # 0のときストップ
b_link[1] = BodyLink(1, 'Hip', 'Bone', .187, (1.-.609)) # 腰(下体幹)
b_link[2] = BodyLink(2, 'Chest', 'Bone', .302, (1.-.428)) # 胸(上体幹)
b_link[3] = BodyLink(3, 'Neck', 'Bone', .069, (1.-.821)) # 頭部
b_link[4] = BodyLink(4, 'RUArm', 'Bone', .027, .529) # 右上腕
b_link[5] = BodyLink(5, 'RFArm', 'Bone', .016, .415) # 右前腕
b_link[6] = BodyLink(6, 'RHand', 'Bone', .006, .891) # 右手
b_link[7] = BodyLink(7, 'LUArm', 'Bone', .027, .529) # 左上腕
b_link[8] = BodyLink(8, 'LFArm', 'Bone', .016, .415) # 左前腕
b_link[9] = BodyLink(9, 'LHand', 'Bone', .006, .891) # 左手
b_link[10] = BodyLink(10, 'RThigh', 'Bone', .110, .475) # 右大腿
b_link[11] = BodyLink(11, 'RShin', 'Bone', .051, .406) # 右下腿
b_link[12] = BodyLink(12, 'RFoot', 'Bone', .011, (1.-.595)) # 右足
b_link[13] = BodyLink(13, 'LThigh', 'Bone', .110, .475) # 左大腿
b_link[14] = BodyLink(14, 'LShin', 'Bone', .051, .406) # 左下腿
b_link[15] = BodyLink(15, 'LFoot', 'Bone', .011, (1.-.595)) # 左足
# 各リンクの遠位端も定義(遠位端の位置ベクトルを計算するためだけに必要な変数 (new6)
b_link[16] = BodyLink(16, 'Head', 'Bone', .0, .0) # 3 Neckの遠位端
b_link[17] = BodyLink(17, 'RFIN', 'Bone Marker',.0, .0) # 6 RHandの遠位端
b_link[18] = BodyLink(18, 'LFIN', 'Bone Marker', .0, .0) # 9 LHandの遠位端
b_link[19] = BodyLink(19, 'RToe', 'Bone', .0, .0) # 12 RFootの遠位端
b_link[20] = BodyLink(20, 'LToe', 'Bone', .0, .0) # 15 LFootの遠位端
# 手,前腕の姿勢回転行列を計算するためだけに必要な変数 (new9)
b_link[21] = BodyLink(21, 'RWRA', 'Bone Marker', .0, .0) # 右手首橈骨側
b_link[22] = BodyLink(22, 'RWRB', 'Bone Marker', .0, .0) # 右手首尺骨側
b_link[23] = BodyLink(23, 'LWRA', 'Bone Marker', .0, .0) # 左手首橈骨側
b_link[24] = BodyLink(24, 'LWRB', 'Bone Marker', .0, .0) # 左手首尺骨側
b_link[25] = BodyLink(25, 'RFHD', 'Bone Marker', .0, .0) # 右前頭
b_link[26] = BodyLink(26, 'LFHD', 'Bone Marker', .0, .0) # 左前頭motion capture の csv file から情報を抽出する関数
以下は,motion captureのデータからマーカの位置ベクトルを抽出する関数.
m_typeの追加に伴い,extra_marker()を修正した.
# CSVデータからヘッダだけ抽出
def extract_df_header(file_path):
return pd.read_csv(file_path, header=None, nrows=5, index_col=1).T
# skeletonの名前を抽出
def extract_skeleton_name(file_path):
df = extract_df_header(file_path)
marker_name = df['Name'][2]
position_col = marker_name.find(':')
return marker_name[:position_col]
# ファイル名,マーカ名,マーカタイプを引数に与えて各Linkの重心の加速度データを抽出する関数 (new9)
# marker_typeとして,'Bone'(default), 'Bone Marker, 'Marker' を選択できるように修正 (new9)
def extract_marker(file_path, marker_name, marker_type='Bone'):
sk_name = extract_skeleton_name(file_path) # skeleton
df_main = pd.read_csv(file_path, header=[4]) # データだけ抽出
df = extract_df_header(file_path) # headerだけ抽出
df_selected = df[(df['Type']==marker_type) & (df['Name']== sk_name+':'+marker_name)] # ヘッダがNameとTypeの両方が一致する部分だけ抽出
selected_rows = df_selected.index # 一致する列
marker_data = np.array(df_main.iloc[:, selected_rows[-3:]].values) # 後ろから3個データを取得す
return marker_data[:, [2,0,1]] # OptiTrackの座標がYup(Y軸が上)のため,座標を入れ替えることで,Zupに変更する数学関数
以下は,ノルム(ベクトルの大きさ)や単位ベクトルを計算する関数定義.
# (new8)
# ノルム(大きさ)
def norm(vec_array):
return np.linalg.norm(vec_array, axis=1)
# (new9)
# 単位ベクトル
def unit_vec(data_vec):
data_norm = np.linalg.norm(data_vec, axis=1)[:,np.newaxis]
return data_vec/data_normスプライン平滑化
第6章で述べたスプライン平滑化関数.
インスタンス変数pにマーカの位置ベクトルなどを格納する際,これを使用し平滑化してから格納する.これまでは,CSVデータのまま格納していたが,変更した.
# (new6)
# 微分と平滑化を同時にスプライン平滑化で行う
# order=0:変位(微分を行わない),order=1:速度, order=2:加速度
def smoothing_spline(vec_data, weight, sf, order=0, degree=4):
vec_copy = copy.copy(vec_data)
vec_data_t = vec_copy.T
len_num = len(vec_data)
len_vec = len(vec_data_t)
time = np.arange(0, len_num) / sf
w_a = [np.isnan(x) for x in vec_data_t]
spl = [0]*len_vec
for i in range(len_vec):
vec_data_t[i][w_a[i]] = 0.
w_a[i] = ~w_a[i]
spl[i] = UnivariateSpline(time, vec_data_t[i], w_a[i], s=weight, k=degree).derivative(n=order)(time)
return np.array(spl).T親子関係(child_val),兄弟姉妹関係(sister_val),遠位端(distal_val)の情報をクラスb_linkに格納
以下は,以前の定義と同様である.
# 親子関係と兄弟姉妹関係を下記でb_linkのchild_val, sister_valに追記
child_sister_list = [
[1,2,0], [2,3,10], [3,0,4], [4,5,7], [5,6,0], [6,0,0], [7,8,0],
[8,9,0], [9,0,0], [10,11,13], [11,12,0], [12,0,0], [13,14,0],
[14,15,0], [15,0,0]]
[b_link[i[0]].set_child_sister(b_link[i[1]], b_link[i[2]]) for i in child_sister_list];
# 各リンクの遠位端の情報を格納.b_linkのcdistal_valに追記 (new6)
distal_end_list = [
[1,2], [2,3], [3,16], [4,5], [5,6], [6,17], [7,8],
[8,9], [9,18], [10,11], [11,12], [12,19], [13,14],
[14,15], [15,20]][b_link[i[0]].set_distal_end(b_link[i[1]]) for i in distal_end_list];各リンクの原点(p)の格納(修正・加筆)
各部位の位置ベクトルをCSVファイルから読み込む.
部位の原点に相当するマーカの名前とマーカのタイプを,クラスで指定する(この章から,マーカのタイプを新たに指定しているように変更したので注意されたい).
# 修正(new9)
# リンクの原点の位置ベクトル
def joint_vec(b_link, l_id, path):
if l_id == 0:
return .0
else:
joint_name = b_link[l_id].name
joint_type = b_link[l_id].m_type
return extract_marker(path, joint_name, joint_type) この章から,位置ベクトルにも,速度や加速度ベクトルの計算と数学的な整合性を持たせるために,平滑化スプラインでフィルタリングを行うこととした.
# (new9)
# 関節位置をBodyLinkクラスに格納
# 部位を指定し,関節位置ベクトルを計算し,BodyLinkのpに格納する関数
def set_link_p_list(b_link, l_id_list, path, weight = .00001, sf = 360.):
for n in l_id_list:
b_link[n].p = smoothing_spline(joint_vec(b_link, n, path), weight, sf, order=0)
以下は,各部位の原点ではなく,手,前腕等の姿勢回転行列を計算するために必要な,補助的に必要なマーカ(たとえば手首の両側のマーカ)の位置ベクトルをクラスのpに格納するための関数.
# (new9)
# 手と前腕の姿勢回転行列を計算する際に,補助的に必要な手首の両側のマーカRWRA, RWRB, LWRA, LWRBをBodyLinkクラスに格納
def set_rot_p_list(b_link, l_id_list, path, weight = .00001, sf = 360.):
for n in l_id_list:
joint_name = b_link[n].name
joint_type = b_link[n].m_type
marker_vec = extract_marker(path, joint_name, joint_type)
b_link[n].p = smoothing_spline(marker_vec, weight, sf, order=0)以下で,l_idの1~20まで格納し,21~26は姿勢回転行列を計算するために必要な補助的なマーカの位置ベクトルを格納する.
# 関節位置をBodyLinkのpに格納
set_link_p_list(b_link, range(1,21), file_path_op_9)
# 姿勢回転行列を計算するために必要なマーカ位置ををBodyLinkのl_id: 21~24のpに格納
set_rot_p_list(b_link, range(21,27), file_path_op_9)姿勢回転行列(座標軸 rot)の定義・格納
以下の関数で各リンクの姿勢回転行列(座標軸)を計算,格納する.リンクによって計算方法が異なり,計算方法のmethod1, method2の割当もここの記述した.
# (new9)
# bodylinkと部位のl_idを指定し,各linkの姿勢行列を計算し,インスタンスrotに格納
def set_frame(b_link, l_id, frame_dict):
method1 = [1, 2, 3, 5, 6, 8, 9]
method2 = [4, 7, 10, 11, 12, 13, 14, 15]
f_dict = frame_dict[l_id]
if any(l_id == elem for elem in method1):
b_link[l_id].rot = frame_method1(f_dict[0], f_dict[1], f_dict[2], f_dict[3])
elif any(l_id == elem for elem in method2):
b_link[l_id].rot = frame_method2(f_dict[0], f_dict[1], f_dict[2], l_id)
else:
print('error')
def set_frame_link(b_link, l_id_list, frame_dict):
for n in l_id_list:
set_frame(b_link, n, frame_dict)部位で姿勢回転行列の計算方法が異なる(2種類).
# (new9)
# 2つの位置ベクトルの差分(distal - origin)
# origin, headの順番で指定
def diff_joint_vec(j_origin_id, j_head_id):
return b_link[j_head_id].p - b_link[j_origin_id].p
# 手,前腕の座標系
# 手首の外・橈骨側マーカA,内・尺骨側マーカB を利用
# 左右で以下のマーカの順番が異なるので注意.右はRWRA, RWRBの順で指定.左はLWRB, LWRAの順で指定
# x軸:蝶番関節方向
# z:長軸,y:前後方向
# z軸は近位から遠位方向なので,右は回外,左は回内に相当
def frame_method1(j_origin_id, j_head_id, j_right_id, j_left_id):
joint_unit_axis_z = unit_vec(diff_joint_vec(j_origin_id, j_head_id))
joint_axis_x = diff_joint_vec(j_right_id, j_left_id)
joint_unit_axis_y = unit_vec(np.cross(joint_unit_axis_z, joint_axis_x))
joint_unit_axis_x = np.cross(joint_unit_axis_y, joint_unit_axis_z)
return np.array([joint_unit_axis_x, joint_unit_axis_y, joint_unit_axis_z])
# 上腕,大腿,下腿,足の座標系
# 3つの関節中心座標が計算に必要
# x軸:蝶番関節方向(伸展屈曲軸)
# z:長軸,y:前後方向
def frame_method2(j1_list, j2_list, j3_list, joint_id=4):
joint_unit_axis_z1 = unit_vec(diff_joint_vec(j1_list, j2_list)) # z1: joint1 → joint2
joint_unit_axis_z2 = unit_vec(diff_joint_vec(j2_list, j3_list)) # z2: joint2 → joint3
# 関節の構造と外積の性質から,部位によって左右軸のx軸の向きが変化する(注意:過伸展に未対応)
lst1 =[4, 7, 12, 15]
lst2 =[10, 13, 11, 14]
if any(joint_id == elem for elem in lst1):
pm = -1.
elif any(joint_id == elem for elem in lst2):
pm = 1.
joint_unit_axis_x = pm * unit_vec(np.cross(joint_unit_axis_z1, joint_unit_axis_z2))
lst3 =[4, 7, 10, 13]
lst4 =[11, 14, 12, 15]
if any(joint_id == elem for elem in lst3):
joint_unit_axis_y = np.cross(joint_unit_axis_z1, joint_unit_axis_x) # y1軸
return np.array([joint_unit_axis_x, joint_unit_axis_y, joint_unit_axis_z1])
elif any(joint_id == elem for elem in lst4):
joint_unit_axis_y = np.cross(joint_unit_axis_z2, joint_unit_axis_x) # y2軸
return np.array([joint_unit_axis_x, joint_unit_axis_y, joint_unit_axis_z2])以下の辞書に,座標軸の計算方法に必要なマーカの情報を格納する.
# (new9)
# 各リンクの座標軸を計算するための辞書情報
# [linkのID, [軸計算方法の種類, [マーカ名1, マーカ1のタイプ],[マーカ名2, マーカ2のタイプ],[]]]
# 順番に注意
frame_dict = dict([
[1, [1, 2, 10, 13]], # 腰(下体幹) method1
[2, [2, 3, 4, 7]], # 胸(上体幹) method1
[3, [3, 16, 25, 26]], # 頭 method1
[4, [4, 5, 6]], # 右上腕 method2
[5, [5, 6, 21, 22]], # 右前腕 method1
[6, [6, 17, 21, 22]], # 右手 method1
[7, [7, 8, 9]], # 左上腕 method2
[8, [8, 9, 24, 23]], # 左前腕 method1
[9, [9, 18, 24, 23]], # 左手 method1 (順番に注意)
[10, [10, 11, 12]], # 右大腿 method2
[11, [10, 11, 12]], # 右下腿 method2
[12, [11, 12, 19]], # 右足 method2
[13, [13, 14, 15]], # 左大腿 method2
[14, [13, 14, 15]], # 左下腿 method2
[15, [14, 15, 20]] # 左足 method2
])最終的に,以下の計算で各部位の姿勢回転行列(rot)をb_linkに格納する.
set_frame_link(b_link, range(1,16), frame_dict)例(腰)
b_link[1].rot
>>>
array([[[ 0.998149 , -0.0540189 , 0.02793817],
[ 0.99815342, -0.05395653, 0.02790062],
[ 0.99815686, -0.05390468, 0.02787777],
...,
[ 0.96157407, 0.26911967, 0.05431308],
[ 0.96162632, 0.26889361, 0.0545073 ],
[ 0.96167757, 0.26866926, 0.05470905]],
[[ 0.05582513, 0.99608671, -0.06851877],
[ 0.05575591, 0.99610296, -0.06833868],
[ 0.05569802, 0.99611909, -0.0681505 ],
...,
[-0.27453821, 0.94400014, 0.18300956],
[-0.27435345, 0.94404668, 0.18304659],
[-0.27417191, 0.94408571, 0.18311725]],
[[-0.02412753, 0.0699516 , 0.99725856],
[-0.02410457, 0.06976811, 0.99727197],
[-0.02409595, 0.06957763, 0.99728549],
...,
[-0.00202009, -0.19088826, 0.98160969],
[-0.00223738, -0.19097668, 0.98159202],
[-0.00245206, -0.19109944, 0.98156762]]])ここでは,姿勢回転行列を構成する3つの基底ベクトルを3次元配列として表していることに注意されたい.上記の例だと,
[[ 0.998149 , -0.0540189 , 0.02793817],
[ 0.05582513, 0.99608671, -0.06851877],
[-0.02412753, 0.0699516 , 0.99725856]]が最初のフレームの回転行列に相当する.
次章の予定
次章
では,この姿勢回転行列rotを利用して,身体各部位の角速度ベクトルを計算する.
補足
補足1:Descartes座標系
直交座標系はデカルトが座標系の概念を考えだしたことに由来する.デカルトの綴はDescartesだが,分解するとdes Cartesとなっており,desがofの意味で,Cartesian座標系とも呼ぶ(たしか英語ではデカルトとは呼ばず,Cartesianと呼ぶと学生のときに習った記憶があるが,定かではない...辞書を見ていると英語でもDescartesと使用しているようだ.ネイティブと話す機会があれば確認しておく).
補足2:関節中心
身体各部位の座標系は原点と座標軸の方向で定まる.原点は関節中心なるもので定めれば良いと考えるだろう.膝関節であれば,大腿骨内側顆と外側顆あたりで,膝関節の伸展運動を行っても動かない両側の点にマーカを貼付し,その中点を関節の原点として定めることが一般的である.実際それで実用上十分である.
ただしここでは,関節の中心なるものを数学的に定義することを試みる.「剛体」の運動は並進と回転運動で構成されるが,それは座標系の選択の仕方によって並進と回転の割合が異なってしまう.ただし,座標系を適切に選択すれば,一つの回転でだけで記述できる回転軸が唯一存在する.このような一つの回転だけで剛体の運動を記述できる軸を瞬間回転軸(screw axis,helical axis)と呼ぶ.これは3次元空間で剛体の角速度ベクトルと,剛体の任意の点の速度ベクトルがあれば,3次元空間において軸として厳密に計算できる(補足3).
この考え方を利用すれば,大腿と下腿の2つの座標系から見た剛体(たとえば大腿)の瞬間回転軸を定義することは計算できる.しかし,それはあくまでも「軸」であって「点」ではない.瞬間回転軸はあくまでも軸を定めるだけである.これが数学的に「関節中心」なるものの定義が困難な理由である.結論からすると数学的には(関節の)中心は存在しない.そこで回転軸の集合から,どのように定義するかは,学会や研究者自身で定義されるものと考えるべきだろうが,その議論が数学的・幾何学的な背景をもとにしっかりとおこなわれているかは筆者の知る範囲ではわからない(勉強不足という意味も込めて).
「関節中心」なるものの定義が困難な理由のもう一つは,解剖学的にも関節構造が複雑で,ゆらぎや誤差ではなく関節軸すら一定ではないということもある.
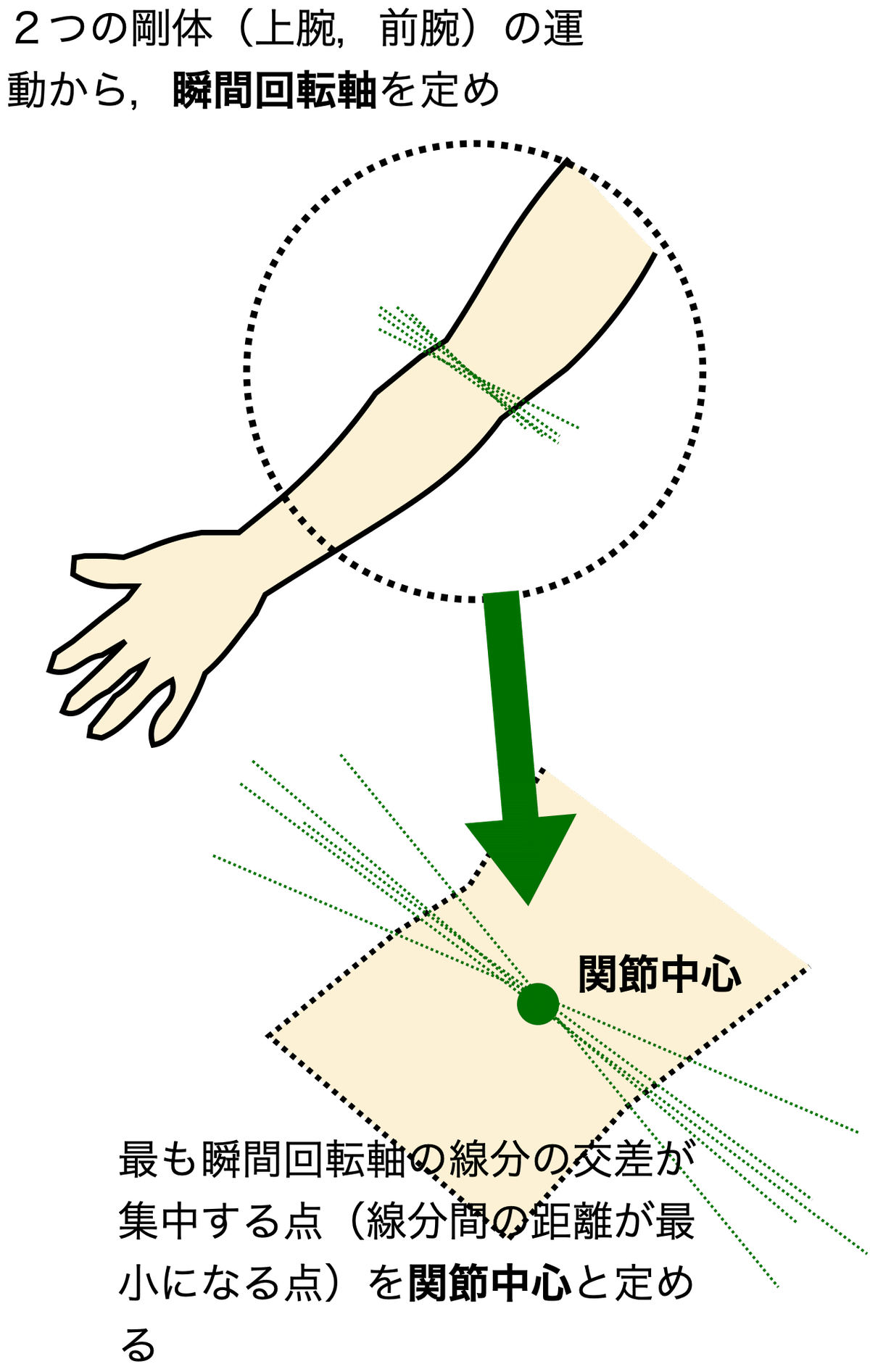
しかし,もし,関節構造が球関節,楕円関節,顆状関節などであるば,剛体の瞬間回転軸はいろいろな方向を向くことが可能で,その軸を構成する線分が集中する点が存在するだろう.厳密にはそれらの線分は交差しないので,最もその線が集中する位置(各線分間の距離が最小となる点)を,関節中心として定めることは可能である(図7).ただし,関節の形状によっては瞬間回転軸が平行移動するだけで,軸は計算できても計算が行いにくい(収束しにくい)形状もあるかもしれない.
なお,これはモーションキャプチャの座標位置の定め方と同じである(モーキャップではRayが最も集中する点として定義される).
の図7も参照.
また,実際に計測してみないとわかないが,膝関節の瞬間回転軸を観察すると,平行移動するだけで,線分が集中する点が存在しないかもしれない.ご自身で確認してみるとよいだろう.
なお,この瞬間回転軸を通して観察する関節軸は,絶対座標形から見た剛体(下腿などの部位)の瞬間回転軸ではなく,関節を構成する(たとえば膝関節)もうひとつの部位(たとえば大腿)に固定された座標系から見た瞬間回転軸である必要があるので注意されたい.
機会があれば,どこかで関節中心についても述べていきたい.
なお,蛇足になるが,関節構造が複雑で幾何学的に関節軸は一定ではないことを考えると,厳密には,各部位(セグメント)の長さも一定ではなく可変,または関節軸を一定としない数理モデルなど,どこかで辻褄を合わせる必要がある.議論の余地は大いにあるが,筆者は部位の長さを可変長としてつじつま合わせをするのが,合理的ではないかと考えている.
補足3:瞬間回転軸の計算
剛体がある点$${\text{o}}$$まわりに角速度$${\bm{\omega}}$$で回転しているとする.すると,点$${\text{o}}$$からみた剛体上の任意点$${\text{P}}$$の位置ベクトルを$${\bm{r}}$$とすると,ベクトル方程式
$$
\dot{\bm{r}} = \bm{\omega} \times \bm{r}
$$
で記述できる.一般に,ベクトルの積は内積(スカラ積)と外積(ベクトル積)が成り立つが,それらの除算は成り立たない.したがって,この式から$${\bm{\omega}}$$による除算によって$${\bm{r}}$$を求めようなどと考えてはいけない(学生のころ,角速度ベクトルを算出するために外積をスカラの乗算のように扱い除算を行った学術論文を見かけた.少々呆れ返ることだが査読が機能しておらず衝撃的な論文であった).
ただし,これを満たす$${\bm{r}}$$は,ある特別な場合にだけ存在し,このベクトル方程式の除算が成立する.その必要十分条件は
$$
\bm{\omega}^T \dot{\bm{r}} = 0
$$
が成り立つときで,そのとき解は
$$
\bm{r} = \frac{\dot{\bm{r}} \times \bm{\omega}}{||\bm{\omega}||^2} + c \bm{\omega}
$$
である.ここで$${c}$$は任意の定数で,$${\frac{\dot{\bm{r}} \times \bm{\omega}}{\bm{\omega}^2}}$$の位置から,ベクトル$${\bm{\omega}}$$の方向であれば,任意の位置で構わないことを示している.これを外積におけるベクトルの除法と呼び,必要十分条件を満たす任意のベクトルに対して成り立つ(補足4)(文献4).
ただし,あくまでも,$${\bm{\omega}^T \dot{\bm{r}} = 0}$$が成り立つときで,これは点$${\text{P}}$$の速度ベクトル$${\dot{\bm{r}}}$$と剛体の角速度ベクトル$${\bm{\omega}}$$が垂直になるときで,それは点$${\text{P}}$$が点$${\text{o}}$$まわりに回転運動だけ行っているときにほかならない.そして,点$${\text{o}}$$は回転軸を通るひとつの点に過ぎず,剛体の瞬間回転を記述するものは軸(線分)であって,点ではないことを意味している.
さて,この式はあくまでも瞬間回転軸を通る点$${\text{o}}$$まわり式であるので,任意の座標系の原点$${\text{O}}$$からみた点$${\text{o}}$$の位置ベクトルを$${\bm{x}}$$,$${\text{O}}$$からみた点$${\text{P}}$$の位置ベクトルを$${\bm{p}}$$とすると
$$
\bm{p} = \bm{x} + \bm{r}
$$
なので,点$${\text{O}}$$からみて点$${\text{o}}$$が速度を持たず$${\dot{\bm{x}}=\bm{0}}$$なので
$$
\dot{\bm{p}} = \dot{\bm{x}} + \dot{\bm{r}} = \dot{\bm{r}}
$$
を満たす.これをベクトルの除法の結果に代入すると,
$$
\bm{p}-\bm{x} = \frac{(\dot{\bm{p}}-\dot{\bm{x}}) \times \bm{\omega}}{||\bm{\omega}||^2} = \frac{\dot{\bm{p}} \times \bm{\omega}}{||\bm{\omega}||^2}
$$
を得る.ここで$${c}$$は任意の定数で良いので,$${c=0}$$とした.
すると,
$$
\bm{x} = -\frac{\dot{\bm{p}} \times \bm{\omega}}{||\bm{\omega}||^2}+\bm{p} \\
= \frac{\bm{\omega} \times \dot{\bm{p}}}{||\bm{\omega}||^2}+\bm{p} \\
= \frac{[\bm{\omega} \times] \dot{\bm{p}}}{||\bm{\omega}||^2}+\bm{p}
$$
と書くことができ,$${\bm{x}}$$が瞬間回転軸が存在する線分のうちの一つの点を表す.
瞬間回転軸の回転軸方向は角速度ベクトル$${\frac{\bm{\omega}}{|| \bm{\omega} ||}}$$の方向なので,$${\bm{x}}$$を通り,$${\frac{\bm{\omega}}{|| \bm{\omega} ||}}$$方向の線分の点であればどこでも良いことになる.これを瞬間回転軸(screw axis,helical axis)と呼ぶ.瞬間回転軸の数学的な導出は文献4以外に文献5の最適化による導出方法もあり,両者を比較することで,より瞬間回転軸の物理的意味が明確になる.瞬間回転軸は回転の運動学における軸であるが,これの力学版が力の作用点(線)の定義となる.ご興味のある方は勉強されることをおすすめする.
ちなみに,似た概念に点の軌道に対する曲率中心(center of curvature)がある.これは剛体ではなく点の運動から定める.
瞬間回転軸を比較的容易に計算できることが理解できたと思う.ゴルフやバットや身体の軸の瞬間回転軸の変化を観察すると,運動の特徴(個人差)が現れる.ちなみにゴルフスイングのダウンスイング中,クラブの瞬間回転軸方向はほぼ一定で,軸がスイング中,平行移動するのが一般的である(○軸理論などあったが…).機会があればどこかで示していくが,ご興味があればお試しいただけたらと思う.
図7にプロゴルファーのダウンスイング中のクラブの瞬間回転軸の移動の例を示した.

補足4:ベクトルの除法の証明
文献4より引用
ベクトル方程式
$$
\bm{a} \times \bm{x} = \bm{b}~~~~~(\bm{a}\neq\bm{0})
$$
を満足するベクトル$${\bm{x}}$$が存在するための必要条件は
$$
\bm{a}^T \bm{b} = 0
$$
で,この時の解は
$$
\bm{x} = \frac{\dot{\bm{b}} \times \bm{a}}{||\bm{a}||^2} + c \bm{a}~~~~~(cは任意の定数)
$$
これをベクトル$${\bm{b}}$$をベクトル$${\bm{a}}$$で割ったベクトル商と呼び,第1項をその主ベクトルと呼ぶ.
証明:
一般に,$${\bm{x}}$$が存在するとすれば,
$$
\bm{a}^T \bm{b} = \bm{a}^T (\bm{a} \times \bm{x}) = 0
$$
ゆえに,$${\bm{a}^T \bm{b} = 0}$$は必要条件である.
もし$${\bm{a}^T \bm{b} = 0}$$とすれば,ベクトル三重積から
$$
\bm{a} \times (\bm{b} \times \bm{a}) = (\bm{a} ^T \bm{a}) \bm{b} - (\bm{a}^T \bm{b}) \bm{a} = (\bm{a}^T \bm{a}) \bm{b} = ||\bm{a}||^2 \bm{b}
$$
を得る.これで上式の両辺を割れば,
$$
\bm{a} \times \frac{\bm{b} \times \bm{a}}{|| \bm{a} ||^2} = \bm{b}
$$
となる.すなわち,$${\frac{\bm{b} \times \bm{a}}{|| \bm{a} ||^2}}$$は求める解の一つである.
次に,2つの解を$${\bm{x}_1, \bm{x}_2}$$とすれば
$$
\bm{a} \times \bm{x}_1 = \bm{b}, ~~\bm{a} \times \bm{x}_2 = \bm{b}\\
\therefore \bm{a} \times (\bm{x}_1 - \bm{x}_2) = \bm{0}
$$
ゆえに,$${\bm{x}_1 - \bm{x}_2}$$は$${\bm{a}}$$に平行であるから,$${c}$$を任意の定数とすれば,$${\bm{x}_1 - \bm{x}_2 = c\bm{a}}$$なので,一般解は
$$
\bm{x} = \frac{\dot{\bm{b}} \times \bm{a}}{\bm{a}^2} + c \bm{a}
$$
となる.
参考文献
1)Ge Wu et al. , ISB recommendation on definitions of joint coordinate system of various joints for the reporting of human joint motion--part I: ankle, hip, and spine. International Society of Biomechanics, Journal of Biomechanics, 35 (2002) 543–548.
2)Ge Wu et al. , ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion—Part II:
shoulder, elbow, wrist and hand, Journal of Biomechanics, 38 (2005) 981–992.
3)Plug-in Gait Reference Guide - Vicon Documentation
4)ベクトル解析,安達忠次著,培風館,1961(絶版であるが,ベクトルの除算について記述のある教科書は知る範囲ではこのぐらいである)
5)Flexible Multibody Dynamics: A Finite Element Approach, Michel Geradin , Alberto Cardona, Wiley, 2001(この書籍が示すように,ベクトルの除算を使用しなくても,瞬間回転軸は最適化の計算でも定まる)



【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
