
動かして学ぶバイオメカニクス#12 〜全身の力学解析(コード編)〜
このシリーズの目的を「関節に作用するトルクを計算すること」としたことを反省している.その計算コードの構築を通して,身体の力学の物理的意味を理解することと述べておけばよかった.いずれにせよ,オイラーの運動方程式を解きニュートン・オイラー法で並進力と回転力を計算する準備が整った.本章では,それをコードに落とす.このシリーズは,これで終わりではないが,一つの大きな区切りを迎えた.このPythonコードを正しく使いこなすには,あくまでもこれまで述べてきた内容の物理的・幾何学的意味,アルゴリズムの理解が不可欠である.しかし,コードの説明が不足していたと思われるが,お許し頂きたい.今後,過去にさかのぼって補足をしておくかもしれない.
動かして学ぶ関節トルクの計算
この章では,逆動力学計算に必要なコードが長いため,とりあえず,全コードを記述するだけとし,次章で補足する.
ここでは,全体が若干長いので,パッケージの読みや,ファイルの取り込みについては省略する.それらは,基本的には同じなので,過去の記事や,いつものように以下のGoogle Colaboratoryのリンクから,ブラウザでPythonコードを実行できるようにした.なお,ログインするためには,Googleアカウントが必要となるので注意をされたい.
また,使用するモーションキャプチャのサンプルデータ(sample_optitrack_221027.csv)とフォースプレートのサンプルデータ(sample_fp_221027.csv)は,このリンクからダウンロードして,Google Driveをマウントし,マウントしたドライブにそれらをコピーしてご使用いただきたい.これは,第6〜10章で使用したデータと同じであるので,すでにダウンロ度済みの方は,サイドダウンロードする必要はない.
Google Colaboratoryの使用方法は,
を参照されたい.
class BodyLinkの定義
以下は,すべての計算を含んでいるため,肥大化した.次章でピックアップして必要な部分を説明する.念の為,Googleアカウントのない方のために,以下に計算に必要なコードを全て記述する.
これまでの述べてきたが,次に示すclass BodyLinkのインスタンス変数(たとえば,w:角速度ベクトル, cg:重心の位置ベクトル)にはCの構造体のような役目,すなわち各種データを整理して格納しておく機能がある.また,メソッド(たとえば,ID_Newton():並進力の計算,ID_Euler():トルクの計算)には,インスタンス変数を利用した機能があり,ここでは力学計算を行う機能を担わせている.
力学計算はこのID_Newton()と,ID_Euler()が担い,身体の多体系の構造を二分木に落とし込み,それを利用した再帰呼び出しによる計算が基本となっている(二分木と再帰呼び出し,Pythonのクラスについては,第2章参照).再帰呼び出しによってニュートンの運動方程式を解く,ID_Newton()については第4章や第6章を参照されたい.ID_Euler()の基礎となる,オイラーの運動方程式については第7章や第11章を参照されたい.
##########################################################
# class BodyLink
##########################################################
class BodyLink:
def __init__(self, l_id:int, name:str, m_type:str, mass_ratio:float, cg_ratio:float):
self.l_id = l_id # linkのID
self.name = name # linkの名前
self.m_type = m_type # マーカの種類(Bone, Bone Marker, Marker)
self.mass_ratio = mass_ratio # linkの質量分配比
self.cg_ratio = cg_ratio # linkの重心位置の分配比
self.inertia_moment = None # linkの慣性モーメント
self.child_val = None # 子供の変数(ここではb_linkが格納される)
self.sister_val = None # 兄弟姉妹の変数(ここではb_linkが格納される)
self.distal_val = None # linkの遠位端の変数(ここではb_linkが格納される)
self.p = None # linkの関節の原点(近位端)
self.cg = None # linkの重心位置
self.acc = None # linkの重心の加速度
self.force = None # linkの関節に作用する力
self.ext_force = None # 外力(並進力が作用するlinkにだけ格納)
self.ext_moment = None # 外力(力のモーメントが作用するlinkにだけ格納.link原点まわりの絶対座標系)
self.rot = None # linkの姿勢行列
self.w = None # linkのローカル座標系の角速度ベクトル
self.dot_w = None # linkのローカル座標系の角加速度ベクトル
self.inertial_global = None # linkの慣性力によるトルク
self.j_moment_global = None # linkの相互作用(内力)によるトルク
self.tau_global = None # linkから遠位の総和のアクチュエータ由来のトルク(inertial_global + j_moment_global)
##########################################################
# 親子・姉妹関係
##########################################################
# BodyLinkを一旦作成してから,その後に親子,兄弟姉妹関係をBodyLinkに与える.
def set_child_sister(self, child_val, sister_val):
self.child_val = child_val
self.sister_val = sister_val
# リンク(部位)の重心を計算するためには,リンクの原点(近位端)と遠位端の位置ベクトルが必要
# ただし,末端のリンク(部位)には子供のリンク(部位)がないので,リンクの遠位端(関節)の情報を得られない
# BodyLinkを一旦作成してから,その後に,各リンクの遠位端の位置をBodyLinkに与える.親子関係とは区別して利用
def set_distal_end(self, distal_val):
self.distal_val= distal_val
##########################################################
############### Newton-Euler method ###############
##########################################################
##########################################################
# Newtonの運動方程式
##########################################################
# m * (acc - g)
def CgForce(self, bw):
gravity = [0., 0., -9.8] # 重力加速度ベクトル
return bw * self.mass_ratio * (self.acc - gravity)
# Inverse Dynamics Newton's equation of motion(再帰呼び出し)
#(★ 221221訂正)
def ID_Newton(self, bw, sister=False):
# 再帰呼び出しの終了条件1
# 末端のdistal endのext_force(外力)に外力(床反力等)が入力されている場合は,外力も取り込む
if np.any(self.ext_force) != None:
f = self.CgForce(bw) - self.ext_force #(★ 221221訂正)
self.force = f
return f
# 再帰呼び出しの終了条件2
# 外力が作用しない末端のlinkの遠位link(l_id == 0)は0
elif self.l_id == 0:
return 0.0
# 再帰呼び出しによる定義
elif sister == False: # 部分(そこから遠位:子供のみ)の解析
f = self.CgForce(bw)+\
self.child_val.ID_Newton(bw, sister)
self.force = f
return f
elif sister == True: # 全身解析(通常l_id=1を想定.兄弟姉妹を含む)
f = self.CgForce(bw)+\
self.child_val.ID_Newton(bw, sister)
self.force = f #(★ 221221訂正)
f_sister = f + self.sister_val.ID_Newton(bw, sister)
return f_sister
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
##########################################################
# Eulerの運動方程式
##########################################################
# 関節に作用する力のモーメント
#(★ 221221訂正)
def Joint_Moment_global(self):
# ★ 221221訂正)
# 末端のdistal endのext_momentに外力(フォースプレートのモーメント等)が入力されている場合は,外力も取り込む
#(ID_Joint_Moment_global()で外力を計算していたが,Joint_Moment_global()で外力を取り込むように変更
if np.any(self.ext_moment) != None:
return np.cross(self.p - self.cg, self.force) + self.ext_moment
# 近位側に作用する力のモーメント
elif np.any(self.child_val.force) == None:
return np.cross(self.p - self.cg, self.force)
# 近位側と遠位側の両方の関節に作用する力のモーメント
else:
return np.cross(self.p - self.cg, self.force) + \
np.cross(self.child_val.p - self.cg, -self.child_val.force)
# 力のモーメントを,その部位から遠位まで加算(再帰呼び出し)
# (★ 221221訂正)
def ID_Joint_Moment_global(self, sister=False):
# (★ 221221訂正)
# 再帰呼び出しの終了条件1
# 外力が作用しない末端のlinkの遠位link(l_id == 0)は0
if self.l_id == 0:
return 0.0
# 再帰呼び出しによる定義
elif sister == False: # 部分(そこから遠位のみの)解析
j_moment_global = self.Joint_Moment_global() + \
self.child_val.ID_Joint_Moment_global(sister)
self.j_moment_global = j_moment_global
return j_moment_global
elif sister == True: # 全身解析(通常l_id=1を想定.兄弟姉妹を含む)
inter_tau_local = self.Joint_Moment_global() + \
self.child_val.ID_Joint_Moment_global(sister)+ \
self.sister_val.ID_Joint_Moment_global(sister)
self.j_moment_global = j_moment_global
return j_moment_global
else:
print('Put True or False as sister option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# 慣性力(ローカル座標系)
def Inertial_Force_local(self):
return self.inertia_moment * self.dot_w + \
np.cross(self.w, self.inertia_moment * self.w)
# 慣性力(絶対座標系)
def Inertial_Force_global(self):
return frame_trans_global(self.rot,
self.inertia_moment * self.dot_w + \
np.cross(self.w, self.inertia_moment * self.w))
# 慣性力(絶対座標系)を,その部位から遠位まで加算(再帰呼び出し)
def ID_Inertial_Force_global(self, sister=False):
if self.l_id == 0:
return 0.0
elif sister == False: # l_idから遠位のみの部分解析
inertial_global = self.Inertial_Force_global() + \
self.child_val.ID_Inertial_Force_global(sister)
self.inertial_global = inertial_global
return inertial_global
elif sister == True: # 全身解析(通常l_id=1を想定.兄弟姉妹を含む)
inertial_global = self.Inertial_Force_global() + \
self.child_val.ID_Inertial_Force_global(sister)+ \
self.sister_val.ID_Inertial_Force_global(sister)
self.inertial_global = inertial_global
return inertial_global
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# 関節に作用するトルク
def Torque(self):
# linkの遠位端の関節に力が作用する場合
if np.any(self.child_val.force) != None:
return frame_trans_global(self.rot,
self.inertia_moment * self.dot_w +\
np.cross(self.w, self.inertia_moment * self.w)) -\
np.cross(self.p - self.cg, self.force) + \
np.cross(self.child_val.p - self.cg, self.child_val.force)
# linkの遠位端の関節に力が作用しない場合.
else:
return frame_trans_global(self.rot,
self.inertia_moment * self.dot_w +\
np.cross(self.w, self.inertia_moment * self.w)) -\
np.cross(self.p - self.cg, self.force)
# Inverse Dynamics Euler's equation of motion(再帰呼び出し)
# #(★ 2212121訂正)
def ID_Euler(self, sister=False):
# print(self.name)
if np.any(self.ext_moment) != None:
inertial_global = self.Inertial_Force_global()
j_moment_global = self.Joint_Moment_global()
tau_global = self.Torque() - self.ext_moment #(★ 221221訂正)
self.inertial_global = inertial_global
self.j_moment_global = j_moment_global
self.tau_global = tau_global
return tau_global
elif self.l_id == 0:
return 0.0
elif np.any(self.force == None):
print('Please evaluate ID_Newton() and calculate joint force')
# break
elif sister == False: # l_idから遠位のみの部分解析
inertial_global = self.Inertial_Force_global()
j_moment_global = self.Joint_Moment_global()
tau_global = self.Torque() + self.child_val.ID_Euler(sister)
self.inertial_global = inertial_global
self.j_moment_global = j_moment_global
self.tau_global = tau_global
return tau_global
elif sister == True: # 全身解析
inertial_global = self.Inertial_Force_global()
j_moment_global = self.Joint_Moment_global()
tau_global = self.Torque() + self.child_val.ID_Euler(sister) #(★ 2212121訂正)
tau_global_sister = tau_global + self.sister_val.ID_Euler(sister) #(★ 2212121訂正)
self.inertial_global = inertial_global
self.j_moment_global = j_moment_global
self.tau_global = tau_global #(★ 2212121訂正)
return tau_global_sister #(★ 2212121訂正)
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
##########################################################
# 合成の質量(全質量)の計算
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
# bw: 体重
##########################################################
def Resultant_Mass(self, bw, sister=False):
if self.l_id == 0:
return 0.0
elif sister == False: # 部分(そこから遠位のみの)解析
return bw * self.mass_ratio + (self.child_val).Resultant_Mass(bw, sister)
elif sister == True: # 全身解析
return (bw * self.mass_ratio +(self.child_val).Resultant_Mass(bw, sister) +
(self.sister_val).Resultant_Mass(bw, sister))
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# m * cg
def WeightedJoint(self, bw):
return bw * self.mass_ratio * self.cg
# 合成の(全)WeightedJoint
# Σ m_i * cg_i
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
def Resultant_WeightedJoint(self, bw, sister=False):
if self.l_id == 0:
return 0.0
elif sister == False: # 部分(そこから遠位のみの)解析
return self.WeightedJoint(bw)+\
(self.child_val).Resultant_WeightedJoint(bw, sister) #, sister)
elif sister == True: # 全身解析
return self.WeightedJoint(bw)+\
self.child_val.Resultant_WeightedJoint(bw, sister)+\
self.sister_val.Resultant_WeightedJoint(bw, sister)
else:
print('Put True or False as sister (2nd) option')
print('If sister == True, this calculate also sister tree')
print('If sister == False (default), this calculate only child tree')
# 合成重心
# Resultant_WeightedJoint() / Resultant_Mass()
# = Σ(m_i * cg_i) / Σ m_i
# sister == False なら,部分解析(そのリンクの遠位側だけ計算)
# sister == True なら,全身解析(兄弟を含める)
def Resultant_Cg(self, bw, sister=False):
return self.Resultant_WeightedJoint(bw, sister)/self.Resultant_Mass(bw, sister)BodyLinkクラスの配列の初期化
以下で代入されている,身体各部位の質量を決めるパラメータmass_ratioや,重心位置を決めるパラメータcg_ratioについては第3章を参照されたい.
b_link = [0] * 27 # 配列の初期化
b_link[0] = BodyLink(0, '', '', .0, .0) # 0のときストップ
b_link[1] = BodyLink(1, 'Hip', 'Bone', .187, (1.-.609)) # 腰(下体幹)
b_link[2] = BodyLink(2, 'Chest', 'Bone', .302, (1.-.428)) # 胸(上体幹)
b_link[3] = BodyLink(3, 'Neck', 'Bone', .069, (1.-.821)) # 頭部
b_link[4] = BodyLink(4, 'RUArm', 'Bone', .027, .529) # 右上腕
b_link[5] = BodyLink(5, 'RFArm', 'Bone', .016, .415) # 右前腕
b_link[6] = BodyLink(6, 'RHand', 'Bone', .006, .891) # 右手
b_link[7] = BodyLink(7, 'LUArm', 'Bone', .027, .529) # 左上腕
b_link[8] = BodyLink(8, 'LFArm', 'Bone', .016, .415) # 左前腕
b_link[9] = BodyLink(9, 'LHand', 'Bone', .006, .891) # 左手
b_link[10] = BodyLink(10, 'RThigh', 'Bone', .110, .475) # 右大腿
b_link[11] = BodyLink(11, 'RShin', 'Bone', .051, .406) # 右下腿
b_link[12] = BodyLink(12, 'RFoot', 'Bone', .011, (1.-.595)) # 右足
b_link[13] = BodyLink(13, 'LThigh', 'Bone', .110, .475) # 左大腿
b_link[14] = BodyLink(14, 'LShin', 'Bone', .051, .406) # 左下腿
b_link[15] = BodyLink(15, 'LFoot', 'Bone', .011, (1.-.595)) # 左足
# 各リンクの遠位端も定義(遠位端の位置ベクトルを計算するためだけに必要な変数
b_link[16] = BodyLink(16, 'Head', 'Bone', .0, .0) # 3 Neckの遠位端
b_link[17] = BodyLink(17, 'RFIN', 'Bone Marker',.0, .0) # 6 RHandの遠位端
b_link[18] = BodyLink(18, 'LFIN', 'Bone Marker', .0, .0) # 9 LHandの遠位端
b_link[19] = BodyLink(19, 'RToe', 'Bone', .0, .0) # 12 RFootの遠位端
b_link[20] = BodyLink(20, 'LToe', 'Bone', .0, .0) # 15 LFootの遠位端
# 手,前腕の姿勢回転行列を計算するためだけに必要な変数
b_link[21] = BodyLink(21, 'RWRA', 'Bone Marker', .0, .0) # 右手首橈骨側
b_link[22] = BodyLink(22, 'RWRB', 'Bone Marker', .0, .0) # 右手首尺骨側
b_link[23] = BodyLink(23, 'LWRA', 'Bone Marker', .0, .0) # 左手首橈骨側
b_link[24] = BodyLink(24, 'LWRB', 'Bone Marker', .0, .0) # 左手首尺骨側
b_link[25] = BodyLink(25, 'RFHD', 'Bone Marker', .0, .0) # 右前頭
b_link[26] = BodyLink(26, 'LFHD', 'Bone Marker', .0, .0) # 左前頭力学計算のためのその他の関数群
以下の関数は,前述のclass BodyLinkの各インスタンス変数にデータを格納したり,その計算を補助する関数である.
rotを利用したベクトルの座標変換
# 方向余弦を並べた配列rot_vecから → 姿勢回転行列の配列へ変換
def rot_vec2mat_local(rot_vec):
return np.array([rot_vec[:,i] for i in range(len(rot_vec[0]))])
def rot_vec2mat_global(rot_vec):
return np.array([rot_vec[:,i].T for i in range(len(rot_vec[0]))])
def trans_frame(rot, vec):
return np.squeeze(rot @ vec[:,:,np.newaxis])
# 方向余弦を並べた配列rot_vecを使用して,ベクトルvecを絶対座標系に変換
def frame_trans_global(rot_vec, vec):
return np.squeeze(rot_vec2mat_global(rot_vec) @ vec[:,:,np.newaxis])
# 方向余弦を並べた配列rot_vecを使用して,ベクトルvecを絶対座標系からローカル座標系に変換
def frame_trans_local(rot_vec, vec):
return np.squeeze(rot_vec2mat_local(rot_vec) @ vec[:,:,np.newaxis])数学関数
# ノルム(大きさ)
def norm(vec_array):
return np.linalg.norm(vec_array, axis=1)
# 単位ベクトル
def unit_vec(data_vec):
data_norm = np.linalg.norm(data_vec, axis=1)[:,np.newaxis]
return data_vec/data_norm
# 内積
# 時系列のベクトル(2次元配列)のa_arrayとb_arrayの「内積」を時系列(2次元配列)として出力
def dot_array(a_array, b_array):
return np.sum(a_array * b_array, axis=1)平滑化スプライン(第5章参照)
# 微分と平滑化を同時にスプライン平滑化で行う
# 4次の自然スプライン(加速度計算を考慮)
# order=0:変位(時間微分なし),order=1:速度, order=2:加速度
def smoothing_spline(vec_data, weight, sf, order=0, degree=4):
vec_copy = copy.copy(vec_data)
vec_data_t = vec_copy.T
len_num = len(vec_data)
len_vec = len(vec_data_t)
time = np.arange(0, len_num) / sf
w_a = [np.isnan(x) for x in vec_data_t]
spl = [0]*len_vec
for i in range(len_vec):
vec_data_t[i][w_a[i]] = 0.
w_a[i] = ~w_a[i]
spl[i] = UnivariateSpline(time, vec_data_t[i], w_a[i], s=weight, k=degree).derivative(n=order)(time)
return np.array(spl).Tmotion capture の csv file からデータ抽出
motion captureのデータからマーカの位置ベクトルを抽出
# CSVデータからヘッダだけ抽出
def extract_df_header(file_path):
return pd.read_csv(file_path, header=None, nrows=5, index_col=1).T
# skeletonの名前を抽出
def extract_skeleton_name(file_path):
df = extract_df_header(file_path)
marker_name = df['Name'][2]
position_col = marker_name.find(':')
return marker_name[:position_col]
# ファイル名,マーカ名,マーカタイプを引数に与えて各Linkの重心の加速度データを抽出する関数
# marker_typeとして,'Bone'(default), 'Bone Marker, 'Marker' を選択できるように修正
def extract_marker(file_path, marker_name, marker_type='Bone'):
sk_name = extract_skeleton_name(file_path) # skeleton
df_main = pd.read_csv(file_path, header=[4]) # データだけ抽出
df = extract_df_header(file_path) # headerだけ抽出
df_selected = df[(df['Type']==marker_type) & (df['Name']== sk_name+':'+marker_name)] # ヘッダがNameとTypeの両方が一致する部分だけ抽出
selected_rows = df_selected.index # 一致する列
marker_data = np.array(df_main.iloc[:, selected_rows[-3:]].values) # 後ろから3個データを取得す
return marker_data[:, [2,0,1]] # OptiTrackの座標がYup(Y軸が上)のため,座標を入れ替えることで,Zupに変更するforce plate の csv file から力と力のモーメントなどのデータ抽出
force plateのデータから,力とモーメントのデータを,force plateの番号(1, 2)と,ch(Fx, Fy, Fz, Mx, My, Mz)を指定して抽出する.
force plate座標系 → motion capture座標系への変換を行う
# Force PlateのCSVデータから指定したchのデータを抽出
# ファイル名とchの名前を引数に与えて力または力のモーメントとCOPを抽出する関数
# fp_num:1 or 2(1: 左,2:右)
# fp_ch:'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz','ax', 'ay'から選択
# force plate 座標系からmotion capture座標系に変換
def extract_fp(file_path_fp, fp_num:int=1, fp_ch:str='Fx'):
df = pd.read_csv(file_path_fp, skiprows=[0,2,3,4,5])
fp_name_list = np.unique([x[0:4] for x in df.columns[1:]]) # force plateの名前のリストを抽出
header = fp_name_list[fp_num-1] + '-' + fp_ch
# force plateの座標をmotion captureの座標に変換し出力
if fp_ch == 'Fx' or fp_ch == 'Mx' or fp_ch == 'ay':
return -df[header].values
else:
return df[header].values
# forceとmomentのベクトル,COPの位置ベクトル,摩擦モーメントとして出力
# fp_num:1 or 2 (1: 左,2:右)
# fp_type:'f', 'm','c', 'tz'から選択('f':force,'m':moment, 'c': COP, 'tz': frictional moment)
def extract_fp_vec(file_path_fp, fp_num:int=1, fp_type:str='f'):
fp_x_size = 600. # force plateのx方向の大きさ [mm]
fp_y_size = 900. # force plateのy方向の大きさ [mm]
if fp_type == 'f':
return np.array([extract_fp(file_path_fp, fp_num, 'Fx'), extract_fp(file_path_fp, fp_num, 'Fy'),
extract_fp(file_path_fp, fp_num, 'Fz')]).T
elif fp_type == 'm':
return np.array([extract_fp(file_path_fp, fp_num, 'Mx'), extract_fp(file_path_fp, fp_num, 'My'),
extract_fp(file_path_fp, fp_num, 'Mz')]).T
elif fp_type == 'c':
if fp_num == 1:
return np.array([extract_fp(file_path_fp, fp_num, 'ax') + fp_x_size/2., extract_fp(file_path_fp, fp_num, 'ay') + fp_y_size/2.]).T/1000.
elif fp_num == 2:
return np.array([extract_fp(file_path_fp, fp_num, 'ax') - fp_x_size/2., extract_fp(file_path_fp, fp_num, 'ay') + fp_y_size/2.]).T/1000.
elif fp_type == 'tz':
return extract_fp(file_path_fp, fp_num, 'Tz')[:,np.newaxis]床反力(地面反力)
フォースプレートとモーションキャプチャのサンプリングレートが異なるため,スプライン補間を利用し,リサンプリング(サンプリングレートの変換)を行う.
# リサンプリング(サンプリングレートの変換)のためにUnivariateSpline()を使用
# 重み係数s=0とすることで,平滑化を行わず,補間
def spline_interpoation(vec_data, sf_original=1000., sf_new=360.):
vec_copy = copy.copy(vec_data)
vec_data_t = vec_copy.T
len_num = len(vec_data)
len_vec = len(vec_data_t)
rate = sf_new / sf_original
time_old = np.arange(0, len_num) / sf_original
time_new = np.arange(0, len_num * rate)/(sf_original * rate)
w_a = [np.isnan(x) for x in vec_data_t]
spl = [0] * len_vec
for i in range(len_vec):
vec_data_t[i][w_a[i]] = 0.
w_a[i] = ~w_a[i]
spl[i] = UnivariateSpline(time_old, vec_data_t[i], w_a[i], s=0, k=3)(time_new)
return np.array(spl).T
# サンプリングレート 1kHzのforce plateのデータを
# motion caputreのサンプリングレート(360Hz)に合わせて変換(リサンプリング)
# UnivariateSpline()を使用.重み係数s=0とすることで,平滑化を行わず,補間
def fp_interpolation(file_path_fp, fp_num:int=1, fp_type:str='f', sf_original=1000., sf_new=360.):
fp_vec = extract_fp_vec(file_path_fp, fp_num, fp_type)
return spline_interpoation(fp_vec, sf_original, sf_new)
# リサンプリングと座標変換(座標変換はextract_fp()で行う)
# モーションキャプチャのデータの長さが必要なため,モーションキャプチャのデータのファイルパスも必要
def fp2op_frame(file_path_fp, file_path_op, fp_num:int=1, fp_type:str='f', sf_original=1000., sf_new=360.):
op = extract_marker(file_path_op, 'RHand') # 右手データを使用(何でも良い)
len_op = len(op) # モーションキャプチャのデータの長さ
fp = fp_interpolation(file_path_fp, fp_num, fp_type, sf_original, sf_new)
return fp[0:len_op]以下の関数は,この計測データ限定の関数(COPと足関節の距離などから,接地するfpの判断は可能だが,複雑なので,ここでは簡略的に指定)で,計測や実験に応じて,各自で作り変える必要があるので注意されたい.
フォースプレートの位置は,フォースプレートの幾何学依存,モーションキャプチャの計測環境依存なので,この実験にのみ有効な関数となっている.
ここでは,右足がforce palte 2に,左足がforce plate 1に接地する前提で作られている.
# (★ 221221訂正)linkの原点 → linkの重心
# force plateのモーメントをlink(link_idで指定)の重心まわりのモーメントに変換
# 正確にはlink_idの遠位側(distal_val)に作用する力
# fp_x_size = .6 # force plateのx方向の大きさ [mm]
# fp_y_size = .9 # force plateのy方向の大きさ [mm]
# fp_z_origin = -.045 force plateの原点の方向成分
def moment2link(file_path_fp, file_path_op, link_id, sf_original=1000., sf_new=360., fp_x_size=.6, fp_y_size = .9, fp_z_origin=-.045):
op = extract_marker(file_path_op, 'RHand') # motion captureデータ:右手データを使用(何でも良い)
len_op = len(op) # モーションキャプチャのデータの長さ
if link_id == 12:
fp_num = 2
fp_origin = [-fp_x_size/2., fp_y_size/2., fp_z_origin] # motion captureの原点座標
elif link_id == 15:
fp_num = 1
fp_origin = [fp_x_size/2., fp_y_size/2., fp_z_origin]
moment_fp_frame = fp2op_frame(file_path_fp, file_path_op, fp_num, 'm', sf_original, sf_new)
moment_link_frame = np.cross(fp_origin - b_link[link_id].cg, b_link[link_id].ext_force) + moment_fp_frame # (★ 221221訂正)
return moment_link_frame親子関係(child_val),兄弟姉妹関係(sister_val),遠位端(distal_val)(第2章参照)
# 親子関係と兄弟姉妹関係を下記でb_linkのchild_val, sister_valに追記
child_sister_list = [
[1,2,0], [2,3,10], [3,0,4], [4,5,7], [5,6,0], [6,0,0], [7,8,0],
[8,9,0], [9,0,0], [10,11,13], [11,12,0], [12,0,0], [13,14,0],
[14,15,0], [15,0,0]]
# 各リンクの遠位端の情報を格納.b_linkのcdistal_valに追記
distal_end_list = [
[1,2], [2,3], [3,16], [4,5], [5,6], [6,17], [7,8],
[8,9], [9,18], [10,11], [11,12], [12,19], [13,14],
[14,15], [15,20], [16,0], [17,0], [18,0], [19,0], [20,0]]各リンクの原点(p)(第9章参照)
各部位の位置ベクトルをCSVファイルから読み込む.
部位の原点に相当するマーカの名前は,クラスから指定する.
# リンクの原点の位置ベクトル
def joint_vec(b_link, l_id, path):
if l_id == 0:
return .0
else:
joint_name = b_link[l_id].name
joint_type = b_link[l_id].m_type
return extract_marker(path, joint_name, joint_type) 位置ベクトルpにも,速度や加速度ベクトルの計算と同様に,平滑化スプラインでフィルタリングする(平滑化スプラインについては,第5章参照)
# 関節位置をBodyLinkクラスに格納
# 部位を指定し,関節位置ベクトルを計算し,BodyLinkのpに格納する関数
def set_link_p_list(b_link, l_id_list, path, weight = .00001, sf = 360.):
for n in l_id_list:
b_link[n].p = smoothing_spline(joint_vec(b_link, n, path), weight, sf, order=0)手,前腕の姿勢回転行列を計算するためだけに必要なマーカの位置ベクトルをインスタンス変数pに格納
# 手と前腕の姿勢回転行列を計算する際に,補助的に必要な手首の両側のマーカRWRA, RWRB, LWRA, LWRBをBodyLinkクラスに格納
def set_rot_p_list(b_link, l_id_list, path, weight = .00001, sf = 360.):
for n in l_id_list:
joint_name = b_link[n].name
joint_type = b_link[n].m_type
marker_vec = extract_marker(path, joint_name, joint_type)
b_link[n].p = smoothing_spline(marker_vec, weight, sf, order=0)各部位の重心の加速度ベクトル(acc)
各リンクの重心の加速度ベクトルを格納する前に,各リンクの重心の位置ベクトルを計算する.身体各部位の重心位置については第3章参照されたい.
def link_cg(b_link, l_id, path, weight = .0001, sf = 360.):
div_p = b_link[l_id].cg_ratio
body_q = joint_vec(b_link, l_id, path)
body_distal_q = joint_vec(b_link, b_link[l_id].distal_val.l_id, path)
cg = (1-div_p) * body_q + div_p * body_distal_q
return smoothing_spline(cg, weight, sf, order=0)各リンクの重心の加速度ベクトルをインスタンス変数accに格納
# 各linkの重心位置ベクトルから,重心の加速度ベクトルを計算
def set_acc(b_link, l_id, weight = .00001, sf = 360.):
b_link[l_id].acc = smoothing_spline(b_link[l_id].cg, weight, sf, order=2)
# それを,self.accに格納
def set_acc_link(b_link, l_id_list, weight = .00001, sf = 360.):
np.array([set_acc(b_link, n, weight, sf) for n in l_id_list])各部位の長さ
# 以下の慣性モーメントの計算で必要
def link_length(b_link, link_id):
return norm(b_link[b_link[link_id].distal_val.l_id].p - b_link[link_id].p)慣性モーメント(第8章参照)
# 慣性モーメントを計算するためのパラメータ: para[0]*bw + para[1]*link_length + para[2]
# これらで計算した結果の慣性モーメントの単位は kg cm^2なので,10^(-4)をかけてkg m^2に変換する必要がある
# 0:左右軸,1:前後軸,2:長軸
# 男子用
i_m_para0 = [[.0, .0, .0], [.0, .0, .0], [.0, .0, .0]]
i_m_para1 = [[22.62, 5588.38, -1687.06], [27.7 , 6516.01, -1982.55],[29.08, 2246.6 , -1376.85]] # HIP(下胴)
i_m_para2 = [[58.01, 15247.8 , -6157.42], [71.52, 15063., -6423.4 ], [48.9 , 1516.61, -2016.55]] # Chest(上胴)
i_m_para3 = [[2.71, 2843.24, -367.9], [2.49, 2681.7 , -354.1 ], [1.25, 1307.37, -138.96]] # NECK(頭部)
i_m_para4_7 = [[1.85, 1007.85, -317.68], [1.74, 999.69, -312.14], [0.71, -44.88, -11.1]] # UpperArm(上腕)
i_m_para5_8 = [[0.86, 562.22, -145.87], [0.8, 576.66, -146.45], [0.24, 26.38, -13.48]] # Fore Arm(前腕)
i_m_para6_9 = [[ 0.11, 80.36, -6.37], [0.14, 82.07, -7.31], [0.05, 9.08, -1.67]] # Hand(手)
i_m_para10_13 = [[11.83, 5684.2 , -2127.91], [10.65, 5547.75, -2043.38], [6.63, 418.34, -350.31]] # Thigh(大腿)
i_m_para11_14 = [[5.27, 3093.33, -1190.24], [5.19, 3048.1, -1174.66], [1.11, 104.75, -62.79]] # Sin(下腿)
# 0:左右(関節)軸,1:上下軸,2:長軸
i_m_para12_15 = [[ 0.01, 214.58, -38.93], [0.01, 228.14, -40.98], [0.01, 37.67, -6.3 ]] # Foot(足)
inertia_para_dict_m = {1:i_m_para1, 2:i_m_para2, 3:i_m_para3,
4:i_m_para4_7, 5:i_m_para5_8, 6:i_m_para6_9, 7:i_m_para4_7, 8:i_m_para5_8, 9:i_m_para6_9,
10:i_m_para10_13, 11:i_m_para11_14, 12:i_m_para12_15, 13:i_m_para10_13, 14:i_m_para11_14, 15:i_m_para12_15}
# 女子用
i_w_para0 = [[.0, .0, .0], [.0, .0, .0], [.0, .0, .0]]
i_w_para1 = [[19.08, 5368.76, -1407.99], [25.86, 7013.95, -1884.32], [27.44, 3909.55, -1472.05]] # HIP(下胴)
i_w_para2 = [[36.67, 10495.1 , -3537.95], [44.82, 10796.7 , -3751.31], [33.43, 1489.2 , -1214.28]] # Chest(上胴)
i_w_para3 = [[2.03, 2109.44, -234.04], [1.81, 1973.49, -224.25], [0.97, 1085.02, -98.47]] # NECK(頭部)
i_w_para4_7 = [[1.28, 888.26, -243.45], [1.13, 890.14, -239.38], [0.46, 16.56, -15.05]]# UpperArm(上腕)
i_w_para5_8 = [[0.53, 387.15, -85.15], [0.49, 401.2, -86.13], [0.14, 22.58, -6.2 ]] # Fore Arm(前腕)
i_w_para6_9 = [[0.1 , 68.32, -6.56], [0.14, 69.02, -6.67], [0.04, 8.99, -1.07]] # Hand(手)
i_w_para10_13 = [[19.53, 4292.37, -1895.67], [17.66, 4347.35, -1851.78], [9.01, -14.12, -262.08]] # Thigh(大腿)
i_w_para11_14 = [[4.82, 2373.89, -840.81], [4.76, 2342.82, -830.82], [1.17, 67.14, -46.44]] # Sin(下腿)
# 0:左右(関節)軸,1:上下軸,2:長軸
i_w_para12_15 = [[0.14, 148.98, -30.67], [0.16, 153.66, -32.22], [0.04, 31.2, -6.5]] # Foot(足)
inertia_para_dict_w = {1:i_w_para1, 2:i_w_para2, 3:i_w_para3,
4:i_w_para4_7, 5:i_w_para5_8, 6:i_w_para6_9, 7:i_w_para4_7, 8:i_w_para5_8, 9:i_w_para6_9,
10:i_w_para10_13, 11:i_w_para11_14, 12:i_w_para12_15, 13:i_w_para10_13, 14:i_w_para11_14, 15:i_w_para12_15}
# 部位に対応するパラメータ,その部位の長さ,体重を与えて,慣性モーメントを計算
def inertia_moment(i_para, body_weight, ave_link_length):
return np.array([i_para[i][0]*body_weight + i_para[i][1]*ave_link_length + i_para[i][2] for i in range(3) ])*(10.**(-4))姿勢回転行列(座標軸 rot)の定義・格納(第9章参照)
以下の辞書に,座標軸の計算方法種類,その計算に必要なマーカの情報を格納する.
# 各リンクの座標軸を計算するための辞書情報
# [linkのID, [軸計算方法の種類, [マーカ名1, マーカ1のタイプ],[マーカ名2, マーカ2のタイプ],[]]]
# 順番に注意
frame_dict = dict([
[1, [1, 2, 10, 13]], # 腰(下体幹) method1
[2, [2, 3, 4, 7]], # 胸(上体幹) method1
[3, [3, 16, 25, 26]], # 胸(上体幹) method1
[4, [4, 5, 6]], # 右上腕 method2
[5, [5, 6, 21, 22]], # 右前腕 method1
[6, [6, 17, 21, 22]], # 右手 method1
[7, [7, 8, 9]], # 左上腕 method2
[8, [8, 9, 24, 23]], # 左前腕 method1
[9, [9, 18, 24, 23]], # 左手 method1 (順番に注意)
[10, [10, 11, 12]], # 右大腿 method2
[11, [10, 11, 12]], # 右下腿 method2
[12, [11, 12, 19]], # 右足 method2
[13, [13, 14, 15]], # 左大腿 method2
[14, [13, 14, 15]], # 左下腿 method2
[15, [14, 15, 20]] # 左足 method2
])以下の関数で,各リンクの姿勢回転行列(座標軸)を計算,格納する.
# bodylinkと部位のl_idを指定し,各linkの姿勢行列を計算し,インスタンスrotに格納
def set_frame(b_link, l_id, frame_dict):
method1 = [1, 2, 3, 5, 6, 8, 9]
method2 = [4, 7, 10, 11, 12, 13, 14, 15]
f_dict = frame_dict[l_id]
if any(l_id == elem for elem in method1):
b_link[l_id].rot = frame_method1(f_dict[0], f_dict[1], f_dict[2], f_dict[3])
elif any(l_id == elem for elem in method2):
b_link[l_id].rot = frame_method2(f_dict[0], f_dict[1], f_dict[2], l_id)
else:
print('error')
def set_frame_link(b_link, l_id_list, frame_dict):
for n in l_id_list:
set_frame(b_link, n, frame_dict)部位で姿勢回転行列の計算方法が異なる(2種類)
# 2つの位置ベクトルの差分
# origin, headの順番で指定
def diff_joint_vec(j_origin_id, j_head_id):
return b_link[j_head_id].p - b_link[j_origin_id].p
# 手,前腕の座標系
# 手首の外・橈骨側マーカA,内・尺骨側マーカB を利用
# 左右で以下のマーカの順番が異なるので注意.右はRWRA, RWRBの順で指定.左はLWRB, LWRAの順で指定
# x軸:蝶番関節方向
# z:長軸,y:前後方向
# z軸は近位から遠位方向なので,右は回外,左は回内に相当
def frame_method1(j_origin_id, j_head_id, j_right_id, j_left_id):
joint_unit_axis_z = unit_vec(diff_joint_vec(j_origin_id, j_head_id))
joint_axis_x = diff_joint_vec(j_right_id, j_left_id)
joint_unit_axis_y = unit_vec(np.cross(joint_unit_axis_z, joint_axis_x))
joint_unit_axis_x = np.cross(joint_unit_axis_y, joint_unit_axis_z)
return np.array([joint_unit_axis_x, joint_unit_axis_y, joint_unit_axis_z])
# 上腕,大腿,下腿,足の座標系
# 3つの関節中心座標が計算に必要
# x軸:蝶番関節方向(伸展屈曲軸)
# z:長軸,y:前後方向
def frame_method2(j1_list, j2_list, j3_list, joint_id=4):
joint_unit_axis_z1 = unit_vec(diff_joint_vec(j1_list, j2_list)) # z1: joint1 → joint2
joint_unit_axis_z2 = unit_vec(diff_joint_vec(j2_list, j3_list)) # z2: joint2 → joint3
# 関節の構造と外積の性質から,部位によって左右軸のx軸の向きが変化する(注意:過伸展に未対応)
lst1 =[4, 7, 12, 15]
lst2 =[10, 13, 11, 14]
if any(joint_id == elem for elem in lst1):
pm = -1.
elif any(joint_id == elem for elem in lst2):
pm = 1.
joint_unit_axis_x = pm * unit_vec(np.cross(joint_unit_axis_z1, joint_unit_axis_z2))
lst3 =[4, 7, 10, 13]
lst4 =[11, 14, 12, 15]
if any(joint_id == elem for elem in lst3):
joint_unit_axis_y = np.cross(joint_unit_axis_z1, joint_unit_axis_x) # y1軸
return np.array([joint_unit_axis_x, joint_unit_axis_y, joint_unit_axis_z1])
elif any(joint_id == elem for elem in lst4):
joint_unit_axis_y = np.cross(joint_unit_axis_z2, joint_unit_axis_x) # y2軸
return np.array([joint_unit_axis_x, joint_unit_axis_y, joint_unit_axis_z2])角速度・角加速度ベクトル(第10章参照)
# 角速度:単位ベクトルの速度と,直交する方向の単位ベクトルとの内積で計算
def angular_velocity(bases, weight, sf):
dot_bases = np.array([smoothing_spline(bases[i], weight, sf, order=1) for i in range(3)])
return np.array([dot_array(dot_bases[1], bases[2]),
dot_array(dot_bases[2], bases[0]),
dot_array(dot_bases[0], bases[1])]).T
# 角加速度:角速度の微分
def angular_acceleration(bases, weight, sf):
dot_bases = np.array([smoothing_spline(bases[i], weight, sf, order=1) for i in range(3)])
w = np.array([dot_array(dot_bases[1], bases[2]),
dot_array(dot_bases[2], bases[0]),
dot_array(dot_bases[0], bases[1])]).T
dot_w = smoothing_spline(w, weight, sf, order=1)
return dot_w
# 角速度と各加速度を同時に計算
def angular_vel_acc(bases, weight, sf):
dot_bases = np.array([smoothing_spline(bases[i], weight, sf, order=1) for i in range(3)])
w = np.array([dot_array(dot_bases[1], bases[2]),
dot_array(dot_bases[2], bases[0]),
dot_array(dot_bases[0], bases[1])]).T
dot_w = smoothing_spline(w, weight, sf, order=1)
return w, dot_w# b_inkと部位のl_idを指定し,各linkの姿勢行列(rot)から角速度を計算,格納
def set_w_dotw(b_link, l_id, weight=.0001, sf=360.):
av, aa = angular_vel_acc(b_link[l_id].rot, weight, sf)
b_link[l_id].w = av
b_link[l_id].dot_w = aa
def set_w_dotw_link(b_link, l_id_list, weight=.0001, sf=360.):
for n in l_id_list:
set_w_dotw(b_link, n, weight, sf)Preprocessing・準備
機械学習の前処理(Preprocessing)とは意味が異なるが,以下でBodyLinkクラスの配列b_linkの各インスタンス変数にデータを格納することで,ニュートン・オイラー法による力学計算の準備を行う.
親子関係(child_val),兄弟姉妹関係(sister_val),遠位端(distal_val)
[b_link[i[0]].set_child_sister(b_link[i[1]], b_link[i[2]]) for i in child_sister_list];
[b_link[i[0]].set_distal_end(b_link[i[1]]) for i in distal_end_list];linkの原点の位置ベクトル(p)
手,前腕の姿勢回転行列を計算するためだけに必要なマーカの位置ベクトルもインスタンス変数pに格納する.
# 関節位置をBodyLinkのpに格納
set_link_p_list(b_link, range(1,21), file_path_op_12, .00005, 360.)
# 姿勢回転行列を計算するために必要なマーカ位置ををBodyLinkのl_id: 21~24のpに格納
set_rot_p_list(b_link, range(21,27), file_path_op_12, .00005, 360.)重心の位置ベクトル(cg)
各リンクの重心の加速度ベクトルを格納する前に,各リンクの重心の位置ベクトルcgを計算する.
# 各linkの重心を,self.cgに格納
for n in range(1,16):
b_link[n].cg = link_cg(b_link, n, file_path_op_12, .00005, 360.)重心の加速度ベクトル(acc)
各リンクの重心の加速度ベクトルをインスタンス変数accに格納する.
# 各linkの重心の加速度ベクトルをself.accに格納
set_acc_link(b_link, range(1,16), .00005, 360.)床反力(ext_force)
左右の足の遠位端のインスタンス変数forceに,床反力を格納する.
b_link[12].ext_force = fp2op_frame(file_path_fp_12, file_path_op_12, 2, 'f')
b_link[15].ext_force = None # fp2op_frame(file_path_fp_12, file_path_op_12, 1, 'f')姿勢回転行列(rot)
set_frame_link(b_link, range(1,16), frame_dict)角速度ベクトル(w)
# 角速度と角加速度をw, dot_wに格納
set_w_dotw_link(b_link, range(1,16), weight=.0005, sf=360.)床反力(力のモーメント)(ext_moment)
左右の足の遠位端のインスタンス変数forceに,床反力を格納する.
左右の足の遠位端のインスタンス変数tau_globalに,足の原点まわりに変換した力のモーメントを格納する.
b_link[12].ext_moment = moment2link(file_path_fp_12, file_path_op_12, 12)
b_link[15].ext_moment = None #moment2link(file_path_fp_12, file_path_op_12, 15)慣性モーメント(inertia_moment)
各部位の長さ
# 各部位の長さの平均
b_length = [np.average(link_length(b_link, i)) for i in range(1,16)]インスタンス変数inertia_momentに格納
# 体重86.0kgの被験者の慣性モーメントをb_linkのクラスのinertia_momentに格納
bw = 86.
for l_id in range(1,16):
b_link[l_id].inertia_moment = inertia_moment(inertia_para_dict_m[l_id], bw, b_length[l_id-1])力学計算の例
以上のclass BodyLinkの定義,補助関数の定義,前処理を行うことで,力学計算の準備が整った.
具体的な計算例は次章で述べるが,ここでは,これらを利用し全身の関節に作用する力とトルクの計算を行う.
ここで使用するデータは,踏み台から,フォースプレートに右脚で飛び降りた例である.
関節に作用する力(ニュートンの運動方程式)の計算
class BodyLinkのメソッドID_Newton()は逆動力学計算により,各linkの並進力を計算し,配列b_link[i](i = 2〜15),すなわち各部位の原点(関節)に作用する並進力を b_link[i].forceに代入する.
全linkの頂点である,b_link[1]に対して,sisiter=Trueのオプションを与えることで,全リンクの関節に作用する力を計算する.
もし,b_link[2].ID_Newton(86., True)とすれば,上半身(Chest以下のlink)に対してだけ計算する.下肢に対してだけ力学計算を行うには,少々コードの修正が必要となるが,練習問題として残しておく.再帰呼び出し,二分木を理解していれば,それほど難しくないはずである.
ニュートンの運動方程式を利用した,関節に作用する力の解法については
や
を参照されたい.
b_link[1].ID_Newton(86., True)関節に作用するトルク(オイラーの運動方程式)の計算
注意! 事前に,b_link[1].ID_Euler(True) の評価が必須(関節に作用する力をオイラーの運動方程式の計算に必要とする).
b_link[1].ID_Euler(True)ここでは,一例だけ示す.右膝関節に作用するトルクを確認する.
tau_r_knee = b_link[11].tau_global
t_list = np.arange(len(tau_r_knee))/360.
plt.plot(t_list, tau_r_knee)
plt.xlabel('Time [s]')
plt.ylabel('Torque [Nm]')
plt.legend(['x', 'y:', 'z'])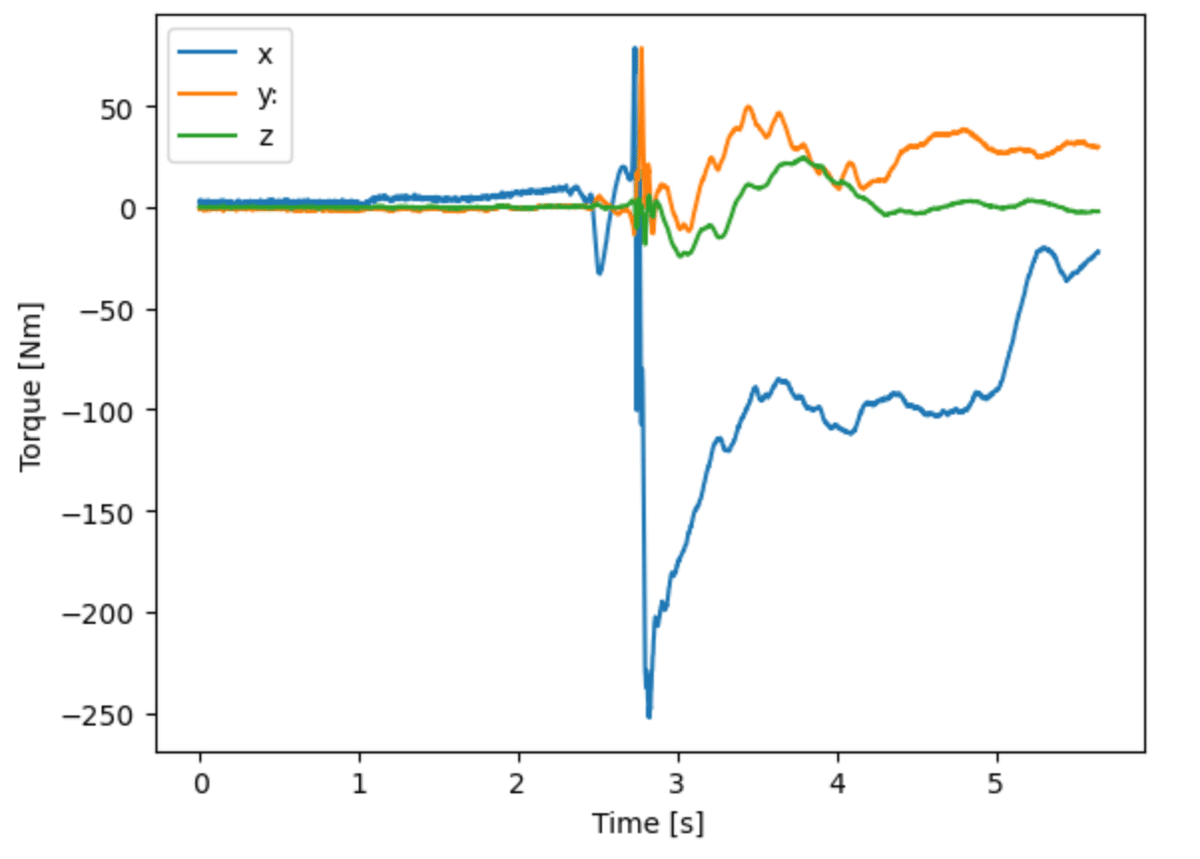
おわりに
次章
では,ここで示したコードを利用し,具体的な計算例を示していく.



【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
