
動かして学ぶバイオメカニクス #3 〜身体の慣性パラメータ〜
力学計算の基本は運動方程式.その計算には質量・慣性モーメントなどの身体の構造由来のパラメータが必要である.ここでは,ニュートンの運動方程式を解くために,特に,身体各部位の質量と重心位置を計算する方法を述べる.
おさらい
前章
では,多関節構造をPythonのclassで表現し,二分木探索(再帰呼び出し)による合成の質量を計算するプログラムを例題として取り上げた.ここで,classはデータを格納する表の役割を果たす.この表に親子関係,兄弟姉妹関係,重心位置などを格納し,今後の逆動力学計算の準備を行うことになる.
また,逆動力学計算の基本は漸化式(≒ 再帰関数)であることを前章で述べたが,この親子・兄弟姉妹関係を記述した表(class)を利用し,再帰呼び出しで複雑になりがちな力学計算自体のコードが簡潔に書くことができる.
ここでは,各部位の身体重心を計算するためのclassを別途に定義し,合成重心を計算するコードをやはり再帰で記述する.力学計算におけるこの合成重心のもつ重要な意味は,補足でその意味に少しだけふれ,おいおい理解することになる.
逆動力学計算に必要なパラメータ
運動方程式を解く
運動方程式を逆方向に解くのが逆動力学計算.ここでは,この「順逆関係」についてまとめる.

たとえば,並進の運動変化を記述するニュートンの運動方程式は
$$
m \ddot{\bm{x}}_g = \bm{F}
$$
のように記述できる.ここで,$${m}$$は物体の質量,$${\bm{x}_g}$$は物体の重心の位置ベクトル,$${\bm{F}}$$は物体に作用する総和の力である.また,$${\ddot{\bm{x}}_g}$$は$${\bm{x}_g}$$に対する二階の時間微分で,物体の重心の加速度ベクトルに相当する.
一般には,もしくは式の導入の最初には,上に示した式のように左辺に慣性力,右辺に外力を記述するのが暗黙の了解である.また,力$${\bm{F}}$$を入力,運動$${\bm{x}_g}$$を出力と考えれば,右辺の力を与えれば左の運動が定まるため,順方向は右から左となる.

順方向に運動方程式を解く際には,入力である力$${\bm{F}}$$を与え,$${\bm{x}_g}$$を定めることになるが,たとえば重力しか外力が作用しないときは,前述の式が微分方程式であるのでこれを解析的に解き,解$${\bm{x}_g}$$を得ることになる.もし,外力$${\bm{F}}$$が定数(パラメータ)や数学的関数で記述できず,解析的に解くことができない場合は,力覚センサなどで計測した値を使い,ルンゲクッタ法などを用いて数値的にシミュレーションで解を得ることになる.身体運動の問題では,恐らく後者で解くことが多くなるだろう.いずれにせよ,このような順方向の力学計算は順動力学(forward dynamics)と呼ぶ.
これとは反対に,左辺から右辺を計算するのが逆方向で,運動$${\bm{x}_g}$$を計測し,入力である力$${\bm{F}}$$を推定するのが逆動力学(inverse dynamics)である.
逆動力学は代数的な計算にとどまるが,身体各部位の質量$${m}$$と,身体の各部位の重心位置$${\bm{x}_g}$$が必要となる.
慣性パラメータ
ここでは,逆動力学としてニュートンの運動方程式を解くことを考えて,質量と重心位置の算出方法について考える.
もっとも正確な方法は,身体を切断し,質量と重心位置を計測する方法が考えられるが,残念ながら被験者の身体を切り出すことはできないので,何らかの方法で推定する必要がある.各部位の形状や身体の質量分布がおおよそ似ていることを考えれば,身長や体重でおおよそ,これらを統計的に推定できることも予想できるだろう.
こういった研究は昔から行われていて,アメリカの報告で,5人の屍体(cadaver)から,各部位の質量,重心位置,後から述べる慣性モーメントを実測し,そこから算出された統計モデルがある(文献1).このモデルは体重を与えれば,これらの3つのパラメータを推定することができる.ただし,5人の体格はかなりばらつきがあり,日本人の一般的なアスリートとはかなり異なる体型である.cadaverによる統計モデルには難しさが多いため,身体の形状を計測することで推定するモデルが多い.これらの研究については,国内外の多くの研究があり文献2,3などを参照するとよいだろう.
なお,これらの質量,重心位置,慣性モーメントは,力学計算をする上で,慣性パラメータ(inertia parameter),または動力学パラメータ(dynamic paremeter)と呼ばれる.
また,私見ではあるが,逆動力学解析に限って述べるならば,これらのパラメータの精度にはそれほど神経質にならなくても良い.モデルによっては一部の力$${\bm{F}}$$と,運動$${\bm{x}}$$の計測が必要だが,逆動力学計算での誤差がもっとも大きくなるのは$${\bm{x}}$$からの加速度$${\ddot{\bm{x}}}$$計算(計測)である.これは別途,フィルタリングで述べるが,もともとの位置$${\bm{x}}$$の精度が悪かったり,いい加減な加速度の計算を行うと,誤差が50%ぐらいになることもあるだろう.かなり注意深く加速度の計算を行う必要があり,その計算のための位置の計測に気を使うほうが重要である.また,他にも見落がしな誤差要因もある.
それらの誤差の大きさは,場合によっては簡単に慣性パラメータの誤差を飲み込んでしまう.
ただし,推定モデルは対象とする母集団に大きく依存するので,その中でも日本人の統計モデルを使用するが一つの有力な選択肢になるだろう.
詳細は文献1,2などを参照していただければと思うが,身体の形状を計測し,身体を輪切りに(スライス)した,均一な密度の楕円体の板の積み重ねで近似することで,慣性パラメータを算出するのが一般的な方法である(図1参照).

なお,こららの慣性パラメータを推定するモデルは,精度よりも,どこで部位を区切るか,または,重心点を算出する際の解剖学的特徴点の位置である.モデルの使い勝手の良し悪しともいえ,力学計算で使用するモデルとマッチしていないと面倒なことが多くなる.実際,これから紹介するモデルは,現在のモーションキャプチャで計測する標準的なマーカ位置に対応してはおらず,新しいモデルの開発が必要である.エリートアスリートの計測データを膨大に保有し,専門家の多いJSC(日本スポーツ振興センター)などで現在の事情にマッチした統計モデルの開発が,日本のスポーツ科学の発展のために望まれるところである.
日本人アスリートを対象とした慣性パラメータの統計モデル
文献1より,身体各部位の質量と重心位置に関して述べていく.

図3に,頭部と上肢の,各部位の重心位置と,質量の分配比を示した.
赤色の点は重心位置を特定するための解剖学的特徴点で,点間の内分比で重心点を示している.重心位置を示す破線の反対側に,体重に対する質量比を示した.カッコ内の数字は女性の数値である.当然,質量比の全パラメータの和は1.0となる.

図4に,体幹と下肢のモデルを示した.
内分比で与える重心位置

前述のように,重心位置は関節間の内分比で与えている.図5に示すように,各部位には,近位側(根元側)と遠位側(先端側)の両方に関節が存在するが,ここでは部位$${i}$$の関節は近位側の位置$${\bm{x}_i}$$に所属すると定義する.そこで,部位$${i}$$の遠位側に位置する関節は,子の部位$${i+1}$$に所属する関節となる.
ここで,部位$${i}$$の重心位置を指定する内分比を,関節$${\bm{x}_i}$$から見て$${r_i : (1-r_i)}$$とすると,部位$${i}$$の重心位置$${\bm{x}_{gi}}$$は
$$
\bm{x}_{gi} =(1-r_i)\bm{x}i + r_i \bm{x}_{i+1}
$$
で計算される.$${r_i \bm{x}i + (1-r_i) \bm{x}_{i+1}}$$ではないので注意されたい.
なお,ここで太字斜体で表した記号$${\bm{x}}$$はベクトルである.
合成重心
ここでは,得られた各部位の重心位置$${\bm{x}_{gi}}$$から,複数の部位(図5では,$${i-1, i, i+1}$$番目のリンク)の合成重心を考える.
重心(center of gravity)とは,各部位に作用する「重力が作り出す力のモーメントが釣り合う点」である.力のモーメントについては
を参照されたい.
2つの物体の(合成の)重心$${\bm{x}_G}$$は,図6のように2つの物体の重力が作る力のモーメントの釣り合う点,すなわち2つの重力がバランスする点で定義される.

この,各物体に作用する重力$${m_1\bm{g}, m_2 \bm{g}}$$が作り出す力のモーメント$${\bm{r}_1 \times m_1 \bm{g}}$$と$${\bm{r}_2 \times m_2 \bm{g}}$$が釣り合う点では,
$$
\bm{r}_1 \times m_1 \bm{g} + \bm{r}_2 \times m_2 \bm{g} = \bm{0}
$$
が成り立つ.ここで,$${\bm{0}}$$はすべての成分が$${0}$$であるゼロベクトル,$${\times}$$はベクトルの外積である.
外積については
を参照されたい.
である.そこで$${\bm{r}_1=\bm{x}_1-\bm{x}_G, \bm{r}_2=\bm{x}_2-\bm{x}_G}$$とすると,
$$
\bm{r}_1 \times m_1 \bm{g} + \bm{r}_2 \times m_2 \bm{g} = 0\\ (\bm{x}_1-\bm{x}_G) \times m_1 \bm{g} = -(\bm{x}_2-\bm{x}_G) \times m_2 \bm{g}\\ m_1(\bm{x}_1 \times \bm{g}) -m_1(\bm{x}_G \times \bm{g}) = - m_2(\bm{x}_2 \times \bm{g}) + m_2(\bm{x}_G \times \bm{g}) \\ m_1(\bm{x}_1 \times \bm{g}) + m_2(\bm{x}_2 \times \bm{g}) = m_1 (\bm{x}_G \times \bm{g}) + m_2 (\bm{x}_G \times \bm{g}) \\ (m_1 \bm{x}_1+m_2 \bm{x}_2) \times \bm{g} = (m_1+m_2) \bm{x}_G \times \bm{g}
$$
となるため
$$
\bm{x}_G = \frac{m_1 \bm{x}_1+m_2 \bm{x}_2}{m_1+m_2}
$$
重心$${\bm{x}_G}$$を得る.これは,2つの物体の重心間の,質量の比で記述される内分点となっている.
次に,複数の部位の合成重心を考える.

図7の各部位には重力$${m_i \bm{g}}$$が作用し,ある点$${\bm{x}_{G}}$$まわりの,この重力が作る力のモーメントは
$$
\bm{r}_i \times m_i \bm{g}
$$
となる.ここで$${\bm{r}_i}$$は,$${\bm{r}_i = \bm{x}_{gi} - \bm{x}_{G}}$$で定義され,点$${\bm{x}_{G}}$$から見た重心$${\bm{x}_{gi}}$$の位置ベクトルを意味する(青色のベクトル).
次に,これを加算し,重力が作り出す力のモーメントの和は
$$
\sum (\bm{r}_i \times m_i \bm{g})
$$
となり,$${\bm{r}_i}$$を座標系の原点から見た式に書き換えると
$$
\sum m_i \left(( \bm{x}_{gi} - \bm{x}_{G})\times \bm{g}\right)
$$
となり,これが0ベクトルとなる点,すなわち$${\bm{x}_{G}}$$まわりの力のモーメントが釣り合う場所が重心である.この式から,
$$
\sum m_i \left(( \bm{x}_{gi} - \bm{x}_{G})\times \bm{g}\right) = \bm{0} \\\sum m_i \left(\bm{x}_{gi} \times \bm{g}\right) = \sum m_i \left(\bm{x}_{G}\times \bm{g}\right)\\ \sum (m_i \bm{x}_{gi}) = \sum m_i ~\bm{x}_{G}
$$
$$
\bm{x}_{G} = \frac{\sum m_i \bm{x}_{gi}}{\sum m_i}
$$
重心$${\bm{x}_{G}}$$を得る.
重心は,質量$${m_i}$$で重みづけた各重心位置$${m_i \bm{x}_{gi}}$$の総和を,全質量$${\sum m_i}$$で割ったもので,結果的に質量中心(center of mass)と同義になる(補足1参照).
後半では,この式のそれぞれ($${\sum m_i, m_i \bm{x}_{gi}, \sum (m_i \bm{x}_{gi})}$$)に対応する関数のコード( Resultant_Mass(), WeightedJoint(), Resultant_WeightedJoint() )を示す.
以上より,各部位の重心位置を推定するためには,関節位置,または解剖学的特徴点をモーションキャプチャなどで計測(または複数マーカから推定)する必要がある.
各部位の質量と重心位置計算例
以下の計算に必要な,モーションキャプチャによって計測されたマーカの位置データは,この「リンク」からダウンロードをしていただき,下記の計算でご利用いただきたい.もし,ご自身のデータがあるならば,それを利用して計算するのもよいだろう.
計算の準備:モーションキャプチャデータの取り込み
もし,ご自身のデータを利用する場合は,この部分の計算は不要となる.
まず,以下の計算で必要なパッケージをimportする.
import pandas as pd
import numpy as nppandasはcsvやExcelデータなどを読み込む際に便利なパッケージ,numpyは行列計算に欠かせないパッケージである.特にnumpyは今後の計算で,常に必要となるだろう.
さらに,ご自身の計算環境における,ダウンロードしたファイルのパスを下記に指定し,
file_path = '/Users/…../sample_220908.csv' # Mac環境の例
file_path = 'C:\Users\...\sample_220908.csv' # Windows環境の例下記の関節データを抽出する関数を定義する.
# CSVデータからヘッダだけ抽出
def extract_df_header(file_path):
return pd.read_csv(file_path, header=None, nrows=5, index_col=1).T
# skeletonの名前を抽出
def extract_skeleton_name(file_path):
df = extract_df_header(file_path)
marker_name = df['Name'][2]
position_col = marker_name.find(':')
return marker_name[:position_col]
# ファイル名とマーカの名前を引数に与えてデータを抽出する関数
def extract_marker(file_path, marker_name):
sk_name = extract_skeleton_name(file_path) # skeleton
df_main = pd.read_csv(file_path, header=[4]) # データだけ抽出
df = extract_df_header(file_path) # headerだけ抽出
df_selected = df[df['Name']== sk_name+':'+marker_name] # ヘッダがName_Nameと一致する部分だけ抽出
selected_rows = df_selected.index # 一致する列
marker_data = np.array(df_main.iloc[:, selected_rows[-3:]].values) #後ろから3個データを取得す
return marker_dataこのコードは,csvファイルのヘッダの構造に依存し,PythonのCSVデータの抽出方法に依存するので,とりあえず内容は忘れてよい.もし勉強をするなら,PythonのPandasについては,文献5や
などを参照されたい.
この関数を利用し,例えば
extract_marker(file_path, 'LFin')のように関節名を指定すると,
array([[0.018877, 1.24577 , 1.500693],
[0.022515, 1.234573, 1.503935],
[0.026197, 1.223447, 1.507309],
[0.030223, 1.211998, 1.510461],
[0.034174, 1.200741, 1.513394],
[0.038145, 1.189193, 1.516207],
[0.042255, 1.177636, 1.518722],
[0.046591, 1.165993, 1.521309],
[0.05075 , 1.154376, 1.523558],
[0.055073, 1.142708, 1.525432],
[0.059435, 1.131087, 1.527193],
[0.063587, 1.11955 , 1.528725],
[0.067956, 1.107988, 1.530126],
[0.072341, 1.096666, 1.531303],
[0.076608, 1.085369, 1.532361],
[0.080735, 1.07421 , 1.533235],
[0.084965, 1.063325, 1.53387 ],
[0.089128, 1.0524 , 1.534399],
[0.093151, 1.041798, 1.534861],
[0.097129, 1.031392, 1.535092],
[0.101088, 1.021111, 1.535228],
[0.104985, 1.011005, 1.535252],
[0.108783, 1.001081, 1.535209],
[0.112458, 0.99143 , 1.535038],
[0.116044, 0.98198 , 1.534863],
[0.119449, 0.972778, 1.534689],
[0.122744, 0.963799, 1.534431],
[0.125946, 0.954924, 1.53428 ],
[0.129016, 0.946263, 1.533938],
[0.131918, 0.937998, 1.533656],
中略
...
...
[0.259544, 0.800529, 1.551318],
[0.260983, 0.801979, 1.550959]])のようにLFinというマーカの座標値が得られる.ご自身データをextract_marker()の代わりに,関節位置のデータを代入していただいてもよい.
これで,モーションキャプチャの出力されたCSVファイルから,関節位置のデータを抽出する準備が整った.
身体各部位の重心位置
ここでは,各部位の重心位置を計算するため(だけ)のclass BodyLink_CG を別途,準備する.インスタンス変数として,各部位の親子関係と,重心を計算するための内分比$${r}$$を格納する.
以下のコードは,提供するデータを利用して各部位の重心位置を計算するためのクラスである.したがって,ご自身で計測したモーションキャプチャなどのデータを利用し各部位の重心位置を計算する場合は,このクラスの定義も不要,または修正してご利用いただくことになる.
このクラスのメソッドとして,各リンクの親子関係を代入するset_child()関数と,各リンクの重心位置を計算するLinkCG()関数を定義した.
class BodyLink_CG:
def __init__(self, l_id:int, name, cg_ratio:float):
self.l_id = l_id # linkのID
self.name = name # linkの名前
self.cg_ratio = cg_ratio # 重心の内分比
self.child_val = None
# BodyLinkを一旦作成してから,その後に親子,兄弟姉妹関係をBodyLinkに与える.
def set_child(self, child_val):
self.child_val= child_val
# リンクの重心位置
def LinkCg(self, file_path):
div_p = self.cg_ratio # 内分比
m_name = self.name # 指定したリンクの名前
child_m_name = (self.child_val).name # その子供のリンクの名前
p = extract_marker(file_path, m_name) # そのリンクの近位側のマーカの位置データ
child_p = extract_marker(file_path, child_m_name) # 子供の(遠位側)リンクのマーカの位置データ
return (1-div_p)*p + div_p*child_p # 内分点を与える
link_struct = [0] * 21 #配列の初期化
link_struct[0]=BodyLink_CG(0, '', .0) # 0のときストップ
link_struct[1]=BodyLink_CG(1, 'Hip', (1.-.609))
link_struct[2]=BodyLink_CG(2, 'Chest', (1.-.428))
link_struct[3]=BodyLink_CG(3, 'Neck', (1.-.821))
link_struct[4]=BodyLink_CG(4, 'RUArm', .529)
link_struct[5]=BodyLink_CG(5, 'RFArm', .415)
link_struct[6]=BodyLink_CG(6, 'RHand', .891)
link_struct[7]=BodyLink_CG(7, 'LUArm', .529)
link_struct[8]=BodyLink_CG(8, 'LFArm', .415)
link_struct[9]=BodyLink_CG(9, 'LHand', .891)
link_struct[10]=BodyLink_CG(10, 'RThigh', .4750)
link_struct[11]=BodyLink_CG(11, 'RShin', .406)
link_struct[12]=BodyLink_CG(12, 'RFoot', (1.-.595))
link_struct[13]=BodyLink_CG(13, 'LThigh', .475)
link_struct[14]=BodyLink_CG(14, 'LShin', .406)
link_struct[15]=BodyLink_CG(15, 'LFoot', (1.-.595))
link_struct[16]=BodyLink_CG(16, 'RFin', .0)
link_struct[17]=BodyLink_CG(17, 'LFin', .0)
link_struct[18]=BodyLink_CG(18, 'RToe', .0)
link_struct[19]=BodyLink_CG(19, 'LToe', .0)
link_struct[20]=BodyLink_CG(20, 'Head', .0)また,末端の部位(手,足,頭)の重心位置を計算するために,手(RHand, LHand)の先のマーカーを(RFin,LFin)として,足(RFoot,LFoot)の先のマーカとして(RToe,LToe)を,頭部(Neck)の先のマーカとして,(Head)を追加している.
前章と同様に,class BodyLinkStructureのメソッドset_child()を利用して
# 親子関係の追加
link_struct[1].set_child(link_struct[2])
link_struct[2].set_child(link_struct[3])
link_struct[3].set_child(link_struct[20])
link_struct[4].set_child(link_struct[5])
link_struct[5].set_child(link_struct[6])
link_struct[6].set_child(link_struct[16])
link_struct[7].set_child(link_struct[8])
link_struct[8].set_child(link_struct[9])
link_struct[9].set_child(link_struct[17])
link_struct[10].set_child(link_struct[11])
link_struct[11].set_child(link_struct[12])
link_struct[12].set_child(link_struct[18])
link_struct[13].set_child(link_struct[14])
link_struct[14].set_child(link_struct[15])
link_struct[15].set_child(link_struct[19])のように,親子関係を代入する.
そして,LinkCg()を利用し,
link_struct[6].LinkCg(file_path)とすることで,l_id =6 の部位,すなわち,右手(RHand)の部位の重心位置が計算する.
合成の重心位置の計算
以下のクラスは,前章で取り上げたメインとなるクラスに,各部位の重心位置をインスタンス変数に加えた class BodyLinkである.
class BodyLink:
def __init__(self, l_id:int, name, mass_ratio:float):
self.l_id = l_id # linkのID
self.name = name # linkの名前
self.mass_ratio = mass_ratio # linkの質量分配比
self.child_val = None # 子供の変数
self.sister_val = None # 兄弟姉妹の変数
self.cg = None # linkの重心位置
# BodyLinkを一旦作成してから,その後に親子,兄弟姉妹関係をBodyLinkに与える.
def set_child_sister(self, child_val, sister_val):
self.child_val= child_val
self.sister_val = sister_val
# 合成の質量(全質量)の計算
# sister == 0 なら,部分解析(そのリンクの遠位側だけ計算)
# sister != 0 (例えば1)なら,全身解析(姉妹を含める)
# bw: 体重
def Resultant_Mass(self, bw, sister=0):
if self.l_id == 0:
return 0.0
elif sister == 0: # 部分(そこから遠位のみの)解析
return bw*self.mass_ratio + (self.child_val).Resultant_Mass(bw, sister)
else: # 全身解析
return (bw*self.mass_ratio +(self.child_val).Resultant_Mass(bw, sister) +
(self.sister_val).Resultant_Mass(bw, sister))
# m * cg
def WeightedJoint(self, body_weight):
return body_weight*self.mass_ratio * self.cg
# 合成の(全)WeightedJoint
# Σ m_i * cg_i
# sister == 0 なら,部分解析(そのリンクの遠位側だけ計算)
# sisute != 0 (例えば1)なら,全身解析(兄弟を含める)
def Resultant_WeightedJoint(self, body_weight, sister=0):
if self.l_id == 0:
return 0.0
elif sister== 0: # 部分(そこから遠位のみの)解析
return self.WeightedJoint(body_weight)+\
(self.child_val).Resultant_WeightedJoint(body_weight, sister) #, sister)
else: # 全身解析
return self.WeightedJoint(body_weight)+\
self.child_val.Resultant_WeightedJoint(body_weight, sister)+\
self.sister_val.Resultant_WeightedJoint(body_weight, sister)
# 合成重心
# Resultant_WeightedJoint() / Resultant_Mass()
# = Σ(m_i * cg_i) / Σ m_i
# sister == 0 なら,部分解析(そのリンクの遠位側だけ計算)
# sisute != 0 (例えば1)なら,全身解析(兄弟を含める)
def Resultant_Cg(self, body_weight, sister=0):
return self.Resultant_WeightedJoint(body_weight, sister)/self.Resultant_Mass(body_weight, sister)
b_link = [0] * 16 #配列の初期化
b_link[0]=BodyLink(0, '', .0) # 0のときストップ
b_link[1]=BodyLink(1, 'Hip', .187)
b_link[2]=BodyLink(2, 'Chest', .302)
b_link[3]=BodyLink(3, 'Head', .069)
b_link[4]=BodyLink(4, 'RUArm', .027)
b_link[5]=BodyLink(5, 'RFArm', .016)
b_link[6]=BodyLink(6, 'RHand', .006)
b_link[7]=BodyLink(7, 'LUArm', .027)
b_link[8]=BodyLink(8, 'LFArm', .016)
b_link[9]=BodyLink(9, 'LHand', .006)
b_link[10]=BodyLink(10, 'RThigh', .110)
b_link[11]=BodyLink(11, 'RShin', .051)
b_link[12]=BodyLink(12, 'RFoot', .011)
b_link[13]=BodyLink(13, 'LThigh', .110)
b_link[14]=BodyLink(14, 'LShin', .051)
b_link[15]=BodyLink(15, 'LFoot', .011)
# 親子関係と兄弟姉妹関係を下記でb_linkのchild_val, sister_valに追記
b_link[1].set_child_sister(b_link[2], b_link[0])
b_link[2].set_child_sister(b_link[3], b_link[10])
b_link[3].set_child_sister(b_link[0], b_link[4])
b_link[4].set_child_sister(b_link[5], b_link[7])
b_link[5].set_child_sister(b_link[6], b_link[0])
b_link[6].set_child_sister(b_link[0], b_link[0])
b_link[7].set_child_sister(b_link[8], b_link[0])
b_link[8].set_child_sister(b_link[9], b_link[0])
b_link[9].set_child_sister(b_link[0], b_link[0])
b_link[10].set_child_sister(b_link[11], b_link[13])
b_link[11].set_child_sister(b_link[12], b_link[0])
b_link[12].set_child_sister(b_link[0], b_link[0])
b_link[13].set_child_sister(b_link[14], b_link[0])
b_link[14].set_child_sister(b_link[15], b_link[0])
b_link[15].set_child_sister(b_link[0], b_link[0])class BodyLinkに,新たに,cgというインスタンス変数を追加し,合成重心を計算するメソッドResultant_Cg()なども加筆した.
ここで記述されている各関数(Resultant_Mass(), WeightedJoint(), Resultant_WeightedJoint(), Resultant_Cg())については,補足2を参照されたい.
なお,この計算を行う前に,インスタンス変数cgには,以下のように,前述のLinkCg()で各部位の重心位置を代入する.
b_link[4].cg = link_struct[4].LinkCg(file_path)
b_link[5].cg = link_struct[5].LinkCg(file_path)
b_link[6].cg = link_struct[6].LinkCg(file_path)ここでは,リンク4~6,すなわち右上腕(RUArm:4),右前腕(RFArm:5),右手(RHand:6)だけに重心位置を与えた.
もし,ご自身のデータをご利用になる場合は,別途,各b_link[l_id].cgに重心位置を代入されたい.
以上で合成重心を計算する準備が整い,たとえば
b_link[4].Resultant_Cg(86., sister=0)によって,リンク4,すなわちRUArm以下の全リンク(RUArm + RFArm + RHand)の合成の重心を計算し,
array([[ 4.51862958e-01, 1.33431858e+00, 5.03663627e-01],
[ 4.48375173e-01, 1.33598953e+00, 5.08199452e-01],
[ 4.44577641e-01, 1.33764518e+00, 5.12844640e-01],
[ 4.40755055e-01, 1.33932237e+00, 5.17489231e-01],
[ 4.36779185e-01, 1.34107330e+00, 5.22419164e-01],
[ 4.32541278e-01, 1.34267180e+00, 5.27152035e-01],
[ 4.28468759e-01, 1.34456732e+00, 5.32138445e-01],
[ 4.23617506e-01, 1.34610935e+00, 5.37063773e-01],
[ 4.18944130e-01, 1.34773885e+00, 5.42205537e-01],
[ 4.14328217e-01, 1.34955277e+00, 5.47547389e-01],
[ 4.09314082e-01, 1.35121599e+00, 5.52917540e-01],
[ 4.04177012e-01, 1.35287228e+00, 5.58380047e-01],
[ 3.98723245e-01, 1.35443997e+00, 5.63846872e-01],
[ 3.93258147e-01, 1.35601524e+00, 5.69538401e-01],
[ 3.87542662e-01, 1.35764915e+00, 5.75366671e-01],
[ 3.81457466e-01, 1.35906281e+00, 5.81304246e-01],
[ 3.75611416e-01, 1.36066645e+00, 5.87364996e-01],
[ 3.68886185e-01, 1.36192297e+00, 5.93517200e-01],
[ 3.61897031e-01, 1.36335899e+00, 5.99840510e-01],
:
:
[ 1.63972041e-01, 1.19255410e+00, 1.85327230e+00],
[ 1.71683353e-01, 1.18100109e+00, 1.85658213e+00]])という結果が得られる.
今回作成したクラスと関数の構造について,図8にまとめた.

先にも述べたが,2番めの「重心計算のためのクラス BodyLink_CG」は,提供するデータを利用して各部位の重心位置を計算するためのクラスであるため,もしご自身のデータを利用する場合は,このクラスの定義は不要である.
その場合,3次元の重心位置の配列データを計算し,別途,class BodyLinkのインスタンス変数cgにその重心を代入されたい.
次章
では,各リンク(部位)の関節に作用する力を,ニュートンの運動方程式を再帰的に解くことで計算する.
補足1:重心と質量中心
重心(cemter of gravity)は,重力が作り出す力のモーメントが釣り合う点である.

2個の物体の場合の重心は,2つの重力のバランスする点で表現できる(図9).物理的定義を再度示すと,
$$
\bm{r}_1 \times m_1 \bm{g} + \bm{r}_2 \times m_2 \bm{g} = 0 \\ (m_1 \bm{x}_1+m_2 \bm{x}_2) \times \bm{g} = (m_1+m_2) \bm{x}_G \times \bm{g}
$$
となり,これより,2個の場合の重心
$$
\bm{x}_G = \frac{m_1 \bm{x}_1+m_2 \bm{x}_2}{m_1+m_2}
$$
を得る.これは,$${m_1, m_2}$$の質量比による内分点で定まる.
一方,質量中心(center of mass)は,複数の物体を一つの物体と考える際の合成の運動方程式の「物体の代表点」をどこに考えればよいのか?という問題から定義できる(図10).
また,冒頭で並進のニュートン運動方程式は重心の加速度で記述すると,説明なしに述べたが,以下にその理由を説明することになる.

たとえば,2つの物体の合成の運動方程式は
$$
m_1 \ddot{\bm{x}}_1 + m_2 \ddot{\bm{x}}_2 = \bm{F}
$$
となるが,これの代表点$${\bm{x}_G}$$に関する運動方程式を考えると
$$
(m_1+m_2) \ddot{\bm{x}}_G = \bm{F}
$$
となるので,
$$
m_1 \ddot{\bm{x}}_1 + m_2 \ddot{\bm{x}}_2 = (m_1+m_2) \ddot{\bm{x}}_G
$$
が成り立つことから,代表点の加速度$${\ddot{\bm{x}}_G}$$
$$
\ddot{\bm{x}}_G = \frac{m_1 \ddot{\bm{x}}_1 + m_2 \ddot{\bm{x}}_2}{m_1+m_2}
$$
を得る.そこで代表点$${\bm{x}_G}$$についても
$$
\bm{x}_G = \frac{m_1 \bm{x}_1 + m_2 \bm{x}_2}{m_1+m_2}
$$
が成り立ち,代表点,すなわち質量中心も質量で重み付けられた重心位置となり,これは重心と同様に,$${m_1, m_2}$$の質量比による内分点となる(図11).
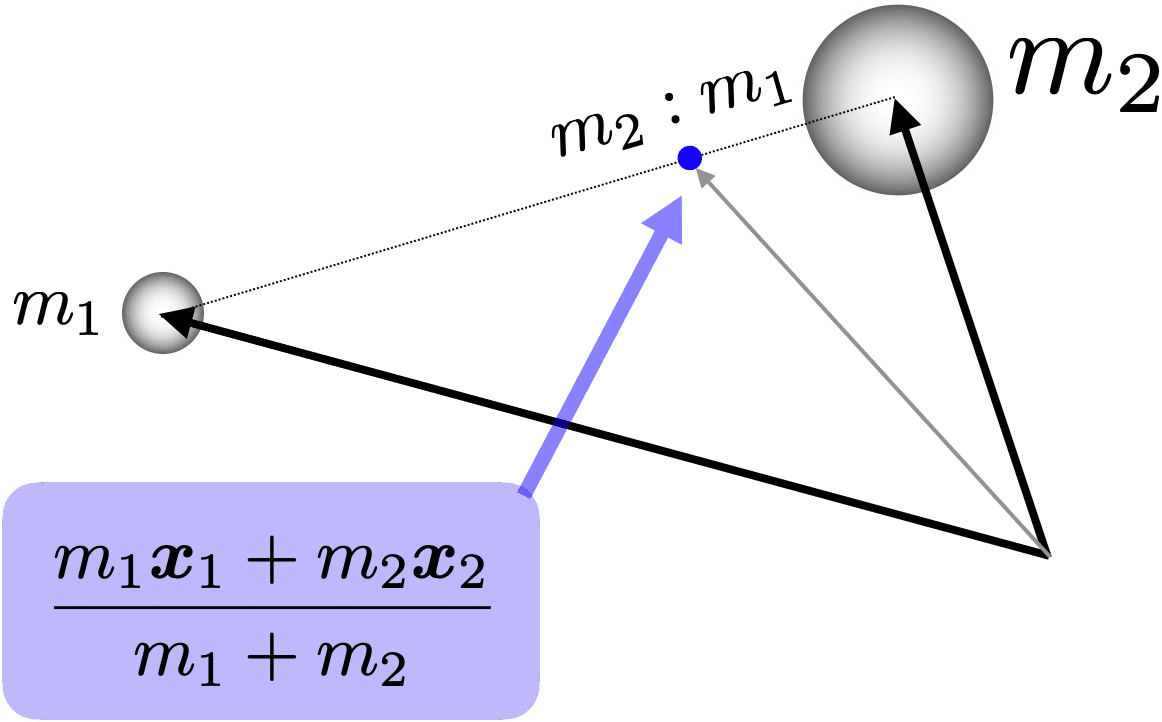
このように,2個の質点の重心と質量中心は,異なる定義であるが等価である.同様に,複数の物体(質点)の合成の重心と質量中心は
$$
\bm{x}_{G} = \frac{\sum m_i \bm{x}_{gi}}{\sum m_i}
$$
で定義されることを前に示した.
したがって運動方程式を考える際,$${\bm{x}_G}$$を質量中心と呼ぶほうが正確であるが,ここでは比較的多く使用されている重心という用語を使用する.
補足2:重心計算の関数について
重心を計算する関数を以下のように定義したが,ここでは,コードについて補足する.
# 合成の質量(全質量)の計算
# sister == 0 なら,部分解析(そのリンクの遠位側だけ計算)
# sister != 0 (例えば1)なら,全身解析(姉妹を含める)
# bw: 体重
def Resultant_Mass(self, bw, sister=0):
if self.l_id == 0:
return 0.0
elif sister == 0: # 部分(そこから遠位のみの)解析
return bw*self.mass_ratio + (self.child_val).Resultant_Mass(bw, sister)
else: # 全身解析
return (bw*self.mass_ratio +(self.child_val).Resultant_Mass(bw, sister) +
(self.sister_val).Resultant_Mass(bw, sister))
# m * cg
def WeightedJoint(self, body_weight):
return body_weight*self.mass_ratio * self.cg
# 合成の(全)WeightedJoint
# Σ m_i * cg_i
# sister == 0 なら,部分解析(そのリンクの遠位側だけ計算)
# sisute != 0 (例えば1)なら,全身解析(兄弟を含める)
def Resultant_WeightedJoint(self, body_weight, sister=0):
if self.l_id == 0:
return 0.0
elif sister== 0: # 部分(そこから遠位のみの)解析
return self.WeightedJoint(body_weight)+\
(self.child_val).Resultant_WeightedJoint(body_weight, sister) #, sister)
else: # 全身解析
return self.WeightedJoint(body_weight)+\
self.child_val.Resultant_WeightedJoint(body_weight, sister)+\
self.sister_val.Resultant_WeightedJoint(body_weight, sister)
##### 合成重心 #####
# Resultant_WeightedJoint() / Resultant_Mass()
# = Σ(m_i * cg_i) / Σ m_i
# sister == 0 なら,部分解析(そのリンクの遠位側だけ計算)
# sisute != 0 (例えば1)なら,全身解析(兄弟を含める)
def Resultant_Cg(self, body_weight, sister=0):
return self.Resultant_WeightedJoint(body_weight, sister)/self.Resultant_Mass(body_weight, sister)これまで示したように,合成重心は
$$
\bm{x}_{G} = \frac{\sum m_i \bm{x}_{gi}}{\sum m_i}
$$
で表されるが,このうちの右辺の各式は以下の関数に対応する.
$${\sum m_i}$$:Resultant_Mass()
$${m_i \bm{x}_{gi}}$$:WeightedJoint()
$${\sum m_i \bm{x}_{gi}}$$:Resultant_WeightedJoint()
また,$${\sum}$$の記号が含まれる式で,前章で示した再帰呼び出し用いられ,ここでは,関数Resultant_Mass(),Resultant_WeightedJoint()が再帰が使用している.
関数Resultant_Mass()は,$${\sum m_i}$$のように質量を加算する関数で,前章
で示した関数Resultant_Mass()と等しく,
bw*self.mass_ratio +(self.child_val).Resultant_Mass(bw, sister) +
(self.sister_val).Resultant_Mass(bw, sister)質量(bw*mass_ratio) + 自身の関数(Resultant_Mass()) を呼び出しすことで,合計の質量を計算している.
これに対して,関数Resultant_WeightedJoint()も,ほぼ同様な定義で,
self.WeightedJoint(body_weight)+
self.child_val.Resultant_WeightedJoint(body_weight, sister)+
self.sister_val.Resultant_WeightedJoint(body_weight, sister)と定義し,
WeightedJoint()+自身の関数(Resultant_WeightedJoint())
を呼び出している.
ここで,
m:各部位の質量
cg:各部位の重心位置
とすると,
WeightedJoint()は,m*cg,すなわち「質量で重み付けられた重心」である.
そこで,Resultant_WeightedJoint()は,このWeightedJoint()を加算し,重み付けされた重心の総和(Σ m_i*cg_i)を計算する関数で,前述のような再帰呼び出しで定義している(以下で,加算重心の和()関数と呼ぶ).
例えば,右上腕(RUArm, l_id=4)に対して計算を行うと,以下の図12

のような繰り返し計算を行い,結果,右手(RHand, l_id=6)まで,重みづけられた重心を加算し,加算重心の和(4) = Resultant_WeightedJoint(4)は
m(4)*cg(4) + m(5)*cg(5) + m(6)*cg(6)
を計算する.
最終的に,これらを利用し合成重心$${\bm{x}_{G}}$$は,

で定義される Resultant_Cg()で計算されている.
参考文献
1)Chandler, R. F, et al. Investigation of Inertial Properties of the Human Body, AIR FORCE AEROSPACE MEDICAL RESEARCH LAB WRIGHT-PATTERSON AFB OH, 1975.
2)阿江, 湯, 横井,日本人アスリートの身体部分慣性特性の推定,バイオメカニズム,Vol. 11, pp. 23--33, 1992
3)横井,剛体リンクモデルのため身体部分剛体特性定数,バイオメカニズム学会誌,Vol.17, No.4, pp.241--249, 1993
https://www.jstage.jst.go.jp/article/sobim/17/4/17_KJ00000971853/_pdf
4)(人工知能研究センター)人体特性文献データベース,3.身体慣性特性文献-阿江、湯、横井 1992
5)Wes McKinney 著,Pythonによるデータ分析入門 ―NumPy、pandasを使ったデータ処理,オライリージャパン,2013


【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
