IMUによるモーションセンシング #3　〜加速度信号と座標系〜

2023年10月19日 16:22

前章では加速度とは速度変化を示すグラフ上ではその速度曲線の接線の傾きであることと，それを計測する加速度センサはどちらかというと力センサとしての信号を出力するということを述べた．本章では，微分や加速度の数学的意味について復習をした上で，座標系と加速度の関係について述べる．

IMUを含むモーションセンサはウェアラブルセンサとも呼ばれ，計測は簡単だが，一方で運動学的な理解が不足すると解析で苦労する．単に加速度の大きさを知りたいという場合は簡単だが，剛体の加速度を対象とすると複雑となる．ここで，しっかりと加速度の運動学的な理解を深めていただきたい．

加速度の基礎

そもそも加速度とは？　〜数学的な視点からの復習〜

前章

でも加速度の性質を述べたが，加速度の意味について数学的な視点から復習する．

速度は位置を時間微分することで計算でき，加速度はその速度をもう１回微分することで加速度を計算することができる．ここで時間微分（＝時間で微分すること）とは曲線の接線の横軸の時間に対する傾き・勾配を求めることである．

図１に三角関数の曲線を示した．ここで述べている時間微分とは，図１左の異なる2点の縦軸と横軸（時間軸）の比（$${\frac{\delta v}{\delta t}}$$）で表される緑の実線の傾きを考え，さらにその極限，すなわち図１右のようにすなわち2点の間隔を縮めていく作業を通し，その点における接線（赤色の実線）の傾きを計算することである．

これを，速度$${\bm{v}(t)}$$と加速度$${\bm{a}(t) = \dot{\bm{v}}(t)}$$を使って数学表記するなら

$$
\begin{aligned}
\bm{v}(t) &= \dot{\bm{x}}(t) = \frac{d {\bm{x}}(t)}{dt}
\\
\bm{a}(t) &= \dot{\bm{v}}(t) = \frac{d {\bm{v}}(t)}{dt} = \ddot{\bm{x}}(t) = \frac{d^2 {\bm{x}}(t)}{dt^2}
\end{aligned}
$$

と書くことができる．加速度は速度の一階微分であり，位置の二階微分であることを，時間微分の記号（$${"~~\dot{{}}~~"}$$をドットと呼ぶ．二階微分$${"~~\ddot{{}}~~"}$$はツードットと呼ぶ）以降でも省略することは多いが，$${(t)}$$は時間$${t}$$の関数であることを示している．

これは図2の速度曲線$${\bm{v}(t)}$$のにおいても同様に，各時刻$${t}$$で接線を描き，その接線の傾き$${\frac{d\bm{v}(x)}{dt}}$$を各時刻で算出し，赤色の加速度の曲線をプロットすることに相当する．

次に物体の形を意識し，変形しない物体（剛体と呼ぶ）の加速度について考える．

剛体の加速度

ただセンサを貼り付けるだけではだめなの？

冒頭述べたように，単にセンサを取り付けた位置の加速度の大きさを知るという目的だけなら，以下の説明は不要だろう．しかし，ラケットや道具などにセンサを取り付けてる場合，取り付けるセンサの位置や向きで信号は大きく変化する．したがって多くの場合，「加速度座標系の中の加速度信号」について理解を深めないと，その信号の意味について議論できないだろう．

加速度座標系における速度（まずは速度を考える）

剛体とは変形しない（実際にはまったく変形しないということはないが，実用的には大きな変形が少ないと考えれば良い）物体を指し，形や大きさを有する物体である．すると，いままでは点だけ考えていればよかったが，「形」を考慮することにより，位置だけでなく回転が運動の自由度に加わる．特に３次元空間における回転運動は，加速度の解析を複雑にする．

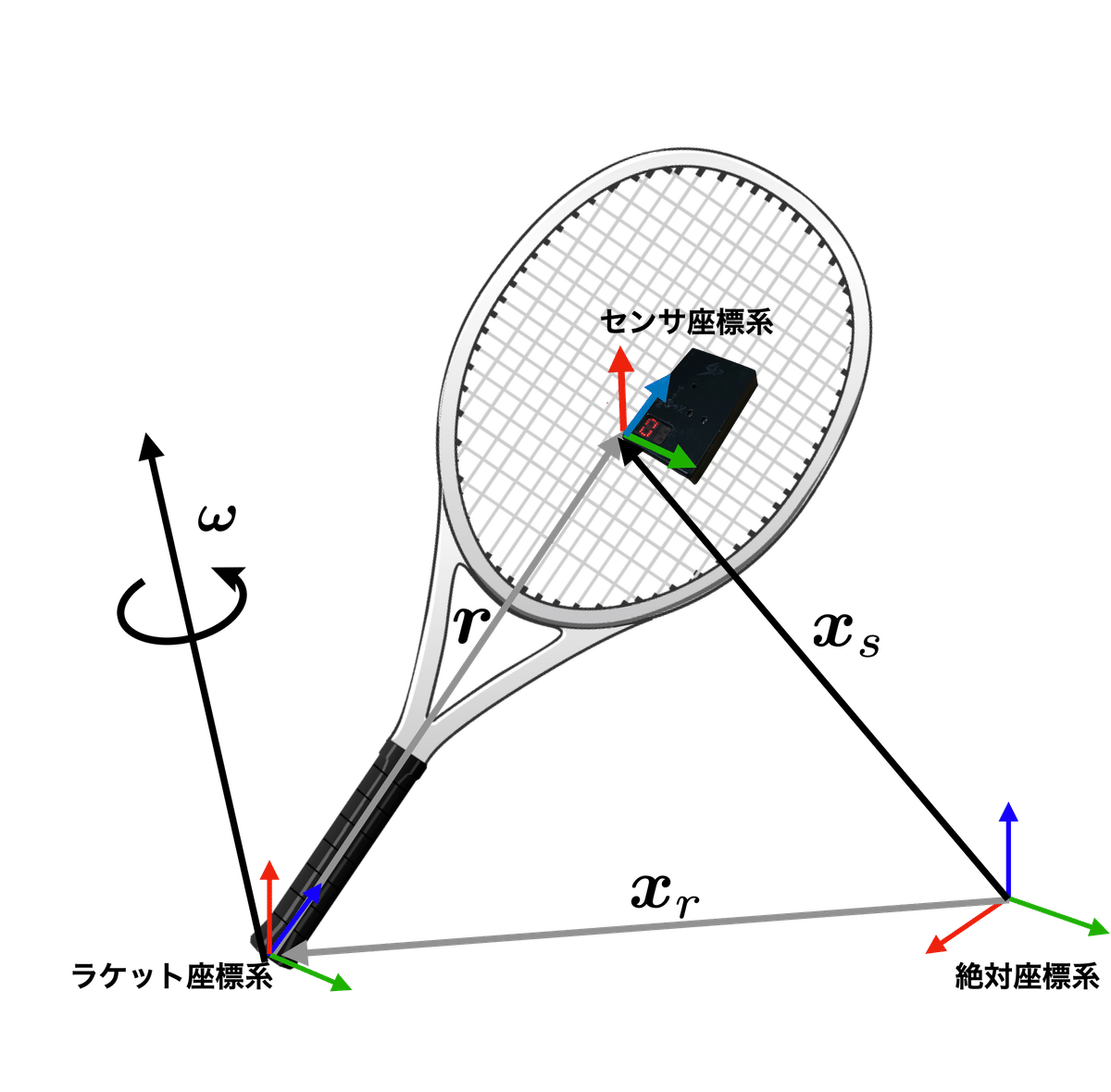
ここで，センサをテニスラケットのフェイス面中央に取り付けることを考える．このとき，地面に固定された絶対座標系，センサ座標系，ラケット座標系の３つの座標系を考える．

絶対座標系は地面に固定されていれば，自由に場所と方向を設定できる．

センサ座標系は運動する座標系だ（ここでは加速度座標系と呼んでいる）が，フェイス面中央に，センサの向きにあわせて設定されることになるので，センサ座標系の軸の方向は，センサの計測軸に合わせて定まる．

ラケット座標系も，ラケット上であれば任意に設定する加速度座標系で，ここではグリップエンドに固定することにする．ここでは，ラケット座標系とセンサ座標系は平行移動しただけの関係にあり，同じ方向を向くとする．

ここで，絶対座標系の原点から見たセンサの位置を$${\bm{x}_s}$$とする．

また，ラケット座標系を経由したセンサの位置は，

$$
\bm{x}_s = \bm{x}_r + \bm{r}
$$

のように記述することができる．ここで，$${\bm{x}_r}$$は絶対座標系の原点からみたラケット座標系の原点の位置ベクトルで，絶対座標系の原点から見たラケット座標系の原点の並進運動を示している．$${\bm{r}}$$はラケット座標系の原点から見たセンサの位置ベクトルで，ラケットは変形しないので$${\bm{r}}$$の長さ$${| \bm{r} |}$$は変化せず一定である．

次に，この式を微分することで，

$$
\begin{aligned}
\dot{\bm{x}}_s &= \dot{\bm{x}}_r + \dot{\bm{r}}
\\
&= \dot{\bm{x}}_r + \bm{\omega} \times \bm{r}
\end{aligned}
$$

センサ座標系の原点$${\bm{x}_s}$$の速度ベクトルを得る．ここで，$${\dot{\bm{x}}_r}$$はラケット座標系の原点の並進運動の速度ベクトルである．また，センサ座標系から見るとセンサの位置は距離が変わらないため，その速度$${\dot{\bm{r}}}$$は回転運動だけで記述でき，$${\dot{\bm{r}} = \bm{\omega} \times \bm{r} }$$と書くことができる．$${\times}$$はベクトルの外積で，このベクトルの外積は以下のように，行列とベクトルの積で記述することができる．ベクトルの外積については

や

を参照されたい．

図４に示すように，ベクトル$${\bm{r}}$$の速度$${\dot{\bm{r}} = \bm{\omega} \times \bm{r}}$$は，ラケットの角速度ベクトル$${\bm{\omega}}$$やベクトル$${\bm{r}}$$に対して直角方向を向き，ベクトル$${\bm{r}}$$の回転が作る円の接線方向を向く．

また，この速度$${\dot{\bm{r}} = \bm{\omega} \times \bm{r} }$$の外積の計算を成分で記述すると，

$$
\begin{aligned}
\dot{\bm{r}} &= \bm{\omega} \times \bm{r}
\\
\begin{bmatrix}v_x\\v_y\\v_z\end{bmatrix}
&=
\begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x\\ -\omega_y & \omega_x & 0 \end{bmatrix}
\begin{bmatrix}r_x\\r_y\\r_z\end{bmatrix}
\end{aligned}
$$

のように歪対称行列（交代行列）とベクトルの積で，記述することができる．

ここで，歪対称行列とは

$$
\begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x\\ -a_y &a_x & 0 \end{bmatrix}
$$

のように対角成分が0で，転置に対して反対称性を持つ行列である．

ここで，ベクトル$${\bm{r}}$$をラケット座標系で記述し，$${\bm{r}}$$の$${z}$$軸方向に長さ$${r}$$の距離にセンサが固定されているとすると，

$$
\bm{r} = \begin{bmatrix}0\\0\\r\end{bmatrix}
$$

と書けるので，先程の式は

と書くことができる．ラケットの固定された$${z}$$軸方向には速度は持たず，それに垂直な接線方向にだけ速度を持つことになる（図４参照）．

加速度座標系における加速度（もう１回微分をする）

次に，センサの位置ベクトル$${\bm{x}_s}$$を微分した速度ベクトルをもう１度微分し，その加速度ベクトル$${\ddot{\bm{x}}_s}$$を計算すると，

$$
\begin{aligned}
\ddot{\bm{x}}_s &= \ddot{\bm{x}}_r + \ddot{\bm{r}}
\\
&= \ddot{\bm{x}}_r + \dot{\bm{\omega}} \times \bm{r} + \bm{\omega} \times (\bm{\omega} \times \bm{r})
\end{aligned}
$$

のようになる．ここで，第１項の$${\ddot{\bm{x}}_r}$$はセンサ座標系の並進移動による加速度で，並進加速度などと呼ばれる．

第２項の$${\dot{\bm{\omega}}}$$は角加速度ベクトルで，$${\dot{\bm{\omega}} \times \bm{r}}$$は接線加速度などと呼ばれ，先程と同様に，ラケット座標系の成分で記述すると

$$
\begin{aligned}
\dot{\bm{\omega}} \times \bm{r}
&=
\begin{bmatrix} 0 & -\dot{\omega}_z & \dot{\omega}_y \\ \omega_z & 0 & -\dot{\omega}_x\\ -\dot{\omega}_y & \dot{\omega}_x & 0 \end{bmatrix}
\begin{bmatrix}0\\0\\r\end{bmatrix}
\\
&= r \begin{bmatrix} \dot{\omega}_y \\ -\dot{\omega}_x \\ 0\end{bmatrix}
\end{aligned}
$$

となり，図４の$${\bm{\omega} \times \bm{r}}$$と見比べてほしいが，それと同じ方向の接線方向で，$${z}$$軸方向に垂直な方向を向き，

第３項の$${\bm{\omega} \times (\bm{\omega} \times \bm{r})}$$は

$$
\begin{aligned}
\bm{\omega} \times (\bm{\omega} \times \bm{r})
&=
\begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x\\ -\omega_y & \omega_x & 0 \end{bmatrix}
\begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x\\ -\omega_y & \omega_x & 0 \end{bmatrix}
\begin{bmatrix}0\\0\\r\end{bmatrix}
\\
&=r \begin{bmatrix}\omega_z \omega_x \\ \omega_y \omega_z \\ -(\omega_x^2 + \omega_y^2)\end{bmatrix}
\end{aligned}
$$

となる．

ここで，この$${\bm{\omega} \times (\bm{\omega} \times \bm{r})}$$の$${z}$$成分$${-r (\omega_x^2 + \omega_y^2)}$$を，向心加速度（centripetal acceleration）と呼ぶ．この向心加速度の向きは内側で，遠心加速度の反対で，回転の中心方向を向くことに注意されたい．センサが計測する加速度も，物体に作用する力も遠心加速度や遠心力ではなく，その反対の向心加速度，向心力である．

一方，$${z}$$軸まわりの回転$${\omega_z}$$を含む際に，$${x, y}$$方向にも加速度が発生する．たとえば，ラケットの長軸を$${z}$$軸とし，その長軸まわりの回転も含めてラケットが回転する場合，長軸方向の向心加速度だけでなく，それに垂直な方向のフェイス面やその法線方向にも加速度が作用する．

これら$${\bm{\omega} \times (\bm{\omega} \times \bm{r})}$$の3成分ををまとめて向心加速度と呼ぶこともある．

ちなみに，外積を使用して記述する際には$${\bm{\omega} \times (\bm{\omega} \times \bm{r})}$$のように括弧が含まれ，この部分を先に計算する必要があるが，歪対称行列を使って記述すると，前述のように括弧を取り除くことができる．つまり，積の順番に依存しない．簡単な計算なのでご自身で確かめるとよいだろう．

さて，ラケットの角速度$${\omega}$$や角加速度$${\dot{\omega}}$$はセンサをどこに配置しても，センサが同じ方向を向いている限り同じ値を示す．つまり同じ剛体であるならば，角速度ベクトルは場所に依存しない物理量である．しかし，明らかにこれらの式はセンサ座標系の原点の位置に依存して$${\bm{r} = [r_x~r_y~r_z]^T}$$が変化する．つまり座標系に依存する．しかし，人が恣意的に与えるセンサ座標系の原点の位置が変わることで，センサの信号の大きさが変化することはないので，これは

$$
\begin{aligned}
\ddot{\bm{x}}_s &= \ddot{\bm{x}}_r + \ddot{\bm{r}}
\\
&= \ddot{\bm{x}}_r + \dot{\bm{\omega}} \times \bm{r} + \bm{\omega} \times (\bm{\omega} \times \bm{r})
\end{aligned}
$$

の式の，$${\ddot{\bm{x}}_r}$$と$${\bm{r}}$$の割合が変化することで，見かけ上，調整されていることを意味する．

センサの加速度は絶対座標系から眺めれば，単に

$$
\ddot{\bm{x}}_s
$$

と書けるが，ラケット座標系から眺めれば，

$$
\begin{aligned}
\ddot{\bm{x}}_r + \dot{\bm{\omega}} \times \bm{r} + \bm{\omega} \times (\bm{\omega} \times \bm{r})
\end{aligned}
$$

と書くことができ，このことから，総和の加速度自体は変化せずとも，解析上，座標系の設定の仕方で，見方が変化してしまうということに注意をされたい．

絶対座標系の取り方による違い

位置は異なる座標系から見れば当然異なるが，速度や加速度は絶対座標系の取り方に依存しない．

図６に示した絶対座標系Aから見たセンサの加速度は先ほど示したように，

$$
\begin{aligned}
\ddot{\bm{x}}_{sA} &= \ddot{\bm{x}}_{rA}(t) + \dot{\bm{\omega}} \times \bm{r} + \bm{\omega} \times (\bm{\omega} \times \bm{r})
\end{aligned}
$$

のように記述できる．ここで，$${\bm{x}_{rA}}$$は絶対座標系の原点から見たラケット座標系の原点の位置ベクトルで，この加速度は並進加速度である．

一方，絶対座標系Bから見たセンサの加速度は，図６に示したように，絶対座標系Aを介して

$$
\begin{aligned}
\ddot{\bm{x}}_{sB} &= \ddot{\bm{r}}_{BA} + \ddot{\bm{x}}_{rA}(t) + \dot{\bm{\omega}} \times \bm{r} + \bm{\omega} \times (\bm{\omega} \times \bm{r})
\end{aligned}
$$

と書けるが，絶対座標系Bから見たAの位置ベクトルは動かないので，$${\ddot{\bm{r}}_{BA} = \bm{0}}$$なので，結局

$$
\ddot{\bm{x}}_{sA} = \ddot{\bm{x}}_{sB}
$$

のように，$${\bm{x}_s}$$の加速度$${\ddot{\bm{x}}_s}$$は，どの動かない座標系からみても，同じである．当たり前だが，式の上で説明を行った．

剛体上の任意の位置の加速度の推定

このような性質を利用して，同じ剛体上の任意の位置の加速度を推定することを考える．具体的には，センサのない図５の水色の点の加速度を推定する．

先程，ラケット座標系からセンサの位置と，その二階微分の加速度を記述したが，今度は，センサ座標系からラケット上の任意の位置$${\bm{x}_a}$$の加速度を記述すると，

$$
\begin{aligned}
\ddot{\bm{x}}_a &= \ddot{\bm{x}}_s + \dot{\bm{\omega}} \times \bm{l}+ \bm{\omega} \times (\bm{\omega} \times \bm{l})
\\
\bm{l} &= \bm{x}_a - \bm{x}_s
\end{aligned}
$$

のように記述できる．ここで$${\bm{l}}$$はセンサ座標系から見た$${\bm{x}_a}$$の位置ベクトルである．モーションセンサ（IMU）のジャイロセンサを利用すれば，角速度ベクトル$${\bm{\omega}}$$も計測でき，センサからの位置$${\bm{l}}$$がわかれば，任意の位置の加速度を推定できる．ただし，その加速度はセンサ座標系の情報である．もし絶対座標系に変換するには，ジャイロセンサから計測される$${\bm{\omega}}$$から推定される姿勢角度行列$${ \bm{R}}$$が必要である．これについては，別途述べることとする．

ここで，座標系を明示して表示すると

$$
\begin{aligned}
{}^s \ddot{\bm{x}}_a &= {}^s \bm{R}_g {}^g\ddot{\bm{x}}_s + \dot{\bm{\omega}} \times \bm{l}+ \bm{\omega} \times (\bm{\omega} \times \bm{l})
\end{aligned}
$$

と書くことができる．ここで，記号の左肩の上付き文字は座標系を示しており，$${{}^s \ddot{\bm{x}}_a}$$はセンサ座標系で表した加速度，$${{}^g\ddot{\bm{x}}_s}$$は絶対座標系で記述された加速度を示し，$${{}^s \bm{R}_g}$$は絶対座標系からセンサ座標系への座標変換を示す．

おわりに

IMUによって計測される加速度信号には，並進加速度，向心加速度，接線加速度など，いろいろな種類加速度が含まれると考えるよりも，観察する人が与える座標系の設定の仕方で，それらの割合がかわると考えるのが良い．座標系の設定の仕方で信号の大きさが変化することは，もちろんない．

前章で述べたように，加速度センサは力センサで重力加速度を含むことを述べた．この章では一旦その事を忘れて，純粋に運動する物体の加速度だけを考えた．実際に加速度センサに計測される加速度については，別途，別の章で述べることとする．

並進運動と回転運動が混在する加速度信号の処理では，回転を考慮すべきで座標変換も行う必要があり，加速度センサだけでは処理が完結せずジャイロセンサから計測される角速度信号の助けも必要となる．この座標変換についても，別途述べることとする．

このようにウェアラブルなセンサは計測は，比較的容易だが，これらの基礎概念を理解する必要があり，面倒な一面もある．今後，理解を深めるためにモーションキャプチャのデータとの対比なども行っていく予定である．

スポーツセンシング　公式note

【著作権・転載・免責について】

権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは，スポーツセンシング社の著作物であり，スポーツセンシング社に知的所有権がありますが，自由にご利用いただいて構いません．

本ページに掲載されている記事，ソフトウェア，プログラムなどに関する著作権および工業所有権については，株式会社スポーツセンシングに帰属するものです．非営利目的で行う研究用途に限り，無償での使用を許可します．

転載
本ページの内容の転載については非営利目的に限り，本ページの引用であることを明記したうえで，自由に行えるものとします．

免責
本ページで掲載されている内容は，特定の条件下についての内容である場合があります．ソフトウェアやプログラム等，本ページの内容を参照して研究などを行う場合には，その点を十分に踏まえた上で，自己責任でご利用ください．また，本ページの掲載内容によって生じた一切の損害については，株式会社スポーツセンシングおよび著者はその責を負わないものとします．

【解析・受託開発について】

スポーツセンシングでは，豊富な知見を持つ，研究者や各種エンジニアが研究・開発のお手伝いをしております．研究・開発でお困りの方は，ぜひスポーツセンシングにご相談ください．
【例】
　・データ解析の代行
　・受託開発
　　（ハードウェア、組込みソフトウェア、PC/モバイルアプリ）
　・測定システム構築に関するコンサルティング　など
その他，幅広い分野をカバーしておりますので，まずはお気軽にお問い合わせください．

【データの計測について】

スポーツセンシング社のスタジオで，フォースプレートやモーションキャプチャを利用した計測も行えます．出力されるデータと，ここで示したプログラム（入力データの取り込み関数を少々改変する必要があるが）で，同様な解析を行えますので，まずはお気軽にお問い合わせください．

IMUによるモーションセンシング #3 〜加速度信号と座標系〜