
動かして学ぶバイオメカニクス #31 〜ヤコビ行列#5
ここでは静力学から動力学への拡張を行い,モーションキャプチャやIMUを用いた身体運動の解析に適した多体系の運動方程式を導出する.途中の導出を読み飛ばして,最後の結論だけ確認いただいても構わない.
この結論は,あたりまえだが第14章で導いた合成の運動方程式と一致することになるが,ここで述べるヤコビ行列で整理することで,より直感的かつシステマティックに合成の運動方程式を導出することを可能とする.高自由度の多関節系の運動方程式を単に合成することで導出するのはつらいが,本章での述べる方法を用いていけば可能だ.このような形式は運動方程式を線形な式とすることで,代数的に扱えることも利点としてあげられる.つまり関節に作用するトルクの物理的意味を考えやすくなり,トルクを大小だけの単なる数値として考えるのではなく,関節に作用するトルクの身体運動における意味を考える起点となる.
この方法によって導出される関節に作用するトルクは,回転の慣性力を除いて,外力と慣性力に関して全て「その関節まわりの力のモーメント」の和として計算される.これにより,その物理的・幾何学的な意味が直感的に理解できるはずだ.
はじめに
単に数値的に関節に作用するトルクを計算するためなら,漸化的ニュートン・オイラー法で効率よく計算を行うのがよいだろう.しかし,身体運動における関節に作用するトルクの物理的意味を問うことが目的なら,ここで扱う式自体が役に立つかもしれない.

これまで述べてきたように,ヤコビ行列は「微分運動学」における手先速度と関節速度を関係づける行列として導入され,幾何学的には接線速度(tangent velocity)の意味を持つ.ここまで,これを「仮想仕事の原理」を用いて「静力学」に拡張したが,さらに本章で「ダランベールの原理」を用いて「動力学」に拡張することで,力学方程式は力やトルクの関係をすべてヤコビ行列で記述される.そしてヤコビ行列は力学ではてことしての幾何学的意味を持ち(図1参照),「関節と,(慣性力を含む)力を結ぶベクトル」がわかればよいだけとなる.これは力学計算にとって,スポーツにおけるフォームや,身体運動における姿勢のもつ意味や役割を明確にする.なお,この力のモーメント$${\bm{r} \times \bm{f}}$$は,$${\bm{\tau}}$$に対して釣り合う回転力で,符号が負であることに注意されたい.
このことからも,ヤコビ行列は身体運動におけるフォームや姿勢の意味を抽象的に考える道具となることがわかるだろう.速度や加速度などの微分する世界で考えれば,もはや三角関数や角度などを使用する必要はない.座標系の原点をどこに置くかも関係ない(ただし数値的な精度では違いが生じる).身体運動の物理的意味を考える視点を運動学から力学に切り替えれば,数学的にも扱いやすいし,運動の本質を考える上でずっと合理的だ.
本章では,まずダランベールの原理を導入し,静力学から動力学への拡張を行う.
なお,次にも述べるが,動力学の計算で必要とされる,慣性項である$${m \ddot{\bm{x}}}$$や$${\bm{I} \dot{\bm{\omega}} + \bm{\omega} \times \bm{I} \bm{\omega}}$$をも一種の「力」とみなしてしまえば,これまで議論してきた静力学の枠組みの中で同じように議論ができる.これをダランベールの原理(d'Alembert's principle)と呼ぶ.
また,その結果を利用すれば,関節に作用するトルクはその関節まわりの外力と慣性力の力のモーメントの和で計算すれば良く,関節とそれらの力が作用する位置との力のモーメントであって,他の途中の関節の位置や姿勢とは無関係となる.このことは非常に便利だ.
なお,この結果は最後にまとめているので,導出を確認するのがつらい方は,最後の結果まで,読み飛ばしていただいて構わない.この結果が第14章で述べた結果と一致することを確認していただけたらと思う.
ダランベールの原理と力学計算
たとえば,以下のような運動方程式
$$
m \ddot{\bm{x}} = \bm{f}_1 + \bm{f}_2 + m \bm{g}
$$
のように,通常,運動方程式の左辺に運動量ベクトル$${\bm{p}}$$の時間微分
$$
\begin{aligned}
\bm{p} &\equiv m \frac{d \bm{x}}{dt} = m \dot{\bm{x}}
\\
\dot{\bm{p}} &= m \frac{d^2 \bm{x}}{dt^2} = m \ddot{\bm{x}}
\end{aligned}
$$
を配置し,右辺に外力を書き並べる.このことは左辺は力に相当することを意味する.そこで,左辺も一種の力とみなし,これを慣性力(inertial force)と呼んでいる.慣性力も外力もわけへだてなく力とみなしてしまうことを,ダランベールの原理(d'Alembert's principle)という.
ただし,運動方程式のスタートはやはり慣性力を左辺に,右辺に記述するのが基本である.運動方程式を最初に記述する場合は,このルールをできるだけ無視しないようするのが暗黙の了解である.また,それを無視すると誤った符号を与えることになるので注意されたい.
外力は対象とする物体に作用する力である.たとえば床反力(地面反力)を計測し,身体側の運動方程式の外力は「身体に作用する力」である.フォースプレートが計測する地面反力が下向きなら,それは反作用の「フォースプレートに作用する力」として定義されている.身体の運動方程式にとっては符号が反対である.外力の定義には注意をされたい.
この他,回転の運動方程式における慣性力として$${\mathcal{M} \equiv \bm{I} \ddot{\bm{\omega}} + \bm{\omega} \times \bm{I} \bm{\omega}}$$も慣性力として考える.
このようにダランベールの原理は特別なことを述べているわけではなく,「慣性力も力とみなす」と,単純なことを述べているだけだ.
仮想仕事の原理とダランベールの原理からの導出
1リンク機構の運動方程式:
これまで仮想仕事の原理を用いて多体系の静力学を導入したが,ダランベールの原理にしたがい,慣性力も含めて仮想仕事に原理に当てはめることを考える.
ここではまず,図2に示す球関節を有する1リンクの3次元空間での運動を考える.

この部位の球関節,重心,手先(エンドエフェクタ)の位置ベクトルをそれぞれ,$${\bm{p}_1, \bm{p}_{g1}, \bm{x}}$$とし,この部位が角速度ベクトル$${\bm{\omega}_1}$$で運動すると,手先部分の速度は
$$
\begin{aligned}
\dot{\bm{x}} &= \bm{\omega}_1 \times (\bm{x} - \bm{p}_1) = -(\bm{x} - \bm{p}_1) \times \bm{\omega}_1
\\
\dot{\bm{p}}_{g1} &= \bm{\omega}_1 \times (\bm{p}_{g1} - \bm{p}_1) = -(\bm{p}_{g1} - \bm{p}_1) \times \bm{\omega}_1
\end{aligned}
$$
となり,手先速度$${\dot{\bm{x}}}$$と重心位置$${\bm{p}_{g1}}$$の関節速度$${\bm{\omega}_1}$$に関するヤコビ行列は,
$$
\begin{aligned}
\bm{J}_x &= \frac{\partial \dot{\bm{x}}}{\partial \bm{\omega}_1} = -[( \bm{x} - \bm{p}_1) \times]
\\
\bm{J}_{g1} &= \frac{\partial \dot{\bm{p}}_{g1}}{\partial \bm{\omega}_1} = -[(\bm{p}_{g1} - \bm{p}_1) \times ]
\end{aligned}
$$
となる.この導出は,前章までの議論を参照していただきたい.
ここで,この部位の質量と慣性テンソルを$${m_1, \bm{I}_1}$$,重力加速度ベクトルを$${\bm{g}}$$,関節に作用するトルクを$${\bm{\tau}_1}$$とすると,この系に作用する外力としての力とトルクは$${m_1\bm{g}, \bm{\tau}_1}$$となる.
一方,並進の慣性力は$${m_1 \ddot{\bm{p}_{g1}}}$$,回転の慣性力は$${\mathcal{M}_1 = \bm{I} _1 \dot{\bm{\omega}_1} + \bm{\omega}_1 \times \bm{I}_1 \bm{\omega}_1}$$である.
そこで,この部位に作用する釣り合いうトルクとして,$${\bm{\tau}_1, (\bm{x} - \bm{p}_{g1}) \times (m_1\bm{g})}$$の外力以外に,ダランベールの原理から慣性力の$${\mathcal{M}_1, (\bm{p}_{g1} - \bm{p}_1) \times (m_1 \ddot{\bm{p}}_{g1})}$$も一種の力とみなせば,これらの慣性力も仮想仕事の原理の対象となる.
また,$${\bm{\omega}_1, \bm{p}_{g1}, \bm{p}_{g1}}$$に対応する仮想変位を$${\delta\bm{q}_1, \delta\bm{p}_{g1}, \delta\bm{x}}$$とすると,仮想仕事の原理から,
$$
\mathcal{M}_1^T \delta \bm{q}_1 + (m_1 \ddot{\bm{p}}_{g1})^T \delta \bm{p}_{g1} = \bm{\tau}_1^T \delta \bm{q}_1 + (m_1 \bm{g})^T \delta \bm{p}_{g1} + \bm{f}^T \delta \bm{x}
$$
が成り立つ.これは慣性力を含む各力ベクトルと,対応する仮想変位ベクトルとの内積を計算している.
ここで,
$$
\begin{aligned}
\delta \bm{p}_{g1} &= \frac{\partial \bm{p}_{g1}}{\partial \bm{q}_1} \delta \bm{q}_1
\\
\delta \bm{x} &= \frac{\partial \bm{x}}{\partial \bm{q}_1} \delta \bm{q}_1
\end{aligned}
$$
を利用し,以下のように整理すると
$$
\begin{aligned}
\left(\mathcal{M}_1^T + (m_1 \ddot{\bm{p}}_{g1})^T \frac{\partial \bm{p}_{g1}}{\partial \bm{q}_1} \right) \delta \bm{q}_1 &=
\left(\bm{\tau}_1^T + (m_1 \bm{g})^T \frac{\partial \bm{p}_{g1}}{\partial \bm{q}_1} + \bm{f}^T \frac{\partial \bm{x}}{\partial \bm{q}_1} \right) \delta \bm{q}_1
\\
\mathcal{M}_1^T + (m_1 \ddot{\bm{p}}_{g1})^T \frac{\partial \bm{p}_{g1}}{\partial \bm{q}_1} &= \bm{\tau}_1^T + (m_1 \bm{g})^T \frac{\partial \bm{p}_{g1}}{\partial \bm{q}_1} + \bm{f}^T \frac{\partial \bm{x}}{\partial \bm{q}_1}
\\
\mathcal{M}_1 + \left(\frac{\partial \bm{p}_{g1}}{\partial \bm{q}_1}\right)^T (m_1 \ddot{\bm{p}}_{g1} - m_1 \bm{g}) &= \bm{\tau}_1 + \left(\frac{\partial \bm{x}}{\partial \bm{q}_1}\right)^T \bm{f}
\\
\mathcal{M}_1 + \bm{J}_{g1}^T (m_1 \ddot{\bm{p}}_{g1} - m_1 \bm{g}) &= \bm{\tau}_1 + \bm{J}_x^T \bm{f}
\end{aligned}
$$
を得る.2行目から3行めにかけては各項を転置している.ここで,ヤコビ行列を
$$
\begin{aligned}
\bm{J}_x &= \frac{\partial \bm{x}}{\partial \bm{q}_1}% = \frac{d \dot{\bm{x}}}{d \bm{\omega}_1} = -[( \bm{x} - \bm{p}_1) \times] = -[\bm{p}^1_{x} \times]
\\
\bm{J}_{g1} &= \frac{\partial \bm{p}_{g1}}{\partial \bm{q}_1}% = \frac{d \dot{\bm{p}}_{g1}}{d \bm{\omega}_1} = -[( \bm{p}_{g1} - \bm{p}_1) \times] = -[\bm{p}^1_{g1} \times]
\end{aligned}
$$
としている.さらに,これを$${\bm{\tau}_1}$$について整理すれば,
$$
\begin{aligned}
%\bm{\tau}_1 &= \mathcal{M}_1 + \bm{J}_{g1}^T (m_1 \ddot{\bm{p}_{g1}}) - %\bm{J}_{g1}^T (m_1 \bm{g}) - \bm{J}_x^T \bm{f}
%\\
\bm{\tau}_1 &= \mathcal{M}_1 + \bm{J}_{g1}^T(m_1 \ddot{\bm{p}_{g1}} - m_1 \bm{g}) - \bm{J}_x^T \bm{f}
\\
&= \mathcal{M}_1 + \bm{J}_{g1}^T \mathcal{F}_1 - \bm{J}_x^T \bm{f}
%\\
%&= \mathcal{M}_1 - [( \bm{p}_{g1} - \bm{p}_1) \times]^T \mathcal{F} - (-[( \bm{x} - \bm{p}_1) \times]^T) \bm{f}
%\\
%&= \mathcal{M}_1 + [( \bm{p}_{g1} - \bm{p}_1) \times] \mathcal{F}_1 - [( %\bm{x} - \bm{p}_1) \times] \bm{f}
\end{aligned}
$$
となる.ここで,$${\mathcal{F}_1 \equiv m_1 (\ddot{\bm{p}_{g1}} - \bm{g})}$$とし,各部位の重心に作用する力として,慣性力と重力をひとつにまとめている.
次に,ヤコビ行列を具体的に
$$
\begin{aligned}
\bm{J}_x &= \frac{\partial \bm{x}}{\partial \bm{q}_1} = \frac{\partial \dot{\bm{x}}}{\partial \bm{\omega}_1} = -[( \bm{x} - \bm{p}_1) \times] = -[\bm{r}_1^{x} \times]
\\
\bm{J}_{g1} &= \frac{\partial \bm{p}_{g1}}{\partial \bm{q}_1} = \frac{\partial \dot{\bm{p}}_{g1}}{\partial \bm{\omega}_1} = -[( \bm{p}_{g1} - \bm{p}_1) \times] = -[\bm{r}_1^{g1} \times]
\\
\bm{r}_1^x &\equiv \bm{x} - \bm{p}_1\\
\bm{r}_1^{g1} &\equiv \bm{p}_{g1} - \bm{p}_1
\end{aligned}
$$
のように求めた(図3参照).ここで,$${\bm{r}_a^b}$$は$${a}$$から$${b}$$への位置ベクトルを意味する(図3では緑色の矢印に相当).
そこで,先程の式にこれを代入すると,

$$
\begin{aligned}
\bm{\tau}_1 &= \mathcal{M}_1 + \bm{J}_{g1} \mathcal{F}_1 -\bm{J}_{x} \bm{f}
\\
&= \mathcal{M}_1 + [( \bm{p}_{g1} - \bm{p}_1) \times] \mathcal{F}_1 - [( \bm{x} - \bm{p}_1) \times] \bm{f}
\\
&= \mathcal{M}_1 + [\bm{r}_1^{g1} \times] \mathcal{F}_1 - [\bm{r}_1^x \times] \bm{f}
\\
&= \left(\bm{I} _1 \dot{\bm{\omega}_1} + \bm{\omega}_1 \times \bm{I}_1 \bm{\omega}_1 \right) + m_1[\bm{r}_1^{g1} \times] (\ddot{\bm{p}}_1 - \bm{g})- [\bm{r}_1^x \times] \bm{f}
\end{aligned}
$$
を得る(図3参照).
トルク$${\bm{\tau}_1}$$は,すべての外力と慣性力に対する,「$${\bm{p}_1}$$まわり」の力のモーメントの和で記述されている.
この結果は,普通に重心まわりのオイラーの運動方程式と解いた場合と一致するが,ここでは示さず,次に示す2リンク機構で確認する.可能なら読者はチャレンジしてみていただきたい.
ヒント:まず,オイラーの回転の運動方程式と,ニュートンの並進運動方程式をたてる.その際,ここで示した導出方法では不要なので表れていない.根本の関節の$${\bm{p}_1}$$に作用する力を考慮する.その力を消去すればよいだけだ.
並進運動を含む2リンク機構の運動方程式

図4に示すように,次に3次元空間で2つの球関節から構成される2リンク機構の運動方程式を考える.ここで,この2リンク機構の根本の関節$${\bm{p}_1}$$は固定されておらず,力$${\bm{f}_1}$$が作用し,並進運動の自由度を与えていることに注意をされたい.また,手先にトルク$${\bm{\tau}_E}$$も与えている.
全身運動における下肢や上肢の運動を切り出したと考えればよい.
前章終わりにも結果だけを示したが,この図4を見れば,関節に作用するトルクはその関節まわりの力のモーメントの和の形式で,すべての力と慣性力を加算するだけで良いことが予見される.そのことを以下に示す.
なお,部位1の近位側の関節を「関節1」,部位2の近位側の関節を「関節2」と呼ぶこととする.また,関節1,関節2の角変位ベクトルを$${\bm{q}_1, \bm{q}_2}$$とすると,その相対角変位ベクトルを$${\bm{Q}_1 \equiv \bm{q}_1, \bm{Q}_2 \equiv \bm{q}_2-\bm{q}_1}$$とする.
外力
関節1にはトルク$${\bm{\tau}_1}$$が作用し,前述の1リンク機構では関節1は固定されていたので,関節に作用する力は仕事を行わないので無視できた.しかし,ここでは関節1の位置ベクトル$${\bm{p}_1}$$は運動するため,関節1に作用する力$${\bm{f}_1}$$も考慮する.また,末端$${\bm{x}}$$には力$${\bm{f}_E}$$とトルク$${\bm{\tau}_E}$$が作用する.これは,たとえば下肢に作用する床反力の摩擦のモーメント(一般にフリーモーメントと呼ばれる)に相当すると考えればよい.
系と環境の境界が接する部分に作用する力と,重力も含めて外力である.
なお,前述したが,「身体に作用する力」として身体の運動方程式の外力は定義されているので,外力の座標系の定義や符号に注意をされたい.
内力
一方,系の内部にある関節2には力$${\bm{f}_2}$$とトルク$${\bm{\tau}_2}$$が作用するが,各部位の相対角変位ベクトルを$${\bm{Q}_1, \bm{Q}_2}$$とし,各部位の角速度ベクトルを$${\bm{\omega}_1, \bm{\omega}_2}$$とし,関節1と2における相対角速度を
$$
\begin{aligned}
\bm{\Omega}_1 &\equiv \bm{\omega}_1
\\
\bm{\Omega}_2 &\equiv \bm{\omega}_2 - \bm{\omega}_1
\end{aligned}
$$
とし,関節1と2と末端において,この相対角速度に対応する仮想変位を$${\delta \bm{p}_1, \delta \bm{Q}_1, \delta \bm{p}_2, \delta \bm{Q}_2, \delta \bm{x}}$$とする.
また,関節2に作用する力とトルクの仮想仕事は
$$
\begin{aligned}
\bm{f}_2^T \delta \bm{x}_2 + (-\bm{f}_2)^T \delta \bm{x}_2 &= 0
\\
\bm{\tau}_2^T \delta \bm{\Omega}_2 + (-\bm{\tau}_2)^T \delta \bm{\Omega}_2 &= 0
\end{aligned}
$$
のように打ち消し合うので無視してよい.このような系内に作用し打ち消し合う力を内力(internal force)と呼び,$${\bm{f}_2, \bm{\tau}_2}$$は相互作用する力であり,作用反作用力であり,その結果仕事は互いに打ち消しあうので,内力となる.すなわち,関節の角変位を相対角度で定義すれば,多体系の「系内」の関節に作用する力は,仮想仕事の原理ではすべて無視して良いことになる.
仮想仕事の原理
1リンク機構と比較し2リンク機構では,慣性力を含めると少し多くの力が作用するので,記号の整理を行う.図4と見比べていただきたい.
仮想仕事の原理で考慮すべき力は,10種類の力が作用するが,整理し$${\mathcal{M}_1, \mathcal{M}_2, \mathcal{F}_1, \mathcal{F}_2, \bm{\tau}_1, \bm{\tau}_E, \bm{f}_1, \bm{f}_E}$$の8つの力が作用すると考える.ここで,$${\mathcal{M}_1, \mathcal{M}_2, \mathcal{F}_1, \mathcal{F}_2}$$の定義は,
$$
\begin{aligned}
\mathcal{M}_1 &= \bm{I} _1 \dot{\bm{\omega}_1} + \bm{\omega}_1 \times \bm{I}_1 \bm{\omega}_1
\\
\mathcal{M}_2 &= \bm{I} _2 \dot{\bm{\omega}_2} + \bm{\omega}_2 \times \bm{I}_2 \bm{\omega}_2
\\
\mathcal{F}_1 &= m_1(\ddot{\bm{p}}_{g1}-\bm{g})
\\
\mathcal{F}_2 &= m_2(\ddot{\bm{p}}_{g2}-\bm{g})
\end{aligned}
$$
とし,$${\mathcal{M}_1, \mathcal{M}_2}$$は回転の慣性力,$${\mathcal{F}_1, \mathcal{F}_2}$$は並進の慣性力に重力を加え,各部位の重心に作用する力として一つにまとめている.$${\bm{\tau}_1, \bm{\tau}_E, \bm{f}_1, \bm{f}_E}$$は関節1と末端$${\text{E}}$$に作用するトルク$${\bm{\tau}}$$と並進の力$${\bm{f}}$$である.
ここで,関節に作用するトルクが各部位に相対的に作用する回転力であることを意識し,仮想角変位の定義を
$$
\begin{aligned}
\delta \bm{q}_1 &= \delta \bm{Q}_1
\\
\delta \bm{q}_2 &= \delta \bm{Q}_1 + \delta \bm{Q}_2
%\\
%\delta \bm{q}_E &= -\delta \bm{q}_2 = -(\delta \bm{Q}_1 + \delta \bm{Q}_2)% + \delta \bm{Q}_E
\end{aligned}
$$
とする.1リンクの場合と同様に,仮想仕事の原理とダランベールの原理から
$$
\begin{aligned}
&\mathcal{M}_1^T \delta \bm{q}_1 + \mathcal{M}_2^T \delta \bm{q}_2 + (m_1 \ddot{\bm{p}}_{g1})^T \delta \bm{p}_{g1} + (m_2 \ddot{\bm{p}}_{g2})^T \delta \bm{p}_{g2} =
\\ &\hspace{1.0cm}
\bm{\tau}_1^T \delta \bm{Q}_1 + \bm{\tau}_E^T \delta \bm{q}_E + (m_1 \bm{g})^T \delta \bm{p}_{g1} + (m_2 \bm{g})^T \delta \bm{p}_{g2} + \bm{f}_E^T \delta \bm{x} + \bm{f}_1^T \delta \bm{p}_1
\\
&\mathcal{M}_1^T \delta \bm{q}_1 + \mathcal{M}_2^T \delta \bm{q}_2 + \mathcal{F}_1^T \delta \bm{p}_{g1} + \mathcal{F}_2^T \delta \bm{p}_{g2}=
\\ &\hspace{2.5cm} \bm{\tau}_1^T \delta \bm{Q}_1 + \bm{\tau}_E^T \delta \bm{q}_E + \bm{f}_E^T \delta \bm{x} + \bm{f}_1^T \delta \bm{p}_1
\end{aligned}
$$
を得る.ここで,
$$
\begin{aligned}
&\delta \bm{q}_1 = \frac{\partial \bm{q}_1}{\partial \bm{Q}_1} \delta \bm{Q}_1
,~
\delta \bm{q}_2 = \frac{\partial \bm{q}_2}{\partial \bm{Q}_1} \delta \bm{Q}_1
,~
\delta \bm{q}_E = \frac{\partial \bm{q}_E}{\partial \bm{Q}_1} \delta \bm{Q}_1
,~
\delta \bm{p}_{1} = \frac{\partial \bm{p}_{1}}{\partial \bm{Q}_1} \delta \bm{Q}_1
,\\
&\delta \bm{p}_{g1} = \frac{\partial \bm{p}_{g1}}{\partial \bm{Q}_1} \delta \bm{Q}_1
,~
\delta \bm{p}_{g2} = \frac{\partial \bm{p}_{g2}}{\partial \bm{Q}_1} \delta \bm{Q}_1
,~
\delta \bm{x} = \frac{\partial \bm{x}}{\partial \bm{Q}_1} \delta \bm{Q}_1
\end{aligned}
$$
であるので,1リンクモデルのときと同様に,
$$
\begin{aligned}
&\mathcal{M}_1^T \frac{\partial \bm{q}_1}{\partial \bm{Q}_1}+ \mathcal{M}_2^T \frac{\partial \bm{q}_2}{\partial \bm{Q}_1} + \mathcal{F}_1^T \frac{\partial \bm{p}_{g1}}{\partial \bm{Q}_1} + \mathcal{F}_2^T \frac{\partial \bm{p}_{g2}}{\partial \bm{Q}_1} =
\\ &\hspace{3.5cm}
\bm{\tau}_1^T \frac{\partial \bm{Q}_1}{\partial \bm{Q}_1} + \bm{\tau}_E^T \frac{\partial \bm{q}_E}{\partial \bm{Q}_1} + \bm{f}_E^T \frac{\partial \bm{x}}{\partial \bm{Q}_1} + \bm{f}_1^T \frac{\partial \bm{p}_1}{\partial \bm{Q}_1}
\\
&\mathcal{M}_1 + \mathcal{M}_2 + \left(\frac{\partial \bm{p}_{g1}}{\partial \bm{Q}_1}\right)^T \mathcal{F}_1 + \left(\frac{\partial \bm{p}_{g2}}{\partial \bm{Q}_1}\right)^T\mathcal{F}_2 =
\\
&\hspace{3.5cm}\bm{\tau}_1 +\bm{\tau}_E+ \left(\frac{\partial \bm{x}}{\partial \bm{Q}_1}\right)^T \bm{f}_E + \bm{0}
\end{aligned}
$$
を得る.2行目は,転置の順番を入れ替えている.また,
$$
\begin{aligned}
\frac{\partial \bm{q}_1}{\partial \bm{Q}_1} &= \frac{\partial \bm{Q}_1}{\partial \bm{Q}_1} = \bm{E}
\\
\frac{\partial \bm{q}_2}{\partial \bm{Q}_1} &= \frac{\partial (\bm{Q}_1+\bm{Q}_2)}{\partial \bm{Q}_1} = \bm{E}
\\
\frac{\partial \bm{q}_E}{\partial \bm{Q}_1} &= \frac{\partial (\bm{Q}_1+\bm{Q}_2)}{\partial \bm{Q}_1} = \bm{E}
\\
\frac{\partial \bm{q}_E}{\partial \bm{Q}_1} &= \frac{\partial (\bm{Q}_1+\bm{Q}_2)}{\partial \bm{Q}_1} = \bm{E}
\\
\frac{\partial \bm{p}_1}{\partial \bm{Q}_1} &= \bm{0}
\end{aligned}
$$
の結果も用いている.ここで,$${\bm{E}}$$は単位行列である.この他のヤコビ行列は「前章の図6」の前後に導出を示したが,
$$
\begin{aligned}
\bm{J}_{g1} &= \frac{\partial \bm{p}_{g1}}{\partial \bm{Q}_1} = \frac{\partial \dot{\bm{p}}_{g1}}{\partial \bm{\Omega}_1} = -[( \bm{p}_{g1} - \bm{p}_1) \times] = -[\bm{r}_1^{g1} \times]
\\
\bm{J}_{g2} &= \frac{\partial \bm{p}_{g2}}{\partial \bm{Q}_1} = \frac{\partial \dot{\bm{p}}_{g2}}{\partial \bm{\Omega}_1} = -[( \bm{p}_{g2} - \bm{p}_1) \times] = -[\bm{r}_1^{g2} \times]
\\
\bm{J}_x &= \frac{\partial \bm{x}}{\partial \bm{Q}_1} = \frac{\partial \dot{\bm{x}}}{\partial \bm{\Omega}_1} = -[( \bm{x} - \bm{p}_1) \times] = -[\bm{r}_1^{x} \times]
\\
\end{aligned}
$$
であるので,
$$
\begin{aligned}
\mathcal{M}_1 + \mathcal{M}_2 + \left(\frac{\partial \bm{p}_{g1}}{\partial \bm{Q}_1}\right)^T \mathcal{F}_1 + \left(\frac{\partial \bm{p}_{g2}}{\partial \bm{Q}_1}\right)^T\mathcal{F}_2&= \bm{\tau}_1 +\bm{\tau}_E+ \left(\frac{\partial \bm{x}}{\partial \bm{Q}_1}\right)^T \bm{f}_E
\\
\mathcal{M}_1 + \mathcal{M}_2 + \bm{J}_{g1} ^T \mathcal{F}_1 + \bm{J}_{g1}^T \mathcal{F}_2&= \bm{\tau}_1 +\bm{\tau}_E+ \bm{J}_{x}^T \bm{f}_E
\\
\mathcal{M}_1 + \mathcal{M}_2 -[\bm{r}_1^{g1} \times]^T \mathcal{F}_1 -[\bm{r}_1^{g2} \times]^T \mathcal{F}_2&= \bm{\tau}_1 +\bm{\tau}_E-[\bm{r}_1^{x} \times]^T \bm{f}_E
\\
\mathcal{M}_1 + \mathcal{M}_2 + [\bm{r}_1^{g1} \times] \mathcal{F}_1 +[\bm{r}_1^{g2} \times] \mathcal{F}_2&= \bm{\tau}_1 + \bm{\tau}_E +[\bm{r}_1^{x} \times] \bm{f}_E
\end{aligned}
$$
を得る.
結果のまとめ
関節1に作用するトルク
これを$${\bm{\tau}_1}$$について整理すると,関節1に作用するトルク
$$
\bm{\tau}_1 = \mathcal{M}_1 + \mathcal{M}_2 + [\bm{r}_1^{g1} \times] \mathcal{F}_1 + [\bm{r}_1^{g2} \times] \mathcal{F}_2 - \bm{\tau}_E - [\bm{r}_1^{x} \times] \bm{f}_E
$$
を得る.図4を再度示すが,

式と図4を見比べていただきたい.関節に作用するトルク$${\bm{\tau}_1}$$のうち,力のモーメントはすべて関節1まわりの力のモーメントで記述されている.もはや,関節2の位置$${\bm{p}_2}$$は運動方程式には表れておらず,みかけ上,関節2の位置がどこにあっても構わず,関節に作用するトルク$${\bm{\tau}_1}$$もトルク$${\bm{\tau}_2}$$と独立に定まっている.
関節2に作用するトルク
詳細は示さないが,1リンク機構の結果などを利用し,同様に$${\bm{\tau}_2}$$は
$$
\bm{\tau}_2 = \mathcal{M}_2 + [\bm{r}_2^{g2} \times] \mathcal{F}_2 - \bm{\tau}_E - [\bm{r}_1^{x} \times] \bm{f}_E
$$
となる.すべて関節2まわりのモーメントとして記述されている.
並進のダイナミクス
並進の運動方程式は
$$
\bm{f}_1 = \mathcal{F}_1 + \mathcal{F}_2 - \bm{f}_E
$$
となる.
多体系のニュートン・オイラーの運動方程式

以上をまとめると,
$$
\begin{aligned}
\bm{T} &=
\bm{J}_{\mathcal{M}}^T
\begin{bmatrix}
\mathcal{M}_1 \\ \mathcal{M}_2
\end{bmatrix}
+
\bm{J}_{\mathcal{F}}^T
\begin{bmatrix}
\mathcal{F}_1 \\ \mathcal{F}_2
\end{bmatrix}
-
\bm{J}_{E}^T
\begin{bmatrix} \bm{f}_E \\ \bm{\tau}_E \end{bmatrix}
\\
\begin{bmatrix} \bm{f}_1 \\ \bm{\tau}_1 \\ \bm{\tau}_2 \end{bmatrix} &=
\begin{bmatrix}
\bm{0} & \bm{0} \\ \bm{E} & \bm{E} \\ \bm{0} & \bm{E}
\end{bmatrix}
\begin{bmatrix}
\mathcal{M}_1 \\ \mathcal{M}_2
\end{bmatrix}
+
\begin{bmatrix}
\bm{E} & \bm{E} \\ [\bm{r}_1^{g1} \times] & [\bm{r}_1^{g2} \times] \\ \bm{0} & [\bm{r}_2^{g2} \times]
\end{bmatrix}
\begin{bmatrix}
\mathcal{F}_1 \\ \mathcal{F}_2
\end{bmatrix}
-
\begin{bmatrix}
\bm{E} & \bm{0} \\ [\bm{r}_1^{x} \times] & \bm{E} \\ [\bm{r}_2^{x} \times] & \bm{E}
\end{bmatrix}
\begin{bmatrix} \bm{f}_E \\ \bm{\tau}_E \end{bmatrix}
\end{aligned}
$$
のように,まとめることができる.右辺の第1項は,回転の慣性力に関する項.第2項は各部位の重心に作用する並進の慣性力と重力に関する慣性力項,第3項は外力に関する項である.外力のヤコビ行列の符号が負になっていることに注意をされたい.
関節1と2に作用するトルクは,その関節まわりのモーメントで記述され,全方程式を線形な式で記述することができる.
もし,リンク数や外力が増えても,基本的にルールは同じであるので,システマティックに運動方程式を立てることができる.
なお,ここで導いた結果は第14章
で述べた結果と一致することを確認していただけたらと思う.
関節に作用するトルクの一般化
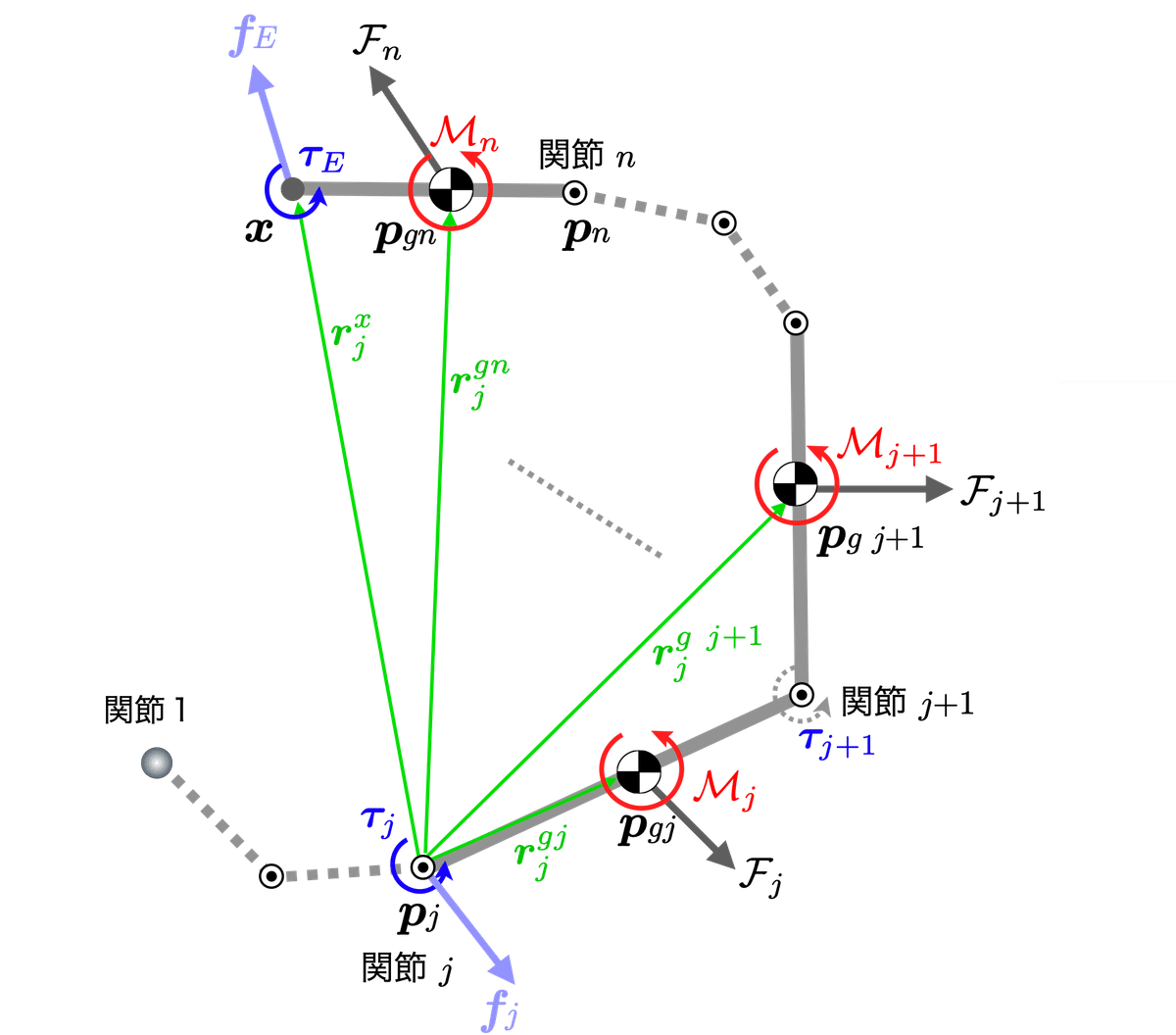
この議論の延長で自由度を拡張し一般化する.$${n}$$個のシリアルリンクの場合の,$${j}$$番目の関節に作用するトルク$${\bm{\tau}_j}$$は
$$
\begin{aligned}
\bm{\tau}_j &= \sum_{i=j}^n \mathcal{M}_i + \sum_{i=j}^n [\bm{r}_j^{gi} \times] \mathcal{F}_i - \bm{\tau}_E - [\bm{r}_j^{x} \times] \bm{f}_E
\\
\mathcal{M}_i &= \bm{I}_i \dot{\bm{\omega}_i} + \bm{\omega}_i \times \bm{I}_i \bm{\omega}_i
\\
\mathcal{F}_i &= m_i (\ddot{\bm{p}}_{gi}-\bm{g})
\end{aligned}
$$
とすれば良い.ここで,$${\bm{r}_j^{gi}, \bm{r}_j^{x}}$$は,関節$${j}$$からみた,リンク$${i}$$の重心と外力$${\bm{f}_E}$$が作用する位置の,位置ベクトルを示している.
まとめ
関節に作用するトルクは,漸化的ニュートン・オイラーの運動方程式からも,合成の運動方程式からも算出することができ,数値的に効率よく解きたい際には,前者を使用するのが良いだろう.もし,関節に作用するトルクの物理的意味を問いたいなら,後者の合成の運動方程式をもちいるのがよい.また,この章のように導出し,3リンク以上の多リンク機構でも同様に考えればよい.
なお,第14章の後半に議論したことは,先程の式のうち回転の運動方程式だけ抜き出し,
$$
\begin{aligned}
\bar{\bm{T}} &=
\bar{\bm{J}}_{\mathcal{M}}^T
\begin{bmatrix}
\mathcal{M}_1 \\ \mathcal{M}_2
\end{bmatrix}
+
\bar{\bm{J}}_{\mathcal{F}}^T
\begin{bmatrix}
\mathcal{F}_1 \\ \mathcal{F}_2
\end{bmatrix}
-
\bar{\bm{J}}_{E}^T
\begin{bmatrix} \bm{f}_E \\ \bm{\tau}_E \end{bmatrix}
\\
%
\begin{bmatrix} \bm{\tau}_1 \\ \bm{\tau}_2 \end{bmatrix} &=
\begin{bmatrix}
\bm{E} & \bm{E} \\ \bm{0} & \bm{E}
\end{bmatrix}
\begin{bmatrix}
\mathcal{M}_1 \\ \mathcal{M}_2
\end{bmatrix}
+
\begin{bmatrix}
[\bm{r}_1^{g1} \times] & [\bm{r}_1^{g2} \times] \\ \bm{0} & [\bm{r}_2^{g2} \times]
\end{bmatrix}
\begin{bmatrix}
\mathcal{F}_1 \\ \mathcal{F}_2
\end{bmatrix}
-
\begin{bmatrix}
[\bm{r}_1^{x} \times] & \bm{E} \\ [\bm{r}_2^{x} \times] & \bm{E}
\end{bmatrix}
\begin{bmatrix} \bm{f}_E \\ \bm{\tau}_E \end{bmatrix}
\end{aligned}
$$
の式において,外力$${\bm{f}_E}$$に近い部位では
$$
\bar{\bm{J}}_{\mathcal{M}}^T
\begin{bmatrix}
\mathcal{M}_1 \\ \mathcal{M}_2
\end{bmatrix} \text{と}
\bar{\bm{J}}_{E}^T \begin{bmatrix} \bm{f}_E \\ \bm{\tau}_E \end{bmatrix}
$$
の右辺第1項の慣性力項と,第3項の外力を比較し,同様に,
$$
\bar{\bm{J}}_{\mathcal{F}}^T
\begin{bmatrix}
\mathcal{F}_1 \\ \mathcal{F}_2
\end{bmatrix}
\text{と}
\bar{\bm{J}}_{E}^T \begin{bmatrix} \bm{f}_E \\ \bm{\tau}_E \end{bmatrix}
$$
の右辺第2項の慣性力項と,第3項の外力を比較すると,「慣性力項が外力項よりも小さく無視でき」,以下のように
$$
\begin{aligned}
\begin{bmatrix} \bm{\tau}_1 \\ \bm{\tau}_2 \end{bmatrix} \approx
-
\bar{\bm{J}_{E}}
\begin{bmatrix} \bm{f}_E^T \\ \bm{\tau}_E \end{bmatrix} =
- \begin{bmatrix} [\bm{r}_1^{x} \times] \bm{f}_E + \bm{\tau}_E \\
[\bm{r}_2^{x} \times] \bm{f}_E + \bm{\tau}_E
\end{bmatrix}
\end{aligned}
$$
という「静力学関係」として運動方程式が近似できることを示している.このことが意味することは,すでに14章で述べたので,そちらをご覧になっていただきたい.
ひとつだけ,繰り返し述べるなら,このことは姿勢で議論ができることを示している.前にも述べたが,外積の幾何学的意味が理解できれば,トルクを発揮できる良い姿勢などを議論ができる.具体的には,$${[\bm{r}_1^{x} \times] \bm{f}_E, [\bm{r}_2^{x} \times] \bm{f}_E}$$で,すなわち,床反力のような外力$${\bm{f}_E}$$と,ベクトル$${\bm{r}_1^{x}, \bm{r}_2^{x}}$$との外積で,関節に作用するトルクが定まることを示している.これは,きわめて直感的だ.
また,大きな外力が作用する近辺で慣性項が小さいということは,動力生成・伝達のためには「ヒトは関節を動かさないように」制御し,むしろ「関節がぐらつかない」ことが重要であることを示唆している.バッティングや投球などを例に考えると,下肢などの地面反力の影響を受ける部位では,まったく動かさないことは不可能だが加速度を小さくすることで慣性力を小さくすることが重要だ.大きな動力を生成するためには,腰を速く動かすことはあまり意味がないことを示唆している.この議論は,またどこかで行いたいが,身体運動において重要な意味を持つ.
このように第14章と同じ結果を導いただけだが,ヤコビ行列を用いることで,合成の運動方程式の物理的意味を簡潔にまとめて整理することができる.
ここでは,詳しく述べなかったが,ここで述べた導出方法は仮想パワーの原理(principle of virtual power)やJourdainの原理(Jourdain principle)と呼ばれる方法で,マルチボディダイナミクス(multibody dynamics)などでは使用される方法である(文献1,3参照).自由度が高いシステムなら,第14章のように合成の運動方程式から導出するよりは容易である.
外積を利用したヤコビ行列を用いて記述することのもう一つの利点は,三角関数や角度の定義を行う必要がないことである.多関節系ではこのことも多大な利点をもたらす.精度や計算量の観点から,3次元空間では特別な例を除いて可能な限り三角関数で運動を表現しないことが賢明だ.
次章では,もう少しだけ例を取り上げ,Pythonによる具体的な計算例を示す予定である.
参考文献
1)清水,今西著,日本機械学会編,コンピュータダイナミクスシリーズ 3,マルチボディダイナミクス(1)-基礎理論 -,コロナ社,2006.(残念ながら絶版)
2)西川ら,ヤコビ行列を用いた静力学による着地動作解析,シンポジウム: スポーツ・アンド・ヒューマン・ダイナミクス講演論文集,108, 2013
3)太田ら,Jourdainの原理に基づく逆動力学解析に適した全身の運動方程式の導出,シンポジウム:スポーツ工学・ヒューマン・ダイナミクス,C1,2015



【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
【データの計測について】
スポーツセンシング社のスタジオで,フォースプレートやモーションキャプチャを利用した計測も行えます.出力されるデータと,ここで示したプログラム(入力データの取り込み関数を少々改変する必要があるが)で,同様な解析を行えますので,まずはお気軽にお問い合わせください.
