
動かして学ぶバイオメカニクス #26 〜道具の慣性モーメント計測〜
習熟した全身運動では道具が身体化されるという議論もある.一般に道具がパフォーマンスの最終出力位置に近く,道具の慣性は身体運動に強く拘束することが多い.そのような身体運動の力学計算では,身体の質量や慣性モーメントだけでなく,バットやクラブなどの道具のパラメータが必要である.ところが,身体の質量や慣性モーメントなどのパラメータを推定するモデルはこれまで示してきたが,道具の慣性モーメントは未知のときが多く自分で計測するしかない.そこで,ここでは慣性モーメントを計測する方法と原理について述べる.
(追記:230713)日本野球機構(NPB)と日本野球連盟(JABA)の硬式ボールの慣性モーメントを計測した結果を加筆した.
はじめに
身体の力学計算では,身体をいくつかの部位に(ここでは15の部位に)分割し,統計モデルから推定した各部位の質量や慣性モーメント(moment of inertia)を利用し,運動方程式を解くことになる.幸い,身体に関しては体重などから各部位の慣性モーメントを推定するモデルが準備されているが,道具の慣性モーメントは既知ではないことが多い.そこで,自分で計測を行うか,物体の形状と密度などから推定を行う必要がある.
慣性モーメント,慣性テンソルについては
を参照していただきたい.
身体の慣性モーメントの推定モデルは,身体の形状計測を行い(特徴点だけで代用することも),密度一定と仮定して計算するだけだ.Chandlerのレポート(文献1)のように,屍体(cadaver)から慣性モーメントの計測モデルは稀で,通常は形状から推定を行うしかない.慣性モーメントの数理的な原理が理解できていれば,形状さえわかれば計算が簡単であることは想像できるが,そのように推定した慣性モーメントなので,さほど信頼性も高くはないことも念頭に置いておくべきだろう.そもそも運動中,身体の形状も容易に変化する.
一方,例えばバットなどの道具の慣性モーメントを手軽に知りたいとき,形状を計測するも面倒だ.手軽さを考えると別な方法が必要となる.
物体の慣性モーメントを正確に計測を行うためには,専用の計測機器を利用して計測する必要があり,これらはかなり高価で,サービスを利用して計測を依頼してもかなりの料金を請求されるのが一般的だ.ただし,これらの計測でも機械振動を行わせて計測するのが基本で,工夫すれば,手作りの装置で多少精度を向上させることも可能だろう.また,これまでも言及してきたが,慣性モーメントの精度よりも,運動学的なデータの精度を向上することが先決で,それが解決できない状態では,それほど慣性モーメントの精度に神経質になることもないだろう.筆者もお手製の粗末な道具で,かなり精度は低いと思われるが,クラブやボールの慣性モーメントを推定している.
ここでは,機械振動を利用して,物体の慣性モーメントを計測する方法について述べていく.基本的な原理は簡単だ.大学の物理学実験では,正確な物体の形状や密度などから慣性モーメントが既知である物体を振動させ,振動周期を計測することで重力加速度$${g}$$を推定するという実験があるが,慣性モーメントの推定では振動周期を計測する実験を行い重力加速度を既知として,反対に慣性モーメントを推定する.したがって,理科年表などで測定する場所の重力加速度$${g}$$を調べておくとよいだろう.なお,重力加速度$${g}$$は場所で異なり,稚内で9.806,宮古島で9.790,上野で9.797 [m/s$${^2}$$]程度である.ただし,様々な計測誤差を考えると,9.8で十分だろう.
したがって慣性モーメントの推定は,機械振動の力学について理解しておく必要があり,ここでは簡単に復習し,慣性モーメントの推定方法について述べていく.振動の基礎だけ理解できれば良いので,読者は力学の教科書等で単振動などについて復習または学習していだきたい.これらについて学んでいれば,計測の実際のところだけ読めば十分であろう.
いずれにせよ慣性モーメントを測定する作業は,振動の運動方程式をたて,その周期から慣性モーメントを計算する作業となるが,平行軸の定理や,単振動の原理を理解し,対象とする運動の運動方程式を適切に立てる力を養うことが肝要だ.
振動の力学
単振り子

振動の基本も運動方程式である.導入として,単振り子の単振動をまず考える.伸縮せず,質量が無視できる程度の軽い糸(または棒)を上端点$${O}$$に固定し,下端に十分小さい重りをつるし,糸が常に一つの鉛直面内で振動する振り子を単振り子(simple pendulum)と呼ぶ.ここで,重りの質量を$${m}$$,糸の長さを$${l}$$,鉛直方向に対する糸の傾きを$${\psi}$$とすると,重りの点$${O}$$まわりの慣性モーメントは$${I = m l^2}$$となる.また,重りの接線方向に作用する力が$${-mg \sin \psi}$$($${\psi}$$方向を正とする)となり,これに起因する振り子を回転させる力のモーメント(復元モーメント, restoring moment)は$${-mgl \sin \psi}$$となるため,空気抵抗を無視し,重りの回転(接線)方向の運動方程式を考えると
$$
I \ddot{\psi} = -mgl \sin \psi \\
ml^2 \ddot{\psi} = -mgl \sin \psi
\\
\ddot{\psi} = - \frac{g}{l} \sin \psi
$$
となる.角度$${\psi}$$に関する微分方程式として考えると,これは非線形の微分方程式となり,簡単に解くことはできない.
なお,$${\sin \psi}$$は,テイラー展開によって
$$
\sin \psi = \psi - \frac{\psi^3}{3!} + \frac{\psi^5}{5!} - \cdots
$$
と書け,角度$${\psi}$$が十分小さいとき($${\psi \ll 1}$$)には,高次の項は小さくなり無視できるため,
$$
\sin \psi \approx \psi
$$
と近似できるので,前述の微分方程式は
$$
\ddot{\psi} = - \frac{g}{l} \psi
$$
のような線形化された($${\psi}$$に比例した形式で書かれた)運動方程式となり,この形式では解きやすくなる.ただし,この解はこの近似($${\sin \psi \approx \psi}$$)の微小角でしか成り立たないことに注意されたい.つまり,大きく振動させてはいけない.
ここで,この運動方程式は重りの質量$${m}$$と無関係に,糸の長さ$${l}$$で定まる式となっているが,右辺の力は重りの鉛直方向に対する角度$${\psi}$$に反比例し,この鉛直軸に向かう引力に相当し,鉛直軸から離れるほど鉛直軸に戻そうとする力が作用するので,これを復元力(restoring force)と呼ぶ.
なお,慣性モーメントの単位は[$${\mathrm{kg ~m}^2}$$]である.
そこで,次にこのような復元力が作用する運動が,最も単純な振動,すなわち後述する単振動となることを示す.
単振り子の運動方程式
この微分方程式は,二階の斉次(同次)線形微分方程式で
$$
\ddot{\psi} + \frac{g}{l} \psi = 0
$$
と書くことができた.ここで, 斉次(同次,homogeneous)とは変数$${\psi}$$に関する項を全て左辺に書くことができ,右辺が$${0}$$となることを指す.もし,$${\psi}$$の項を含まない項が存在すれば,それは非斉次(非同次, in homogeneous)となる.
ちなみに,ここで質量$${m}$$を質量とし,$${\frac{g}{l}=\frac{k}{m}, x =\psi}$$とおくと,前式は,
$$
m \ddot{x} = - k x
$$
と書き換えることができる.これは質量とバネ(図2)の式となり,これは単振動の式となることが知られているので,先程の近似式も単振動の運動方程式ということが予想される.

この線形斉次微分方程式を解くために,
$$
\psi (t)= e^{ct}
$$
と置く.ここで$${c}$$は定数である.すると,
$$
\dot{\psi} (t)= c e^{ct}, ~~\ddot{\psi} (t)= c^2 e^{ct}
$$
となることが知られているので,これを先程の二階斉次線形微分方程式に代入し,オイラーの公式を利用することで,$${\psi}$$の解
$$
\psi (t) = a \cos \left( \sqrt{\frac{g}{l}} t + \alpha\right)
$$
を得る事ができる(証明は補足1を参照).
これは単振動(simple harmonic motion)の式にほかならない.
単振動

単振動(調和振動,simple harmonic motion)は幾何学的に等速円運動する点Pをオレンジ色の面の一直線上に投影した点の運動として定義できる.
原点Oのまわりを一定の速度$${\omega}$$で回転する半径$${a}$$の点Pを,$${x}$$軸に投影した時間軸$${t}$$の関数としたグラフを示している.
これは,
$$
x(t) = a \cos \left( \omega t + \alpha\right)
$$
と記述され,先程の単振り子の式と似ており,$${\psi(t)}$$の式と見比べて
$$
\omega = \sqrt{\frac{g}{l}}
$$
とした単振動と考えればよい.
ここで,$${a}$$は振幅(amplitude),$${\omega}$$は角振動数(angular frequency),$${\theta = \omega t + \alpha}$$は位相(phase),$${\alpha}$$は初期位相(initial phase)と呼ばれる.この振動の周期$${T}$$と$${\omega}$$の間には
$$
T = \frac{2 \pi}{\omega}=2\pi \sqrt{\frac{l}{g}}
$$
の関係がある.また,単位時間あたり(1秒あたり)の点Pの回転数$${f}$$を振動数(frequency)と呼び,これは
$$
f = \frac{1}{T} = \frac{\omega}{2 \pi} =\frac{1}{2 \pi}\sqrt{\frac{g}{l}}
$$
で与えられる.振動数$${f}$$の単位はヘルツ [Hz],角振動数$${\omega}$$の単位は[rad/s]を用いる.
物理振り子

単振り子は,質点の振り子であるが,バットなど実際の物体には大きさがあるので,ここで点Oを通る水平軸まわりに振動する「剛体」の振動を考える.これを物理振り子(実体振り子,phsical pendulum)と呼ぶ.
ここで剛体の質量を$${m}$$,Oまわりの慣性モーメントを$${I}$$,回転角を$${\psi}$$,Oから重心Gまでの距離を$${h}$$とすると,この剛体の軸まわりの回転の運動方程式は,
$$
I \ddot{\psi} = - mgh \sin{\psi}
$$
となる.単振り子と同様に回転角$${\psi}$$が小さいときは
$$
I \ddot{\psi} = - mgh \psi
\\
\ddot{\psi} + \frac{mgh}{I} \psi = 0
$$
となる.重心Gに作用する力を剛体に作用する代表の力として考えれば,単振り子と同様に,その回転(接線)方向に作用する力$${-mgh \sin{\psi}}$$が剛体に作用する復元モーメントとなる.このとき,周期$${T}$$はこれまでの結果を利用し,
$$
T = \frac{2 \pi}{\omega}=2\pi \sqrt{\frac{I}{mgh}}
$$
となるので,物理振り子の単振動となるように振動角度を小さくし,周期$${T}$$を計測すれば,
$$
T^2 = \frac{4\pi^2I}{mgh}
\\
I = \frac{mghT^2}{4\pi^2}
$$
から慣性モーメント$${I}$$を推定できる.すなわち,物体の質料$${m}$$と,物体がバランスする点を計測することでOから重心Gまでの距離$${h}$$を計測し,周期Tを計測することで慣性モーメントを知ることができる.
二本つり振り子
実際に物体に物理振り子として振動を与えようと,安定して振動を行わせるのが難しい時がある.そのような際,2つの糸で剛体を支えることで振動を安定させることができることがある.
その場合でも,振動角を小さくすることで,単振動となり,慣性モーメントを計測できる.

そこで,図5のように2本の長さ$${a}$$の長い糸で水平につるした棒について考え,棒の中心を通る鉛直軸まわりに$${\psi}$$だけ回す振動を考える(図5上方).棒は一様で,質量$${m}$$,長さ$${2l}$$,また中心を通る鉛直軸まわりの慣性モーメントを$${I}$$とする.
一方,振り子の横から眺めると(図5側方),糸に作用する張力を$${T}$$,糸の長さを$${a}$$,糸と鉛直線となす角度を$${\theta}$$とする.
そこで,いつものように振動の運動方程式をたてるために,復元モーメントについて考えると,側方から見た図から糸に作用する張力の水平成分は$${T \sin \theta}$$となり,また鉛直成分に関しては,幾何学的に
$$
T \cos \theta = \frac{1}{2} mg
\\
T = \frac{1}{2\cos \theta} mg
\approx \frac{1}{2} mg
$$
という関係が成り立つ.ここで,$${1/2}$$としているのは2本の糸で棒をつっているからで,角度が$${\theta \ll 1}$$のように十分小さい際の近似($${\cos \theta \approx 1}$$)を用いている.また,復元力として,先程の単振り子では接線方向を考えていたが,いまは水平方向を考えている点が,少し異なるので注意されたい.
次に側方から見た図と,上方から見た図では,それぞれ角度$${\theta, \psi}$$が定義されているので,これらの幾何学的関係を考える.緑色の破線の長さには
$$
l \sin \psi = a \sin \theta
$$
の関係が成り立つ.さらにここで,$${\theta \ll 1, \psi \ll 1}$$のように十分小さい角度とすると,
$$
l \psi \approx a \theta
\\
\theta \approx \frac{l}{a} \psi
$$
と近似できる.
すると,水平方向の2本の糸の復元モーメント$${N}$$は
$$
N = -2 l (T \sin \theta) = \approx -2T l \theta
$$
となる.これは$${\theta \ll 1}$$を用いている.さらに先程の幾何学的関係($${T \approx \frac{1}{2} mg, \theta \approx \frac{l}{2a} \psi}$$)を用いて,復元モーメント$${N}$$
$$
N = -2Tl \theta
\approx -2\frac{1}{2} mg l \theta \approx -mg l (\frac{l}{a} \psi) = -\frac{mgl^2}{a} \psi
$$
を得る.
少し複雑な流れであったが,
上方から見た2本つり振り子の運動方程式は
$$
I \ddot{\psi} = -\frac{mgl^2}{a} \psi
\\
\ddot{\psi} = -\frac{mgl^2}{aI} \psi
$$
となるので,単振動の運動方程式
$$
\ddot{\psi} = -\omega^2 \psi
$$
と見比べれば,角振動数が$${\omega^2 = \frac{mgl^2}{aI}}$$なので,単振動の周期は
$$
T = \frac{2 \pi}{\omega}
\\
T= \frac{2\pi}{l} \sqrt{\frac{aI}{mg}}
$$
となり,慣性モーメント
$$
I = \frac{mg l^2 T^2}{4\pi^2 a}
$$
を得る.
平行軸の定理の利用
小さなボールのような物体を2本の糸でつりさげて,安定な単振動を起こすことは一般に困難なので,大きな物体にボールを固定し,物体単独と,物体+ボールの合成慣性モーメントを計測することでボールの慣性モーメントを計測することができる.
下記に示すボールの例では,平行軸の定理を利用しないが,合成の慣性モーメントを計算する際には平行軸の定理を用いれば良い.
慣性モーメントの平行軸の定理については
を参照されたい.
例:ボールの慣性モーメント計測
ボールのような物体の慣性モーメント$${I_b}$$を計測する場合,

ボールを支えるために中心に穴の空いた板を4つの糸でつり,さらにそれを図6のように2本の糸でつることで,板を支えている.したがって,4つの糸でつっている三角形以下のボールと板の慣性モーメントを計測することになり,これは三角形以下の物体の2本つり振り子の運動方程式となる.ただし糸の重さは無視することとする.
そこで板の中央の鉛直線まわりの慣性モーメントを$${I_p}$$とすると,板の慣性モーメント$${I_p}$$と,図6のようにボールと板を合わせた慣性モーメント$${I_p + I_b}$$を計測することで,ボールの慣性モーメントを推定できる.
この場合は,振動の中心軸に対して,板もボールも中心軸にあわせているので,平行軸の定理を利用することなく計算ができる.
例題
図6に示した道具を使用して,周期を計測した例を示すので,実際にボールの慣性モーメントを計算してみよう.答えは最後に示す.
慣性モーメントの推定の実際
振動周期を定めるために,10周期($${10T}$$)の振動を計測し,0.1倍することで周期$${T}$$を算出するとよい.
また,単振動となるように振幅が大きくならないように注意されたい.
Pythonをつかって解くというほど大げさではなく,簡単に計算できるが,実際に周期を測った例を上げるので,ご自身でボールの慣性モーメントを計算してみるとよいだろう.
下記の表は,図6の2本つり振り子の振動の10周期計測を行った時間である.
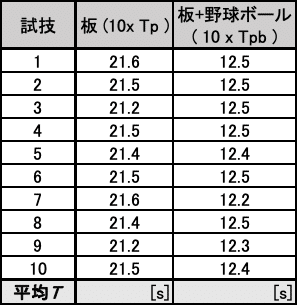
また,板とボールの質量はそれぞれ$${m_p=0.060, m_b = 0.145}$$ [kg],糸の長さ$${a=1.76}$$[m],回転中心から糸までの距離$${l = 0.142}$$ [m]であった.
ここで計算するとをわかるが,2乗の項の精度がきいてくるので,回転中心から糸までの距離と周期$${l, T}$$の計測は特に精度良く行いたい.
実際に振動させるとわかるが,10周期の間に減衰もあり,回転は安定しないので,さらに精度よく計測するためには,摩擦を減らし,振動が正確になるように構造を見直すとよいだろう.
追記(230713):計測の実際と注意点
手作りの装置での実験には限界があるが,ここでは,できるだけ計測精度を高めるための注意点を述べる.ここでは図6の例に相当し,野球の公式NPBボールと公式JABAボールで計測した例を取り上げて述べる.
慣性モーメントの計測装置と異なり,一つ一つのパラメータの計測精度を高め,かつ安定した振動を行わせる必要があり,少しの誤差で,慣性モーメントは大きく値を変えるので,非常に繊細な実験となる.
長さの計測精度もできるだけ向上させる必要がある.特に2本つり振動の$${l}$$はその2乗を計算に使用するため,可能な限り精度を高める必要がある.また,慣性モーメントは振動周期$${T}$$に対しても2乗に比例する.ストップウォッチによる時間の計測では精度を担保できないので,モーションキャプチャなどを利用するとよいだろう.この後示すように,モーションキャプチャであれば,振動が安定しているか,不安定かの判定も可能である.不安定は計測は除外したほうが良い.
糸は伸縮してはいけないので,できるだけ細くて強い糸が望ましい.ここでは0.25 [mm]の太さのケブラー糸を使用しているが,摩擦も少ないので,回転周期の減衰も少なく,使用する糸の一つの候補である.ケブラー糸はAmazonでも入手できる.見た目は,通常の裁縫用の糸と違いがない.
ボールや板などの質量も,0.1 g単位で計測するのが望ましい.
振幅が小さく,回転の中心が一定になるようにも気をつけたい.
上記の動画の計測で計測したNPBボールでは,振動の中心を一定にすることは難しく,モーションキャプチャを使用し正確に周期$${T}$$を計測しても,ばらつき発生した.
ここで安定していない振動の例を示そう.ボールを載せている板の四隅には反射マーカを配置していて,計測を行っている.ここでは,特に示さないが,どのマーカを使用しても,水平のXY軸のどちらを使用しても周期の計算の結果に大きな違いはない.
図7は,4つのうちの1つのマーカの挙動を示す.

図8に,このうちx,y座標だけを示すが,変化量をわかりやすくするため,それぞれ平均値で減算している.

一方,比較的安定し,振幅も小さめの振動では図9のようなxy座標を示す
.

振動周期の計算例
周期の計算を適切に計算しないと,結果が大きく異なる.そこで,ここでは,注意深く周期を計算した例を示す.
図9のx座標の最大値と最小値となる『極大点(黒点)は,x座標の時間微分(速度)が0と交差する点』から計算する(図10参照).このとき点と点の時間間隔は,二分の一周期に相当することに注意をされたい.
さて,データにはノイズが含まれるので,生データから単純に極大値(最大値と最小値)を選択しても正確には得ることができない.そこで,図9の波形を平滑化スプライン(smoothing spline)で微分した関数(速度関数)を計算し,その曲線とy=0との交点を極大値として算出する.
平滑化スプラインは
を参照されたい.
intersection()関数の利用
Pythonでは,交点を算出するには関数intersection() を利用すればよい.
もし,ご利用のPython環境にitersectがない場合(importできない場合)は,コマンドラインで
pip install intersectとしてインストールしていただきたい.JupyterLabでは
!pip install intersectとすればよい.intersectをインストールした後に,
from intersect import intersectionとすることで,モジュールのインポートができ,準備が整う.
intersection()関数は,2つの曲線を,グラフを描くように,x1, y1とx2, y2の二つのペアのリストを与え(x1, x2は時間のリスト,y1, y2はデータ),
x_intersect, y_intersect = intersection(x1, y1, x2, y2)とすることで,交点を計算できる.x_intersectには交点の時間(x軸),y_intersectには交点の座標(y軸)のリストが格納される.
ここでは,速度カーブと,y=0の直線の交点を求めたいので,たとえば,velに速度データのリストと,timeに相当する時間のリストを与え,
intersection(time, vel, time, np.zeros(len(vel)))を計算することで,交差する点を求められる.ここで2つの線(曲線と直線)は,
1.時間のリストtimeと,速度データvelから構成される曲線
2.timeと,ゼロのデータが並んだリストnp.zeros(len(vel))のy=0の直線
を表している.
前述のように,intersection()関数は,交点のx座標(ここでは時間)と,y座標を返してくれるので,
time, y = intersection(time, vel, time, np.zeros(len(vel)))として,速度曲線とy=0が交差する点から,マーカの位置の座標が極大値となる時間が計算で,周期の計算ができる.図10には,このようにして計算した,板のマーカの一つのx座標の一階微分(速度)が0と交差する点をプロットした.

同じ計算を,あまり安定していない振動で計算すると,図11のようになる.

図11のグラフでは極大値の時間間隔が一定でないことがわかる.このような,回転中心が一定でない振動から算出した慣性モーメントと,比較的安定した振動から算出した慣性モーメントを比較すると,明らかに異なるので,ここでは,安定した振動だけ使用して,慣性モーメントを計算した.安定の判別は,図10, 11の時間間隔の標準偏差で判断する.

10試技計測し,振動が安定していると(標準偏差が小),振動周期$${T}$$も一定の値に近づくことがわかる(図12).そこで,ここでは標準偏差が0.05以下の試技だけ計算に利用する.
このように,回転の中心が一定しないなど,振動が安定しない試技は除外するとよいだろう.
ここで,強調しておきたいことは,周期$${T}の2乗を利用するので,周期の精度に敏感で,わずか小数点以下3桁目で,精度が大きく左右されるということである.この精度を得るためには,ストップウォッチでは難しく,かつ上記のような慎重な計算が必要となることを示している.
10回計測し,そのうち安定していた6試技から計算したNPBボールの慣性モーメントは$${[6.96, 7.17, 6.89, 6.79, 6.96, 7.01] \times 10^{-5} ~[\mathrm{kg ~m}^2]}$$で,平均値は$${6.96 \times10^{-5} (= 0.0000696) ~[\mathrm{kg ~m}^2]}$$であった.図12の右側に位置している振動データ(これでも,結構注意深く回しているつもりであったが...)では$${[6.3, 6.5, 6.6, 7.5] \times 10^{-5} ~[\mathrm{kg ~m}^2]}$$ぐらいになる.
ここで参考値として,
$$
l = 0.1425 [\mathrm{m}] \\
a= 1.1540 [\mathrm{m}]\\
m_{plate} = 0.0615 [\mathrm{kg}]\\
m_{npb} = 0.1489 [\mathrm{kg}]
$$
である.なお,$${m_{plate}, m_{npb}}$$は板とNPB公式ボールの質量である.
この値は,慣性モーメント計測装置で計測した値と近い値を示しており,この程度,努力することで,真値に近づけることができそうだ.
なお,ここで示した計測データはすべてボール+板の慣性モーメントの計測によるもので,板単独の慣性モーメントの計測も同様に行って,差分でボールの慣性モーメントを計測している.
JABAボールの慣性モーメント
同じ方法で計測した,JABA(日本野球連盟)公式ボールの慣性モーメントは,$${6.81 \times10^{-5} (= 0.0000681) ~[\mathrm{kg ~m}^2]}$$であった.ボールの個体差や,ボールの種類による実際の違いがどのぐらいあるかは,いまのところわからない.社会人野球の公式ボールの慣性モーメントが,NPBボールより小さくなるように作られているかは興味深いところである.
ここで,使用したJABAの硬式ボールの質量は $${0.1484 [\mathrm{kg}]}$$であった.
ボールによる違いは,振動周期とボールの質量である.平均のNPBボールの振動周期もJABAボールの振動周期も0.811 [s]で違いは少なかった.違いは質量だけである.
計算上,この違いは,質量の違いだけが反映されているが,このあたりはもはや誤差内だろう.JABAとNPBボールの違いがないとすると,おおよそ,$${(6.90 \pm 0.20) \times10^{-5} ~[\mathrm{kg ~m}^2]}$$ぐらいと考えておくのが良いだろう.
もし,大学の工学部などに慣性モーメント計測装置などがあれば,ぜひ測っていただき,教えていただけると幸いである.
補足
補足1:単振り子の運動方程式
以下の証明では,下記の事前知識を使用することになる.
単振り子の微分方程式は,二階の斉次(同次)線形微分方程式で
$$
\ddot{\psi} + \frac{g}{l} \psi = 0
$$
と書くことができる.
ここで,斉次(同次)とは変数$${\psi}$$に関する項は全て左辺に書くことができ,右辺が$${0}$$となることを指す.もし,$${\psi}$$の項を含まない項が存在すれば,それは非斉次(同次)となる.
ここで,この式のパラメータ($${\frac{g}{l}}$$)を簡単にするため,
$$
\omega^2 = \frac{g}{l}
\\
\ddot{\psi} + \omega^2 \psi = 0
$$
のように置き換える.また,この二階斉次線形微分方程式をなぜ以下のように解くかを考えず(問わず)に,
$$
\psi (t)= e^{ct}
$$
と置く(これは先験的な知識を利用しているからである).ここで$${c}$$は定数である.すると,
$$
\dot{\psi} (t)= c e^{ct}, ~~\ddot{\psi} (t)= c^2 e^{ct}
$$
となることが知られているので(証明は文献1などを参照),これを先程の二階斉次線形微分方程式に代入すると,
$$
\ddot{\psi} + \omega^2 \psi = 0
\\
c^2 e^{ct} + \omega^2 e^{ct} = 0
\\
(c^2 + \omega^2) e^{ct} = 0
$$
となるので,これが成り立つために,
$$
c^2 = -\omega^2
$$
となるので,この2次方程式の解は実数解を持たず,
$$
c = \pm \omega i
$$
となり,虚数$${i}$$を含み,
$$
\psi_1 (t)= e^{\omega i t},~\psi_2 (t)= e^{-\omega i t}
$$
の2つが解となる.このままでは,どのような運動を行うかわからないので,オイラーの公式
$$
e^{ix} = \cos x + i \sin x
$$
を利用すると,
$$
\psi_1 (t)= e^{\omega i t} = \cos \omega t + i \sin \omega t\\
\psi_2 (t)= e^{-\omega i t} = \cos \omega t + i \sin (-\omega t)= \cos \omega t - i \sin \omega t
$$
となり,この2つの線形結合として一般解
$$
c_1 \psi_1 (t) + c_2 \psi_2 (t) = c_1(\cos \omega t + i \sin \omega t) + c_2 (\cos \omega t - i \sin \omega t)\\
= (c_1 + c_2) \cos \omega t + i(c_1 - c_2) \sin \omega t
$$
が得られる.これは複素数であるが,$${\psi}$$は振り子の角度を表すので実数となってほしい.つまり$${c_1 + c_2}$$と$${i(c_1 - c_2)}$$がともに実数となるためには,$${c_1, c_2}$$が互いに共役な複素数となる必要があり,たとえば
$$
c_1 = A + i B
\\
c_2 = A - iB
$$
とすると,$${\psi}$$の解は
$$
\psi (t) = 2A \cos \omega t - 2B \sin \omega t
$$
が一般解となり,さらに$${2A=a \cos \alpha, 2B = a \sin \alpha}$$と置けば,
$$
\psi (t) = a \cos (\omega t + \alpha)
\\
= a \cos \left( \sqrt{\frac{g}{l}} t + \alpha\right)
$$
を得る.ここで,$${\omega}$$は角振動数(angular frequency)と呼ばれる.
解答例:ボールの慣性モーメント
例題の表から,それぞれの板と,板+ボールの周期$${T_p, T_{pb}}$$は
$$
T_p = 2.144 [\text{s}]\\
T_{pb} = 1.243 [\text{s}]
$$
となる.そこで,物体の質量を$${m}$$,糸の長さ$${a}$$,回転中心と糸までの距離$${l}$$,周期$${T}$$とすると
def inertia_moment(m, a, l, T):
grav = 9.8
return m * grav * l**2 * T**2 / (4 * np.pi**2 * a)で計算でき,
mp=.06
a=1.76
l=.142
Tp=2.144
inertia_moment(mp, a, l, Tp)
>>> 0.000784388417905868mpb=.06+.145
a=1.76
l=.142
Tpb=1.243
inertia_moment(mpb, a, l, Tpb)
>>> 0.0009007960606645453のように,板の慣性モーメント$${I_p}$$は0.000784 [kg m$${^2}$$],板+ボールの慣性モーエント$${I_p + I_b}$$は0.000901 [kg m$${^2}$$]となり,ボールの慣性モーメント$${I_b}$$は0.00012 [kg m$${^2}$$]となる.
参考文献
1)R. F. Chandler et al.,Investigation of Inertial Properties of the Human Body , 1974



【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
【データの計測について】
スポーツセンシング社のスタジオで,フォースプレートやモーションキャプチャを利用した計測も行えます.出力されるデータと,ここで示したプログラム(入力データの取り込み関数を少々改変する必要があるが)で,同様な解析を行えますので,まずはお気軽にお問い合わせください.
