
動かして学ぶバイオメカニクス#10 〜角速度ベクトル〜
オイラーの運動方程式の計算においては,前回の姿勢角度行列から角速度ベクトルを計算し,慣性モーメントとその角速度ベクトルから慣性力を計算することになる.角速度ベクトルの計算自体は簡単であるが,ここではその幾何学的意味を考える.
角速度ベクトルの計算
角速度ベクトルの意味と導出は,
の補足2で述べたので,そちらを参照していただきたい.簡単におさらいすると,回転行列$${\bm{R}}$$は,直交行列であるため,
$$
\bm{R}^T = \bm{R}^{-1}
$$
を満たし,
$$
\bm{RR}^T = \bm{R}^T \bm{R} = \bm{E}
$$
が成り立つため($${\bm{E}}$$は単位ベクトル),これを時間微分し,
$$
\begin{aligned}
\dot{\bm{R}} \bm{R}^T + \bm{R} \dot{\bm{R}}^T &= \bm{0}
\\
\dot{\bm{R}} \bm{R}^T = -\bm{R} \dot{\bm{R}}^T
\\
\dot{\bm{R}} = -(\bm{R} \dot{\bm{R}}^T) \bm{R}
\\
\dot{\bm{R}} = [\bm{\omega} \times] \bm{R}
\end{aligned}
$$
より,
$$
\bm{\Omega} \equiv [\bm{\omega} \times ] =
\begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{bmatrix}
= -\dot{\bm{R}} \bm{R}^T
$$
を得る.ここで,行列$${\bm{\Omega}}$$は歪対称行列(わいたいしょうぎょうれつ),またはひずみ対称行列(skew symmetric matrix)と呼ばれ,この行列を転置すると,行列の要素の符号が反転し,
$$
\bm{\Omega}^T = -\bm{\Omega}
$$
を満たす.そして,これまで何度も利用してきたように,ベクトルの外積の計算はこの歪対称行列を利用して
$$
\bm{\omega} \times \bm{r} =
\begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{bmatrix} \begin{bmatrix} r_x \\ r_y \\ r_z \end{bmatrix} = [\bm{\omega} \times ] \bm{r} = \bm{\Omega} \bm{r}
$$
のように書くことができる.すなわち3次元ベクトル$${\bm{\omega}}$$から歪対称行列$${\bm{\Omega}}$$を作る操作を
$$
[\bm{\omega} \times]
$$
と記述することで($${\tilde{\bm{\omega}}}$$などのように記述することも多い),ベクトルの外積が行列演算で計算できるため多くのメリットがある.ただし,その必要もなく(たとえば格好が良いからという不純な動機で)不用意に歪対称行列で記述するのは式をわかりにくくするので注意されたい.
このように,外積は$${[\bm{\omega} \times ]}$$という操作(記号)で歪対称行列に書き換えることができるが,反対に歪対称行列から,3次元ベクトル(この場合,角速度ベクトル)を抽出する操作を,記号$${\vee}$$(ヴィー)を用いて,次のように与える(文献1).このとき注意したいことは,後ほど述べるが,各角速度成分は行列内に二つ現れることに注意されたい.
$$
\begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{bmatrix}^{\vee} = \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} \\
\bm{\Omega}^{\vee} = \bm{\omega}
$$
以上をまとめ,
$$
\bm{\Omega} = [\bm{\omega} \times ] =-\bm{R} \dot{\bm{R}}^T= \dot{\bm{R}} \bm{R}^T\\
\bm{\omega} = (-\bm{R} \dot{\bm{R}}^T)^{\vee} = (\dot{\bm{R}} \bm{R}^T)^{\vee}
$$
のように角速度に関する演算をまとめることができる.
角速度ベクトルの幾何学的意味
ここでは,具体的に$${\dot{\bm{R}} \bm{R}^T}$$をそれを構成する単位ベクトルレベルで眺めながら,その幾何学的意味を考えていく.
で述べたように,
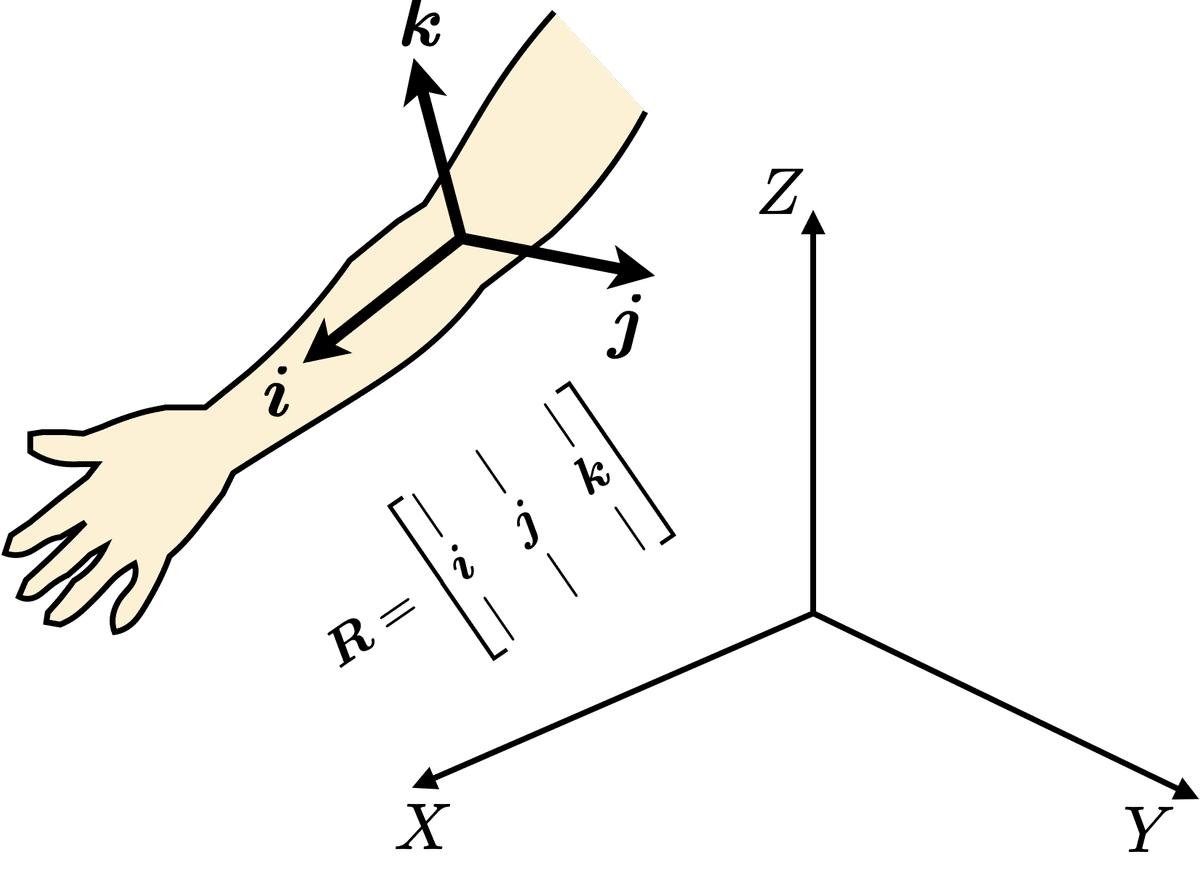
姿勢回転行列$${\bm{R}}$$は,身体に固定された直交(デカルト,カーテシアン)座標系の座標軸に張り付いた単位ベクトル$${\bm{i}, \bm{j}, \bm{k}}$$を並べたもの
$$
\bm{R} = [\bm{i}~ \bm{j}~ \bm{k}]
$$
である.ここで,これらのベクトルは
$$
\bm{i} = \begin{bmatrix} i_x \\ i_y \\ i_z \end{bmatrix}, \bm{j} = \begin{bmatrix} j_x \\ j_y \\ j_z \end{bmatrix}, \bm{k} = \begin{bmatrix} k_x \\ k_y \\ k_z \end{bmatrix}
$$
の縦ベクトルで記述する.
すると,この時間微分は$${\dot{\bm{R}}}$$は,これらの単位ベクトルの時間微分
$$
\dot{\bm{R}} = [\dot{\bm{i}}~ \dot{\bm{j}}~ \dot{\bm{k}}]
$$
で表され,角速度ベクトルの外積を表す歪対称行列$${\bm{\Omega}}$$は,
$$
\bm{\Omega} = [\bm{\omega} \times] = -\dot{\bm{R}} \bm{R}^T = -[\dot{\bm{i}}~ \dot{\bm{j}}~ \dot{\bm{k}}]\begin{bmatrix} \bm{i}^T\\ \bm{j}^T\\ \bm{k}^T \end{bmatrix} \\
= -\begin{bmatrix} \dot{i}_x & \dot{j}_x & \dot{k}_x \\ \dot{i}_y & \dot{j}_y & \dot{k}_y \\ \dot{i}_z & \dot{j}_z & \dot{k}_z \end{bmatrix}
\begin{bmatrix} i_x & i_y & i_z \\ j_x & j_y & j_z \\ k_x & k_y & k_z\end{bmatrix} \\
$$
のように,単位ベクトルの速度を並べた行列と,姿勢回転行列の転置との積で記述される.これは,絶対座標系$${XYZ}$$で記述した角速度ベクトル$${\bm{\omega}}$$に相当する.
ここで式が長くなるので,最後の式の展開は省略するが,対角成分は
$$
\dot{i}_x i_x + \dot{i}_y i_y + \dot{i}_z i_z = 0 \\
\dot{j}_x j_x + \dot{j}_y j_y + \dot{j}_z j_z = 0 \\
\dot{k}_x k_x + \dot{k}_y k_y + \dot{k}_z k_z = 0
$$
となる.これは,単位ベクトルの速度と同じ単位ベクトルとの内積で,回転運動をしている際には単位ベクトルとその速度が直交するためで,$${\bm{\Omega}}$$が歪対称行列である性質と一致する.
単位ベクトルの微分
姿勢回転行列が単位ベクトルを並べたものであることを考慮すると,姿勢回転行列の微分は次のように書き換えることができる.
$$
\dot{\bm{R}} = [\bm{\omega} \times ] \bm{R} \\
\frac{d}{dt} \left[\bm{i} ~~ \bm{j} ~~ \bm{k} \right] = [\bm{\omega} \times] \left[\bm{i} ~~ \bm{j} ~~ \bm{k} \right]\\
[\dot{\bm{i}}~~\dot{\bm{j}}~~\dot{\bm{k}}] = [\bm{\omega} \times \bm{i}~~~ \bm{\omega} \times \bm{j} ~~~ \bm{\omega} \times \bm{k} ]
$$
この関係を図2に示した(文献2).

身体に固定されたローカル座標系から見た角速度
次に,物体に固定されたローカル座標系$${xyz}$$から眺める角速度ベクトルを考える.
一般に,物体(身体)に固定されたモーションキャプチャのマーカを利用して角速度を計測する場合は,直接的にはこのローカル座標系における角速度を算出することになるだろう.
また,モーションセンサで計測する角速度も,ローカル座標系から見た角速度を計測する.
歪対称行列の座標変換
まず,角速度の歪対称行列$${\bm{\Omega} = [\bm{\omega} \times]}$$のローカル座標への座標変換$${\hat{\bm{\Omega}} = [(\bm{R}^T \bm{\omega}) \times]}$$を考える.いま考えようとしているのは,角速度ベクトル$${\bm{\omega}}$$のローカル座標系への変換$${\bm{R}^T\bm{\omega}}$$ではなく,歪対称行列の座標変換であることに注意されたい.
このことを考えやすくするため,$${\bm{\omega} \times \bm{p}}$$の座標変換$${\bm{R}^T (\bm{\omega} \times \bm{p})}$$を考えると,
$$
\begin{aligned}
\bm{R}^T (\bm{\omega} \times \bm{p}) &= (\bm{R}^T\bm{\omega}) \times (\bm{R}^T \bm{p})
\\
&=
[(\bm{R}^T\bm{\omega}) \times] (\bm{R}^T \bm{p})
\end{aligned}
$$
となる.一方,単位行列を$${\bm{E}}$$とし,$${\bm{RR}^T = \bm{E}}$$なので,
$$
\begin{aligned}
\bm{R}^T (\bm{\omega} \times \bm{p}) &= \bm{R}^T ([\bm{\omega} \times] \bm{p})
\\
&= \bm{R}^T [\bm{\omega} \times] \bm{p}
\\
&=( \bm{R}^T [\bm{\omega} \times]) \bm{p}
\\
&=( \bm{R}^T [\bm{\omega} \times]) (\bm{RR}^T\bm{p})
\\
&=(\bm{R}^T [\bm{\omega} \times]\bm{R}) (\bm{R}^T\bm{p})
\end{aligned}
$$
と計算できる.そこで,この2つの結果を見比べれば,角速度の歪対称行列$${\bm{\Omega} = [\bm{\omega} \times]}$$のローカル座標への座標変換
$$
\hat{\bm{\Omega}} = [(\bm{R}^T\bm{\omega}) \times] = \bm{R}^T [\bm{\omega} \times]\bm{R}
$$
を得る.
さらに,$${\bm{\Omega} = [\bm{\omega} \times] = -\bm{R} \dot{\bm{R}}^T}$$を代入すると,
$$
\begin{aligned}
\hat{\bm{\Omega}} &= \bm{R}^T [\bm{\omega} \times]\bm{R}
\\
&= \bm{R}^T(-\bm{R} \dot{\bm{R}}^T)\bm{R}
\\
&= -\dot{\bm{R}}^T\bm{R}
\end{aligned}
$$
を得る.
そこで,ローカル座標系で見た歪対称行列$${\hat{\bm{\Omega}}}$$は
$$
\hat{\bm{\Omega}} %=[\hat{\bm{\omega}} \times]=
%-\dot{\hat{\bm{R}}} \hat{\bm{R}}^T
=-\dot{\bm{R}}^T\bm{R}
= -\begin{bmatrix} \dot{\bm{i}}^T\\ \dot{\bm{j}}^T\\ \dot{\bm{k}}^T \end{bmatrix}[\bm{i}~\bm{j}~\bm{k}]=
-\begin{bmatrix} \dot{\bm{i}}^T \bm{i} & \dot{\bm{i}}^T \bm{j} & \dot{\bm{i}}^T \bm{k} \\ \dot{\bm{j}}^T \bm{i} & \dot{\bm{j}}^T \bm{j} & \dot{\bm{j}}^T \bm{k} \\ \dot{\bm{k}}^T \bm{i} & \dot{\bm{k}}^T \bm{j} & \dot{\bm{k}}^T \bm{k} \end{bmatrix}
$$
となる.ここで,ローカル座標形から見た角速度$${\hat{\bm{\omega}} = [\hat{\omega}_x~\hat{\omega}_y~\hat{\omega}_z]^T}$$で回転運動を行っている際,各単位ベクトルの速度と同じ単位ベクトルとの内積は直交するので,
$$
\dot{\bm{i}}^T \bm{i} = \dot{\bm{j}}^T \bm{j} = \dot{\bm{k}}^T \bm{k} = 0
$$
となるので,やはりここでも$${\hat{\bm{\Omega}} =[\hat{\bm{\omega}} \times]}$$の対角成分は$${0}$$となり,
$$
\hat{\bm{\Omega}} =[\hat{\bm{\omega}} \times]=
-\begin{bmatrix} 0 & \dot{\bm{i}}^T \bm{j} & \dot{\bm{i}}^T \bm{k} \\ \dot{\bm{j}}^T \bm{i} & 0 & \dot{\bm{j}}^T \bm{k} \\ \dot{\bm{k}}^T \bm{i} & \dot{\bm{k}}^T \bm{j} & 0 \end{bmatrix} =
\begin{bmatrix} 0 & -\hat{\omega}_z &\hat{\omega}_y \\ \hat{\omega}_z & 0 & -\hat{\omega}_x \\ -\hat{\omega}_y & \hat{\omega}_x & 0 \end{bmatrix}
$$
を得る.
ローカル座標形から見た角速度
これより,身体各部位に固定されたローカル座標形で記述した角速度ベクトル
$$
\hat{\bm{\omega}} = \hat{\bm{\Omega}}^{\vee} = \begin{bmatrix} \hat{\omega}_x \\ \hat{\omega}_y \\ \hat{\omega}_z \end{bmatrix}
=
\begin{bmatrix} \dot{\bm{j}}^T \bm{k} \\ \dot{\bm{k}}^T \bm{i} \\ \dot{\bm{i}}^T \bm{j} \end{bmatrix}
=
-\begin{bmatrix} \dot{\bm{k}}^T \bm{j} \\ \dot{\bm{i}}^T \bm{k} \\ \dot{\bm{j}}^T \bm{i} \end{bmatrix}
$$
を得る.先にも述べたが,この式は2種類の角速度の計算方法があることを示している.各単位ベクトルの直交性が保たれ,そのノルムが$${1}$$であれば,同じ数値計算結果となるので,どちらを使用しても良い.
そこで,この式の幾何学的意味を考える.

ここで,座標系が$${x}$$軸まわりに右ねじの方向に角速度$${\hat{\omega}_x}$$で回転しているとしよう(図3).すると,単位ベクトルの速度$${\dot{\bm{j}}, \dot{\bm{k}}}$$は$${yz}$$平面内を運動し,この回転によって単位ベクトル$${\dot{\bm{j}}}$$の微分は$${\bm{k}}$$方向を向き,単位ベクトル$${\dot{\bm{k}}}$$の微分は$${-\bm{j}}$$方向を向き,単位ベクトルの大きさが$${1}$$なので,角速度はそれらの内積で記述できることを示している.同様に$${\hat{\omega}_y, \hat{\omega}_z}$$についても成り立ち,これらは直交し独立に定まるので,$${xyz}$$成分を持つ一般の角速度ベクトルの計算でも成り立つ.
このように,角速度ベクトルは前章で算出する姿勢回転行列の微分,すなわち座標系に固定された単位ベクトルの微分を使用して計算される.
そこで,この後に述べるコードでは,この単位ベクトルの速度の性質を利用してローカル座標系の角速度ベクトル$${\hat{\bm{\omega}}}$$を計算する.
動かして学ぶ角速度ベクトルの計算
前章で記述したコードに,身体に固定されたローカル座標系の角速度ベクトルの計算を行う関数を加筆する.ここでは,新たに加えたその行列のインスタンス変数wに各部位の角速度ベクトルを代入する.
前章のコードからの修正・加筆箇所は少ないので,ここでは修正部分だけにフォーカスして説明する.角速度を計算するために必要なコードの全ては,これまで同様に,以下のGoogle Colaboratoryのリンクから,ブラウザでPythonコードを実行できるようにした.なお,ログインするためには,Googleアカウントが必要となるので注意をされたい.
また,使用するモーションキャプチャのサンプルデータ(sample_optitrack_221027.csv)は,このリンクからダウンロードして,Google Driveをマウントし,マウントしたドライブにそれらをコピーしてご使用いただきたい.これは,第6〜9章で使用したデータと同じであるので,すでにダウンロ度済みの方は,サイドダウンロードする必要はない.
クラスの定義
class BodyLink:
def __init__(self, l_id:int, name:str, m_type:str, mass_ratio:float, cg_ratio:float):
self.l_id = l_id # linkのID
self.name = name # linkの名前
self.m_type = m_type # マーカの種類(Bone, Bone Marker, Marker)(new9)
self.mass_ratio = mass_ratio # linkの質量分配比
self.cg_ratio = cg_ratio # linkの重心位置の分配比 (new6)
self.inertia_moment = None # linkの慣性モーメント (new8)
self.child_val = None # 子供の変数
self.sister_val = None # 兄弟姉妹の変数
self.distal_val = None # linkの遠位端の変数 (new6)
self.p = None # linkの関節の原点(近位端) (new8)
self.cg = None # linkの重心位置
self.acc = None # linkの重心の加速度
self.force = None # linkの関節に作用する力
self.rot = None # linkの姿勢行列 (new9)
self.w = None # linkのローカル座標系の角速度ベクトル (new10)クラスのインスタンス変数に角速度ベクトルwを追加する.ここに,後述の関数で姿勢回転行列rotから計算する,角速度ベクトルを代入する.
内積
Pythonには内積を計算する関数がnumpyに準備されているが,ベクトルの時系列データ(ここでは2次元配列を使用)に対する内積が準備されていないので,下記のようにdot_array()関数を定義する.
# (new10)
# 内積
# 時系列のベクトル(2次元配列)のa_arrayとb_arrayの「内積」を時系列(2次元配列)として出力
def dot_array(a_array, b_array):
return np.sum(a_array * b_array, axis=1)ローカル座標系の角速度ベクトル
# (new10)
# 単位ベクトルの速度と,直交する方向の単位ベクトルとの内積で計算
def angular_velocity(bases, weight, sf):
dot_bases = np.array([smoothing_spline(bases[i], weight, sf, order=1) for i in range(3)])
return np.array([dot_array(dot_bases[1], bases[2]),
dot_array(dot_bases[2], bases[0]),
dot_array(dot_bases[0], bases[1])]).T関数angular_velocity() は,前章で計算した,各部位に固定された姿勢回転行列のrotから,各身体部位に固定されたローカル座標系の角速度ベクトルwを計算する.
# (new10)
# b_inkと部位のl_idを指定し,各linkの姿勢行列(rot)から角速度を計算,格納
def set_w(b_link, l_id, weight=.0001, sf=360.):
av = angular_velocity(b_link[l_id].rot, weight, sf)
b_link[l_id].w = av
def set_w_link(b_link, l_id_list, weight=.0001, sf=360.):
for n in l_id_list:
set_w(b_link, n, weight, sf)関数set_w_link()によって,上記の関数angular_velocity() を使用して,次に示すように利用し,クラスBodyLinkのインスタンス変数wに格納する.
# 角速度をwに格納
set_w_link(b_link, range(1,16), weight=.0001, sf=360.)以上の計算で,例えば腰のローカル座標系における角速度ベクトルが次のように各速度ベクトルがwに格納されているはずである.
b_link[1].w
>>>
array([[ 0.06088865, 0.00547964, 0.01839272],
[ 0.06403957, 0.00131424, 0.01490732],
[ 0.06706201, -0.00266487, 0.01168945],
...,
[-0.06687528, -0.08669017, -0.10011528],
[-0.06939348, -0.08855914, -0.10294826],
[-0.07202398, -0.09056108, -0.10616355]])rotを使用して,これを絶対座標系の角速度ベクトルに変換することは,これまで述べたことを利用すれば容易であるが,それについては次章で述べることとする.
次章の予定
次章では,ここまで述べてきた慣性テンソル$${\bm{I}}$$と角速度ベクトル$${\bm{\omega}}$$を利用し,オイラーの運動方程式における慣性力項
$$
\bm{I} \dot{\bm{\omega}} + \bm{\omega} \times (\bm{I} \bm{\omega})
$$
の計算を行う.ヒトの運動にとっては,この項が大きくなることはエネルギー消費を増やすだけなので,特に床反力などの外力に近い部位では,実際のヒトの運動ではこの項を無視できるぐらい小さくしながら運動を行っている.この項を無視し運動方程式が静力学で記述できる場合が多いことに,意外と気がついていない方も多いのではないだろうか.
補足
オイラー角から角速度を計算することも可能であるが,オイラー角から角速度を計算することは考えないほうがよい.オイラー角は角度によって精度が異なることにもよるが,姿勢回転行列から直接角速度を計算できるのに,わざわざ,そこにオイラー角を媒介し計算することは余計な計算を増やし,計算精度を落とすだけである.
参考文献
1)ヒューマノイドロボット(改訂2版),梶田著,オーム社,2020
2)ロボットモーション(岩波講座 ロボット学2),内山・中村著,岩波書店,2004



【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
