
モーションにおける3次元回転 #4 〜オイラーの公式からロドリゲスの式へ〜
前章「モーションにおける3次元回転 #3」では,オイラーの公式を用いて2次元平面内の回転について説明した.
2次元と比べて3次元の回転運動の表現方法はかなり複雑である.この章では,3次元の回転行列のもう一つの表現方法である,ロドリゲスの式について説明する.クォータニオンはロドリゲスの式と密接に関係することから,ここでの目的は,これを学ぶことによって,次章(モーションにおける3次元回転 #5)で述べるクォータニオンの幾何学的意味をより深く理解することにある.
オイラーの定理
オイラーの定理は,
3次元において物体の回転を「ひとつの回転軸と回転角度で表すことができる」
ということを示している.
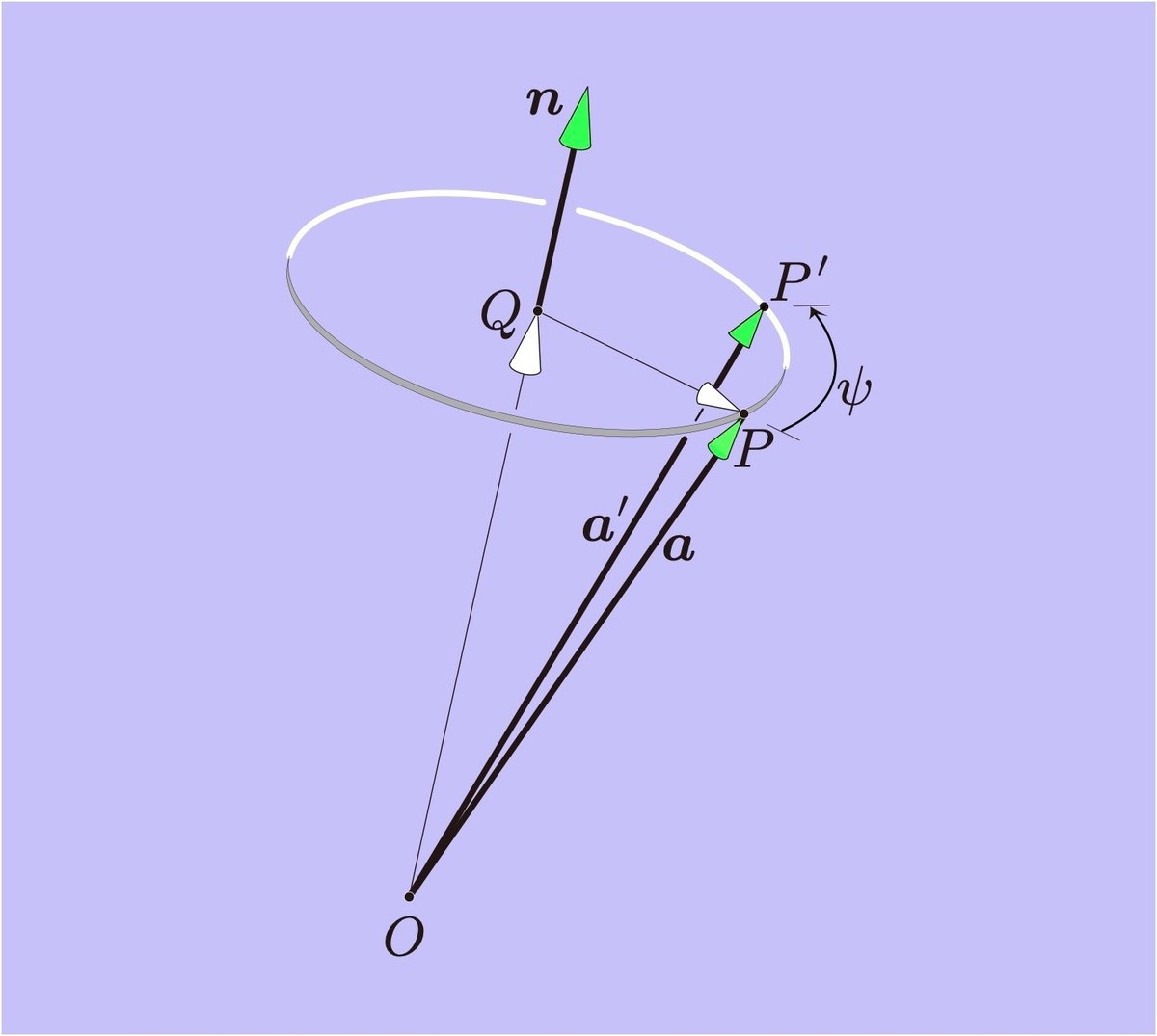
たとえば,任意のベクトル$${\bm{a}}$$を回転行列$${\bm{R}}$$によって回転させたベクトル$${\bm{a}'}$$は
$${\bm{Ra}=\bm{a}'}$$
と書くことができ,図1の点Pは回転$${\bm{R}}$$によって点P'に移動する.これに対して,唯一回転軸$${\bm{n}}$$に対しては
$${\bm{Rn}=\bm{n}}$$
が成り立ち,図1の点Qは同じ位置にとどまる.これは回転$${\bm{R}}$$によって「不変なベクトル」$${\bm{n}}$$が存在し,それが回転軸であることに相当する.
なお,$${\bm{n}}$$を単位ベクトルとし,
$${\bm{Rn}= \lambda \bm{n}}$$
で記述した直交行列$${\bm{R}}$$に対する固有値は,$${1, e^{i \psi}, e^{-i \psi}}$$で,このうちの1である固有値は,回転をこなっても不変を意味することから,唯一の回転軸の存在理由となっている.
ロドリゲスの式
物体の回転は,オイラーの定理から「ひとつの回転軸$${\bm{n}}$$と回転角度$${\psi}$$で表せる」ので,回転行列は
$${\bm{R} = \bm{E} + [\bm{n} \times ] \sin \psi + [\bm{n} \times ]^2(1- \cos \psi)}$$ (1)
のように表せる.これがロドリゲスの式(Rodrigues formula)として知られている.ここで,$${\bm{E}}$$は$${3\times3}$$の単位行列,$${[\bm{n} \times]}$$は外積を表す歪対称行列である(次節参照).この式の導出については最後に示す.
ロドリゲスの式は幾何学条件を使用し,他にも多様な表現が可能だが,ここではこの式の幾何学的意味を考える.その前に,外積と歪対称行列について次で説明を行う.
外積
ベクトル $${\bm{a}}$$と$${\bm{b}}$$の外積(outer product)はベクトルであることから$${\bm{a} \times \bm{b}}$$ベクトル積(vector product)とも呼ばれるが,一般に記号で$${\bm{a} \times \bm{b}}$$のように表現されるためクロス積(cross product)とも呼ばれる.
ベクトル $${\bm{a}}$$と$${\bm{b}}$$の外積(outer product)$${\bm{a} \times \bm{b}}$$は,図2のように,2つのベクトル$${\bm{a}, \bm{b}}$$に対して垂直な方向のベクトルを定める.

具体的な外積$${\bm{a} \times \bm{b}}$$の幾何学的性質は
1. $${\bm{a}, \bm{b}}$$の両方に直交し,始点を一致させて$${\bm{a}}$$を$${\bm{b}}$$に近づけるように,右ネジを回す際の進行方向を向く.
2. その大きさは,$${\bm{a}, \bm{b}}$$の始点を一致させて作る平行四辺形の面積($${|\bm{a}||\bm{b}|\sin\psi}$$)に等しい.
また,2つのベクトル
$${\bm{a}=\begin{bmatrix}a_x\\a_y\\a_z\end{bmatrix}, \bm{b}=\begin{bmatrix}b_x\\b_y\\b_z\end{bmatrix}}$$
に対して,外積の成分を
$${\bm{a} \times \bm{b}=\begin{bmatrix}a_y b_z - a_z b_y\\a_z b_x - a_x b_z\\a_x b_y - a_y b_x\end{bmatrix}}$$
のように書くことができる.
歪対称行列を使用した外積表現
$${\bm{n}=[n_x~n_y~n_z]^T}$$に対して,先に述べた$${[\bm{n} \times]}$$は以下のように定義される行列
$${[\bm{n} \times] \equiv \begin{bmatrix}0&-n_z&n_y\\n_z&0&-n_x\\-n_y&n_x&0\end{bmatrix}}$$
である.このような$${\bm{A}^T = -\bm{A}}$$の関係を満たす行列を歪対称行列,または交代行列と呼ぶ.これによって,ベクトルの外積を
$${\bm{c}=\bm{a}\times\bm{b}=[\bm{a}\times]\bm{b}\\\begin{bmatrix}c_x\\c_y\\c_z\end{bmatrix}=\begin{bmatrix}a_y b_z - a_z b_y\\a_z b_x - a_x b_z\\a_x b_y - a_y b_x\end{bmatrix}=\begin{bmatrix}0&-a_z&a_y\\a_z&0&-a_x\\-a_y&a_x&0\end{bmatrix}\begin{bmatrix}b_x\\b_y\\b_z\end{bmatrix}}$$
のように書くことができる.このような外積計算の行列による表現は,外積計算を含んだ式も線形表現できるので,今後多用することになる.
ロドリゲスの式の行列表現
ここで,ひとつ注意点を述べると,回転行列はオイラー角でも,単位クォータニオン(オイラーパラメータ)などで表現されうことが多いが,ロドリゲスの式でも回転行列を表現できることである.すなわち回転軸を意味する単位ベクトル$${\bm{n}}$$の3変数と回転角度$${\psi}$$でも,回転行列を表現できることを示している.これはクォータニオンの性質と似ているのだがその意味は,次の章で説明する.
式(1)を展開すると,
$${\bm{R}_{\bm{n}}(\psi) =\\ \hspace{5mm}\left[\begin{array}{cc}\cos\psi + n_x^2(1-\cos\psi) & n_x n_y(1-\cos\psi)-n_z \sin \psi \\ n_y n_x(1-\cos\psi)+ n_z \sin \psi & \cos\psi + n_y^2(1-\cos\psi) \\ n_z n_x(1-\cos\psi) - n_y \sin \psi & n_z n_y(1-\cos\psi) + n_x \sin \psi \end{array}\right.\\ ~\\ \hspace{6cm} \left.\begin{array} {c}n_x n_z(1-\cos\psi) + n_y \sin \psi\\ n_y n_z(1-\cos\psi) - n_x \sin \psi\\ \cos\psi + n_z^2(1-\cos\psi)\end{array}\right]}$$
となる.ここで,回転軸の単位ベクトル$${\bm{n}}$$の成分を
$${\bm{n}=\begin{bmatrix}n_x\\n_y\\n_z\end{bmatrix}}$$
とした.
ロドリゲスの式の逆変換
逆に,回転行列が既知のときに回転軸$${\bm{n}}$$と,回転角度$${\psi}$$も計算可能である.解析では回転行列を定めてから回転軸と回転角度を知りたいというこちらのニーズのほうが高いかもしれない.
前述の直交行列の固有値が1の場合を考えると,それに対応する固有ベクトルは回転軸に相当することを述べた.その時の固有ベクトル,すなわち回転軸を$${\bm{w}=[w_1~w_2~w_3]^T}$$とすると,
$$
\bm{R} \bm{w} = \bm{w}
$$
が成立する.また,$${\bm{R}}$$は直交行列なので,$${\bm{R}^T = \bm{R}^{-1}}$$が成立し,両辺に$${\bm{R}^T}$$を掛けて
$$
\bm{R}^T \bm{R} \bm{w} = \bm{R}^T\bm{w} \\ \bm{w} = \bm{R}^T\bm{w}
$$
となるので,
$$
(\bm{R} - \bm{R}^T)\bm{w} = \bm{0}
$$
を得る.また,回転行列$${\bm{R}}$$が以下のように既知のとき,
$${\bm{R}=\begin{bmatrix}r_{11}&r_{12}&r_{13}\\ r_{21}&r_{22}&r_{23}\\ r_{31}&r_{32}&r_{33}\end{bmatrix}}$$
とすると,
$$
(\bm{R} - \bm{R}^T)\bm{w} = \bm{0} \\ \begin{bmatrix}0 & r_{12}-r_{21} &r_{13} - r_{31}\\ r_{21} - r_{12} & 0 & r_{23} - r_{32} \\ r_{31}-r_{13} & r_{32}-r_{23} & 0\end{bmatrix} \begin{bmatrix}w_1\\w_2\\w_3\end{bmatrix}= \begin{bmatrix}0\\0\\0 \end{bmatrix}
$$
となるが,$${\bm{R} - \bm{R}^T}$$は歪対称行列となっていることに気がつく.そこで,これをベクトル$${\bm{W} }$$で記述された$${[\bm{W} \times]}$$と書くと,これは外積の演算を意味するので,
$$
\bm{W} \equiv \begin{bmatrix} r_{32}-r_{23} \\ r_{13} - r_{31} \\ r_{21} - r_{12}\end{bmatrix} \\ \bm{R} - \bm{R}^T = \begin{bmatrix}0 & r_{12}-r_{21} &r_{13} - r_{31}\\ r_{21} - r_{12} & 0 & r_{23} - r_{32} \\ r_{31}-r_{13} & r_{32}-r_{23} & 0\end{bmatrix}=[\bm{W} \times]
$$
と書け,$${\bm{W} \times \bm{w} = \bm{0}}$$を満たす$${\bm{w}}$$は,外積の幾何学的意味からも
$$
\bm{w} = \bm{W}
$$
しかない.そこで,ベクトル$${\bm{w}}$$を
$${\bm{w}\equiv\begin{bmatrix}r_{32} - r_{23}\\ r_{13} - r_{31} \\ r_{21}-n_{12}\end{bmatrix}}$$
と定義すると,大きさが1の回転軸$${\bm{n}}$$は
$${\bm{n}=\frac{\bm{w}}{||\bm{w}||}}$$
のようにベクトル$${\bm{w}}$$の単位ベクトルとなり,回転角度$${\psi}$$は
$${\psi = \mathrm{atan2} (\sin \psi, \cos \psi)}$$
となる.ただし,ここで
$${\cos \psi = \frac{1}{2}(\mathrm{tr}~ \bm{R} - 1)\\ = \frac{1}{2}(n_{11} + n_{22} + n_{33}-1)}$$
であり,$${\bm{n}, \cos \psi}$$が既知なので,$${\sin \psi}$$はロドリゲスの式$${\bm{R} = \bm{E} + [\bm{n} \times ] \sin \psi + [\bm{n} \times ]^2(1- \cos \psi)}$$から算出する.
また,トレース$${\rm{tr}~ \bm{R}}$$は,前述の行列$${\bm{R}}$$の対角要素の和
$${{\mathrm{tr}}~ \bm{R} = n_{11} + n_{22} + n_{33}}$$
である.
角度を計算する$${\rm{atan2} (y,x)}$$はプログラミング言語などの組み込み関数として広く使用されている2引数の逆正接関数($${\tan()}$$の逆関数)である.引数の順番が$${y,x}$$の順番であることに注意する.これを使用することで,角度が四象限にわたる符号も得られ,かつ計算精度も高い.
なお,PythonのNumpy場合のatan2()関数としては,np.arctan2(y, x)を使用する.これは引数が二つで,arctan(y / x)をラジアンで返す.この角度は,極座標平面において原点から座標(x, y)へのベクトルがx軸の正の方向となす角度(偏角)であり,戻り値は$${-\pi}$$から$${\pi}$$(-180度から180度)の間になる.計算言語によって,引数の順番,定義域に差があるので注意されたい.
読者は角度$${\psi}$$の計算は,$${\cos \psi = \frac{1}{2}(\rm{tr}~ \bm{R} - 1) }$$の逆関数で計算すれば良いと考えるかもしれないが,上記の符号と計算精度の理由から,上記のように計算が複雑化しても,原則$${\cos ^{-1}()}$$を角度計算では使用してはいけないことを留意しておくべきである.
ロドリゲスの式の導出
ベクトルの計算準備

ここでは,次節でロドリゲスの式の証明を行うための,射影と反射影というベクトルの幾何学的計算準備を行う.
ベクトル$${\bm{a}}$$はベクトル$${\bm{n}}$$に平行な成分$${\bm{a}_{||}}$$と,ベクトル$${\bm{n}}$$に対して直交する成分$${\bm{a}_{\perp}}$$とに分解することができるため,ベクトル$${\bm{a}}$$は
$${\bm{a} = \bm{a}_{||} + \bm{a}_{\perp}}$$ (2)
と書くことができ,$${\bm{a}_{||}}$$を$${\bm{a}}$$の$${\bm{n}}$$への射影(rejection),$${\bm{a}_{\perp}}$$を$${\bm{a}}$$の$${\bm{n}}$$からの反射影(rejection)とよぶ.
射影$${\bm{a}_{||}}$$の長さは,ベクトル$${\bm{a}, \bm{n}}$$の内積$${ \bm{a}^T \bm{n}}$$で計算できるので,射影$${\bm{a}_{||}}$$は
$${\bm{a}_{||}= (\bm{a}^T \bm{n})\bm{n} }$$
と書け,さらに
$${\bm{a}_{||} = (\bm{a}^T \bm{n})\bm{n}= (\bm{n}^T \bm{a})\bm{n}=\bm{n}(\bm{n}^T \bm{a})\\ = (\bm{n} \bm{n}^T) \bm{a}}$$
と書き換えることができる.ここで,内積は順序を入れ替えても良いというルールなどに基づいて書き換えている.
一方,反射影$${\bm{a}_{\perp}}$$は式(2)を利用して,
$${\bm{a}_{\perp} = \bm{a} - \bm{a}_{||}= \bm{a}- (\bm{n}^T \bm{n}) \bm{a} = (\bm{E} - \bm{n}^T \bm{n})\bm{a}}$$
と書くことができる.この射影と反射影を利用して,次にロドリゲスの式を幾何学的に導いていく.
ロドリゲスの式の幾何学的意味
この節では,ロドリゲスの式の幾何学的意味を理解するために,ロドリゲスの式の幾何学的な導出を行う.内積,外積,ベクトル三重積などの性質を使用して証明を試みるが,この節は読み飛ばしても構わない.

回転行列$${\bm{R}}$$にベクトル$${\bm{a}}$$をかけると,ベクトル$${\bm{a}}$$を角度$${\psi}$$だけ回転して$${\bm{a}'}$$となる.これを式で表すと,
$${ \bm{a}'=\bm{Ra} = \bm{a} + [\bm{n} \times ] \bm{a} \sin \psi + [\bm{n} \times ]^2 \bm{a}(1- \cos \psi)}$$ (2)
となる.そこで,図4におけるベクトル$${\bm{a}'}$$と,この式の関係について検証する.ベクトル$${\bm{a}'}$$は点P'を指し示している.点P'は,原点Oから,点P,Hを経由してP'に達するので
$${\bm{a}' = \overrightarrow{OP}' = \overrightarrow{OP}+\overrightarrow{PH}+\overrightarrow{HP'}}$$
と書くことができる.そこで,これを分解して考える.まず,円の半径は同じ長さであるので,
$${||\overrightarrow{QR}||=||\overrightarrow{QP'}||=||\overrightarrow{QP}||=||[\bm{n}\times] \bm{a}||=||\bm{a}_{\perp}||=||(\bm{E}-\bm{n}^T \bm{n})\bm{a}||}$$
が成り立つ.そして,まず,
1: $${\overrightarrow{OP}}$$はベクトル$${\bm{a}}$$
$${\overrightarrow{OP}=\bm{a}}$$
である.
2: $${\overrightarrow{PH}}$$は,$${\overrightarrow{PH}}$$の長さに$${\overrightarrow{PH}}$$方向の単位ベクトルをかけたものなので,
2-1: まず,長さ$${||\overrightarrow{PH}||}$$を求める.
$${||\overrightarrow{PH}||=||\overrightarrow{HP}||=||\overrightarrow{QP}-\overrightarrow{QH}||}$$であるため.
2-1-1: まず,$${\overrightarrow{QP}}$$を考えると,ベクトル$${\overrightarrow{QP}}$$は$${\bm{a}}$$の$${\bm{n}}$$からの反射影$${\bm{a}_{\perp}}$$であるため,前節の結果を利用し,$${\overrightarrow{QP}=\bm{a}_{\perp}= (\bm{E} - \bm{n}^T \bm{n})\bm{a}}$$を得る.
2-1-2: また,ベクトル$${\overrightarrow{QH}}$$は,$${\overrightarrow{QP’}}$$のベクトルの$${\overrightarrow{QP}=\bm{a}_{\perp}}$$への射影であるので
$${\overrightarrow{QH} = \cos \psi ||\overrightarrow{QP'}|| \frac{\overrightarrow{QP}}{||\overrightarrow{QP}||}= \cos \psi ||\overrightarrow{QP}|| \frac{\overrightarrow{QP}}{||\overrightarrow{QP}||}= \cos \psi ~\overrightarrow{QP} \\=\cos\psi ~\bm{a}_{\perp}=\cos \psi(\bm{E}-\bm{n}^T\bm{n}) \bm{a}}$$
となる.2-1-1と2-1-2の結果を合わせて,
$${||\overrightarrow{PH}|| =||\overrightarrow{QP}-\overrightarrow{QH}||\\=||\bm{a}_{\perp}-\cos \psi\bm{a}_{\perp}||\\=||(1-\cos \psi)\bm{a}_{\perp}||}$$
となる.以上から,$${\overrightarrow{PH}}$$は,長さ$${||\overrightarrow{PH}||}$$に$${\overrightarrow{PQ}}$$方向の単位ベクトルをかけたものなので,
$${\overrightarrow{PH} = -||(1-\cos \psi)\bm{a}_{\perp}|| ~\overrightarrow{QP} = -||(1-\cos \psi)\bm{a}_{\perp}|| ~\frac{\bm{a}_{\perp}}{||\bm{a}_{\perp}||}\\=-(1 - \cos \psi)\bm{a}_{\perp}= -(1 - \cos \psi)(\bm{E}-\bm{n}^T\bm{n}) \bm{a}}$$
を得る.
3: 最後に,ベクトル$${\overrightarrow{HP'}}$$は,長さ$${||\overrightarrow{HP'}||=||\overrightarrow{QP'}||\sin \psi = ||~[\bm{n}\times] \bm{a}~|| \sin \psi}$$に対して,$${\overrightarrow{HP'}}$$ の向きのベクトル $${[\bm{n}\times] \bm{a}}$$の単位ベクトル$${\frac{[\bm{n}\times] \bm{a}}{||~[\bm{n}\times] \bm{a}~||}}$$をかけたものであるので,
$${\overrightarrow{HP'}=||~[\bm{n}\times] \bm{a}~|| \sin \psi \frac{[\bm{n}\times] \bm{a}}{||~[\bm{n}\times] \bm{a}~||} = \sin \psi ~[\bm{n}\times] \bm{a}}$$
を得る.以上をまとめて,
$${\bm{a}' = \overrightarrow{OP}' = \overrightarrow{OP}+\overrightarrow{PH}+\overrightarrow{HP'}\\=\bm{a}-(1 - \cos \psi)(\bm{E}-\bm{n}^T\bm{n}) \bm{a}+\sin \psi ~[\bm{n}\times] \bm{a}}$$ (3)
を得る.
なお,ベクトルの三重積から
$${(\bm{c}\times \bm{b}) \bm{a} = ([\bm{c} \times ][\bm{b} \times ]) \bm{a} = (\bm{bc}^T )\bm{a} − (\bm{c}^T \bm{b})\bm{a}}$$
が成り立つが,ここで$${\bm{b}, \bm{c}}$$それぞれに$${\bm{n}}$$を代入すると,
$${([\bm{n} \times ][\bm{n} \times ])\bm{a} = (\bm{nn}^T )\bm{a} − \bm{Ea} = (\bm{nn}^T − \bm{E})\bm{a}}$$
となることを利用し,式(3)に代入すると,
$${\bm{a}' = \overrightarrow{OP}' = \overrightarrow{OP}+\overrightarrow{PH}+\overrightarrow{HP'}\\=\bm{a}+(1 - \cos \psi)([\bm{n} \times ][\bm{n} \times ]) \bm{a}+\sin \psi ~[\bm{n}\times] \bm{a}\\= \bm{a} + [\bm{n} \times ] \bm{a} \sin \psi + [\bm{n} \times ]^2 \bm{a}(1- \cos \psi)}$$
を得て,これは式(1)のロドリゲスの式と一致する.以上,ロドリゲスの式を幾何学的に導出した.
最後に
ロドリゲスの式の幾何学的意味を説明した.ここで重要なことは,この式は回転行列$${\bm{R}}$$を回転軸を示す単位ベクトル$${\bm{n}}$$と回転角度$${\psi}$$だけで表現でき,特にこの式(1)の形では,複素数で2次元の回転運動を記述するオイラーの公式を連想させる形式で書かれていることにある.
式(1)のベクトル$${\overrightarrow{OP}=\bm{a}}$$で平面に移動した後は,図4右の円で表される平面内の運動を考えればよく,この式は,なにやら$${[\bm{n}\times]}$$が複素数における虚数と似たような役割を果たしそうなことと,3次元の回転を表すクォータニオンが2次元の複素数の拡張になっている?ことを予感させてくれる.
次章で「ロドリゲスの式のもうひとつの幾何学的意味」について述べていく.



【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
