
動かして学ぶバイオメカニクス #24 〜キック動作の全身解析 1〜
身体運動の力学解析の全自動化を実現できないことはない.しかしフィルタリングの重み係数などの設定次第で解は大きく異り,パラメータ等の確認作業を省いてしまっては,安心した計算結果を得ることはできないだろう.ここでは,これまでのようにきれいに計算された結果だけを示すのではなく,その結果を出す試行錯誤の過程も含めて示していく.未知なるデータの完全な自動化は難しいが,工夫すればこれらの作業の省力化は可能なはずだ.
なお,これまでのクラスや関数定義をいちいち評価するのは面倒なので,ファイルにまとめ,それをimportする形で読み込む形式に変更した.
はじめに
これまで示してきたデータは,フィルタの重みの選択などの試行錯誤による調整を経た結果だけを示しているが,このように良い結果を得るために実際にはどろくさい作業が必要となることが多々ある.ここでは,その過程を示すことで,研究活動などでいかしていただければと思う.
また,解析対象としてあらたにアメリカンフットボールのキック動作を取り上げ,次回はバイオメカニクス的視点でデータを眺めていきたい.今回は,計測環境を整える(フィルタのパラメータなどを決定する)ところまで行う.
今回はキック動作を取り上げ,関数やその扱い方を変更した以外に,理論的な目新しさは少ない.しかし避けて通れないない過程をまとめておく.また図9,14に全身の角運動量の意味を図示し,最後に身体のダイナミクスからCOP(近似のないZMP)とあわせてアニメーションを示した.
確認した動作環境とコードについて
いつものように,以下のGoogle ColaboratoryのリンクからブラウザでPythonコードを実行できる.なお,ログインするためには,Googleアカウントが必要となるので注意をされたい.
なお,これまで定義してきたクラスと関数の定義は,ファイルbody_link.pyにまとめた.このファイル(body_link.py)と,使用するモーションキャプチャのサンプルデータ(sample_optitrack_sec24.csv)は,各リンクからダウンロードし,Colabを利用する場合はマウントしたGoogle Driveに,ご自身の環境で動かす場合はご自身の環境にそれらをコピーしてご使用いただきたい.
注意: ファイル"body_link.py"をクリックするとファイルの中身が表示されるが,右上のメニュー"︙"からさらにダウンロードしていただきたい.
ファイル"sample_optitrack_sec24.csv"は,ダウンロードしたファイルのファイル名が"sample_optitrack_sec24 - sample_optitrack_sec24.csv"と長くなる不具合が発生している.その場合,お手数だがファイル名を"sample_optitrack_sec24.csv”へ変更するなどの対応をお願いしたい.
また,サンプルデータの取り扱いについては,このページの最後の【サンプルデータについて】をご参照いただきたい.
関数などが定義されたファイルbody_link.pyをGoogle Colabで利用する場合,データをGoogle Driveにマウント後,例えば下記のように,sys.path.append()関数で
# Google Colabの場合(例)
python_lib_path = '/content/drive/MyDrive/.../lib'
sys.path.append(python_lib_path)
import body_link as blのようにファイルbody_link.pyを置いたパスを設定し,importでbody_link.pyファイルを読み込めばよい.Colabではなく,ご自身の環境下でのPythonをご利用する場合も,適宜上記のパス(python_lib_path)を設定していただきたい.なお,このファイルを利用するためにimportする際に,上記のようにbody_link.py のモジュールを bl という名前で読み込んでいる.そこで,このファイルに収められている,関数や変数は
bl.joint_vec()のようにbl.関数名,bl.変数名で使用することができる(body_link.pyには変数の定義は含まない).
また,Google ColaboratoryやGoogle Driveの使用方法は,
を参照されたい.
今回も含めて,貴重なデータの公開に同意していただいたアスリートの方々にも御礼を述べる.
データの確認
ここでは,力学解析を行う前に,以下の内容を確認する.
トリミング: 計測データの全てのフレーム(時間)を使うわけではない.また,全データを使用すると無駄な計算が増えてしまうため,事前にスティックピクチャを描くなどして,必要なフレームを抽出する.
フィルタリングのパラメータの選択: 適切なフィルタの係数の選択は実際のデータの状態で変化する.ここで使用している平滑化スプラインは,データの長さ,単位,暴れ具合などに依存するため,この作業は欠かせない.
接地時間の確認: ここではフォースプレート(FP)を使用しないので,解析で着地している足の判別と接地している時間(フレーム)情報が必要となる.ここでは,スティックピクチャと位置データなどから多角的に確認する.
全身の角運動量の計算方法の選択: 外力の力のモーメントを推定するが,この推定で全身の角運動量の時間微分を近似してよいかの確認を行う.詳細は第23章を参照されたい.
1.トリミング
まずは全フレームのデータを取り込み,スティックピクチャを下記コードで描き,解析するデータを抜き出す(トリミング)作業を行う.つまりトリミングするフレーム番号を同定する.
なお,スティックピクチャを描くアニメーションは,2種類のコードを示している.
1.スライダーバーによるインタラクティブなアニメーション
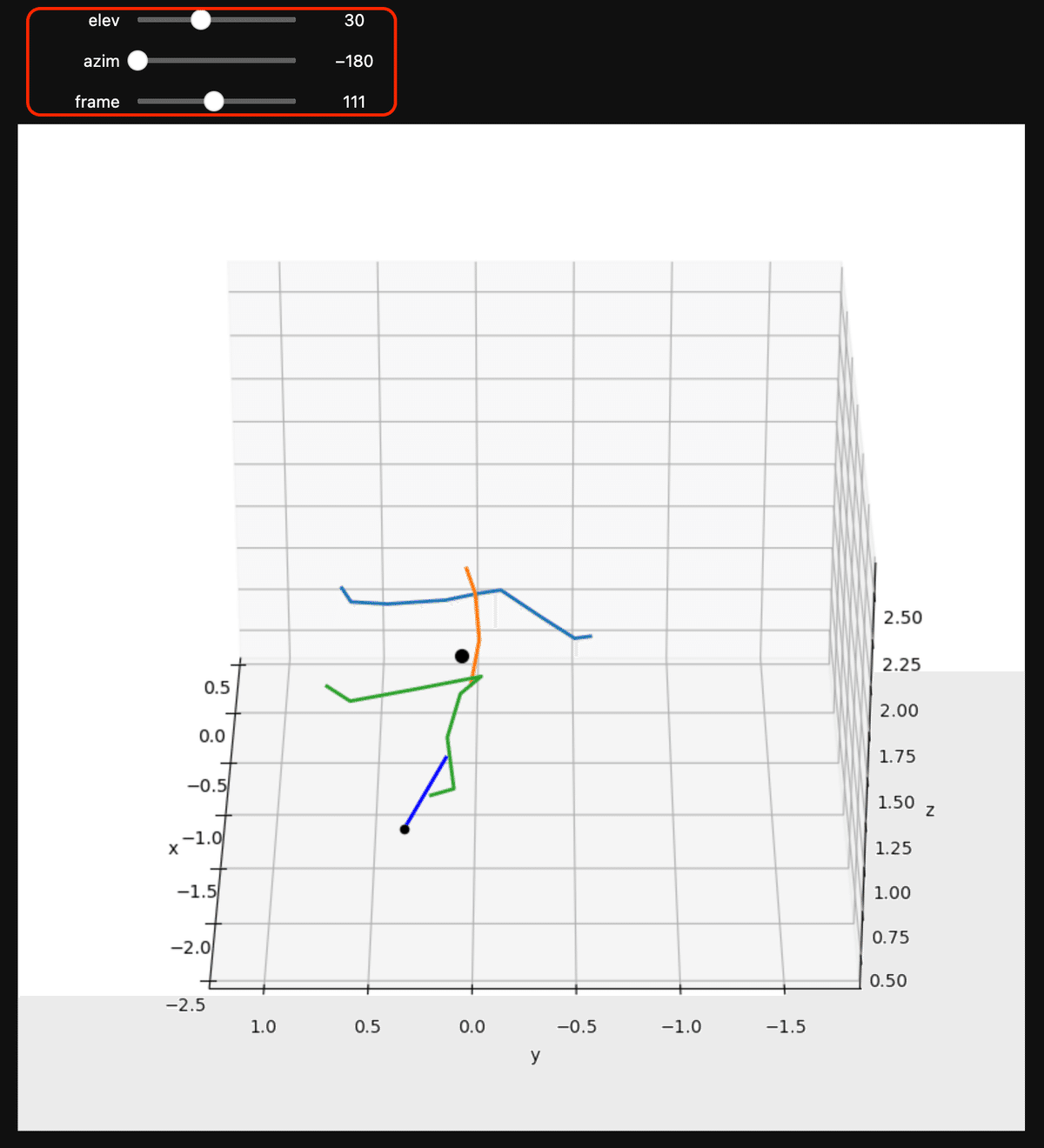
関数interact()を利用し,スライダーバーによってアニメーションを動かす方法で,ここでは視点も変えられるようにしている.確認には便利である.
def stick_c(ax, body_link, time, lw=1, xrange=(-1.5, 1.), yrange=(-1.0, 1.5), zrange=(0, 2.5)):
ax.plot(*bl.joint_p_list(body_link, time, bl.upper_arm_list), linewidth=lw, c='C0')
ax.plot(*bl.joint_p_list(body_link, time, bl.body_list), linewidth=lw, c='C1')
ax.plot(*bl.joint_p_list(body_link, time, bl.lower_body_list), linewidth=lw, c='C2')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_xlim(*xrange)
ax.set_ylim(*yrange)
ax.set_zlim(*zrange)
ax.set_aspect('equal') # Colab.では機能しない
def stick_c_plot_frame(body_link):
#upper_arm_list = [17, 6, 5, 4, 3, 7, 8, 9, 18] # 腕の関節位置
#body_list = [16, 3, 2, 1] # 頭から腰までの関節位置
#lower_body_list = [19, 12,11, 10, 13, 14, 15,20] # 下肢の関節位置
step_frame = 1 # アニメーションの際の描画でスキップするフレーム数
q = len(body_link[10].p) // step_frame # フレーム数をstep_sizeで割った,整数の商
max_frame = q * step_frame - 1 # 描画する最大フレーム数 len(body_link[10].p)#
@interact(frame = IntSlider(min=0, max=max_frame, step=step_frame, value=100, continuous_update=True), # 描画するframe
elev = IntSlider(min=-10, max=90, step=5, value=0, continuous_update=True), # ViewPoint(視点)の仰角
azim = IntSlider(min=-180, max=180, step=5, value=-180, continuous_update=True)) # ViewPointの方位角
def plot_3d(elev, azim, frame):
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection='3d')
ax.view_init(elev=elev, azim=azim)
stick_c(ax, b_link, frame, 2, (-2.5, .5), (-1.8, 1.2), (0, 3.))
plt.show()stick_c_plot_frame(b_link)2.FuncAnimation()による方法
# 3Dグラフ領域の作成
p_elev = 20
p_azim = -110
origin_o = [0,0,0] # 原点から見た力のモーメントを計算する
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection='3d')
ax.view_init(elev=p_elev, azim=p_azim)
xrange=(-2.5, .5)
yrange=(-1.8, 1.2)
zrange=(0, 3.)
f_max = 230 # 終わりのフレーム
step_frame = 5 # アニメーションの際の描画でスキップするフレーム数 (5より小さくするとメモリ不足で計算が止まるかもしれない)
f_para = .0005
cg = b_link[1].COG(bw, True) # 重心位置
zmp = bl.estimated_cop(bw, b_link, origin_o, weight=.00001, sf=360., grav=9.8)
force = b_link[15].ext_force
# アニメーション更新用関数の作成
def plot_3d(frame):
ax.cla()
stick_cg24(ax, b_link, cg, zmp, force, frame, time_lf_contact, time_lf_release, 2, f_para, xrange, yrange, zrange)
# アニメーションのオブジェクトを作成
anim = FuncAnimation(fig, plot_3d, frames = np.arange(0, f_max, step_frame), interval = 100)
# Jupyter内でアニメーションの表示
plt.close()
HTML(anim.to_jshtml())
### Gif/MP4に保存する場合 ###
#path_dir = '/Users/.../sample_data/' # 保存先のディレクトリの指定
#path = pathlib.Path(path_dir)
#path_gif = path.joinpath('animation_kick2.gif')
#anim.save(path_gif)
#plt.close()この方法は,1のようにインタラクティブに視点を動かすことはできないが,mp4やgifなどに出力できる.
下記アニメーションは,FuncAnimation()で作成している.コードはGoogle Colab.に示した.スティックピクチャの詳細は,これまでの章でも参照していただきたい.
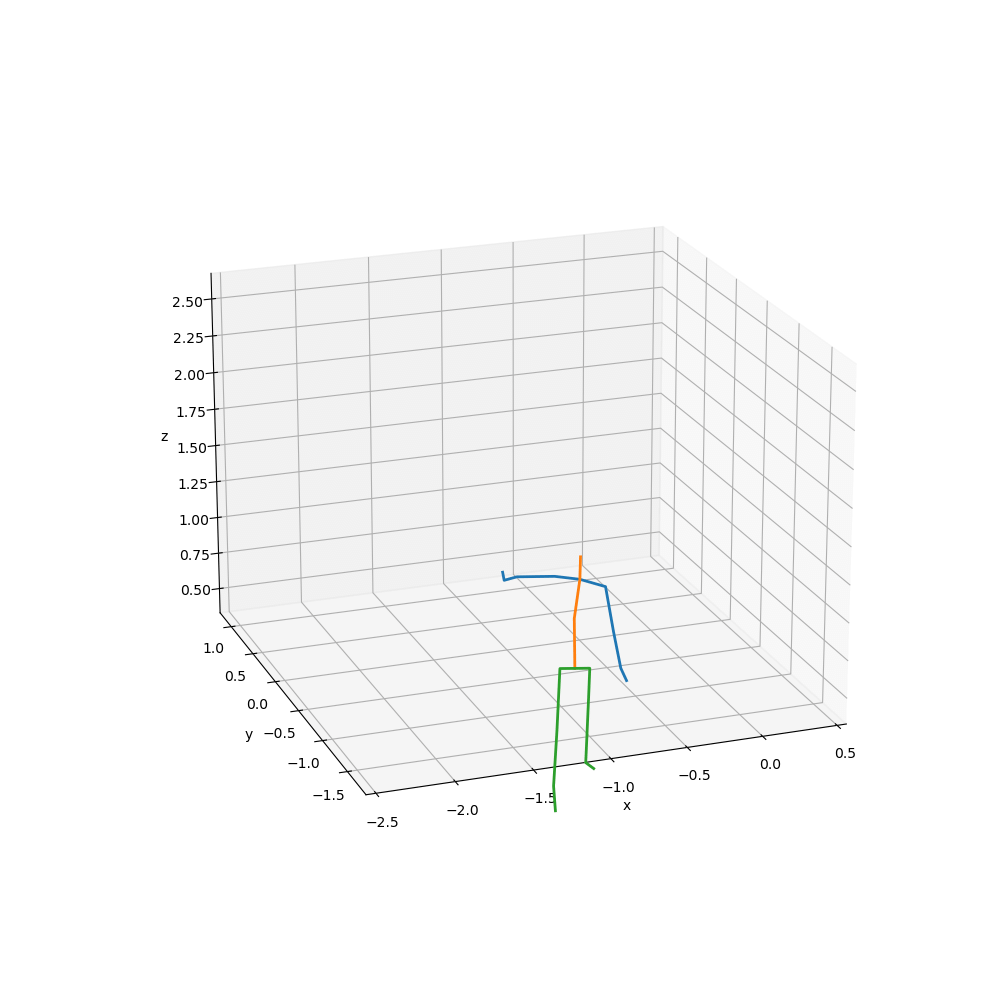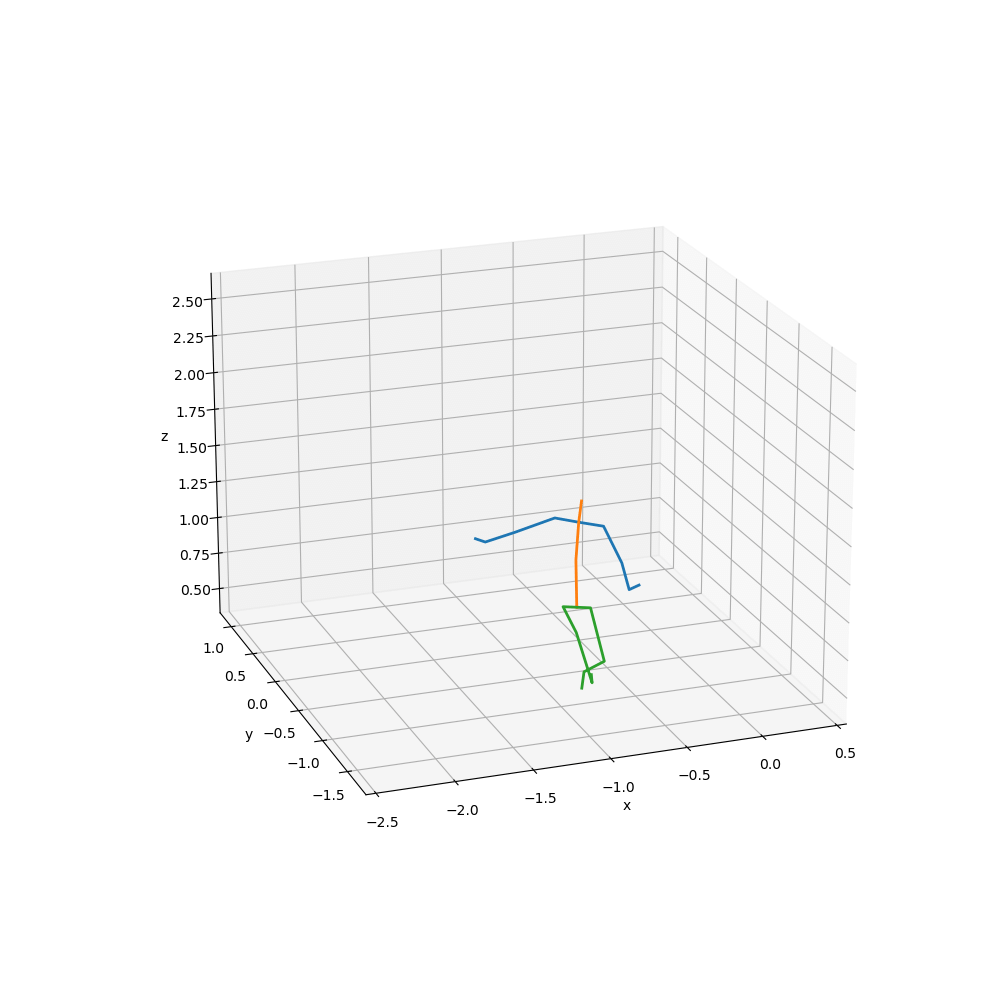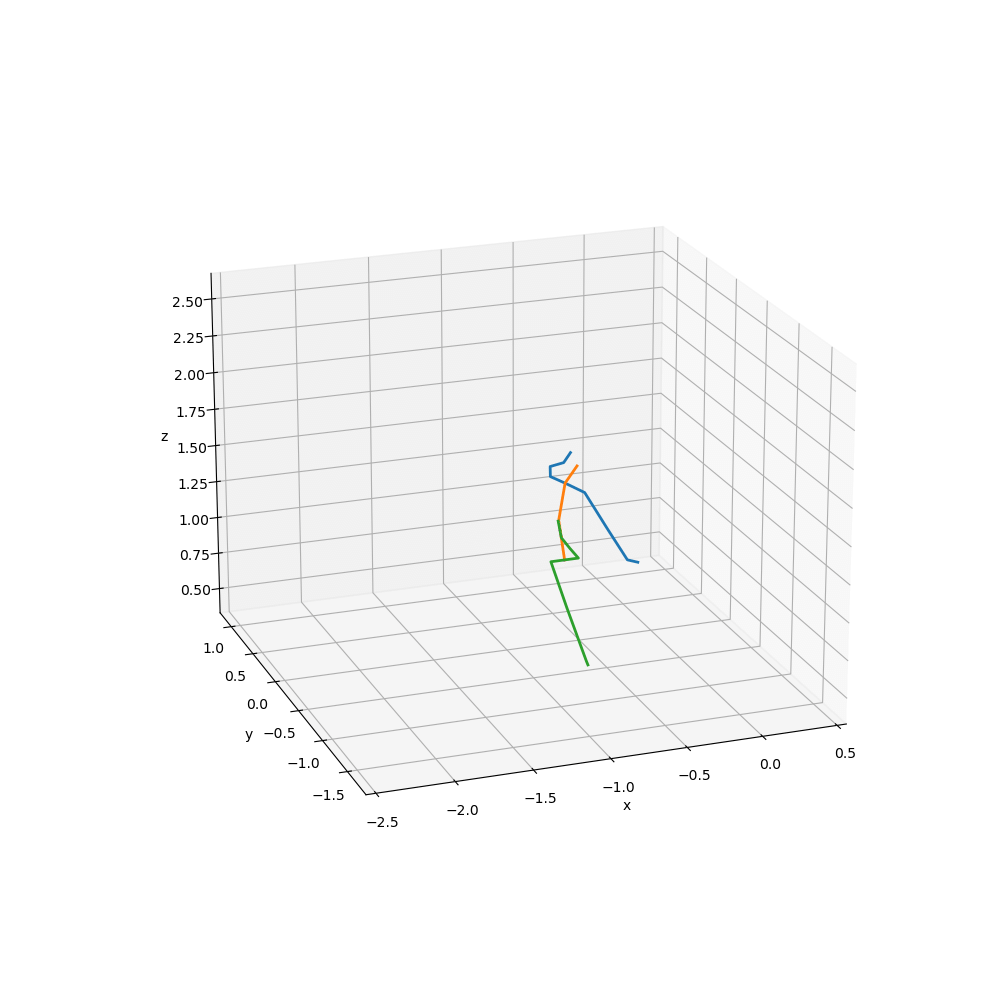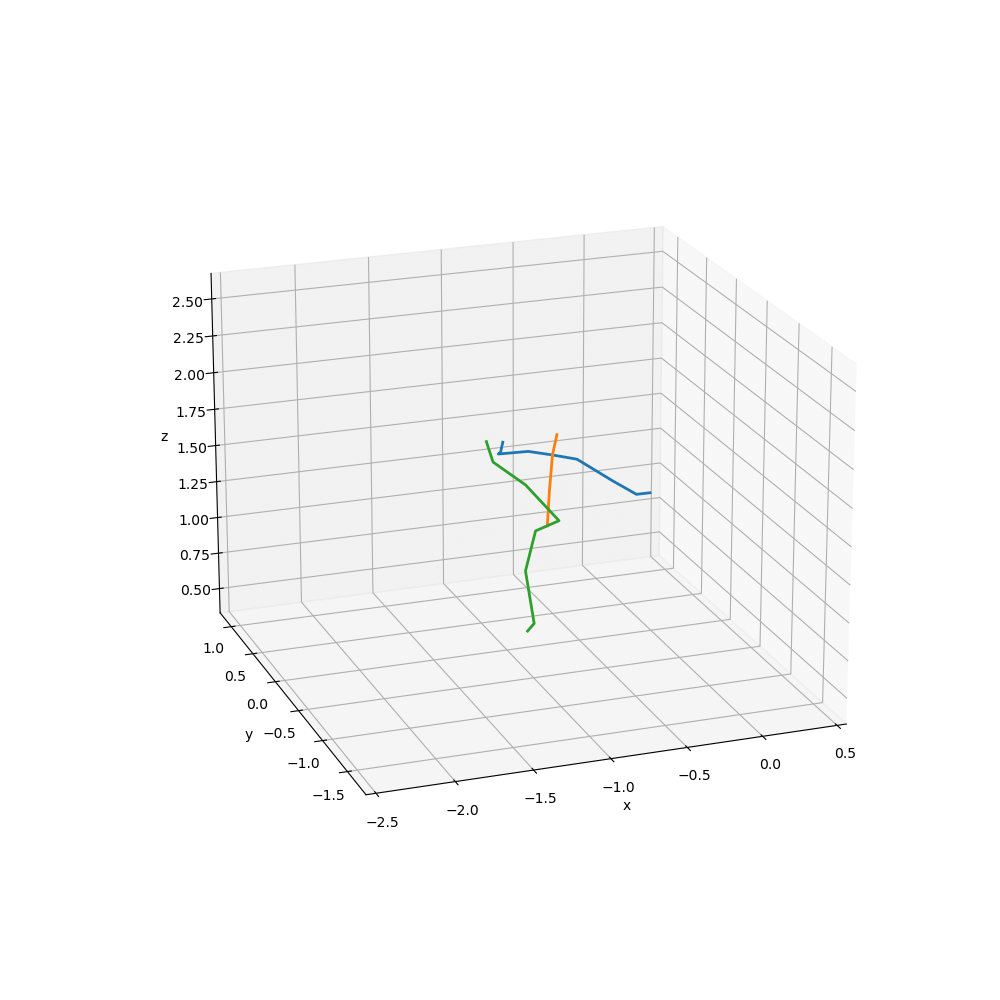
ここでは,スティックピクチャで確認し,
data_range = [70,300]でサンプルデータの70〜300のフレームだけを解析に使用することにした.なお,サンプリングレートは360Hzである.
2.フィルタリングのパラメータ
2-1.位置データの平滑化スプラインの重み係数
モーションキャプチャのデータには欠損値も誤差も含まれる.適切な力学計算を行う,ためにはマーカから位置,速度,加速度などを可能な限り正確に算出する必要があることはこれまでも述べた.また,特に力計算では加速度を必要とし,その加速度は位置を二階微分することによって取得できるが,微分演算はとにかくデータが暴れやすい.バターワースなどの周波数ベースのフィルタを使用すると,暴れないように遮断周波数を低めに設定すると,肝心の信号も低減させてしまう可能性が高い.
そこで,このシリーズでは平滑化スプラインを使用することで,少しでも正確な加速度を計算することに留意している.しかし,オリジナルの位置データがmm以下の精度が担保されなくては,いくらフィルタが優秀でも限界がある.したがって,力学計算でまずはモーションキャプチャなどで正確な計測を行うことがなによりも重要である.
平滑化スプラインについては
を参照されたい.
また,適切なフィルタの係数の選択は実際のデータの状態で変化し,適切な重み係数を選択する作業は不可欠となる(補足1).
ここでは,右大腿の原点(右股関節,l_id = 10)の位置をbl.joint_vec()関数で取得し,位置,速度,加速度の計算で平滑化スプラインの重み係数を変えながら,パラメーの選択を試行錯誤的に行う様子を示す.
下記のコードで,
# 生データ(右股関節)
plt.plot(bl.joint_vec(b_link, 10, file_path_op_24, version=3, unit=1.0))
plt.xlabel('Frame')
plt.ylabel('Position [m]')
plt.legend(['x', 'y', 'z'])右股関節(右大腿:l_id = 10 の原点)の座標をグラフに描くと,
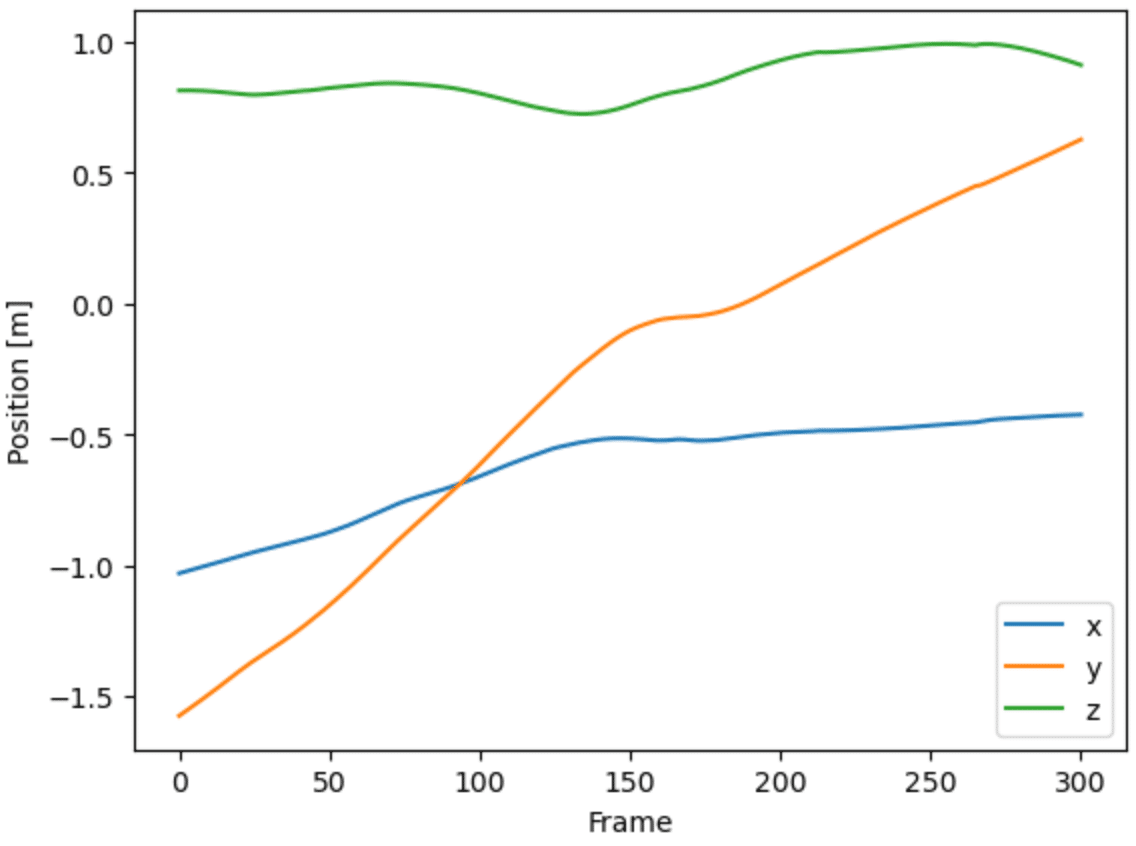
のようになる.ここでリンクの原点を取得する関数 joint_vec()(ファイルbody_link.pyで定義されているので,詳細はそちらを参照されたい)
joint_vec(b_link, l_id, file_path, version=2, unit=1.0, d_range=None)の各引数は,
b_link:クラスBody_Linkで定義されたクラス
l_id:同じくクラス Body_Linkのインスタンスで定義されている,部位のid.右大腿なら10を与える.
file_path:モーションキャプチャのcsvファイルのパス(例えば,Google Colabなら,'/content/drive/MyDrive/.../sample_sec_24.csv'のように与える)
version:これは,かなり計測環境に依存したオプションだが,OptiTrackの制御ソフトMotiveはバージョンなどによって出力形式を変更できるので,Motive3.0.Xで計測したデータは version = 3とし,過去の章で使用したデータはMotive 2.0.Xで計測しているのでversion = 2とする.今回はversion=3としていただきたい.
unit:位置データの単位がmではない場合など,単位を変更したい場合に使用する.今回のデータはmで計測し,そのままデフォルトの1を使用する.
d_range:もし,データを指定したフレームでトリミングする場合,トリミングの開始フレーム数f_sと,終端のフレーム数f_eをd_range= [f_s, f_e]で指定する.ここでは,1のトリミングで述べたように,data_range = [70,300] としている.
となっている.そこで以下で,このデータを時間微分し,平滑化スプラインの重み係数を決定する.ここで,
weight_p = .0001
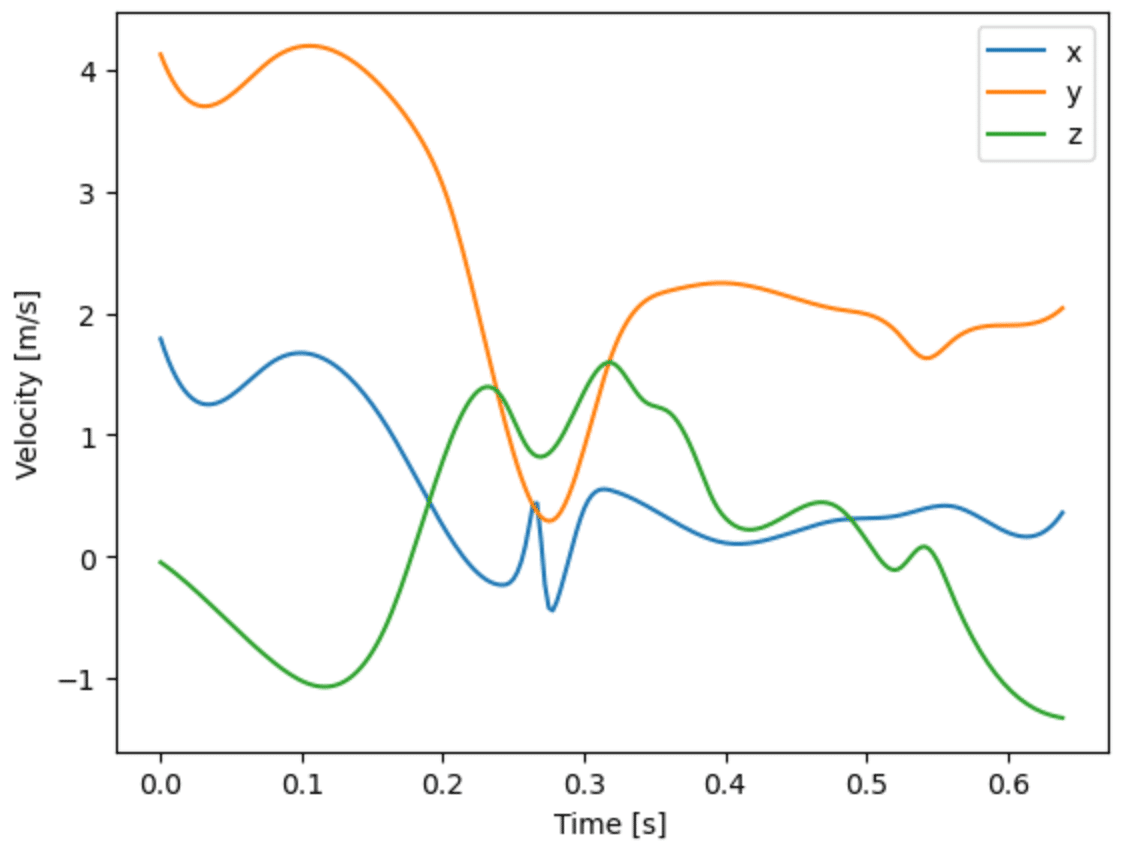
link_num = 10 # 右大腿の重み係数 weight_p と,部位のidであるlink_numを変え,全部位で下記のように「速度」のグラフ
# 速度
plt.plot(bl.smoothing_spline(
bl.joint_vec(b_link, link_num, file_path_op_24, version=3, unit=1.0, d_range=data_range),
weight_p, 360., order = 1)
)
や,
# 加速度
plt.plot(t_list,
bl.smoothing_spline(
bl.joint_vec(b_link, link_num, file_path_op_24, version=3, unit=1.0, d_range=data_range),
weight_p, 360., order = 2))
plt.xlabel('Time [s]')
plt.ylabel('Acceraation [m/s2]')
plt.legend(['x', 'y', 'z'])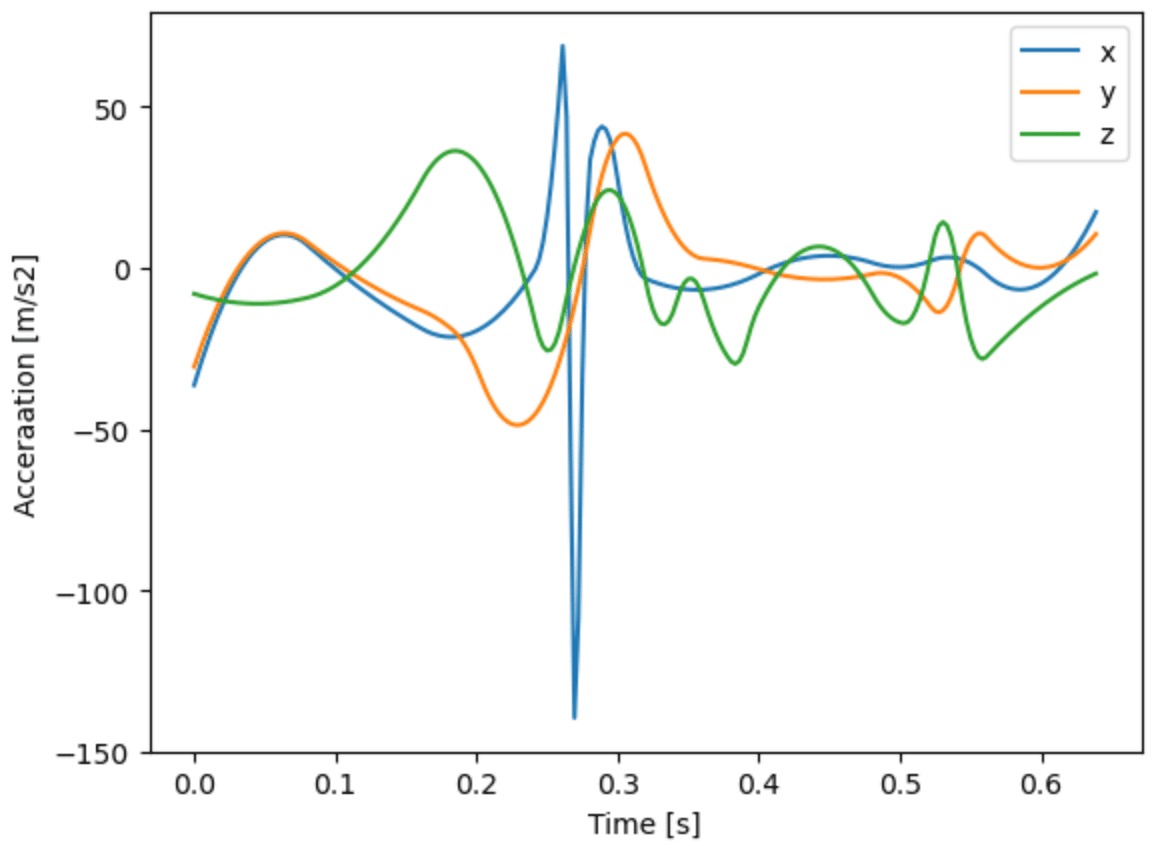
図3のような「加速度」のグラフを描くことで,確認していくことが求められる.欠損やノイズが混入していなければよいが,なにが起きているかは確認するまでわからない.
以上から,ここではこの作業を繰り返すことで,重み係数を
weight_p = .0001のように定め,以下でモーションキャプチャデータ(原点位置)pと,各部位の重心データcg,各部位の重心の速度vel,と加速度accを
# 手,前腕の姿勢回転行列を計算するためだけに必要なマーカの位置ベクトルもインスタンス変数pに格納
# 関節位置をBodyLinkのpに格納
bl.set_link_p_list(b_link, range(1,21), file_path_op_24, weight_p, 360., version=3, unit=1., d_range=data_range)
# ★230407変更・追加
# 姿勢回転行列を計算するために必要なマーカ位置ををBodyLinkのl_id: 21~34のpに格納
bl.set_rot_p_list(b_link, range(21,35), file_path_op_24, weight_p, 360., version=3, unit=1., d_range=data_range)
# 各linkの重心を,self.cgに格納
for n in range(1,16):
b_link[n].cg = bl.link_cg(b_link, n, file_path_op_24, weight_p, 360., version=3, unit=1., d_range=data_range)
# 各linkの重心の速度ベクトルをself.velに格納
bl.set_vel_link(b_link, range(1,16), .00005, 360.)
# 各linkの重心の加速度ベクトルをself.accに格納
bl.set_acc_link(b_link, range(1,16), .00005, 360.)変数b_linkに格納する.実際にご自身でこの行を行っていただき,ご自身でパラメータを選択していただければと思う.もちろん,部位によってこの係数を変えても良い.
なお,ここで筆者が選択している方法に関して述べると,重み係数の選択は,(物理的に事前知識が得られているわけでない場合,「それほど暴れるわけがない」,「それほど滑らかなわけがない」などの)主観以外のなにものでもない(補足2).本来はモーションセンサなどで同時に加速度計測を行うことで検証を行えばよかったが,今回はそのようなデータがないのでお許し頂きたい.
復習になるが,ここでClass Body_Linkで定義された変数b_linkは,クラスのインスタンス変数(b_linkに対する「属性」のような存在.第2章
を参照)として,p, cg, vel, accなどがファイルbody_link.pyに定義されているが,上記のコードで,全身の各部位の原点p,重心位置cg,重心の速度vel,重心の加速度accを格納し,たとえば
b_link[10].pには右大腿(l_id=10)の原点(右股関節)の位置ベクトルデータが格納されている.
2-2.回転データ(角度,角速度,角加速度)の平滑化スプラインの重み係数
回転データを計算する際にも時間微分の演算を含むため,ここで平滑化スプラインの重み係数を決定する必要がある.そこで,2-1と同様に,回転に関する姿勢角度(回転行列),角速度,角加速度のデータをb_linkに格納するために,ここで,平滑化スプラインの重み係数を決定する.
なお,ここで姿勢角度の計算方法を見直したので,そのことについて予め述べておく.
姿勢角度の計算方法の変更:
このキック動作の運動では,肘関節と膝関節の内外に補助マーカを貼付することで,上腕,大腿の姿勢角度計算方法を見直した.
第9章
で述べたこれまでの方法では上腕と前腕,または大腿と下腿の長軸に直交する軸を,肘関節軸,ないしは膝関節軸としたが(ファイルbody_link.pyに定義されているmethod1),ここで取り上げたキック動作では,肘・膝関節が伸展し2つの長軸がほぼ同じ方向を向いているため,精度と角度の符号の問題が発生する.そこで,肘,膝関節の蝶番関節の内外にマーカを貼付することで,method2に変更する.すなわち,
関節と関節を結ぶ長軸を$${z}$$軸とする.
関節の内外の補助マーカから蝶番関節の軸方向$${x'}$$を算出.
長軸$${z}$$と$${x'}$$に直交する$${y}$$軸を外積を用いて算出.
$${y}$$軸と長軸$${z}$$軸に垂直な方向として$${x}$$軸を算出.
の順番で軸方向を定める.
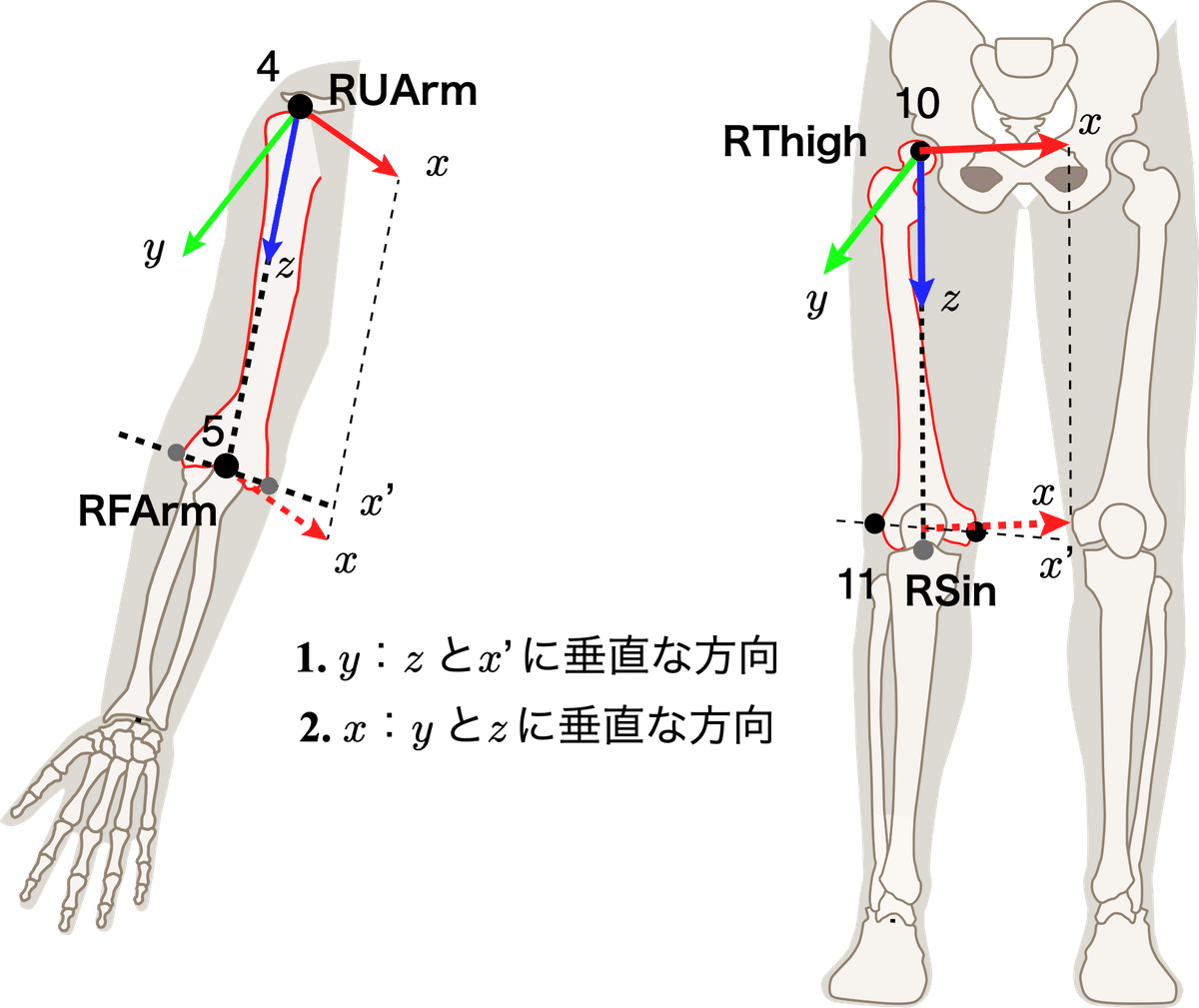
このように左右の上腕と大腿の座標系を定めるPythonコードで,method1からmethod2に変更を行い,
bl.set_frame_link(b_link, range(1,16), bl.frame_dict2)のように,各部位の姿勢角度をインスタンス変数rotに格納する.ここでbody_link.pyには,肘と膝関節の内外のマーカを利用する,新しい座標系定義bl.frame_dict2が加筆されている.
ここで,暫定的に,
weight_a = .005
link_num = 10 # 右大腿のようにに平滑化スプラインの重み係数weight_aを与え,下記のように,
plt.plot(t_list, bl.angular_vel_acc(b_link[link_num].rot, weight_a, 360.)[0])
plt.xlabel('Time [s]')
plt.ylabel('Angular velocity [rad/s]')
plt.legend(['x', 'y', 'z'])右大腿の角速度をグラフで描くと
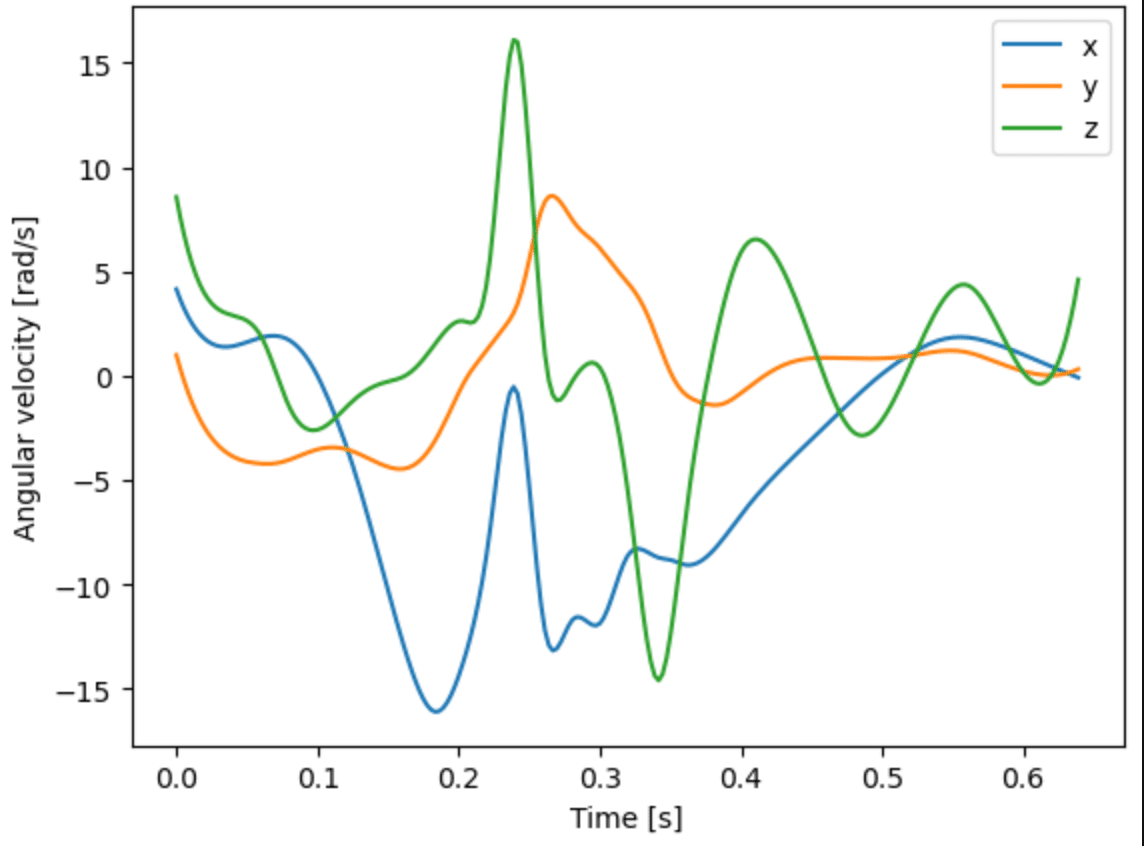
のようになり,同様に右大腿の角加速度を描くと,
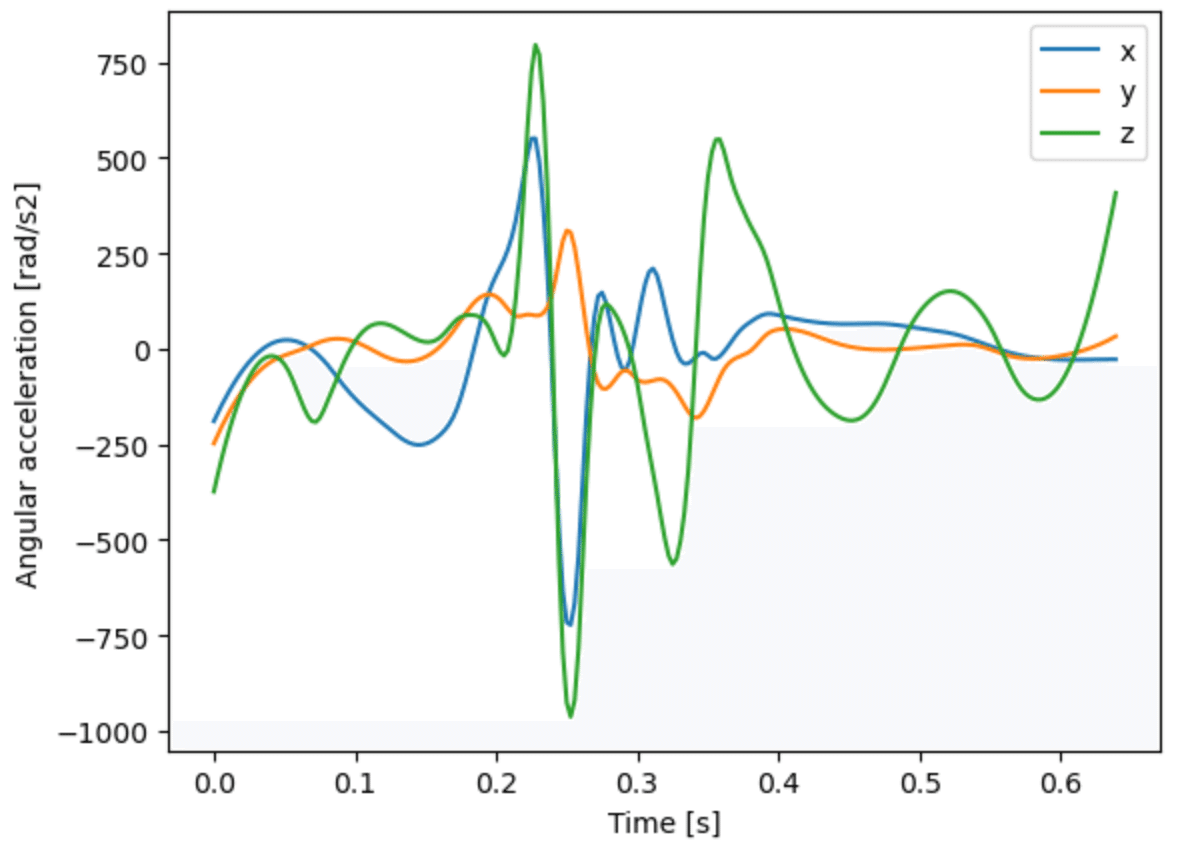
となるが,これを繰り返し,各部位の角速度と角加速度を決定し,角速度と角加速度を計算する際の平滑化スプラインの重み係数を
weight_a = .005とした.そこで,以下の関数で角速度と角加速度をインスタンス変数wとdot_wに格納する.
# 角速度と角加速度をw, dot_wに格納
bl.set_w_dotw_link(b_link, range(1,16), weight=weight_a, sf=360.)ここでは,すべての部位で同じパラメータで計算しているが,もちろん,部位によってこのパラメータを変えて,配列でパラメータを与えても良い.body_link.pyに記述したコードに修正を加えることはされほど難しくないはずだ.
このあと,以下のコードで,部位の長さを計算し,変数b_lengthに格納し,慣性モーメントを計算し,インスタンス変数inertia_momentに格納する.
# 各部位の長さの平均
b_length = [np.average(bl.link_length(b_link, i)) for i in range(1,16)]
# 体重86.0kgの被験者の慣性モーメントをb_linkのクラスに格納
bw = 86.
for l_id in range(1,16):
b_link[l_id].inertia_moment = bl.inertia_moment(bl.inertia_para_dict_m[l_id], bw, b_length[l_id-1])3.足部が接地しているフレームの確認
ここではフォースプレート(FP)を使用せず,外力として推定した床反力$${\bm{F}}$$と力のモーメント$${\bm{N}}$$を使用する.これらの計算は足部が地面と接地している時間以外もたとえば床反力であれば,
$$
\bm{F} = M (\ddot{\bm{x}}_G - \bm{g})
$$
から推定するが,接地している時間以外もこの値は計算される.そこで,下記のコードで床反力を計算すると,
plt.plot(t_list, bl.smoothing_spline(b_link[1].COG(bw, True), .00001, 360, order=2) - gravity)
plt.axvline(x = time_lf_contact/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_i/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_lf_release/sampling_rate, ls='--', c='.5')
plt.xlabel('Time [s]')
plt.ylabel('Force [N]')
plt.legend(['x', 'y', 'z'])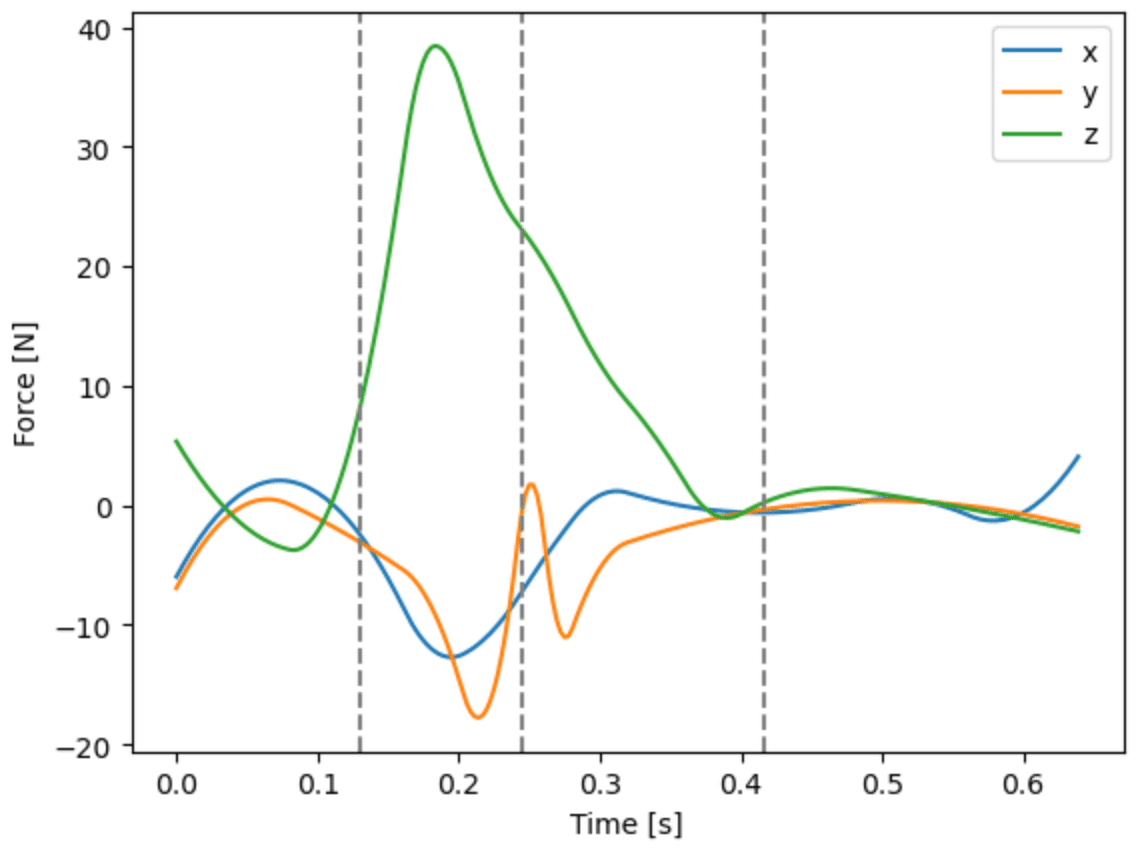
図7のようになるが,足部が接地していない時間も床反力が計算されてしまう.そこで,着地している足の判別と接地している時間(フレーム)情報が必要となる.ここでは,スティックピクチャと位置データなどから多角的に確認する.
さて,先程示したスティックピクチャや左足のデータから,ここでは左足接地している時間を,50~150フレームと判断した.詳細はGoogle Colabで参照していただきたい.そこで,
time_lf_contact = 50 # 接地開始
time_lf_release = 150 # 離地と定めた.また,ボールのマーカとボールを置いた座標(原点近く)から,ボールをキックした時間を
time_i = 88と定めた.
そこで,以下の関数bl.mask_array()
bl.mask_array(b_link, time_lf_contact, time_lf_release)で,0と1から構成される配列 [0, 0, .., 0, 0, 1, 1, 1, … 1, 1, 1, 0, 0, …, 0, 0] を作成し,これをマスクのように推定した力データに乗算することで,接地していない時間の力を0とし,以下のように,左右の足の遠位端のインスタンス変数ext_forceに,床反力を格納する.
# bw = 86.
# gravity = [0,0,-9.8]
b_link[12].ext_force = None #右足:使用するスライスしたデータには右足は接地していない
# 左足は
b_link[15].ext_force = bl.mask_array(b_link, time_lf_contact, time_lf_release) *\
bw * (bl.smoothing_spline(b_link[1].COG(bw, True), .00001, 360, order=2) - gravity)そこで,格納した左足に作用する力をグラフで示すと,
plt.plot(t_list, b_link[15].ext_force)
plt.axvline(x = time_lf_contact/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_i/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_lf_release/sampling_rate, ls='--', c='.5')
plt.xlabel('Time [s]')
plt.ylabel('Force [N]')
plt.legend(['x', 'y', 'z'])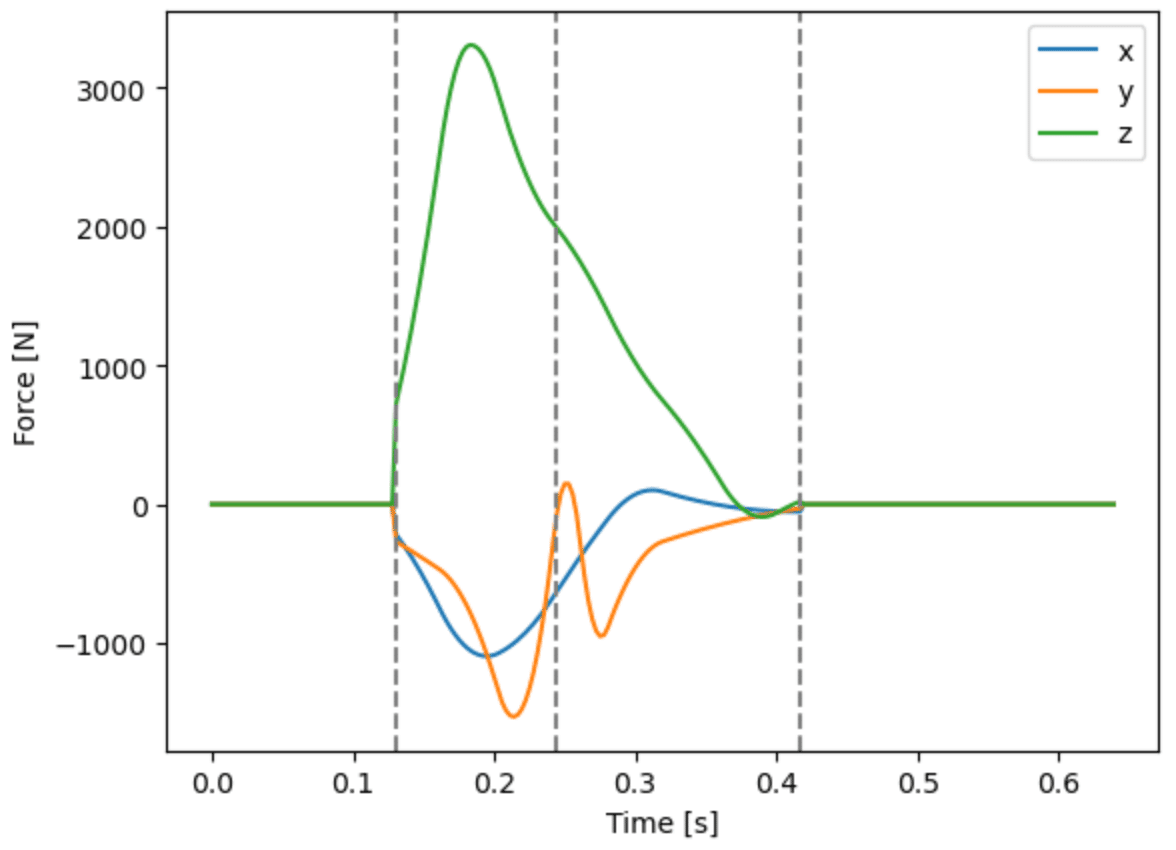
のようになる.
以下では同様に,外力として力のモーメントを計算するが,その前に,角運動量の時間微分について確認する.
4.全身の角運動量の計算方法の確認
詳細は前章(第23章)
を参照していただきたいが,左足の重心$${\bm{x}_{gb}}$$まわりの地面からの外力のモーメントは
$$
\bm{N}(\bm{x}_{gb}) =
\frac{d}{dt} \sum_{j=1}^n \bm{I}_j^j \bm{\omega}_j^j +
\sum_{j=1}^n \left(\bm{r}_{gj} \times m_j \ddot{\bm{x}}_{gj} \right)
- \bm{r}_G \times M\bm{g}
$$
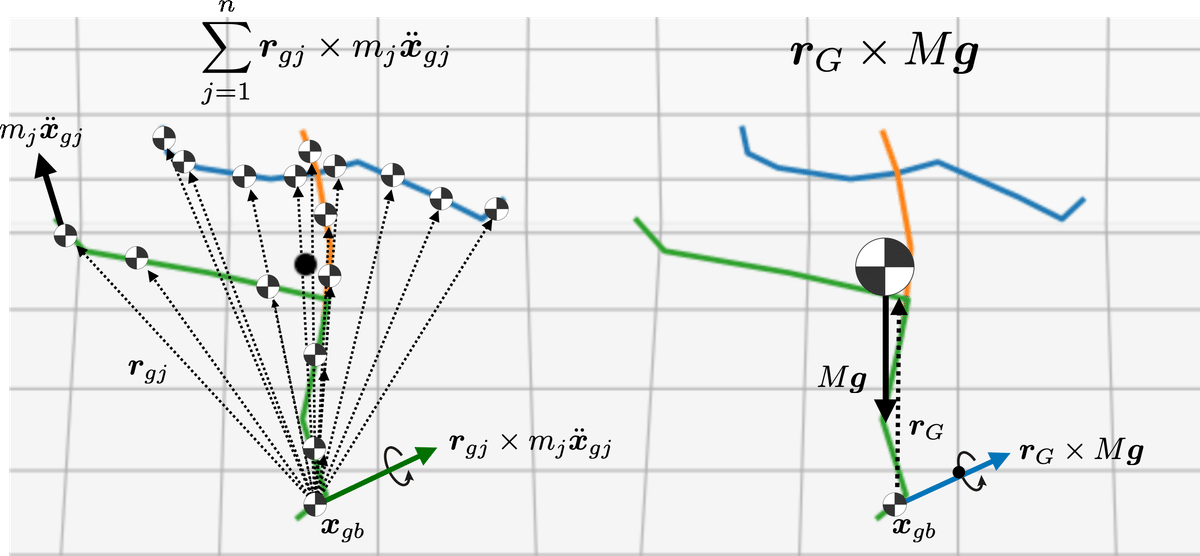
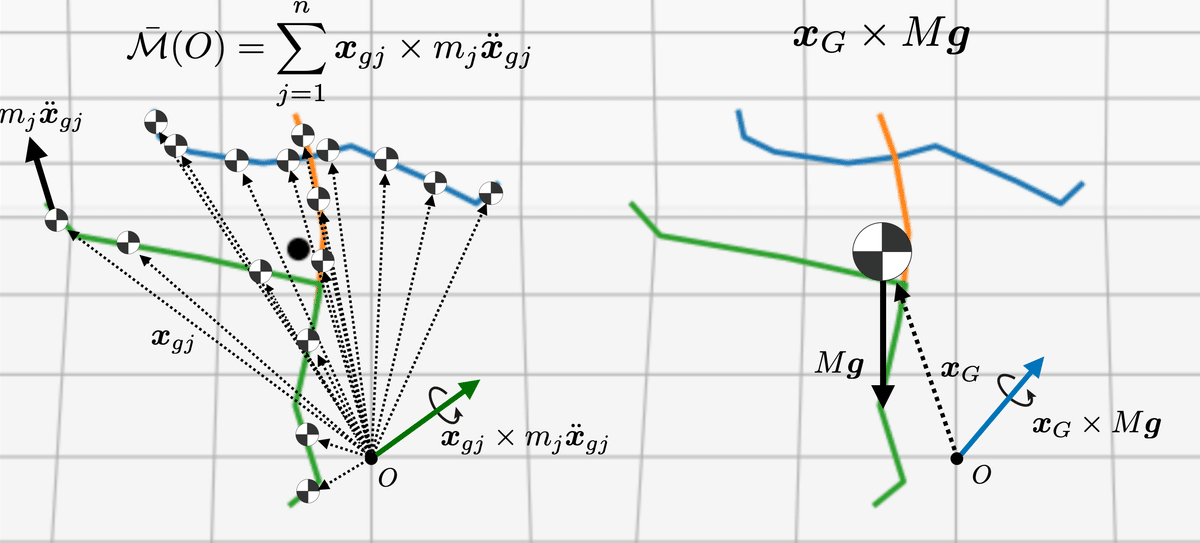
で計算され,右辺第1項($${\frac{d}{dt} \sum_{j=1}^n {}\bm{R}_j (\bm{I}_j^j \bm{\omega}_j^j) }$$)は全身の各部位の角運動量の時間微分である.この項は,着地している間,第2項,第3項($${\sum_{j=1}^n \left(\bm{r}_{gj} \times m_j \ddot{\bm{x}}_{gj} \right) - \bm{r}_G \times M\bm{g}}$$,図9)と比較して,運動によっては小さいことがあり,近似可能なことがあるため,このことを確認する.図9は回転のダイナミクスを計算する上でその意味が象徴されているので参照していただきたい.
図9左は第2項,すなわち左足足部の重心まわりの,各部位の重心の加速度$${\ddot{\bm{x}}_{gj}}$$に関するモーメントを,図9右は第3項,すなわち左足足部の重心まわりの,全身の重力$${M \bm{g}}$$に関するモーメントを示している.
なお,以下の計算では床反力同様に,関数bl.mask_array()でマスクを掛けている.また,角運動量の時間部分の計算で使用する平滑化スプラインの重みパラメータを
weight_am = .00001とした.これらの計算では,すでに角速度などは平滑化スプラインで計算されているため,重みパラメータ小さくてよい.
ここで上式の近似を用いず計算(全第1〜3項)を,近似を使用しない関数External_Moment()で行うと(前章のResultant_External_Moment()から関数名を変更),
# 1 (マスクもかける):近似なし
plt.plot(t_list,
bl.mask_array(b_link, 47, 150) * b_link[1].External_Moment(bw, b_link[15].cg, weight=.00001, sf=360., sister=True))
plt.ylim(-890, 390)
plt.axvline(x = time_lf_contact/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_i/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_lf_release/sampling_rate, ls='--', c='.5')
plt.xlabel('Time [s]')
plt.ylabel('Torque [Nm]')
plt.legend(['x', 'y', 'z'])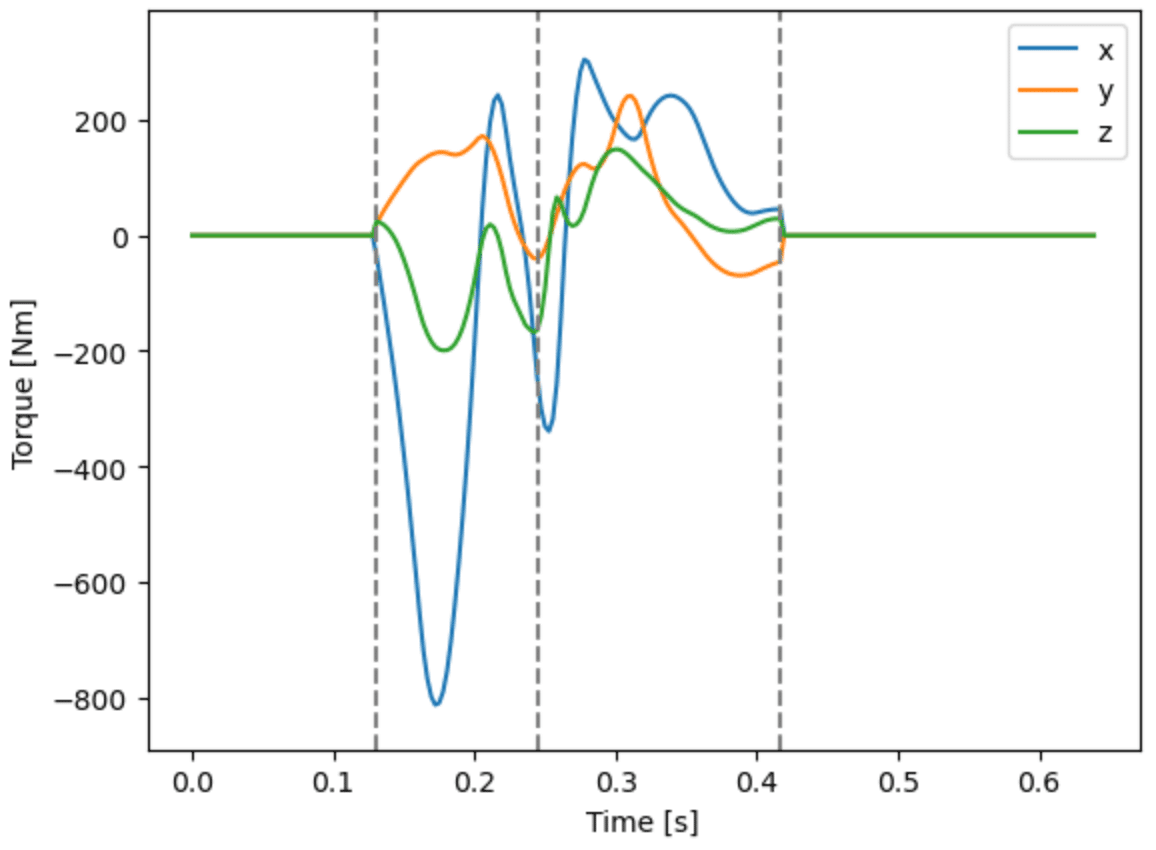
となり,次に第1項を省略する近似を行う,関数External_Moment_approx()で第2,3項だけを計算すると,
# 2 (マスクもかける):近似あり
plt.plot(t_list,
bl.mask_array(b_link, 47, 150) * b_link[1].External_Moment_approx(bw, b_link[15].cg, sf=360., sister=True))
plt.ylim(-890, 390)
plt.axvline(x = time_lf_contact/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_i/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_lf_release/sampling_rate, ls='--', c='.5')
plt.xlabel('Time [s]')
plt.ylabel('Torque [Nm]')
plt.legend(['x', 'y', 'z'])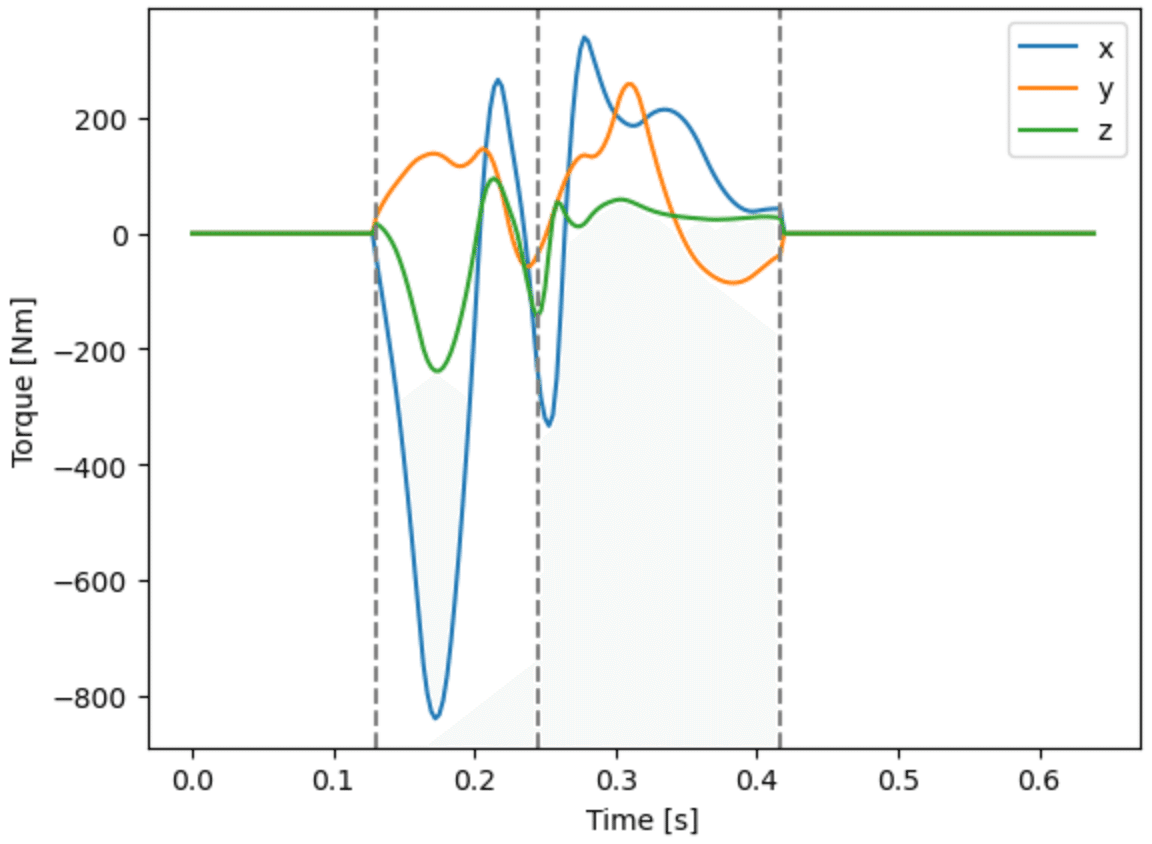
となり,一見すると違いが少なさそうだが,その差分である,第1項だけ計算すると,
plt.plot(t_list,
bl.mask_array(b_link, 47, 150) * \
bl.smoothing_spline(b_link[1].Net_Angular_Momentum(sister=True), weights=.00001, sf=360., order=1))
plt.ylim(-890, 390)
plt.axvline(x = time_lf_contact/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_i/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_lf_release/sampling_rate, ls='--', c='.5')
plt.xlabel('Time [s]')
plt.ylabel('Torque [Nm]')
plt.legend(['x', 'y', 'z'])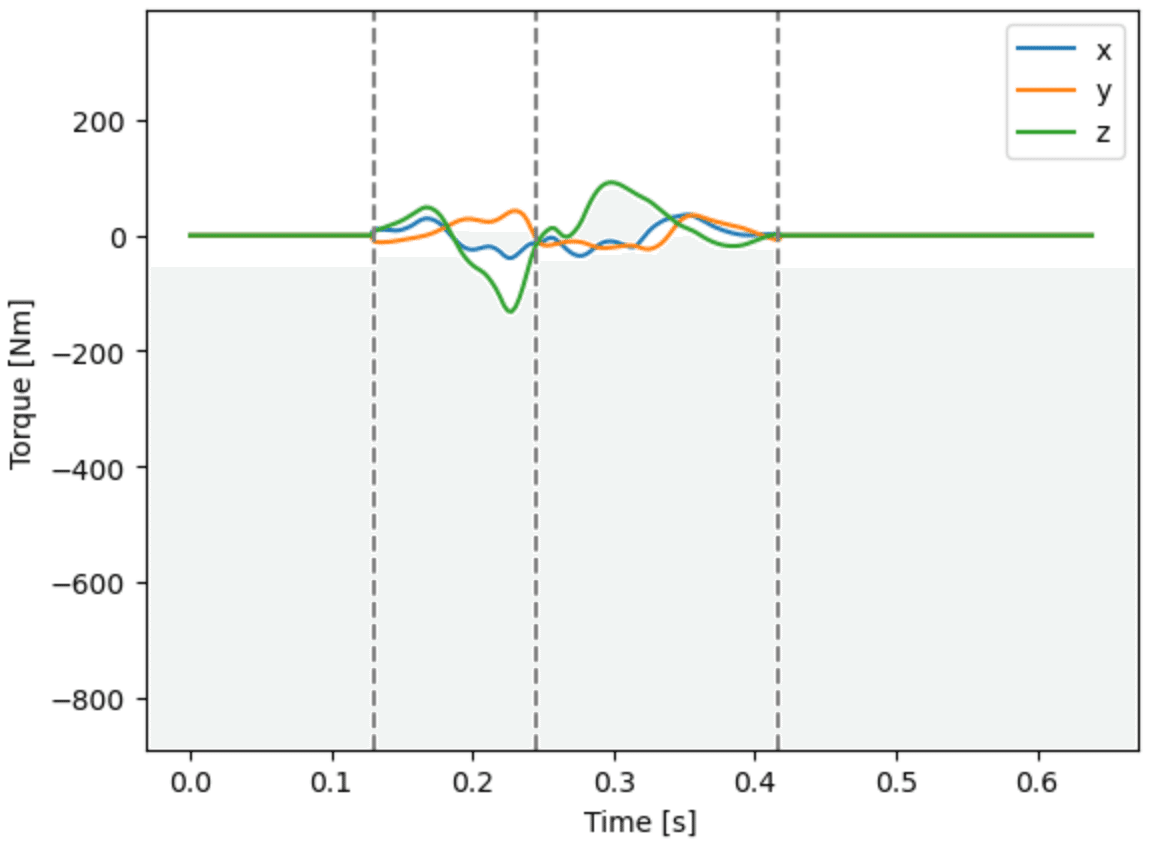
となる.他の項と比較すると小さいが,無視できるほどではないので,ここでは,近似せずに関数External_Moment()で外力のモーメントを計算する.
なお,スティックピクチャをみてもわかるが,右脚のキック動作はかなり高速に重たい下肢を振り回しているが,それでも図11に示された程度の角運動量の微分であることを考えると,身体がバランスさせる制御を行う上で,この値を小さくすることが重要であると言える.また,キックの前後でモーメントの帳尻を合わせている様子も伺える.
以上の結果から,左足の外力としての力のモーメント$${\bm{N}(\bm{x}_{15})}$$を
b_link[12].ext_moment = None
b_link[15].ext_moment = bl.mask_array(b_link, time_lf_contact, time_lf_release) * \
b_link[1].External_Moment(bw, b_link[15].cg, weight =weight_am, sf=360., sister=True)のように与えた.
plt.plot(t_list, b_link[15].ext_moment)
plt.ylim(-890, 390)
plt.axvline(x = time_lf_contact/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_i/sampling_rate, ls='--', c='.5')
plt.axvline(x = time_lf_release/sampling_rate, ls='--', c='.5')
plt.xlabel('Time [s]')
plt.ylabel('Torque [Nm]')
plt.legend(['x', 'y', 'z'])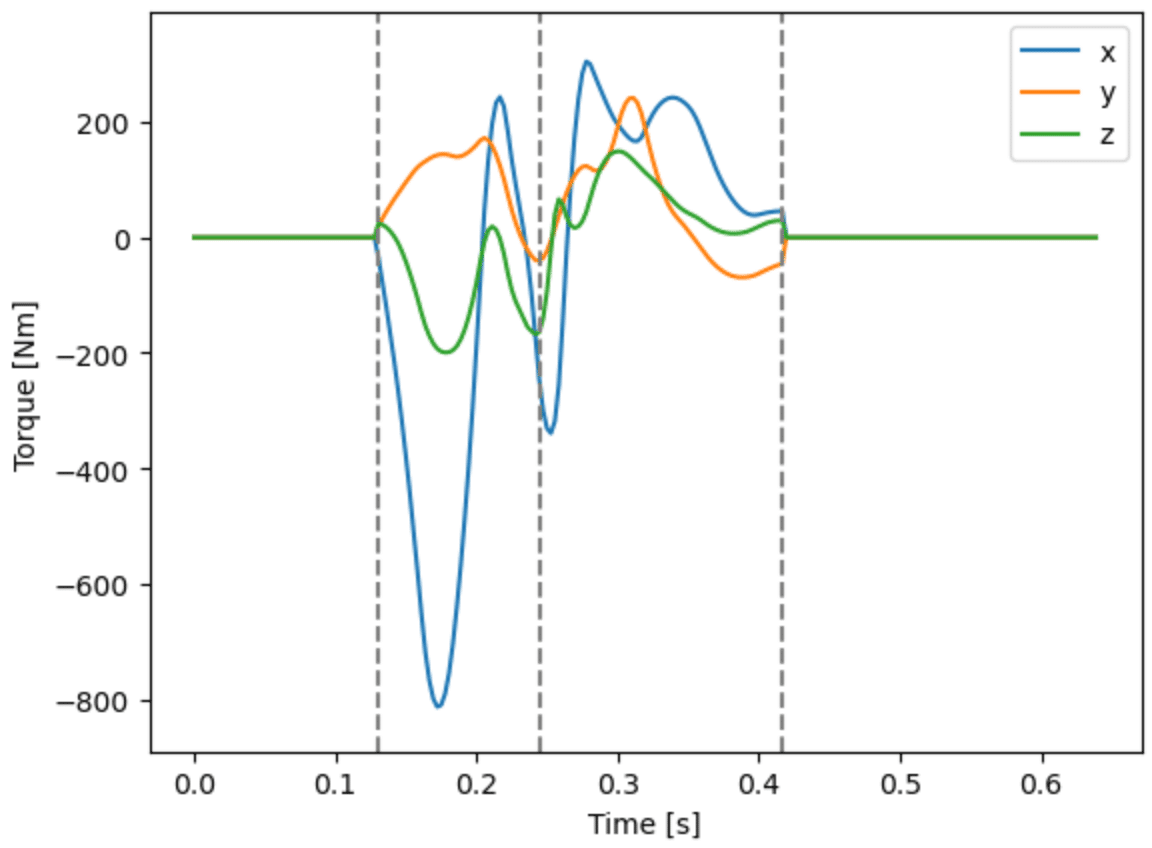
スティックピクチャ
関節に作用するトルクなどの解析は次回で行う.ここでは,COPを推定し,スティックピクチャを描くことを行う.
なお,ここで算出するCOPはロボティクスで定義されるZMP(zero moment point)に相当し,身体のダイナミクス(力学)から計算するCOPであるが,ここで計算するZMPは近似を使用していない点が,一般的なZMPとは異なるので注意されたい.
ZMPの推定
「フォースプレートによる床反力計測:第2章」
で述べてきたが,「地面から見た」原点$${O}$$まわりの身体と地面間に作用する力のモーメント$${\bm{N}(O)}$$を,COPに作用する力と摩擦のモーメントで記述し
$$
\bm{N}(O)=
\bm{c} \times \bm{F} + \bm{\tau}_z \\
=
\begin{bmatrix} 0 & -c_z & c_y \\ c_z & 0 & -c_x \\ -c_y & c_x & 0 \end{bmatrix}
\begin{bmatrix} M\ddot{x}_G \\ M\ddot{y}_G \\ M(\ddot{z}_G + g) \end{bmatrix}
+
\begin{bmatrix} 0 \\ 0 \\ \tau_z \end{bmatrix}
$$
ここで,$${\bm{c}= [c_x~c_y~c_z]^T}$$は原点$${O}$$から見たCOP(ZMP)の位置ベクトルであり,$${\bm{\tau}_z = [0~0~\tau_z]^T}$$は鉛直軸まわりの摩擦のモーメント,$${\bm{x}_G= [x_G~y_G~z_G]^T}$$は身体重心(質量中心)の位置ベクトル,$${M}$$は全身の質量(体重)である.また,$${\bm{F}}$$は床反力(地面反力)で,
$$
\bm{F}=M (\ddot{\bm{x}}_G - \bm{g}) = M \begin{bmatrix} \ddot{x}_G \\ \ddot{y}_G \\ \ddot{z}_G + g \end{bmatrix}
$$
である.
一方,第22章
第23章
などで述べてきたが,「身体側から見た」原点$${O}$$まわりの力のモーメントは,ヒトのダイナミクスから
$$
\bm{N}(O) =
\frac{d}{dt} \sum_{j=1}^n \bm{I}_j^j \bm{\omega}_j^j +
\sum_{j=1}^n \left(\bm{x}_{gj} \times m_j \ddot{\bm{x}}_{gj} \right)
- \bm{x}_G \times M\bm{g}
$$
となる.右辺の第2,3項の物理的意味を図14に示した.図9が左足重心($${\bm{x}_{15}}$$)まわりのモーメントであるのに対して,図14は原点$${O}$$まわりのモーメントである.違いに注意されたい.先程検証したように,キック動作では第1項の$${\frac{d}{dt} \sum_{j=1}^n \bm{I}_j^j \bm{\omega}_j^j }$$は無視できるほど小さくない.ここで,第1,2項を
$$
\bar{\mathcal{L}} \stackrel{\mathrm{def}}{=}
\sum_{j=1}^n \bm{I}_j^j \bm{\omega}_j^j
\\
=[\bar{\mathcal{L}}_x~\bar{\mathcal{L}}_y~\bar{\mathcal{L}}_z]^T
$$
$$
\bar{\mathcal{M}}(O) \stackrel{\mathrm{def}}{=}
\sum_{j=1}^n \left(\bm{x}_{gj} \times m_j \ddot{\bm{x}}_{gj} \right)
\\
=[\bar{\mathcal{M}}_x~\bar{\mathcal{M}}_y~\bar{\mathcal{M}}_z]^T
$$
と置くと,
$$
\bm{N}(O) =
\frac{d}{dt} \sum_{j=1}^n \bm{I}_j^j \bm{\omega}_j^j +
\sum_{j=1}^n \left(\bm{x}_{gj} \times m_j \ddot{\bm{x}}_{gj} \right)
- \bm{x}_G \times M\bm{g}
\\
=
\dot{\bar{\mathcal{L}}} + \bar{\mathcal{M}}(O) - \bm{x}_G \times M\bm{g} \\
=
\begin{bmatrix} \dot{\bar{\mathcal{L}}}_x \\ \dot{\bar{\mathcal{L}}}_y \\ \dot{\bar{\mathcal{L}}}_x
\end{bmatrix}
+
\begin{bmatrix} \bar{\mathcal{M}}_x \\ \bar{\mathcal{M}}_y \\ \bar{\mathcal{M}}_x
\end{bmatrix}
- M \begin{bmatrix} 0 & -z_G & y_G \\ z_G & 0 & -x_G \\ -y_G & x_G & 0 \end{bmatrix}
\begin{bmatrix} 0\\ 0\\ -g
\end{bmatrix}
$$
となるので,
$$
\begin{bmatrix} 0 & -c_z & c_y \\ c_z & 0 & -c_x \\ -c_y & c_x & 0 \end{bmatrix}
\begin{bmatrix} M\ddot{x}_G \\ M\ddot{y}_G \\ M(\ddot{z}_G + g) \end{bmatrix}
+
\begin{bmatrix} 0 \\ 0 \\ \tau_z \end{bmatrix}
\hspace{1cm}~
\\
~ \hspace{1cm} =
\begin{bmatrix} \dot{\bar{\mathcal{L}}}_x \\ \dot{\bar{\mathcal{L}}}_y \\ \dot{\bar{\mathcal{L}}}_x
\end{bmatrix}
+
\begin{bmatrix} \bar{\mathcal{M}}_x \\ \bar{\mathcal{M}}_y \\ \bar{\mathcal{M}}_x
\end{bmatrix}
- M \begin{bmatrix} 0 & -z_G & y_G \\ z_G & 0 & -x_G \\ -y_G & x_G & 0 \end{bmatrix}
\begin{bmatrix} 0\\ 0\\ -g
\end{bmatrix}
$$
を得る.ただし,ここで地面と原点の高さが同じとし,$${c_z = 0}$$とすると,COPの$${x, y}$$座標$${c_x, c_y}$$は
$$
c_x = \frac{-\dot{\bar{\mathcal{L}}}_y + \bar{\mathcal{M}}_y + Mg ~x_G }{M(\ddot{z}_G + g)}
\\
c_y = \frac{\dot{\bar{\mathcal{L}}}_x + \bar{\mathcal{M}}_x + Mg ~y_G }{M(\ddot{z}_G + g)}
$$
を得る.繰り返しになるが,アメフトのキック動作では,$${\dot{\bar{\mathcal{L}}} + \bar{\mathcal{M}}(O)}$$を無視できなかったので,ここでのZMPの計算ではこれを含めている点が,前章までに計算した$${\dot{\bar{\mathcal{L}}} + \bar{\mathcal{M}}(O)}$$を近似で無視して計算したZMPと異なるので注意されたい.
近似のないZMPのグラフを描くと,図14のようになる.
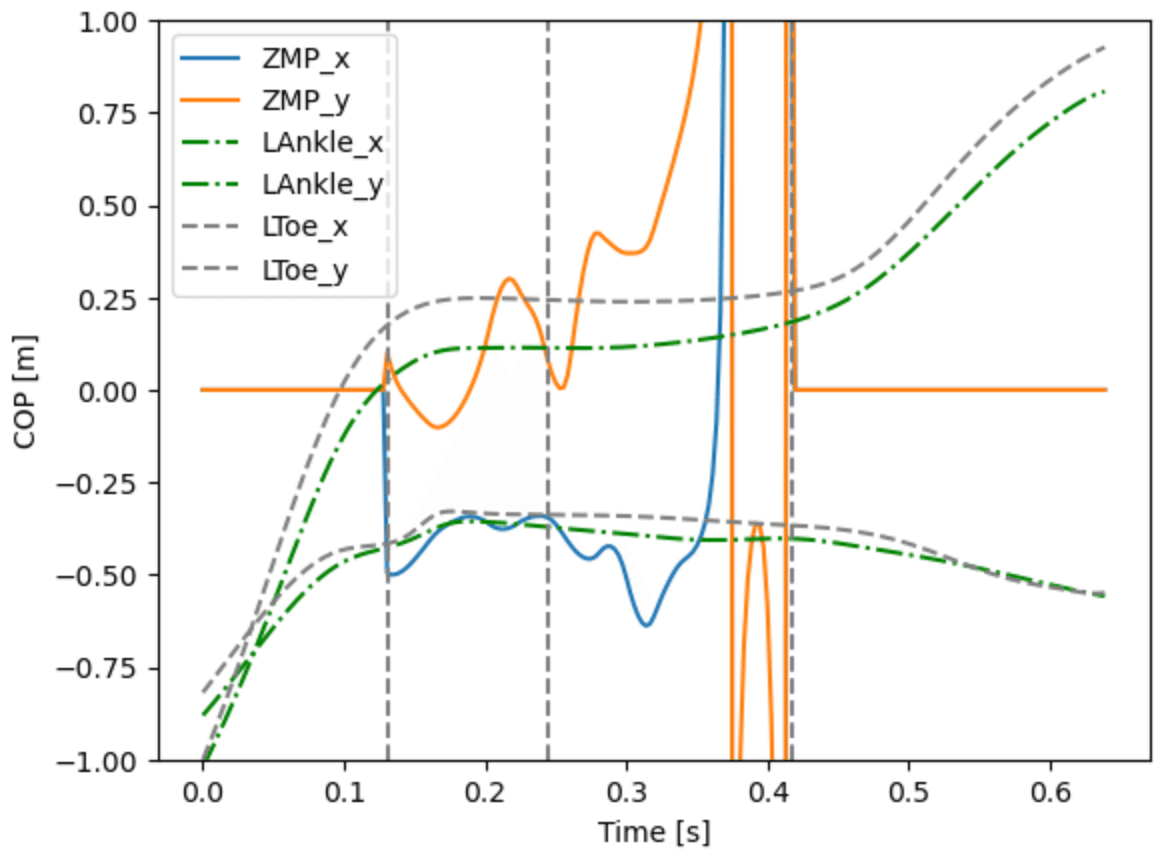
ZMPと左足の踵と爪先の座標を比較すると,キックの前半(接地からインパクト〜0.3 [s])ぐらいまでの推定精度は,それほどひどくないが,後半,床反力が小さくなるにつれて,急激に値が変化し精度が低下する.
これは,ZMPの計算で除算を含み,特に$${\ddot{z}_G + g}$$が小さくなるにつれて低下している.これは計算原理からいたしかたない.
このことをスティックピクチャを描いて確認する.ここでは,推定した重心位置,ZMP,床反力も示している.
def stick_cg24(ax, body_link, cg, cop, force, t, t_contact, t_release, lw=1, f_para =.001, xrange=(-1.5, 1.), yrange=(-1.0, 1.5), zrange=(0, 2.5)):
time = int(t)
ax.plot(*bl.joint_p_list(body_link, time, bl.upper_arm_list), linewidth=lw, c='C0')
ax.plot(*bl.joint_p_list(body_link, time, bl.body_list), linewidth=lw, c='C1')
ax.plot(*bl.joint_p_list(body_link, time, bl.lower_body_list), linewidth=lw, c='C2')
ax.scatter(*cg[time], s=50, c='k') # 重心
if t > t_contact and t < t_release:
ax.scatter(*cop[time], s=20, c='k') # 右足の重心
ax.plot([cop[time, 0], cop[time, 0] + f_para * force[time, 0]],
[cop[time, 1], cop[time, 1] + f_para * force[time, 1]],
[cop[time, 2], cop[time, 2] + f_para * force[time, 2]], c='b', linewidth=2) # 重心に作用する力(=床反力の合力)のベクトル
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_xlim(*xrange)
ax.set_ylim(*yrange)
ax.set_zlim(*zrange)
ax.set_aspect('equal') # Colab.では機能しない
plt.show()def stick_24_plot_time(body_link):
#upper_arm_list = [17, 6, 5, 4, 3, 7, 8, 9, 18] # 腕の関節位置
#body_list = [16, 3, 2, 1] # 頭から腰までの関節位置
#lower_body_list = [19, 12,11, 10, 13, 14, 15,20] # 下肢の関節位置
step_time = .02
sf = 360.
q = (len(body_link[10].p) / sf) // step_time # フレーム数をstep_sizeで割った,整数の商
max_time = q * step_time
f_para = .0005
cg = b_link[1].COG(bw, True) # 重心位置
zmp = bl.estimated_cop(bw, b_link, origin_o, weight=.00001, sf=360., grav=9.8)
force = b_link[15].ext_force
@interact(time = FloatSlider(min=0, max=max_time, step=step_time, value=0, continuous_update=True), # 描画する時間 [s]
elev = IntSlider(min=-10, max=90, step=5, value=30, continuous_update=True), # ViewPoint(視点)の仰角
azim = IntSlider(min=-180, max=180, step=5, value=-180, continuous_update=True)) # ViewPointの方位角
def plot_3d(elev, azim, time):
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection='3d')
ax.view_init(elev=elev, azim=azim)
time2 = time * sf
tl = time_lf_contact/sf
tr = time_lf_release/sf
stick_cg24(ax, b_link, cg, zmp, force, time2, tl, tr, 2, f_para, (-2.0, 1.0), (-1.5, 1.5), (0., 3.))スティックピクチャの結果は,Google Colabで確認をされたい.

次回について
今回,理論的な目新しさはなく,もし実際に解析を行う際の手順について示した.次回は,これを踏まえて,キック動作の力学解析の詳細を示す予定である.
補足
補足1:フィルタリングの課題
第5章
で,平滑化スプラインについて述べているが,このフィルタの最大の利点は加速度を計算する際のフィルタリングの精度で,筆者の知る限り,これ以上,加速度計算に適したフィルタは現在のところない.しかし,平滑化スプラインも万能ではなく,オンライン計算はできず,重み係数の選択の仕方もデータの長さ・単位(大きさ)・暴れ具合に依存し,それによって係数が大幅に変化する.平滑化スプラインの定義にも依存するが,ここで使用しているScipy.UnivariateSpline()の場合,0.00001ぐらいから100ぐらいを選択することもある.バターワースフィルタなどと比べると,フィルタのパラメータの選択にかなり注意が必要となる.位置データだけでなく速度や加速度の変化を眺めながら適切にパラメータ(重み係数)を選択する必要がある.
しかし,周波数ベースのフィルタリングでも,遮断周波数の選択を自動的に行う方法論は存在するが,実際にはそれほど機能しないことを考えると,フィルタリングのパラメータの試行錯誤的な選択の過程は必要不可欠で避けることができない.加速度がどのように変化するか事前知識・経験は必要だが,極論すると見た目の問題である.
そのことを考えると,平滑化スプラインのパラメータの選択は周波数ベースのフィルタと比較すると若干面倒だが,恩恵は十分に得られる.筆者はよほどデータの精度が高い,または非常に滑らかな運動ではない限り,現在のところこれ以外のフィルタで計算した加速度は正しくないだろうと考えている.
補足2:フィルタリングのパラメータの選択
正しい,フィルタリングのパラメータの適切な選択は難しい問題である.もし身長に選択をするなら,平滑化スプラインの定義と似ているが,別途正解となる加速度をモーションセンサなどで計測し,それとフィルタによって計算される加速度との近似度などから決定することができるだろう.身体全体でこのような検証は困難だが,ときどきこのような検証を行うことは必要だろう.ご自身で算出している加速度がどれだけ正確か,確認したことはあるでしょうか.



【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【サンプルデータについて】
ダウンロードしたサンプルデータは,研究室や所属団体内で自由にご利用いただいて結構です.ただし,学会発表,研究発表,論文などの体外的な活動でのご利用の場合は,株式会社スポーツセンシング社にご連絡ください.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
【データの計測について】
スポーツセンシング社のスタジオで,フォースプレートやモーションキャプチャを利用した計測も行えます.出力されるデータと,ここで示したプログラム(入力データの取り込み関数を少々改変する必要があるが)で,同様な解析を行えますので,まずはお気軽にお問い合わせください.
