
動かして学ぶバイオメカニクス#14 〜関節に作用するトルクの物理的意味〜
多体系の合成の「ニュートンの運動方程式」の物理的意味は明瞭である.もし床反力が身体に作用しているなら,床反力が操作できる唯一の外力となり,それは身体重心の加速度で定まり,全身の運動の仕方を拘束する.
一方,「オイラーの運動方程式」から関節に作用するトルクの意味を考えるためには,同様に合成の運動方程式を導く必要がある.しかし,これまで示した合成の回転の運動方程式には並進力が式に混在し,この式ではトルクの物理的意味がわからない.そこで,並進のダイナミクスと同様に,回転の合成の力学でも慣性力と重力加速度だけで記述できる形式に落とし込む.そして,そこから身体運動における回転のダイナミクスの重要な性質が見えてくる.これはトレーニングにおいても重要な考え方の根幹となるだろう.
はじめに
これまでの章
で,逆動力学計算における関節に作用する並進力と回転力を計算するコードを示した.これらの計算から定まる関節に作用する並進力や回転力(トルク)が,身体運動でどのような意味を持つのかを考えることが,このシリーズの目的のひとつであった.
そこで,その意味を見いだせるような形式に運動方程式を変えるのがこの章のひとつの課題となる.もし,トルクを計算する必要があるだけなら,本章はあまり役立たないかもしれないが,一度,ゆっくりと立ち止まってトルクの物理的意味を考えてみるとよいだろう.必ずしも関節を動かすのがトルクの役割ではない.
1.合成の運動方程式の計算ツールとしての意味
ここで示す合成の運動方程式は,関節に作用するトルクの計算ツールとしての視点では,トルクを「漸化的に計算しない方法」,または「並進力を介在させずに計算する方法」としてとらえることができる.漸化的な方法と比べれば多少効率は悪いが,上肢や下肢だけの合成の運動方程式をコードにする上では,人によってはコードが書きやすいかも知れない.
たとえば大腿,下腿,足の3リンクを考えた際の,合成の運動方程式から股関節に作用するトルク$${\bm{\tau}_1}$$は
$$
\bm{\tau}_1 = \bm{I}_1 \dot{\bm{\omega}}_1 + \bm{\omega}_1 \times (\bm{I}_1 \bm{\omega}_1) + \bm{I}_2 \dot{\bm{\omega}}_2 + \bm{\omega}_2 \times (\bm{I}_2 \bm{\omega}_2) + \bm{I}_3 \dot{\bm{\omega}}_3 + \bm{\omega}_3 \times (\bm{I}_3 \bm{\omega}_3) +\\
{}_{1}^{g1}\bm{p} \times(m_1 (\ddot{\bm{x}}_{g1} - \bm{g})) +
{}_{1}^{g2}\bm{p} \times m_2 (\ddot{\bm{x}}_{g2} - \bm{g}) +
{}_{1}^{g3}\bm{p} \times m_3 (\ddot{\bm{x}}_{g3} - \bm{g}) -\\
{}_{1}^{C}\bm{p} \times \bm{F} - \bm{\tau}_z
$$
と記述できる.詳細は以降の説明を読んでいただければと思うが,この式では関節に作用する力$${\bm{f}_1, \bm{f}_2, \bm{f}_3}$$が消え,漸化形式でもない.力のモーメントも「全て股関節まわりのモーメント」として記述され見通しが良い.
2:合成の運動方程式の身体運動の制御論的意味
式の導出を読み飛ばしたい読者のために,「身体制御の視点」から,もう一つの回転の合成の運動方程式の重要な意味を予め述べておこう.

トルクを計算するだけなら,下肢はただの棒と考えれて良い.
たとえば,図1(左)に示した投球時の前足(踏み込み足)のように,地面と接触している側の下肢には大きな外力(床反力)が作用し,接地側の下肢全体に大きな並進の力とトルクが作用する状況を想像していただきたい.もう少し具体的に述べると,股関節には大きなトルク$${\bm{\tau}_1}$$と,足(COP)に大きな地面反力$${\bm{F}}$$と摩擦のモーメント$${\bm{\tau}_z}$$が作用している.また,股関節から足(COP)までを一つの梃子(てこ)とみなし,その位置ベクトルを$${\bm{r}}$$とする.このような状況下では,回転の慣性力項$${\bm{I}\dot{\bm{\omega}} + \bm{\omega} \times (\bm{I} \bm{\omega})}$$や,並進の慣性力$${m \ddot{\bm{x}}_g}$$や重力$${m \bm{g}}$$に関する力のモーメントは,この外力と比較すると無視できるほど小さく,それらの外力が作用する近くの部位の関節に作用するトルクは
$$
\bm{\tau}_1 \approx -\bm{r} \times \bm{F} - \bm{\tau}_z
$$
のように,静力学的なつりあい式で記述できる.つまり,もはやこれは運動方程式ではなく摩擦のモーメントの他,先程示した右辺の最後の2つの項を残しただけの式となり,長かった式も条件を満たせば,これだけの式に簡略化できる.つまり,多少動いてはいるが,力学的にはむしろ棒を床と壁に立て掛けた状態に近いといえ,正確に述べると壁はなく,図1右のような壁の代わりのトルクと反力の力の釣り合いとなっている.もはや,膝や足首の関節の有無と関係なく,股関節のトルクを計算する上では,股関節から地面まで一つの棒と考えてよい.膝関節の力が弱ければ,床反力(地面反力)が小さくなるだけのことだ.後述するが,トルクを大きくするような下肢の姿勢も議論が可能となる.
これは簡便で便利な性質である.面倒な加速度などの計算が不要で,フォースプレートで床反力と摩擦モーメント,さらに股関節の位置を計測すれば股関節まわりのトルクが推定できる.ここでは,これを「静力学的近似」と呼ぶことにする.ただし,末端に外力が作用せず,高速に運動するようなスイング運動などでは成り立たないことには注意されたい.あくまでも大きな外力が作用する部位近傍(上肢,下肢などの四肢単位と考えればよいだろう)で成立する性質である.
なお,どの程度この近似が成立するかは運動に依存するが,これまで取り上げたバランス動作のデータを使用し,関節に作用するトルクを通常の力学計算を行った場合と,慣性力を無視して計算したトルクをこの章の後半で比較する.
このような近似は,歩行やランニングの支持脚,ゴルフスイングや,サッカーのキック動作(支持脚)などでも確認をしており,恐らく殆どの運動で慣性力を無視してもよいだろう.筆者は直接確認していないが自転車の下肢も恐らく同様であると聞いている.柔道で手先に大きな外力が作用している上肢などにも当てはまることが十分予想される.支持脚をストッパーのように支えるキック動作ならまだしも,歩行やランニングのように移動する下肢でも慣性力が小さいという事実は,筆者にとってはなかなかの驚きであった.
これまでの経験では,工学系の研究者でもこの事実は意外と想像していない人が多いようで,驚く人も多く疑う人もすらいるが,読者も最後の計算やご自身のデータで確かめていただければと思う.
また,関節に作用するトルクが上記の式で定まるなら,トルクは「床反力ベクトルの方向」と「姿勢」で決まることを意味する.外積の幾何学的意味が理解できれば,このことは容易に理解できるはずである.外積については
を参照されたい.
なお,このことは身体運動の制御において,もうひとつの重要な意味がある.
たとえば全身運動では床反力のような外力を有効利用するために,ヒトは回転の運動方程式における慣性力を小さく,すなわち「身体を回さないように(動かないように)制御している」ことの表れで,言い換えるならば,「並進の外力を伝達するために運動を制御している」ことを意味する.つまり,トルクは関節を動かすために作用させているのではなく,力の伝達のためにむしろ関節を動かさないように投句を発揮していることを示している.これはスポーツに限った話ではなく,歩行のような日常の身体運動でも同様である.
さらに述べるなら,エリートアスリートほどこの傾向は強い.ぐらついているようでは,大きな力を伝達できないためと考えられる.また,たとえスイング運動のような高速に運動している上肢でも,末端に外力も作用せず近似は成り立たないが,伝達すべき物理量は回転力ではなく,並進力である事自体は同じである.
このあと,まず冒頭の式の導出を行う.ただし2リンクモデルでの簡単な計算なので,この近似を利用する方はご自身で導出を確認をしていただきたい.
関節に作用するトルク
これまでの議論で述べてきたように,部位$${i}$$の運動方程式
$$
\bm{I}_i \dot{\bm{\omega}}_i + \bm{\omega}_i \times (\bm{I}_i \bm{\omega}_i) = {}_{gi}^{i}\bm{p} \times \bm{f}_{i} - {}_{gi}^{i+1}\bm{p} \times \bm{f}_{i+1} + \bm{\tau}_i - \bm{\tau}_{i+1}
$$
における$${\bm{\tau}_i , \bm{\tau}_{i+1}}$$は,関節に作用するトルクで,これは筋張力の発揮が関節レベルでトルクに還元されたものである.バイオメカニクスではこれを関節トルクと呼ぶ.ロボットでもアクチュエータが関節に作用し駆動力を制御するので,これを関節駆動力と呼ぶこともある(補足1).
合成の運動方程式
復習:合成の並進の運動方程式
前章では,全身の合成のニュートンの運動方程式
$$
\sum_{i=1}^n m_i (\ddot{\bm{x}}_{gi} - \bm{g}) = M (\ddot{\bm{X}}_{g} - \bm{g}) = \bm{F}
$$
の外力が床反力$${\bm{F}}$$になることを示した.ここで,$${m_i}$$は身体各部位の質量,$${\bm{x}_{gi}}$$は部位の重心の位置ベクトル,$${\bm{g}}$$は重力加速度ベクトル,$${M}$$は身体の質量,$${\bm{X}_{g}}$$は身体重心の位置ベクトルである.これは一体何を意味するのだろう.
このことは,まずフォースプレートを持ち合わせなくても,正確な計測と適切なモデリングと適切なフィルタリングによって,「床反力を意外と高精度に推定できる」ことを示している.どの程度,推定が成り立っているかは,
の図3をご覧になっていただきたい.もちろんこれはタスクに依存するが計算において注意を払えば,このように高精度に推定ができることがわかるだろう.ただし,左右の足への床反力の分配は単純にはできない.いまのところ機械学習では可能かもしれないが,理論的には一般化はいまのところ厳しい(ただし,投球時の床反力ぐらいなら,物理的に妥当かどうか別として,仮定を設ければ左右への分配はそれほど難しくないかもしれない).
いずれにせよ,この性質は便利だ.
しかし,それ以上に重要なことは,このことは全身の系(システム)の外力が床反力である場合,それは身体重心の加速度と重力加速度で決まることを示している.なお,系とはとりあえず対象範囲と考えておけば良い.いまフォースプレートは全身の系外の外部環境と恣意的に考えているだけで,その境界は都合よく勝手に定めて良い.
このことは,たとえば速く走るための力学問題は,身体重心の加速度を大きくする問題を考えることになる.より詳細に述べると,床反力を最大化しつつ,その力を重心方向に作用させるように同時に制御を行っていると言える(文献1).
なお,当たり前だが,走速度は進行方向の水平の床反力で定まる.鉛直方向の床反力の大きさに注意がいきがちだが,ロコモーション(移動)では,最終的には水平方向の床反力が重要である.この水平の床反力が大きくなるように,身体重心の加速度を制御することが走速度を高める際の力学的な課題となる.
これは,移動運動における「物理的な必然性」で解釈の余地はない.
合成の回転の運動方程式
一方,合成の回転の運動方程式では,同様に床と身体間に作用する力のモーメントが,唯一の回転としての外力となり.走る例を考えるならば,これが転ぶか転ばないかを定める.ヒューマノイドのロボティクスの研究者にとっては,この転倒条件のほうがどちらかというと重要であるかもしれない.
しかし,前述のようにバイオメカニクスにおける関心は並進力のほうに関心が高いだろう.たとえば走運動では,水平の床反力を最大化することが目的であり優先される課題であるが,それを実現するために回転のダイナミクスが補助的に関係するという構図になる.つまり,全身の関節に作用するトルクによって床反力をどのように最大化するかを考えていく必要がある.
以下で,合成の回転の運動方程式を導出する.以下の導出は読み飛ばしてもかまわないが,図3を見ながら運動方程式の構造は確認したほうが良い.
合成の回転の運動方程式の導出
第11章
で,合成のオイラーの運動方程式
$$
\bm{\tau}_i = \sum_{i}^n \left(\bm{I}_i \dot{\bm{\omega}}_i + \bm{\omega}_i \times (\bm{I}_i \bm{\omega}_i) \right) + \sum_{i}^n \left(-{}_{gi}^{i}\bm{p} \times \bm{f}_{i} + {}_{gi}^{i+1}\bm{p} \times \bm{f}_{i+1} \right)
$$
を導いた.トルクを数値的に計算するだけならこの式のほうが良いのだが,この式には慣性力以外に,各部位と部位の間の関節$${i}$$に作用する力$${\bm{f}_{i}}$$が混在し,これではトルクの物理的意味が見えてこない.

そこで,まず力$${\bm{f}_{i}}$$をこの式から消去することを試みる.また,話を簡単にするために,ここでは簡単のために図2のような2リンク(2つの部位から構成される)機構を考える.足部がなく大腿(部位1)と下腿(部位2)から構成される下肢を想像していただくと良い.また,下肢は地面と接触し,部位2には,摩擦のモーメント$${\bm{\tau}_z}$$と,COPの位置$${\bm{x}_C}$$に床反力$${\bm{F}}$$が作用する場合と考える.
すると前述の式より,部位1の原点(大腿の関節)に作用するトルク$${\bm{\tau}_1}$$は
$$
\bm{\tau}_1 = \left(\bm{I}_1 \dot{\bm{\omega}}_1 + \bm{\omega}_i \times (\bm{I}_1 \bm{\omega}_1) \right) + \left(\bm{I}_2 \dot{\bm{\omega}}_2 + \bm{\omega}_i \times (\bm{I}_2 \bm{\omega}_2) \right) +\\
\left(-{}_{g1}^{1}\bm{p} \times \bm{f}_{1} + {}_{g1}^{2}\bm{p} \times \bm{f}_{2} \right) + \left(-{}_{g2}^{2}\bm{p} \times \bm{f}_{2} \right) -{}_{g2}^{C}\bm{p} \times \bm{F} - \bm{\tau}_z
$$
となる.ここで,$${\bm{\tau}_1}$$は部位1の関節に作用するトルク(股関節トルク),$${\bm{f}_1, \bm{f}_2}$$は各関節(股関節,膝関節)に作用する力,$${\bm{F}}$$は床反力,$${{}^1_{g1}\bm{p}, {}^2_{g1}\bm{p}}$$は重心$${\bm{x}_{g1}}$$からみた各関節の位置ベクトル,$${{}^2_{g2}\bm{p}, {}^C_{g2}\bm{p}}$$は重心$${\bm{x}_{g2}}$$からみた関節$${2}$$とCOPへの位置ベクトルである.
これは「各部位の重心まわり」の運動方程式となっている.
ここで,$${\bm{f}_{2}}$$の項に注目すると,括弧単位で眺めた右辺の第3,4項の一部は
$$
{}_{g1}^{2}\bm{p} \times \bm{f}_{2} - {}_{g2}^{2}\bm{p} \times \bm{f}_{2} = {}_{g1}^{g2}\bm{p} \times \bm{f}_2
$$
と書き換えられる.図1をよく見てほしい.これは重心$${\bm{x}_{g1}}$$から重心$${\bm{x}_{g2}}$$への位置ベクトル$${{}_{g1}^{g2}\bm{p}}$$へまとめただけで,幾何学的に$${{}_{g1}^{g2}\bm{p} = {}_{g1}^{2}\bm{p} - {}_{g2}^{2}\bm{p}}$$を利用した.
さらに,合成のニュートン運動方程式から各関節に作用する力$${\bm{f}_1, \bm{f}_2}$$に関して
$$
\bm{f}_1 = m_1 (\ddot{\bm{x}}_{g1} - \bm{g}) + m_2 (\ddot{\bm{x}}_{g2} - \bm{g}) - \bm{F}\\
\bm{f}_2 = m_2 (\ddot{\bm{x}}_{g2} - \bm{g}) - \bm{F}
$$
を代入すると
$$
\bm{\tau}_1 = \left(\bm{I}_1 \dot{\bm{\omega}}_1 + \bm{\omega}_i \times (\bm{I}_1 \bm{\omega}_1) \right) + \left(\bm{I}_2 \dot{\bm{\omega}}_2 + \bm{\omega}_i \times (\bm{I}_2 \bm{\omega}_2) \right) - \\
{}_{g1}^{1}\bm{p} \times \left\{ m_1 (\ddot{\bm{x}}_{g1} - \bm{g}) + m_2 (\ddot{\bm{x}}_{g2} - \bm{g}) - \bm{F} \right\} + \\
{}_{g1}^{g2}\bm{p} \times \left\{ m_2 (\ddot{\bm{x}}_{g2} - \bm{g}) - \bm{F}\right\} - \bm{\tau}_z
$$
となるが,これを先程と同様に$${m_1 (\ddot{\bm{x}}_{g1} - \bm{g}),~ m_2 (\ddot{\bm{x}}_{g2} - \bm{g}), \bm{F}}$$に関する項で整理することで,最終的に
$$
\bm{\tau}_1 = \left(\bm{I}_1 \dot{\bm{\omega}}_1 + \bm{\omega}_i \times (\bm{I}_1 \bm{\omega}_1) \right) + \left(\bm{I}_2 \dot{\bm{\omega}}_2 + \bm{\omega}_i \times (\bm{I}_2 \bm{\omega}_2) \right) + \\
{}_{1}^{g1}\bm{p} \times(m_1 (\ddot{\bm{x}}_{g1} - \bm{g})) +
{}_{1}^{g2}\bm{p} \times m_2 (\ddot{\bm{x}}_{g2} - \bm{g}) - \\
{}_{1}^{C}\bm{p} \times \bm{F} - \bm{\tau}_z
$$
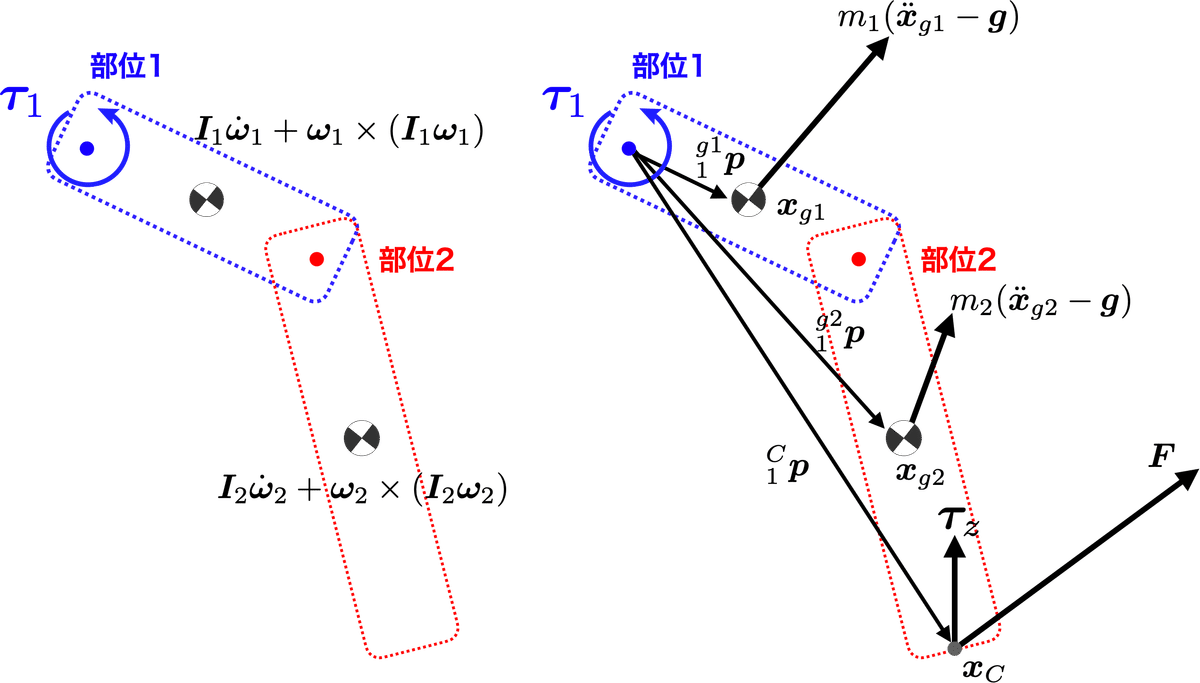
を得る(図3).ここで,$${{}_{1}^{C}\bm{p}}$$は部位1の原点(大腿の関節)$${\bm{x}_1}$$からCOP$${\bm{x}_C}$$までの位置ベクトルである.
右辺の第1,2項は各部位の回転の慣性力の項の和である.第3,4項は,部位1の「原点まわり」の並進の慣性力と重力に関する力のモーメントを表している.ダランベールの原理(d'Alembert's principle)から慣性力も力とみなすことができるので,これはわかりやすい式となっている.
また,力のモーメントの項は$${{}_{1}^{g1}\bm{p} \times, {}_{1}^{g2}\bm{p} \times, {}_{1}^{C}\bm{p} \times}$$のように全て,位置ベクトル$${\bm{X}_1}$$まわりの外積で記述されている.
この形式は,かなり見通しが良い.繰り返しになるが,計算したい部位の関節のトルク(この例だと$${\bm{\tau}_1}$$)は,慣性項($${\bm{I}_i \dot{\bm{\omega}}_i + \bm{\omega}_i \times (\bm{I}_i \bm{\omega}_i),~i=1,2}$$)と摩擦モーメント$${\bm{\tau}_z}$$を除けば,全ての力のモーメントが,部位$${1}$$の原点(股関節)まわりの力のモーメントの和で記述されている.具体的には部位$${1}$$の原点(股関節)からみて各部位の重心に作用する慣性力($${m_i (\ddot{\bm{x}}_{gi} - \bm{g}),~i=1,2}$$)と,COPに作用する外力$${\bm{F}}$$に関する三つの力のモーメントである.
以上で,2つの部位で構成される合成の回転の運動方程式は,回転の慣性力と根本の関節まわりの並進の慣性力と,同じく関節まわりの外力(床反力)に関する力のモーメントの和で表されることで示した.力のモーメントは全て「対象とする関節まわりの力のモーメント」という形式になっている.
もちろん3リンクになっても冒頭の式に示したが,同様に力のモーメントは全て一つの関節まわりの力のモーメントで記述でき(文献2),多体系の場合の一般化もジョルダンの原理(Jordain's principle)から導出が可能である(文献3).
このように一つの関節まわりの力のモーメントで記述されることから,モーメントアーム(てこの長さ)を考えれば,腕を振り回すときに,肩関節から見て遠い位置にある手先の質量が大きいと,肩の負担が大ききなることも,この式から説明でき,身体の先細り構造とこのことは決して無縁ではないだろう(補足2).
コードとしての合成の運動方程式
多体系で,関節に作用するトルクを計算するだけなら,これまで述べてきた漸化的ニュートン・オイラー・アルゴリズム(Recursive Newton-Euler algorithm)に基づく解法(このマガジンで述べた方法は,オリジナルのLuh, Walker, Paulの方法と解き方が若干異なるが,本質的には同じ)で計算するほうが効率が良いだろう.
一方,ここで述べるこの合成のオイラーの運動方程式は,漸化的方法のように部位ごとに逐次的に並進力と回転力を解くのではなく,一括して計算することができる.計算効率は劣るが,人によってはコードが書きやすいかもしれない.
身体運動における関節のトルクの意味
この式は,関節に作用するトルク(回転力)が,「運動によってどのように定まるか」を示している.そこで,少し視点を少し変えれば,この式から「床反力(外力)$${\bm{F}}$$を最大化するための身体を動かし方」と「その力を身体の目的の場所に効率よく伝達する動かし方」を考察できる.ここで目的の場所とは,ランニングや歩行であれば身体重心で,投球ならボール,ゴルフスイングならクラブヘッドと考えればよいだろう.
例えば,前述の例のように,走速度を高めるための数理的な必然性は「水平の床反力を大きくすること」に帰着する.このためには「重心の加速度の水平成分を大きくすること」が重要となる.これは地面と身体重心間で押し合うような,身体各部位の「おしくらまんじゅう」を行うことを意味する(図4).

身体部位間の「おしくらまんじゅう」を行う際,関節に作用するトルクがなければ,操り人形の支えがなくなり崩れ落ちるのと同様に,相互作用力は発生しない.このために筋肉というアクチュエータが必要となることが容易に想像できる.つまり,関節を動かすことではなく,むしろあまり動かさないほうが,大きな力が発生することも想像できるだろう.
回転の慣性力は小さい方が良い?
そのことを,もう少し数理的に考察する.
なお,外部環境と接する場合,環境と身体間には大きな並進の力を作用させることができるが,一般には環境と身体間にヒトが発揮できる回転力(トルク)は弱くなってしまう.たとえば手で道具を握ってても,手先が発揮できるトルクは弱く高々知れている.これは足部でも同様である.つまりトルクを伝達して末端にトルクとして伝えることは非常に困難という制約があることも念頭に置いてほしい.

すると前述の式を単純化し,水平面内を動く一つの梃子(link)と,その梃子に作用するトルク(力のモーメント)$${\bm{\tau}}$$と力$${\bm{F}}$$を考えてみよう(図5).すると関節軸まわりのこの梃子の運動方程式は,
$$
\bm{I} \dot{\bm{\omega}} = \bm{\tau} + \bm{r}\times \bm{F}
$$
となる.ここで$${\bm{I}}$$は慣性テンソル,$${\bm{\omega}}$$は梃子の角速度,$${\bm{r}}$$は関節から力$${\bm{F}}$$が作用する点までの位置ベクトルである.
ここで,力$${\bm{F}}$$を最大化する問題を考えれば,当然トルク$${\bm{\tau}}$$を大きくすることが必要となり,大きくなるほど$${\bm{F}}$$も大きくなるが,慣性力$${\bm{I} \dot{\bm{\omega}}}$$はただの抵抗負荷となるので,これは小さい方が良い.つまり,できるだけ加速度を発生しないように動かないほうが良いと言える.
同様に,これまで考えてきた多関節運動の場合でも,$${\bm{F}}$$を最大化する目的では,並進の慣性力$${m_i \ddot{\bm{x}}_i}$$や,回転の慣性力$${\bm{I}_i \dot{\bm{\omega}}_i + \bm{\omega}_i \times (\bm{I}_i \bm{\omega}_i)}$$でも,きるだけ回転の加速度を発生しないように動かないほうが,大きな力を関節に発生させるためには良いと言える.
また,もしこれらの慣性力がトルクや力のモーメントと比較して小さく
$$
|| \bm{I}_i \dot{\bm{\omega}}_i + \bm{\omega}_i \times (\bm{I}_i \bm{\omega}_i) || \ll ||\bm{\tau}_i || \\
||m_i {}_{i}^{gi}\bm{p} \times (\ddot{\bm{x}}_{gi} - \bm{g})|| \ll ||\bm{\tau}_i ||
$$
とみなせるなら,運動方程式は
$$
\bm{\tau}_1 \approx -{}_{1}^{2}\bm{p} \times \bm{F} - \bm{\tau}_z
$$
と近似的に書くことができ,動力学のように加速度,角加速度,角速度などの時間微分で記述することなく,力と姿勢の釣り合いだけでトルクを記述する静力学問題になる.

身体運動における比較:
ここから,実際のヒトの運動で比較を行う.ここで,図6のように股関節トルクと膝関節トルクを$${\bm{\tau}_1, \bm{\tau}_2}$$とし,床反力を$${\bm{F}}$$,地面と下腿間に作用する鉛直軸まわりの摩擦モーメントを$${\bm{\tau}_z}$$,股関節と膝関節からCOPまでの位置ベクトルを$${{}^C_1 \bm{p}, {}^C_2 \bm{p}}$$とすると,静力学近似の股関節と膝関節のトルクを
$$
\hat{\bm{\tau}}_1 \equiv -{}^C_1 \bm{p} \times \bm{F} - \bm{\tau}_z\\
\hat{\bm{\tau}}_2 \equiv -{}^C_2 \bm{p} \times \bm{F} - \bm{\tau}_z
$$
と定義する.これは例えば図2の上の式(再掲)の実際の股関節に作用するトルク
$$
\bm{\tau}_1 = \left(\bm{I}_1 \dot{\bm{\omega}}_1 + \bm{\omega}_i \times (\bm{I}_1 \bm{\omega}_1) \right) + \left(\bm{I}_2 \dot{\bm{\omega}}_2 + \bm{\omega}_i \times (\bm{I}_2 \bm{\omega}_2) \right) + \\
{}_{1}^{g1}\bm{p} \times(m_1 (\ddot{\bm{x}}_{g1} - \bm{g})) +
{}_{1}^{g2}\bm{p} \times m_2 (\ddot{\bm{x}}_{g2} - \bm{g}) - \\
{}_{1}^{C}\bm{p} \times \bm{F} - \bm{\tau}_z
$$
における,慣性力に関係する項
$$
\left(\bm{I}_1 \dot{\bm{\omega}}_1 + \bm{\omega}_i \times (\bm{I}_1 \bm{\omega}_1) \right) + \left(\bm{I}_2 \dot{\bm{\omega}}_2 + \bm{\omega}_i \times (\bm{I}_2 \bm{\omega}_2) \right) + \\
{}_{1}^{g1}\bm{p} \times(m_1 (\ddot{\bm{x}}_{g1} - \bm{g})) +
{}_{1}^{g2}\bm{p} \times m_2 (\ddot{\bm{x}}_{g2} - \bm{g})
$$
とトルク$${\hat{\bm{\tau}}_1}$$を分けて考え,慣性力に関する項が小さいとみなせる場合に,実際に作用するトルクと,この静力学近似のトルク$${\hat{\bm{\tau}}_1}$$が,実際どのぐらい近いか観察してみると,非常にラフな話で恐縮だが,静力学近似のトルク$${\hat{\bm{\tau}}_1, \hat{\bm{\tau}}_2}$$に対して,実際に作用するトルク$${\bm{\tau}_1, \bm{\tau}_2}$$を比較すると,たとえば,歩行やランニングの接地している股関節やゴルフスイング時の股関節では,約8割ぐらいの大きさで,膝関節では9割の大きさとなっている.
サッカーのキック動作における支持脚の例は文献2を参照していただきたいが,図7に近似のない股関節トルクベクトル$${\bm{\tau}_1}$$(赤)と,静力学近似によるトルク$${\hat{\bm{\tau}}_1}$$(緑)を,図8に近似のない膝関節トルクベクトル$${\bm{\tau}_2}$$(赤)と,静力学近似によるトルク$${\hat{\bm{\tau}}_2}$$(緑)を示した.


この結果は,近似を用いても,精度の低い画像解析やバターワースフィルタを使用して解析するレベルの精度は得られることを示している.
回転の運動方程式における慣性力の物理的意味:
このことからも,力を発揮する上で,身体を全く動かさないということはできないが,加速度が大きくならないように動かすことは可能で,もし床反力のような外力を,身体を通じて伝達する際には,ヒトは下肢をむしろ動かさないように(加速度を小さくするように)心がけて動かしていると考えて良い.
なお,とあるゴルフのコーチは「地面と押し合いながら,下肢だけでなく全身をアイソメトリックの状態に近づけるように」スイングすることが大切と形容されていたが,経験から導かれた言葉と思うが,そのような表現は的を得ていて面白い.
ちなみに,これは投球で大きな床反力を獲得し「ボールに伝達するにはどのように身体を動かせばよいのか?」,または「ゴルフスイングでスイング速度を上げるためには,どのように身体を動かせばよいのか?」という問いと共通する.ランニングでは床反力は身体重心に並進力を作用させることになるが,スイング運動ではそれを手先に伝達する問題に置き換わる.
ただし,腕やクラブなどの末端では,高速に運動するので下肢や体幹で生成した大きな力やエネルギーは,上肢で慣性力として大量に逃げてしまうことは避けられない.
トルクは姿勢で一意に定まる
冒頭述べたように,床反力のような外力が大きく作用する部位近く(例,地面と接する支持脚)では,図9のように運動をしている最中でも
$$
\bm{\tau}_1 \approx -\bm{r}_1 \times \bm{F} - \bm{\tau}_z \\
\bm{\tau}_2 \approx -\bm{r}_2 \times \bm{F} - \bm{\tau}_z
$$
の関係が成り立つということは,トルクは外力ベクトルと,力が作用する位置と,関節の位置ベクトルで定まるので,関節の位置などの姿勢が重要であることを示している.ここで,全て片脚(左脚)を対象とし,$${\bm{F}}$$は床反力$${\bm{\tau}_1, \bm{\tau}_2}$$は股関節と膝関節に作用するトルク,$${\bm{r}_1, \bm{r}_2}$$は股関節と膝関節からCOPまでの位置ベクトルである.

たとえばスクワットや垂直跳びで,股関節が重心より大きく後方にあれば,股関節のトルクが大きく発揮され,膝関節が重心よりも大きく前方に位置していれば,膝関節のトルクが大きくなるであろう.
このことを静力学的近似の式を使って説明する.たとえば股関節に作用するトルク$${\bm{\tau}_1}$$は$${ -\bm{r}_1 \times \bm{F}}$$で記述されるが,外積の意味を考えると,これは薄い青色の四角形の面積で定まる.これが主としてCOPと股関節間の水平距離に影響を受けることを考えれば.膝関節のトルク$${\bm{\tau}_2}$$は,図9の姿勢では膝とCOPの対角線で構成される四角形の面積(薄赤色)は小さく,$${\bm{\tau}_2}$$が小さくなることが
わかるだろう.
「計算ツールの視点」からのこのようなトルクの式の意味と,外積を理解していれば,「床反力ベクトルと姿勢」で,どこの関節に負担がかかっているかが容易に想像がつくはずである.冒頭に述べたが,外力が支配的な状態では股関節のトルクを定めるには,膝の位置は関係ない.股関節とCOPの位置(姿勢)と床反力ベクトルで一意に定まる(計算できる).
外力$${\bm{F}}$$とトルク$${\bm{\tau}}$$の関係は,姿勢で関係づけられ,その姿勢を定めるヤコビ行列$${\bm{J}}$$で記述すると冗長性との関係から明確になるが,詳細は文献4などをご覧になるとよいだろう.
ACL損傷の研究への応用
このような静力学近似の計算は,ACL損傷のメカニズム解明や障害予防にも寄与している.ここでの示した飛び降り後のバランス運動のような動作を用いて,上記の評価方法を持ちてACL損傷のリスク評価にも応用されている.
下腿の長軸まわりのトルクのほとんどがACLに対して負担のかかるトルクとして考えると,着地時の姿勢でACL損傷のリスク評価が可能となる.
ご興味ある方は,文献5,6,7などを参照されたい.
vs トルクの関節運動還元主義
ここで重要なことは,近似して関節に作用するトルクを計算できるという事実もさることながら,なぜ,そのような制御をヒトが行っているかである.
多くの人の関節運動に対するイメージは,関節に作用するトルクを大きく発揮することで,関節まわりの身体部位を速く動かすことができ,トルクの大きさ観察すればパフォーマンスの良し悪しを観察できると考えているのではないだろうか.一般的に,エリートアスリートほど筋力が強いことは間違いないし,多くのアスリートはそのようなトレーニングを積んでいる.そして,たしかにヒトの駆動力は関節レベルではそこに作用するトルク以外になく,それが身体を動かす唯一の動力源である.これは間違いない.
すると,その駆動力が作用する関節まわりの部位を動かすことで,身体全体の動きを形成していると考えるのが自然である.ロボットの運動の設計(軌道計画問題)でも,どちらかというとそのような思想である.手先の軌道を決めて,それを逆運動学で関節に分配し,そこから関節駆動力を逆動力学計算のよって計算するという流れである(補足3).
しかし,意外とそんなことをヒトは行っておらず,ヒトは(速く)末端を動かすために,腰などを回すことなどどうでもよく,恐らく力を身体の他の部位に伝達することで,つまりむしろ関節を動かさないような制御を行なっているというのが,ここでの「主張」なのだが,ここで長々とこれ以上述べるははばかれるので,この程度にとどめておく.
動かして学ぶ関節のトルクの計算と意味
これまで示してきたデータは,台から片足で飛び降り,着地後のバランス運動を観察してきた.このタスクでは角速度も角加速度も小さく,接地側の下肢の慣性力が小さいことが十分予想ができる.このバランス動作で,どのぐらい慣性力が小さいのかを確認する.
いつものように以下のGoogle Colaboratoryのリンクから,ブラウザでPythonコードを実行できるようにした.なお,ログインするためには,Googleアカウントが必要となるので注意をされたい.
また,使用するモーションキャプチャのサンプルデータ(sample_optitrack_221027.csv)は,このリンクからダウンロードして,Google Driveをマウントし,マウントしたドライブにそれらをコピーしてご使用いただきたい.これは,第6〜12章で使用したデータと同じであるので,すでにダウンロ度済みの方は,サイドダウンロードする必要はない.
なお,Google Colaboratoryの使用方法は,
を参照されたい.
図10は以下のコードによって,
t_list = np.arange(len(b_link[10].tau_global))/360.
len_data = len(b_link[10].tau_global)
tau_z = np.vstack([np.zeros(len_data), np.zeros(len_data), b_link[12].ext_moment[:,2]]).T ## friction moment vector
plt.plot(t_list, b_link[10].tau_global)
[plt.plot(t_list, (-np.cross(cop - b_link[10].p, b_link[12].ext_force)-tau_z)[:,i], linestyle='--', c=['b','r','g'][i]) for i in range(3)]
plt.xlim(2.5, 5.8)
plt.ylim(-300,385)
plt.xlabel('Time [s]')
plt.ylabel('Torque [Nm]')
plt.suptitle('Moment of hip joint')
plt.legend(['Tx', 'Ty', 'Tz', 'hat_Tx', 'hat_Ty', 'hat_Tz'])
股関節で近似なしの股関節に作用するトルク$${\hat{\bm{\tau}}_1}$$(実線)と,静力学近似で計算したトルク$${\hat{\bm{\tau}}_1}$$(破線)を比較したものである.
同様に,図11に膝関節に作用するトルクにおける比較を示した.

股関節と膝関節作用するトルクを比較すると,近似間との差は股関節のほうが大きく,これは大腿の質量が大きいことが影響していると考えられる.
また,実線と破線の差はほぼ
$$
{}_{1}^{g1}\bm{p} \times(m_1 (\ddot{\bm{x}}_{g1} - \bm{g})) +
{}_{1}^{g2}\bm{p} \times m_2 (\ddot{\bm{x}}_{g2} - \bm{g})+
{}_{1}^{g3}\bm{p} \times m_3 (\ddot{\bm{x}}_{g3} - \bm{g})
$$
で占められており,回転の慣性力はほぼ0に近い.これは,度々述べてきたように大きな力を伝達するためは,重い部分ほど加速度が小さくなるようにという意味で動かないことが重要であることを示している.
なお,ここでは示さなかったが,Google Colaboratoryのファイルでは,この重心に作用する慣性力と重力の和$${m_i (\ddot{\bm{x}}_{gi}-\bm{g})}$$をLinear_Inertial_force()関数を使用して計算し,上に示したその力のモーメントの大きさや,回転の慣性力$${\bm{I}_i \dot{\bm{\omega}}_i + \bm{\omega}_i \times (\bm{I}_i \bm{\omega}_i)}$$を関数Inertial_Force_global()で計算し,それをインスタンス変数inertial_globalに格納されているので,その大きさが確認できる.他に便利な関数もコードもあるので,ご自身でいろいろと計算し確認をしてみてはいかがであろうか.
おわりに
冒頭述べたように,合成の運動方程式には二つの観点から重要な意味を持つ.ひとつは関節に作用するトルクの計算方法として意味の見えやすい形式を利用し,さらに静力学的な近似式に落とし込めば外力が作用する近傍の部位では,ただのトルクは釣り合い式で計算できるという性質である.単に正確にトルクを計算するのであれば,ここで述べた合成の運動方程式を用いる必要はない.しかし,たとえば支持脚の股関節以下のように,外力が作用する部位近くでは,近似的に関節に作用するトルクを計算できる.
ただし,この近似はヒトが目的のある行動を行っている際に,常に効率よく運動を行っているときだけに成立する近似でである.しかし,恐らくヒトはほとんど例外なく,そのように運動を行わないと身体運動としては成立しないといって過言ではないぐらいの強い拘束であり,生命的な必然性だろう.そのような制御は考えず,安定性ばかり追求するロボットでは果たしてどうだろう?
すべての運動で検証したわけではないが,外力が作用する場合,恐らくほとんどの運動でいわば「動かずに,動かす」という戦略が用いられていると思われる.なお,この「動かさず」というのは,特に質量の大きな部位や,力を生成している部位近くで主にあてはまり,その力を伝達して「動かしたい部位」は離れていることを意味している.
これは筋肉のダイナミクスとも関係している.筋肉は高速な運動を行っている際に,外力を発揮したくても,自分自身を収縮することにエネルギーを使用してしまい,筋肉の外に力を発揮する余力がなくなるという粘性的な性質を持ち合わせている.このため,大きなエネルギーを発揮するためには収縮速度は遅いことが望ましいこととも密接に関係していると考えられている(文献8).
次回
次章ではステックピクチャを動かすコードを示していく.
補足
補足1:力のモーメントとトルク
筋力(駆動力)の発揮によって生じる関節に作用するトルクを,スポーツバイオメカニクスで一般的な関節トルク,またはロボットで呼ばれている関節駆動力(一般的かどうかわからないが古い教科書では多く使用されている)呼べばよいのだが,ここではバイオメカニクス以外にロボティクスやエンジニアも読者の対象として想定しているため,まわりくどいが,意味を明確にするために関節に作用するトルクと呼ぶこととした.
なお,トルクと力のモーメントは,単位も同じNmで,同じ回転力として機能するが,ここでは偶力と同様に回転の中心(原点)に依存しない回転力をトルク,回転の中心に依存する回転力を力のモーメントと呼んでいる.
アクチュエータであるモータや筋力が発揮するトルクは座標系に依存しないため,実際にはそれらが作用する関節(回転の中心)が存在するが,回転の運動方程式では,もはやどこに作用するかは関係なく,力作用点や回転の半径を考える必要がない物理量である.
一方力のモーメントは,関節に作用する並進力と,回転の中心(原点)を想定して計算し,原点に依存して値が変わる物理量であることに注意されたい.
偶力が回転の中心に依存しない物理量である理由は
を参照されたい.
補足2:先細り構造
外力が作用する部位近くでは特に,ヒトは慣性力を小さくするように運動すると述べたが,これは昆虫や恐竜,マジンガーZではおおきく事情が異なってくるかもしれない.もちろん確認はしていないが,質量や慣性モーメントの小さい昆虫では,激しく動いても恐らく他の外力と比べて慣性力はそれほど大きくならないことが予想され,羽ばたきなどの高速な運動を行ってもそれほどエネルギー消費は大きくないのかも知れない.
一方,大型の恐竜やマジンガーZを制御する場合,慣性が大きすぎて,少しでも激しく動かすとそれは相当なエネルギー消費をもたらすことが予想される.地球の重力下では相対的にアクチュエータの質量が重すぎるだろう.昔にタイムスリップできないので検証はできないが,CGや映画などでよくみるように獰猛な恐竜が激しく機敏に走ることは恐らくありえないだろう.肉食恐竜がどうやって捕食するのかまでは想像ができないが,ゆったりとしか動けないに違いない.空想もほどほどにと思う次第である.
補足3:トルクの関節運動還元主義
トルクのが大きいことがその関節まわりの部位を速く動かすことに直結し,トルクの大きさ観察すればパフォーマンスの良し悪しを観察できると考えがちである.このような考え方を,ここではトルク還元主義と呼ぶことにする.これはヒトではあまり成立しておらず,特にスポーツのような外力が強く作用する場面や部位では顕著である.
たしかに,関節レベルで最小の自由度で記述するラグランジュの運動方程式を考えれば,ヒトの運動の駆動力は関節に作用するトルク以外になく,それを支えるアクチュエータである筋力が動力源であることは間違いないのだが,それが直接そのまわりの部位を動かすように作用するのではなく,ここで示した事実は,骨格系を利用して少し離れた部位の運動に寄与するように動かしていると考えることができそうだ.
参考文献
1)杉原,ロボット工学に基づく二足歩行制御の構成論的理解,第75回 ロボット工学セミナー 歩行の生理学/力学/制御理論と歩行支援ロボティクス,2012.
2)西川ら,ヤコビ行列を用いた静力学による着地動作解析,シンポジウム: スポーツ・アンド・ヒューマン・ダイナミクス講演論文集,108, 2013
3)太田ら,Jourdainの原理に基づく逆動力学解析に適した全身の運動方程式の導出,シンポジウム:スポーツ工学・ヒューマン・ダイナミクス,C1,2015
4)伊藤,身体知システム論(ヒューマンロボティクスによる運動の学習と制御),共立出版,2005
5)小笠原他,静力学を用いた膝前十字靭帯損傷のリスク評価,ジョイント・シンポジウム講演論文集:スポーツ工学シンポジウム:シンポジウム:ヒューマン・ダイナミックス,B-2, 2009
6)Ogasawara, et al., Rearfoot strikes more frequently apply combined knee valgus and tibial internal rotation moments than forefoot strikes in females during the early phase of cutting maneuvers, Gait & Posture, Vol.76, Pages pp.364-371, 2020
7)Ogasawara et al., Effect of Rearfoot Strikes on the Hip and Knee Rotational Kinetic Chain During the Early Phase of Cutting in Female Athletes, Sports Medicine, Vol.7, 75, 2021
8)小林一敏,スポーツの達人になる方法(テクノライフ選書),オーム社,1999



【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
