
IMUによるモーションセンシング #2 〜加速度センサは力センサである〜
IMUを構成する加速度センサとジャイロセンサ.このうち加速度センサはバイオメカニクスではそれ以上の意味を持つ.ここでは,身体運動の計測を意識し,その特性について述べていく.
ここで,もっとも注意すべきは,加速度センサは加速度を計測するセンサとして捉えがちだが,その本質は加速度に作用する力を計測するセンサであるということだ.加速度線センサは実は加速度を計測するセンサではないと述べるとギョッとするだろうが,さほど間違いではない.理解せずに加速度センサを利用すると,かなり痛い目にあうので注意されたい.
そもそも加速度とは?
物理やバイオメカニクスを学んでいる方に,いまさら加速度(acceleration)の説明は不要だろう.ここでは専門でない方を対象に加速度の物理的意味を考える.理解している方は,この節「そもそも加速度とは?」を読み飛ばしていただいてよい.
速度や加速度の理解に,時間微分(time-derivative)の概念は欠かせない.しかし,微分を教えずに速度や加速度を教える高校物理の教科書で,微分の説明の本質は,時間による割り算である.しかし,このような説明で加速度が,直感的に理解しやすいかどうかはやや疑問である.どうやって計算するかにこだわらなければ,単純に,微分を位置や速度(velocity)のグラフの傾き(勾配)として説明するほうが物理的意味を捉えやすいと考えている.そこで,本質的には同じだが,差分(割り算)によって説明するかわりに,グラフの「接線の傾き(勾配)(gradient)」によって微分を試みる.
「加速度とは?」との問いに対する筆者の回答を簡潔に先に述べておこう.速度が変化するときに加速度が発生するが,「加速度とは速度の単位時間あたりの変化」であり,グラフにおいては「加速度とは速度曲線の接線の傾き」である.以下で,もう少し詳しく加速度の説明を試みる.
加速度とは速度変化の傾き
時間変化が一定の例:
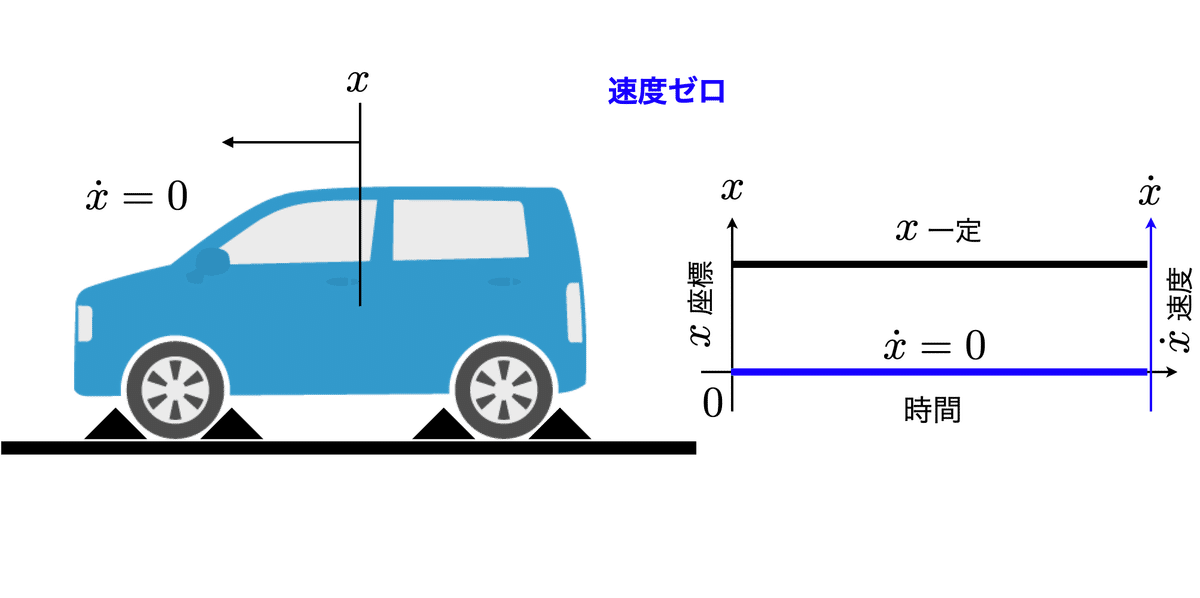
・動かない場合
図1は自動車止まっている例を示しているが,このように「位置の変化がない」(図1の黒線)ことは「速度がゼロ」(青線)であることを示している.物体の位置が同じところにとどまっていれば(図1のように自動車が停車していれば),「位置の変化がゼロ($${x}$$一定)」=「速度がゼロ($${\dot{x}=0}$$)」を示している.
・等速運動
もし位置が少しでも変化するとき,その「位置の変化の割合」が速度(velocity)で,自動車の$${x}$$座標が動いていれば,自動車は速度を持つことになる(図2).速度($${\dot{x}}$$)とは,$${x}$$座標の変化で,それはグラフの$${x}$$の傾きで表す.図2の例は$${x}$$座標が一定の傾きなので,速度$${\dot{x}=v}$$の一定のグラフとなる.この傾きが大きいほど,速度が大きいことを示す.

・等加速度運動:
次に,位置の変化のかわりに速度の変化を考え,「一定の速度(速度変化がない)」は「加速度がゼロ」であることを示す.図2のように物体の速度$${\dot{x}}$$が一定であると(たとえば自動車の速度メータが大きくても小さくても一定であれば)それは等速運動で,「加速度はゼロ」となる.
もし速度$${\dot{x}}$$に少しでも変化があると,加速度($${\ddot{x}}$$)を持つことになる.つまり,速度の変化が加速度(acceleration)である.図3の例は,速度$${\dot{x}}$$が一定の傾きなので,加速度$${\ddot{x}=a}$$の一定のグラフとなる.これを等加速度運動と呼び,重力加速度による自由落下運動はその一例である.速度変化の傾きが大きいことは,加速度が大きいことを示す.加速度は速度の傾きの大きさである.

もし,自動車の速度がだんだん(急に)大きくなったり,小さくなるなどの変化があれば,自動車は加速度を持つことになる.位置の変化率が速度で,速度の変化率が加速度と考えればよい.ここでは速度や加速度が一定の場合を考えたが,次に,速度や加速度が一定でなく変化する例を考える.
ちなみに,その速度変化(傾き)が加速度であるが,速度変化をもたらす実態は力(force)である.
時間変化が複雑な例:
位置や速度が一定ではない例を図4に示す.この例では速度(青色)がゼロから最大値を迎え再びゼロに近づいている.このとき,速度の極大値では,速度曲線の接線(黒)の傾きは平らでゼロとなる.このためその時の加速度(赤)はゼロとなる.またその少し手前の速度の傾きが最大になるところで,加速度が極大を迎えていることがわかる.このように「速度曲線の接線の傾きが加速度」であることを示している.
また,このように速度の極大値の時間的に手前で,加速度の極大を迎える.つまり,加速し終わったあとに速度が最大を迎える.このことは積分で説明ができるのだが,説明はこの程度にとどめておく.

さらに複雑な速度・加速度変化の例として,図5にゴルフクラブのヘッドの速度,加速度のグラフを示す.

図5は,横軸が時間をしめし,インパクトが時間0 [s]となるように示している.グラフはトップと呼ばれるスイング開始から〜インパクトまでの時間を示し,縦軸の左の青線が速度で,右の赤線が加速度を示している.
速度カーブの極大,極小となっているところでは,速度カーブの傾きが平ら(ゼロ)であるので,傾きを表す加速度はゼロとなる.一方,速度の傾きが極大(最大)となるところでは加速度が極大(最大)となっている.このように速度曲線の接線(黒線)の傾きが加速度を示している.
この「傾き」とは速度が変化する割合を示していて,この傾きが大きいということは単位時間あたりに速度が変化する割合が大きく,加速度が大きいということを示している.このことから加速度が大きいということは,速度が大きく変化することを意味する.
なお,ゴルフスイングではおおよそインパクト付近で最大値を迎え(実際には僅かであるがインパクト後に速度の最大値を迎えるようなスイングをしていることが多い.この例ではインパクト近辺はノイズで加速度の計算が乱れているが,インパクトではわずかに速度は上側に傾いている),加速度がインパクト近辺でゼロとなる.
このように,幾何学的にグラフの曲線の傾きを求めることが,数学の微分(diffentiation)に相当する.言葉で述べれば時間変化(time change, time variation)や時間変化率(time rate of change)と言える.
繰り返しなるが,ここで重要なことは,「速度変化をもたらすもの」は力(force)である.また,速度の変化が加速度だが,力と加速度は物理的意味が異なる.身体のような複雑な構造をもつ場合,計測した加速度に質量をかけたものが,単純に力とはならないことに注意されたい.力と加速度は運動方程式を介し関係が記述される.
なお,加速度の中には名前がついたものがある.たとえば重力加速度(gravitational acceleration)は,重力(gravity)という地球上の力がもたらす加速度である.地球上でほぼ一定であるが,地球が引張る引力は地球の中心方向(鉛直下方)を向き,この他に地球の時点による回転などの効果などで重力が定まる.地球上ではおおよそ一定であるが,正確には岩盤の厚さや緯度などによって変化する.膨らんでいる赤道近辺では自転軸から距離や方向の効果で,極付近と比較し若干(0.5%程度)小さくなる.なお,理科年表などによれば東京では9.798,福岡では9.796 [m/s^2]である.
単位
速度は座標(位置)の時間微分であるが,位置の時間変化曲線の接線の傾きであることから,位置を時間で割ることから速度の単位は
$$
\frac{\text{m}}{\text{s}}
$$
となり,加速度の単位は速度の時間微分であり,加速度の計算のためにはもう1回時間での割り算を行うので,
$$
\frac{\text{m}}{\text{s}^2}
$$
となる.またIMUが出力する加速度の単位としては$${\text{G}}$$(ジー)が用いられることが多く,先ほど示したようにこれは重力加速度を基準とした単位である.物理計算を行う際には, 9.8 をかけるなどして,単位を[m/s^2]にする必要がある.なお,場所によって加速度は異なると述べたが,重力加速度に強く依存する,よほど高精度な計算を行うときを除けば,9.8や東京の9.798,福岡の9.796 [m/s^2]の違いはさほど気にしなくて良い.多くの計算ではそれ以外の誤差要因のほうの影響が大きいのではないだろうか.
加速度センサは力センサである
加速度センサはその名のとおり加速度を計測するセンサとして考えがちだが,むしろこれは力を計測するセンサとして考えたほうがよい.このことを以下に説明する.
計測原理
第1章
では,加速度センサは直接的には重りを支える梁に作用する力を計測すると述べた.つまり,ここで加速度について説明したばかりで恐縮だが,加速度センサはどちらかというと加速度を計測するセンサとして考えるよりも,一種の力センサと考えるのが良い.

図6は,このセンサの向きの場合,上下方向を計測するための,1軸のひずみゲージ型加速度センサの内部構造のイメージである.筆者も分解して中を除いたことはないが,内部には梁でささえられた重りがあり,梁にはひずみゲージが貼られている.このひずみゲージは,梁のたわみを計測しているが,たわみは計測方向に作用する力に起因するたわみと,重力に起因するたわみを計測する.
このとき,加速度センサに力$${\bm{f}}$$が作用しているときの,質量$${m}$$の重りの運動方程式は
$$
m \ddot{\bm{x}} = \bm{f} + m \bm{g}
$$
となり,加速度センサは直接的にはこの加速度センサに作用する力
$$
\bm{f} = m (\ddot{\bm{x}} - \bm{g})
$$
を計測する.つまり一種の動く力センサである.一般に物体に作用する力を計測する力覚センサは「固定して」動かさずに(そもそも動いては計測原理が成り立たない),力覚センサに作用する外力を計測する.ところが,加速度センサは動いている物体(加速度センサ)に作用する外力を計測するところに特徴がある.図6の構造を考えれば理解だろう.また,センサの計測原理に依存するが,ひずみゲージ型のような加速度センサは,重力を含んだ力を計測するところにも特徴がある.
ここで,センサの重りの運動方程式を成分で考えると,
$$
m (\ddot{\bm{x}} - \bm{g}) \\=
m \left( \begin{bmatrix} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{bmatrix} -
\begin{bmatrix} 0\\0\\-g\end{bmatrix}
\right)
\\ =
m \begin{bmatrix} \ddot{x} \\ \ddot{y} \\ \ddot{z}+g \end{bmatrix}
$$
となる.ここで,加速度は$${\ddot{\bm{x}} = [\ddot{x}~\ddot{y}~\ddot{z}]^T}$$の成分を持つとした.
もし,鉛直上方の向きを計測方向とする1軸の加速度センサがある場合,この1軸センサは運動方程式のうち,$${z}$$軸成分の計測信号$${m(\ddot{z}+g)}$$を出力することになる.
このように,固定された物体に作用する力を計測する力覚センサと異なり,加速度センサは動く物体の運動方程式そのものを計算するセンサである.重力加速度まで含んでいるので,このまま加速度センサの信号で力学計算が可能となる優れものだ.
反対に常に重力加速度を含んだ出力をするので,加速度だけを検出する際には厄介である.また,センサに固定された座標系の信号を出力するので注意されたい.
MEMSセンサの計測原理
大きさは1cmほどであるが,ひずみゲージ型加速度センサは非常に精度の高いセンサである.これに対して第1章
で述べたMEMS型の加速度センサも,色々なタイプがあるが,基本的には重りと梁の構造を有し,その変形を測ることでセンサに作用する力を計測していることには違いがない.

図7にはMEMS加速度センサの内部構造のイメージを示した.図1と構造は異なるが,基本重りに作用する力を梁のたわみで計測している点では同じで,ひずみゲージ型加速度センサは,ひずみ(ストレイン)アンプで計測しているが,MEMSでは静電容量などで計測している点が異なる.
なお,重力加速度を含むため運動方程式を解く上では好都合だが,キャリブレーションなどの際には,鉛直方向に重力加速度を含むため注意が必要で,純粋に加速度計測を考えた場合,重力加速度を除去する必要があるので面倒である.このような意味で,加速度センサの素直な利用方法は動力学計算といえる.
そもそも加速度センサはセンサに作用する力を計測する
加速度センサは,もちろん加速度を計測するセンサではあるが,どちらかというとセンサに作用する力センサであるという認識を持つ方が良い.3次元空間を回転しながら自由に動く加速度センサから,純粋に重力加速度を除いた運動に起因する加速度だけを抽出するのは結構面倒な計算が必要だ.それについては,どこかで述べていく.
加速度信号の符号の問題点
センサは運動の加速度と反対向きの加速度を出力する(符号が反転する)

加速度センサを使っているときに混乱を与えるのが,信号の符号(向き)である.まず重力によって引っ張られる重力加速度だけ考えてみる.たとえばセンサの計測方向を上向きに置いた時,重力は下向きに重りを引張る.すなわち力が鉛直下方に作用し,図8のセンサ内部では重りは下側にたわむ.このとき重力加速度によってセンサの信号は「負」の信号を出力する.これは加速度センサとして考えると正しい出力である.
ところが,センサ計測方向の正の方向,すなわち鉛直上方にセンサを加速すると,同様にセンサの重りは下側にたわむ(図8左).このためセンサの運動の加速度が反対の上向きに運動しても,重りは同じように下側にたわむ.つまり,運動の加速度の向きとは反対方向に加速度センサの信号が出力される.これは,前述のように加速度センサが「力を計測する」ことに起因する.このことは後述の運動方程式でも示される.直感と異なるかもしれないが,運動による加速度と重力加速度の向きが下向きと同じでも(図8右),一般にはセンサは重力方向に合わせているので,加速度信号の向きは重力加速度と運動による加速度の向きは反対方向になることに注意されたい.
つまり,重力加速度の向きは正しく出力するのに対して,運動による加速度によるセンサの出力の向きは反転し,誤った出力を行う.これはセンサのチップ自体の仕様である.ほとんどのメーカーのセンサチップがそのような仕様となっている.何も運動をしていないときには重力加速度しか作用しないが,センサを下向きにしたときに+1Gを指すのが,直感的と考えたからなのかもしれないが,物理的には反対であるので,運動による加速度を計測する際には,加速度の符号を反対にしてご利用いただきたい.
運動方程式による考察:
このことを運動方程式で考えてみる.センサの重りの運動方程式は
$$
m \ddot{\bm{x}} = \bm{f} + m \bm{g}
$$
となる.ここで,$${m}$$はセンサ内部の重りの質量,$${ \bm{x]}$$は重りの位置ベクトル,$${\bm{f}}$$はセンサに作用する力ベクトル,$${\bm{g}}$$は重力である.
このとき,Z軸方向の加速度センサの運動方程式は
$$
m \ddot{z} = f_z + m(-g) \\= f_z - mg
$$
となる.$${z}$$はZ軸の座標,$${f_z}$$はセンサに作用するZ軸方向(鉛直上方の)力成分,$${g}$$は重力加速度である.重力加速度は下向きに作用するので重力$${mg}$$の符号はマイナスである.するとセンサの出力である$${f_z}$$は
$$
f_z = m (\ddot{z} + g)
$$
となる.もしZ軸の上向きに加速するなら,$${m (\ddot{z}}$$も$${mg}$$も正の向きを示しているので,加速度センサの出力は正となるべきだが,前述のように実際のセンサの出力は反対の負であることに注意されたい.つまり,加速度センサの出力$${a_z}$$は,見かけ上,質量で割り算したとし,符号が反転するので,
$$
a_z = - (\ddot{z} + g)
$$
を出力する.
また,これが,重力の向きと力や加速度の向きが反対に出力される理由で,前述のように加速度センサが力を計測するセンサであることに起因する.
そして,繰り返し述べているが,加速度センサは常に重力加速度を計測している.
よく考えないと,計測する信号の意味を見失うので注意されたい.このような注意点は,他ではほとんど説明されていないだろう.
例題:
もし,加速度センサのZ軸の正の方向を,鉛直上方に向けたまま,センサを上向きに+1 [G]で加速し続けたとしよう.このとき加速度センサのZ軸はどのような信号を出力するだろう?
1.2 [G]
2.-2 [G]
3.ゼロ
答えは,2の-2 [G]である.図8左を考えれば,すぐに分かるだろう.
では,例題と同じようにセンサの検出方向(正)を上向きにしたまま,自由落下させてみよう(妄想),センサはどのような信号を出力するだろう?
答えは述べない.回答に自身が持てないようなら,もう一度記事を読んでいただければと思う.ただし,答えは最後の$${a_z}$$の式の$${\ddot{z}}$$に適切に値を代入を行えば良いだけだし,図8右を考えればわかるだろう.
この結果から,読者は,加速度センサが「加速度を計測するセンサ」だと述べてよいと思うだろうか?



【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
【データの計測について】
スポーツセンシング社のスタジオで,フォースプレートやモーションキャプチャを利用した計測も行えます.出力されるデータと,ここで示したプログラム(入力データの取り込み関数を少々改変する必要があるが)で,同様な解析を行えますので,まずはお気軽にお問い合わせください.
