
動かして学ぶバイオメカニクス #21 〜関節のインピーダンスの可視化〜
こでまでのエネルギーに関する議論では,エネルギーの流れを可視化し(第16章),さらにその流れを構成する力ベクトルと速度ベクトルに分解した(第18章).第19章ではエネルギーの流れを構成する力と速度から,流れの抵抗(インピーダンス,力と速度の比)を導入した.ここでは,実際の運動中の力と速度の関係図を示す.
はじめに
たとえばボールなどの速度を増加させることは,ボールの力学的エネルギーを増加させることを意味する.力学的エネルギーは重力によるポテンシャル(位置)エネルギーと運動エネルギーの和であるが,投球ぐらいになればポテンシャルエネルギーは無視して良い程度の小ささであるから,運動エネルギーが速度の二乗に比例する.したがって,線形(比例)ではないがボールの力学的エネルギーの増加は速度の増加と関係すると考えて良い.
その力学的エネルギーの時間変化(時間微分)は,手先からボールに作用する力ベクトルとボールの速度ベクトルの内積と,トルクベクトルと角速度ベクトルの内積で定まるが,これらをここではエネルギーの流れと呼んでいる.力学の教科書にはこのエネルギーの流れの記述はないが,工学的には電気的エネルギーや流体の流れのエネルギーとのアナロジーから,流れと呼ぶことは自然である.
したがってボールの速度を増やすにためには,単位時間あたりのボールへの力学的エネルギーの流れを増やすことが肝心となる.幸い,この力学的エネルギーの流れは,力ベクトルと速度ベクトルに分解することができ,そこから多様な議論が可能となる.
たとえば,ボールに流入させるエネルギーの流れを増やすためには,ボールに作用する力ベクトルと速度ベクトルの内積を増やすこととなるが,その動力源は手ではなく,下肢や体幹や肩まわりの筋群で,それらは伝達されてボールに届くことになる.つまりエネルギーの伝達や流れを効率よくすることが,ボールの速度増加と密接に関係する.
また,力と速度で記述されるボールの状態は時々刻々変化し,加速し始めはボールに作用する力が大きい割にはボールの速度が小さく,リリース時にはボールに作用する力が弱いが速度は最大近くとなることにも留意すべきである.
この力と速度の比を機械的インピーダンスと呼び,これはエネルギーの流れの抵抗に相当し,それは時々刻々変化するのに対して,動力源である筋肉の機械的インピーダンスはそれほど変化しない.一定とみなして良いだろう.
そこで,単位時間あたりのエネルギーの流れを最大化し,筋群からボールにエネルギーを効率よく伝達するためには,梃子によるパワーマッチングが重要であることを第19章で述べた.
そこで,身体運動における最適なマッチングの証拠を見せることはできないが,この章では関節レベルでインピーダンスの状態を観察することを試みる.
関節と筋の力学特性
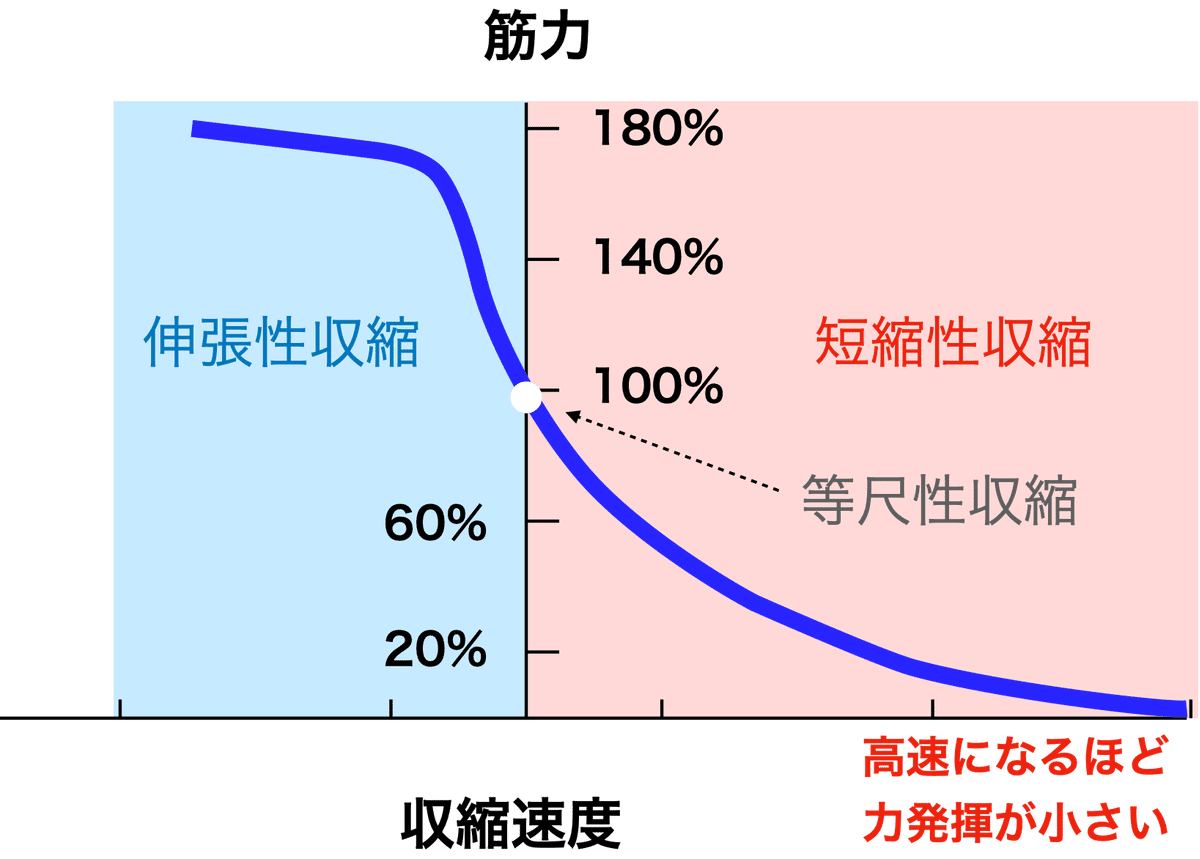
筋肉の収縮力(筋力)と収縮速度の関係は図1のような関係となることをこれまでも示したが,これはあくまでもカエルの摘出筋の実験結果からなどのイメージ図である.実際のヒトの筋肉の力–速度関係の同定は困難で,恐らくヒトの推定例もないだろう.伸張性収縮の曲線が本当にこのようになっているかは,実際のところわからない.
ただし,最大努力で行ったり,最大負荷が作用しているとは限らないが,運動中の筋力と収縮速度の計測や推定は行われてきているようだ.
いずれにせよ,「筋レベル」でこのような力–速度特性を調べるのは困難だが,これを「関節レベル」で間接的に調べることは若干ハードルが低い.このことを以下で簡単に説明する.
筋力と関節に作用するトルクは,

図2のようにモデル化し,筋張力$${\bm{f}}$$が作用する方向と関節間の距離を$${\Delta r}$$とするなら,筋張力$${\bm{f}}$$がもたらす関節に作用するトルク$${\bm{\tau}}$$は
$$
\bm{\tau} = \bm{r} \times \bm{f} = \Delta r ~|\bm{f}|
$$
となる.$${\Delta r}$$はモーメントアームに相当するが,実際の関節構造は複雑であるために,$${\Delta r}$$の長さは関節角度で変化する.
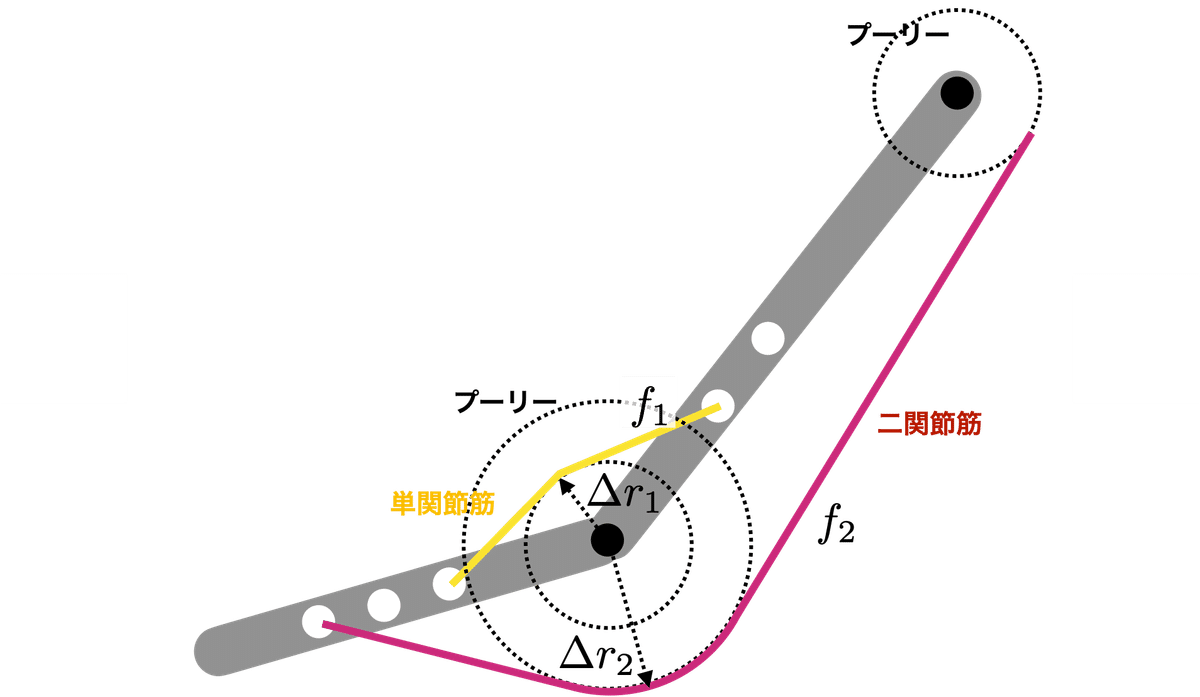
図3では,一つの単関節筋(黄色)と一つの二関節筋(紫色)を示したが,実際の関節では複数の筋群が関節運動に寄与し(黄色と紫の線がもっとたくさんある),$${i}$$番目の筋肉が半径$${\Delta r_i}$$のプーリー機構で接続し,それぞれ筋張力$${f_i}$$が作用していると考える.簡単化のためにプーリー機構を仮定することでのモーメントアームを一定と仮定しているだけで特に意味はない.すると,関節に作用するトルクは
$$
\bm{\tau} = \sum_{i=1}^{n} \Delta r_i ~f_i
$$
で記述でき,単純に図1と似た力–速度特性をもつ筋力特性を加算するだけなので,トルクと角速度でも,図1と似た曲線となることが予想できる.
つまり,図1で想像している筋肉の力–速度曲線の特性は,関節レベルでも似たような特性を持つはずである.
そこで,動力源となる関節のトルクと角速度曲線を描くことで,運動中の関節のインピーダンス変化や状態を知ることができる.
ただし,運動中の角速度とトルクを観察しても,それは最大努力で運動しているとは限らないことは留意されたい.また,安全に最大負荷をかけることも困難で,せいぜいサイベックスなどの等速性収縮と呼ばれる負荷を与えた際の計測に限定されてしまうだろう.
すると最大努力時のトルク–角速度曲線は不明でも,たとえば全力に近い投球時の肩関節の内外旋方向のトルクと角速度を観察することで,筋肉の特性の一部が見えてくるかもしれない.
関節に作用するトルクと角速度特性
第16章
で述べたように,関節をまたいだエネルギーの流れは二種類存在する.
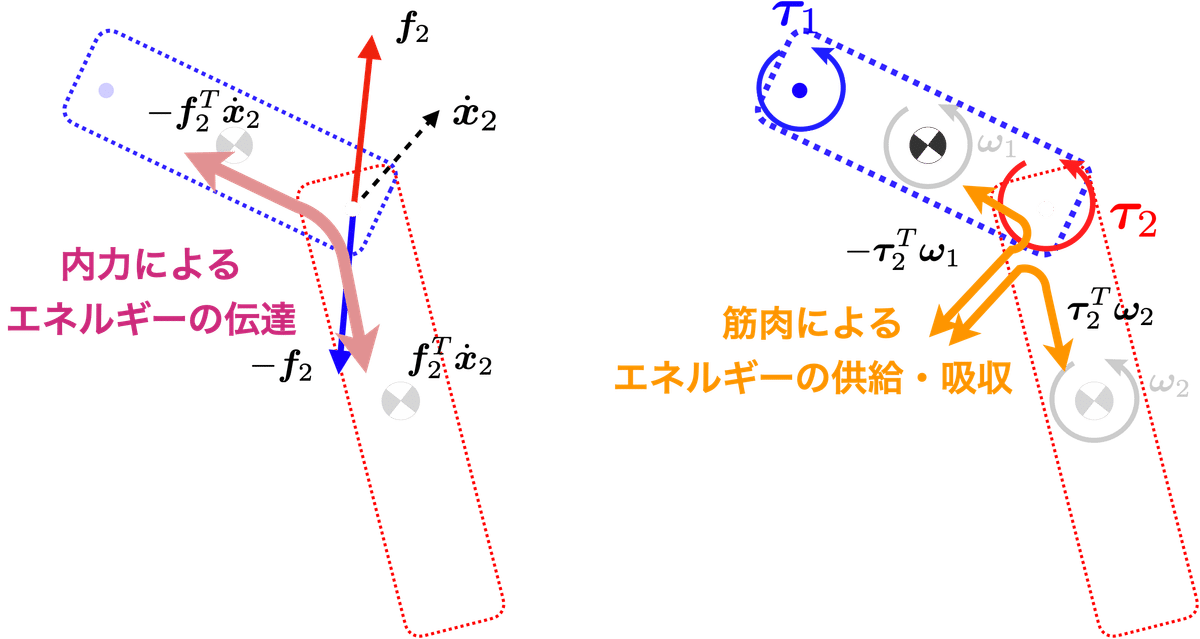
このうち,図4左の関節に作用する力(図4の$${\bm{f}_2}$$)が内力に相当し,これがエネルギーの流れをつくる.関節2で速度$${\dot{\bm{x}}_2}$$を持ち,内力が作用すればエネルギーは関節をまたいで流れ,この流れは$${\bm{f}_2^T \dot{\bm{x}}_2}$$で記述される.
一方,図4右の関節に作用するトルク$${\bm{\tau}_2}$$は,エネルギーを関節をまたぐ2つの部位に,それぞれエネルギーを供給したり,部位からエネルギーを吸収し,その流れは$${-\bm{\tau}_2^T \bm{\omega}_1, \bm{\tau}_2^T \bm{\omega}_2}$$で記述される.
ここで注目すべきは,後者の複数の筋力によって生成される関節のトルクと角速度の関係である.これまでも述べてきたように,動力源からのエネルギーの流れを向上させるために,手先や足先のインピーダンスと整合したい対象は筋肉や関節レベルのインピーダンスである.
そこで,関節トルクによるエネルギー供給・吸収を考えると,2種類のトルク–角速度カーブが描けそうだが,関節のインピーダンスを考えるときには,トルク$${\bm{\tau}_2}$$と相対角速度$${ \bm{\omega}_2 - \bm{\omega}_1}$$の関係を考えるべきである.
なぜなら,$${-\bm{\tau}_2^T \bm{\omega}_1}$$は赤色の部位を固定した際のトルクによるエネルギーの流れを意味し,同様に$${\bm{\tau}_2^T \bm{\omega}_2}$$は青色の部位を固定した際のトルクによるエネルギーの流れを意味し,これらは関節のインピーダンスを考える上で,適切ではない.
これに対して相対角速度$${ \bm{\omega}_2 - \bm{\omega}_1}$$は,トルク$${\bm{\tau}_2}$$によって発生する関節の回転運動を反映しているので,相対角速度$${ \bm{\omega}_2 - \bm{\omega}_1}$$と,トルク$${\bm{\tau}_2}$$との関係を観察することで,関節のインピーダンスを観察することができる.
トルクと角速度の座標変換
ここでは,投球の例における,右利きの投手の右肩関節に作用するトルクと相対角速度との関係を調べる.すると,調べたいトルクと角速度は,右肩(部位$${4}$$)に作用するトルク$${\bm{\tau}_4}$$と,上胴(体幹上部$${2}$$)と右肩間の相対角速度$${\bm{\omega}_4 - \bm{\omega}_2}$$間の関係である.
ただし,これまで示してきたコードにおける,クラスBodyLinkの角速度ベクトル b_link2[4].w は,それぞれの部位に固定されたローカル座標系で記述している.(投球の例における)右肩の角速度は
b_link2[4].wであるが,これは第14章
でも述べているように,右肩に固定された座標系で記述されている.
一方,右肩に作用するトルク
b_link2[4].tau_globalは,絶対座標系で記述されたトルクである.
そこで,これから行う計算では,何らかの座標系で統一して行う必要があるが,ここで,右肩に固定された座標系で計算するのが良いだろう.右肩に固定された座標系では,z軸が上腕の長軸まわりの内外旋軸に相当するためである.
ここで,ベクトルの左上の添字を,そのベクトルを記述する座標系とすると,右肩と体幹上部の角速度 b_link2[4].w, b_link2[2] は
$$
{}^4 \bm{\omega}_4, {}^2 \bm{\omega}_2
$$
に相当する.そこで肩の相対角速度
$$
{}^4 \bm{\omega}_4 - {}^4 \bm{\omega}_2
$$
を計算するためには,一度,体幹上部の角速度$${{}^2 \bm{\omega}_2}$$を絶対座標系の$${{}^g \bm{\omega}_2}$$に変換し,それをさらに右肩の座標系に変換するのが良い.
なぜなら,ここで使用しているコードでは,以下の各部位のローカル座標系と絶対座標系間の座標変換の関数が準備されている.たとえば,絶対座標系からローカル座標系へのベクトルの座標変換と,ローカル座標系から絶対座標系への変換は
frame_to_local(rot_vec, vec)
frame_to_global(rot_vec, vec)の関数で行うことができる.これは,
$$
\bm{R} \bm{a}
$$
に相当し,$${\bm{R}}$$は回転行列,$${\bm{a}}$$はベクトルを意味し,それぞれコードにおける引数 rot_vecとvecに相当する.より具体的に述べると,ローカル座標系で記述された体幹上部の角速度ベクトル$${{}^2 \bm{\omega}_2}$$を絶対座標系に変換するためには,
w_2_global = frame_to_global(b_link2[2].rot, b_link2[2].w)とすればよい.これは$${{}^g\bm{R}_2 {}^2 \bm{\omega}_2}$$に相当する.ここで,$${{}^g\bm{R}_2}$$は体幹上部の座標系から絶対座標系に変換する座標変換行列である.さらに,これを
w_2_local4 = frame_to_local(b_link2[4].rot, w_2_global)とすることで,$${{}^4\bm{R}_g {}^g\bm{R}_2 {}^2 \bm{\omega}_2}$$のように,体幹上部の角速度$${ {}^2 \bm{\omega}_2}$$を,右肩の座標の角速度$${ {}^4 \bm{\omega}_2}$$に変換することができる.
これを利用して相対角速度$${{}^4\bm{\omega}_4 - {}^4\bm{\omega}_2 = {}^4\bm{\omega}_4 - {}^4\bm{R}_g {}^g\bm{R}_2 {}^2 \bm{\omega}_2}$$を
b_link2[4].w - w_2_local4として計算できる.
同様に絶対座標系で記述された右肩の関節トルク$${{}^g \bm{\tau}_4}$$は,
frame_to_local(b_link2[4].rot, b_link2[4].tau_global)で計算を行うことで,体幹上部の座標系のトルク$${{}^4\bm{\tau}_4 = {}^4 \bm{R}_g ~{}^g\bm{\tau}_4}$$に変換すれば良い.
下記に示したコードでは,少し異なるアプローチによる座標変換方法も示しているので,それほど大げさな内容でもないが,座標変換の理解のために参考してしていただきたい.
確認した動作環境とコードについて
いつものように,以下のGoogle ColaboratoryのリンクからブラウザでPythonコードを実行できる.なお,ログインするためには,Googleアカウントが必要となるので注意をされたい.
また,使用するの投球動作のモーションキャプチャのサンプルデータは(sample_optitrack_sec15.csv)は,このリンクからダウンロードして,Google Driveをマウントし,マウントしたドライブにそれらをコピーしてご使用いただきたい.すでにダウンロ度済みの方は,再度ダウンロードする必要はない.
また,Google ColaboratoryやGoogle Driveの使用方法は,
を参照されたい.
なお,ここでのコードは,JupyterLab(デスクトップアプリ),Google Colaboratoryで検証したが,とくにグラフィックスの表示結果やコードは,その二つでも若干動作が異なる.動作させるPython環境に依存し,少々修正が必要となるかも知れない.とりあえずJuputerLabのアプリやGoogle Colabratoryで確認したが,環境によってグラフィックスのコードの調整をお願いしたい.ここで示したコードは,JupyterLabで動作するが,Colabでは若干修正している.
なお,環境によっては,
ax.set_aspect('equal')によって,xyz軸間のスケール比(アスペクト比)を調整し,軸間の長さのスケールを等しくすることができるが,Colabではこれが機能しないため,描画範囲をax.set_xlim(), ax.set_ylim(), ax.set_zlim()で指定している.適宜環境に合わせて調整をしていただきたい.
トルクと角速度による関節のインピーダンスの可視化
ここでは,投球時の肩関節の内外旋軸まわりのトルクと角速度に注目する.この軸まわりのトルクが腕の加速に寄与していることは,確認され,経験的にも内旋トルクが他の軸よりも重要であることは明らかであろう.ただし,肩関節の内外旋軸まわりのトルクと球速が必ずしも比例しないということだけは,補足しておく.これは,肩関節に作用する力によって発生するエネルギーの流れも,大きく寄与するためである.
これまでの章で示してきたように,「パッケージの読み込み」,「ファイルパスの設定」,「クラスの定義」,様々な「関数定義」,「データの格納」を済ませたあとに,以下のニュートン・オイラー法の関節に作用する力とトルクの計算を行い,
b_link2[1].ID_Newton(86., True);
b_link2[1].ID_Euler(True);右肩のトルク$${\bm{\tau}_4}$$を右肩の座標系に変換した$${{}^4\bm{\tau}_4 = {}^4 \bm{R}_g ~{}^g\bm{\tau}_4}$$を以下のコードで示すと,
e_t = 257
t_list = np.arange(e_t+1)/360.
plt.plot(t_list, frame_to_local(b_link2[4].rot, b_link2[4].tau_global)[:e_t+1])
plt.axhline(y=0, linestyle='--', c='k')
plt.xlabel('Time [s]')
plt.ylabel('Torque [Nm]')
plt.legend(['x: ext-flex', 'y: ab-ad', 'z: in-out rotation'])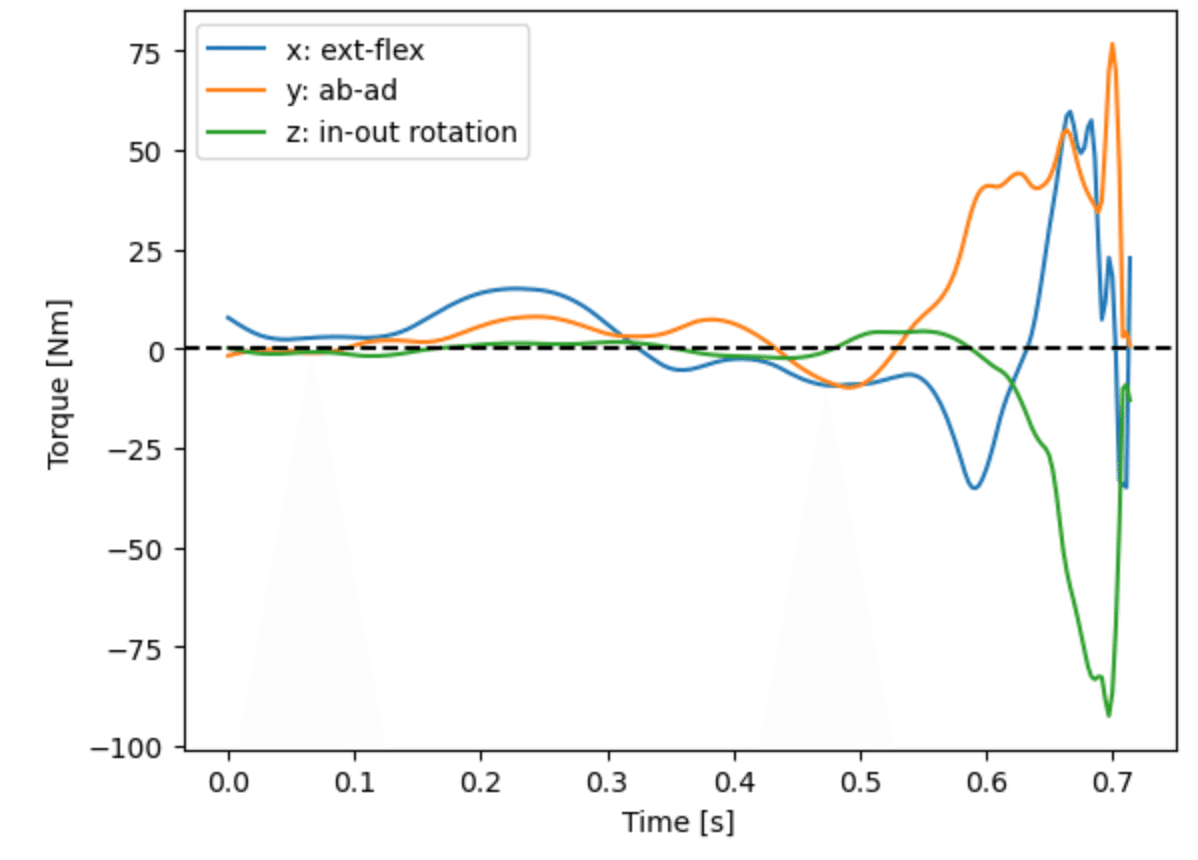
図5のようになる.ここで,xyz軸は以下の図6のように定義され,x, y軸まわりの回転を解剖学的に表現することは,上腕の姿勢に依存するので困難だが(補足1),z軸まわりの回転は内外旋軸に相当する.
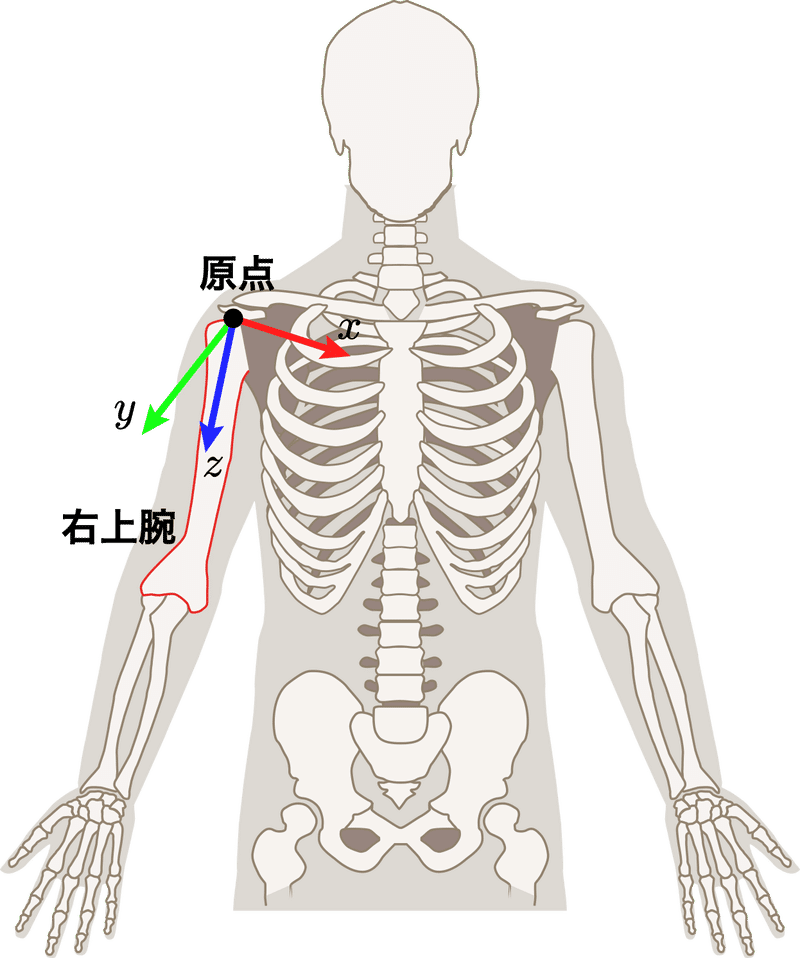
右肩のローカル座標系で示した角速度$${{}^4 \bm{\omega}_4}$$は
t_list = np.arange(e_t+1)/360.
plt.plot(t_list, b_link2[4].w[:e_t+1])
plt.axhline(y=0, linestyle='--', c='k')
plt.xlabel('Time [s]')
plt.ylabel('Angular Velocity [rad/s]')
plt.legend(['x: ext-flex', 'y: ab-ad', 'z: in-out rotation'])図7に示した.
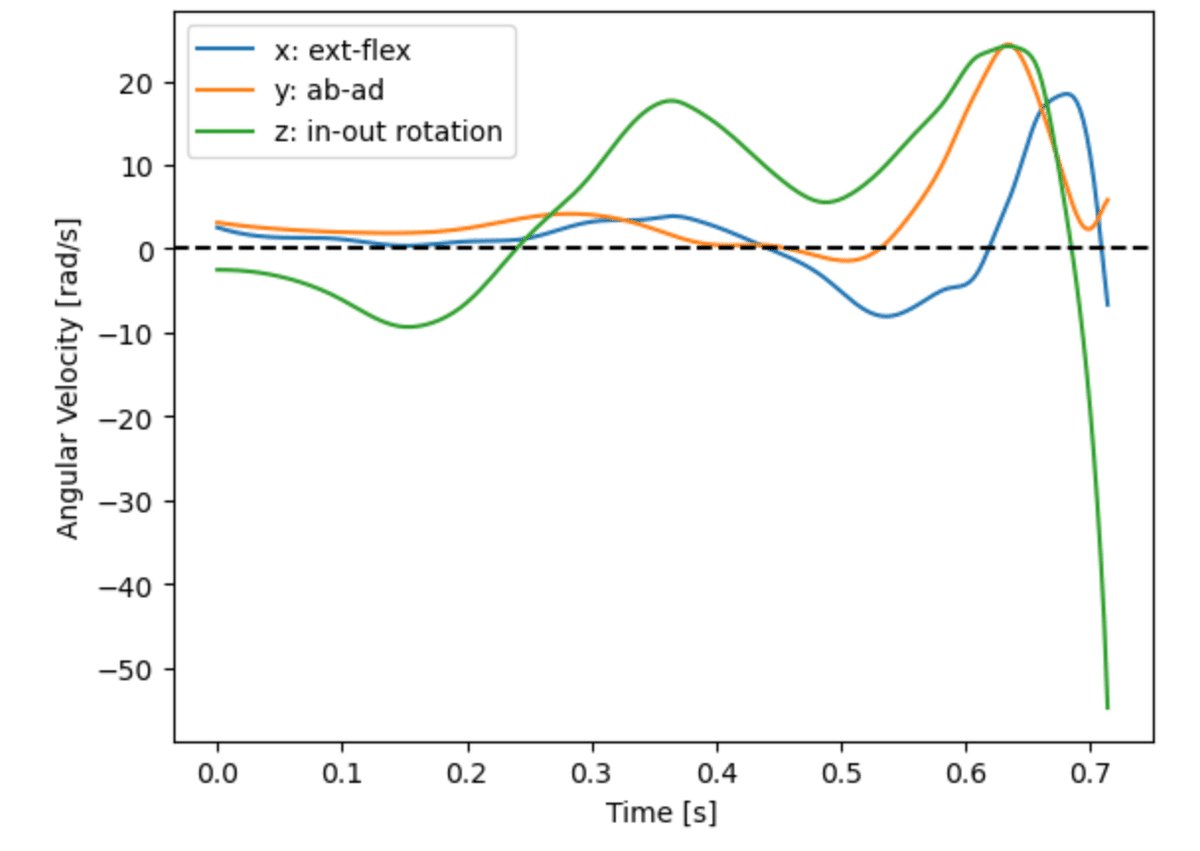
絶対座標系で,上胴2(体幹上部)からみた右上腕4の相対角速度$${{}^{g} \bm{\omega}_4 - {}^g \bm{\omega}_2}$$
relative_w_global = frame_to_global(b_link2[4].rot, b_link2[4].w) - frame_to_global(b_link2[2].rot, b_link2[2].w)は,さらに$${{}^4 \bm{R}_g ({}^{g}\bm{\omega}_4 - {}^g \bm{\omega}_2)}$$の計算によって,
relative_w_local = frame_to_local(b_link2[4].rot, relative_w_global)右肩のローカル座標系に変換し,
t_list = np.arange(e_t+1)/360.
plt.plot(t_list, relative_w_local[:e_t+1])
plt.axhline(y=0, linestyle='--', c='k')
plt.xlabel('Time [s]')
plt.ylabel('Angular Velocity [rad/s]')
plt.legend(['x: ext-flex', 'y: ab-ad', 'z: in-out rotation'])図8に示した.
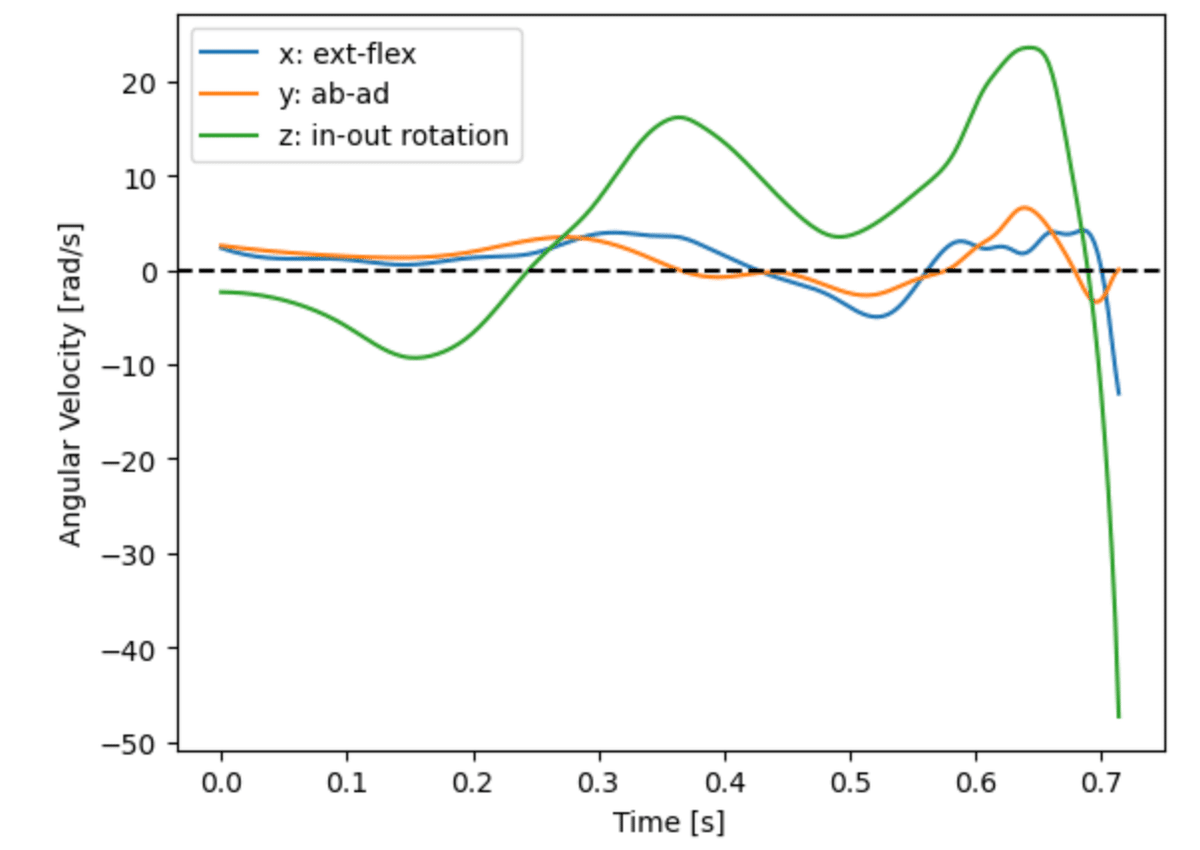
以上で準備が整い,右肩のローカル座標系での相対角速度($${ {}^{4}\bm{\omega}_4 - {}^{4} \bm{\omega}_2 }$$)と右肩のトルク($${{}^{4} \bm{\tau}_4}$$)との関係を,横軸に相対角速度,縦軸にトルクで以下のコードで描くと,
e_t = 257
t_time = 238
plt.plot(relative_w_local[:e_t+1, 0], frame_to_local(b_link2[4].rot, b_link2[4].tau_global)[:e_t+1][:, 0])
plt.plot(relative_w_local[:e_t+1, 1], frame_to_local(b_link2[4].rot, b_link2[4].tau_global)[:e_t+1][:, 1])
plt.plot(-relative_w_local[:e_t+1, 2], -frame_to_local(b_link2[4].rot, b_link2[4].tau_global)[:e_t+1][:, 2])
plt.plot(relative_w_local[t_time, 0], frame_to_local(b_link2[4].rot, b_link2[4].tau_global)[t_time, 0], '.', markersize=15, c='C0')
plt.plot(relative_w_local[t_time, 1], frame_to_local(b_link2[4].rot, b_link2[4].tau_global)[t_time, 1], '.', markersize=15, c='C1')
plt.plot(-relative_w_local[t_time, 2], -frame_to_local(b_link2[4].rot, b_link2[4].tau_global)[t_time, 2], '.', markersize=15, c='C2')
plt.axvline(x=0, linestyle='--', c='k')
plt.axhline(y=0, linestyle='--', c='k')
plt.xlabel('Angular Veloity [rad/s]')
plt.ylabel('Torque [Nm]')
plt.legend(['x: ext-flex', 'y: ab-ad', 'z: in-out rotation'])図9のようになる.
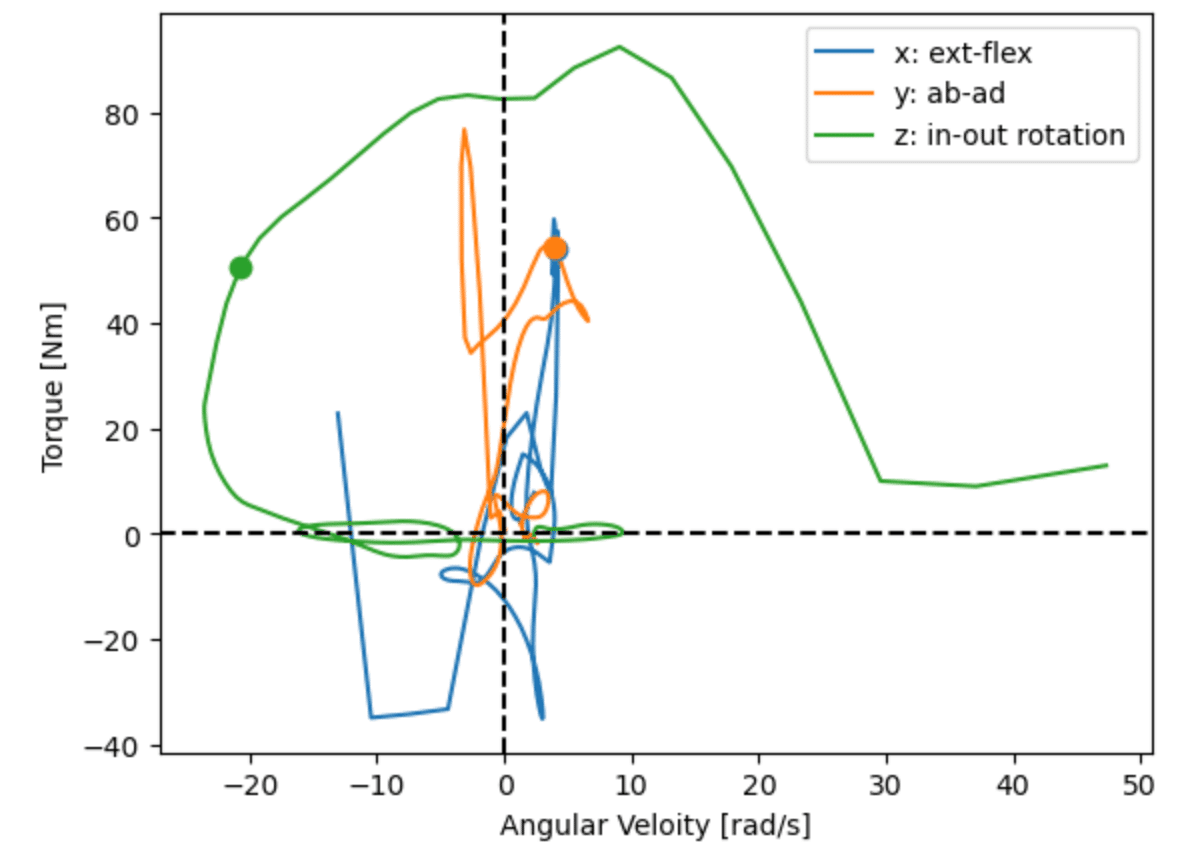
ここで,トルクのうち内外旋のトルク(配列の2列目,緑線)が支配的であることがわかる.そこで以下の解析では,投球時の肩関節の動力源である,内外旋トルクについて注目する.
なお,機械的インピーダンスは,トルクと角速度の比であるので,この比は速度0で無限大となること,またトルクと角速度の両方を示すほうが情報が豊かなので,ここではトルク–角速度曲線のまま示すこととする.
実際の運動では,図1のような曲線を描くわけではなく,また部位ごとでも異なるが,この曲線は競技特性や個人の特性を示しており,トレーニングの目安となるだろう.実際に調べたわけではないが,短距離や跳躍系の選手とスピードスケートの選手の下肢の特性を調べると,大きく異なることだろう.そこで,単に最大挙上負荷を高めたり,収縮速度やパワーを高めるのではなく,「競技で出力される速度(角速度)や姿勢で」高い収縮力(トルク)が発揮する能力が求められる.
トレーニングでは競技特性に見合ったインピーダンスを改善する,いわばインピーダンストレーニングが求められ,姿勢とともに,力と速度をセットに運動の状態を考えることが重要である.
そこで,例えばだが,
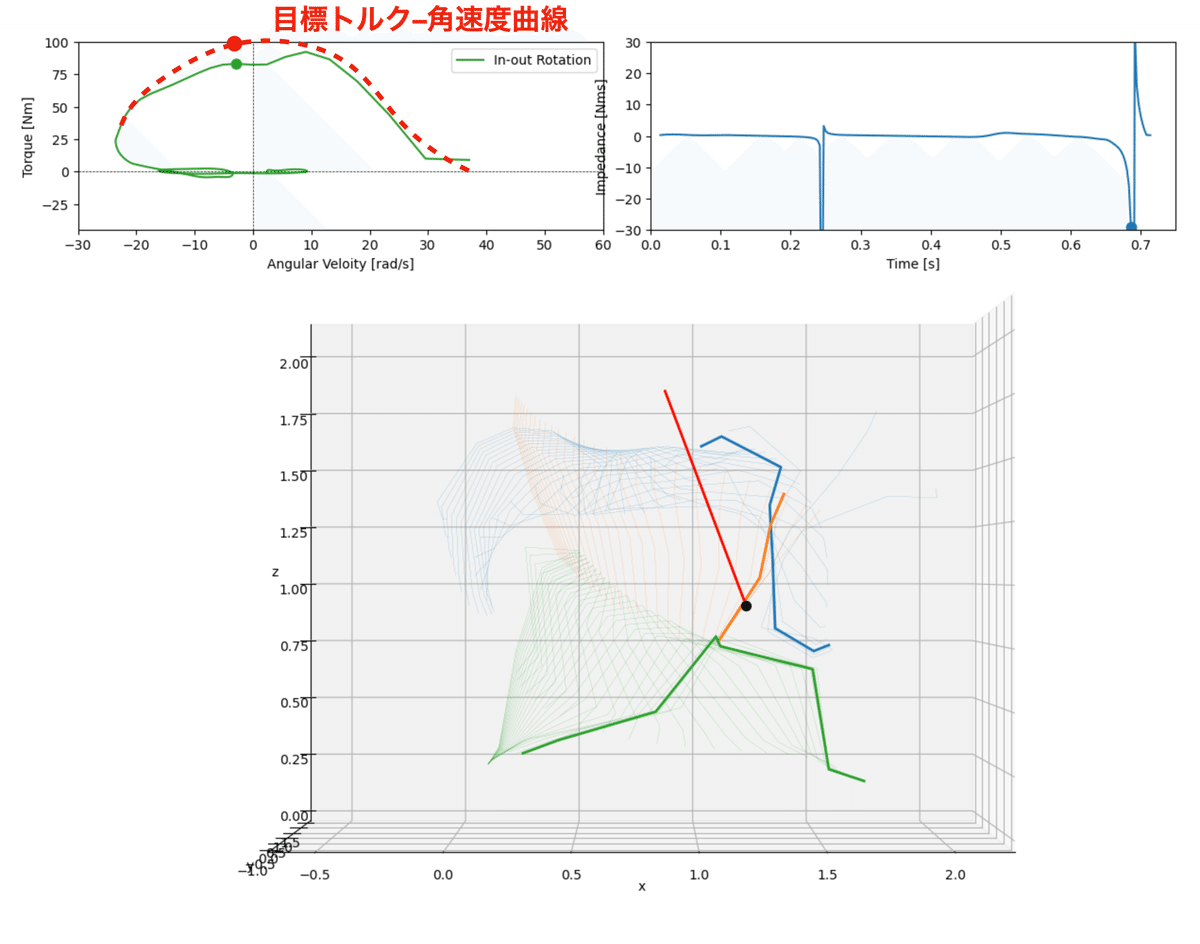
図10に示したように,トルク–角速度曲線において,その競技や個人に見合った目標曲線や目標値を与え,確認しながら改善を行うインピーダンストレーニングを実行することが可能となる.
また,前述したように,ボールの加速し始めはボールに作用する力が大きい割にはボールの速度が小さく,リリース時にはボールに作用する力が弱いが速度は最大近くとなる.つまりボールの機械的インピーダンスを考えると,加速し始めは機械的インピーダンスの高い状態で,リリースに向けて小さく変化していると考えられる.
図9から計算するトルクと相対角速度の比は,正負の符号を示すことになるが,リリースに向けて肘関節が伸展することで,肩と手先間の長さは長くなり,てこ比を変換しながらマッチングが行われていることが予想されるが,ここでは深入りは行わい.
スライダーバーによる動画:右肩関節の内外旋の相対角速度とトルク関係
これまで示した右肩関節トルクと相対角速度の関係を,内外旋軸を中心に検証するが,このときアニメーションで姿勢と比較する.
最初にスライダーバーで,動かしながらアニメーションする方法で示した.これらの可視化の詳細は,第15章
などを参照されたい.
def stick_graph_plot2(body_link):
upper_arm_list = [17, 6, 5, 4, 3, 7, 8, 9, 18] # 腕の関節位置
body_list = [16, 3, 2, 1] # 頭から腰までの関節位置
lower_body_list = [19, 12,11, 10, 13, 14, 15,20] # 下肢の関節位置
x_range=(-.2, 1.75) # x軸描画範囲
y_range=(-.5, 1.) # y軸描画範囲
z_range=(0, 2.1) # z軸描画範囲
step_frame = 10 # アニメーションの際の描画でスキップするフレーム数
q = len(body_link[10].p) // step_frame # フレーム数をstep_sizeで割った,整数の商
max_frame = q * step_frame # 描画する最大フレーム数
# 時間(s)に変換
step_time = .0025 # 2.5 ms毎に描画
sf = 360. # サンプリングレート
q = (len(body_link[10].p) / sf) // step_time # 時間をstep_sizeで割った,整数の商
max_time = q * step_time
cg = b_link2[1].Resultant_Cg(86., True) # 重心位置
cg_acc = smoothing_spline(b_link2[1].Resultant_Cg(86., True), .00005, 360., 2)-[0., 0., -9.8] # 重心位置の加速度+重力加速度
t_list = np.arange(len(b_link2[1].p))/360.
e_t = 257
m = 86. #体重
@interact(time = FloatSlider(min=0, max=max_time, step=step_time, value=0, continuous_update=True), # 描画する時間 [s]
elev = IntSlider(min=-10, max=90, step=5, value=0, continuous_update=True), # ViewPoint(視点)の仰角
azim = IntSlider(min=-180, max=180, step=5, value=-90, continuous_update=True)) # ViewPointの方位角
def plot_3d(elev, azim, time):
fig = plt.figure(figsize=(15, 15))
ax = fig.add_subplot(projection='3d')
ax.view_init(elev=elev, azim=azim)
time2 = int(time * sf)
[stick(ax, body_link, time2, .1, x_range, y_range, z_range) for time2 in range(0, max_frame, step_frame)] # 細い線で重ね描画
stick(ax, body_link, time2, 2, x_range, y_range, z_range) # time2の時間だけを太線でアニメーション
ax.scatter(*cg[time2], s=50, c='k') # 重心
scale = .05
ax.plot([cg[time2, 0], cg[time2, 0]+scale*cg_acc[time2, 0]],
[cg[time2, 1], cg[time2, 1]+scale*cg_acc[time2, 1]],
[cg[time2, 2], cg[time2, 2]+scale*cg_acc[time2, 2]], c='r', linewidth=2) # 重心に作用する力(=床反力の合力)のベクトル
# 角速度 – トルク関係
relative_w4 = b_link2[4].w - frame_to_local(b_link2[4].rot, frame_to_global(b_link2[2].rot, b_link2[2].w)) # 右肩の相対角速度
ax2 = fig.add_subplot(5,4,(1,2))
ax2.plot(-relative_w4[:e_t, 2], -frame_to_local(b_link2[4].rot, b_link2[4].tau_global)[:e_t, 2], c='C2') # 内外旋軸のトルクと相対角速度
ax2.plot(-relative_w4[time2, 2], -frame_to_local(b_link2[4].rot, b_link2[4].tau_global)[time2, 2],'.', markersize=15, c='C2') # time2の時点のトルクと角速度を点で描く
ax2.set_xlim([-30, 60])
ax2.set_ylim([-45, 100])
ax2.axvline(x=0, linestyle='--', c='k', lw = .5)
ax2.axhline(y=0, linestyle='--', c='k', lw = .5)
plt.xlabel('Angular Veloity [rad/s]')
plt.ylabel('Torque [Nm]')
plt.legend(['In-out Rotation'])
# 右肩と手先間の長さ
t_list = np.arange(e_t+1)/360.
ax3 = fig.add_subplot(5,4,(3,4))
len_arm = norm(b_link2[17].p - b_link2[4].p)
ax3.plot(len_arm[:e_t])
ax3.plot(time2, len_arm[time2], '.', markersize=15, c='C0')
ax.plot([b_link2[4].p[time2, 0], b_link2[17].p[time2, 0]],
[b_link2[4].p[time2, 1], b_link2[17].p[time2, 1]],
[b_link2[4].p[time2, 2], b_link2[17].p[time2, 2]], c='b', linewidth = 1, ls='--')
ax3.set_xlim([-10, 270])
ax3.set_ylim([.2, .7])
ax.scatter(*b_link2[4].p[time2], s=30, c='b') # 肩関節
ax.scatter(*b_link2[17].p[time2], s=30, c='b') # 手先
plt.xlabel('Time [s]')
plt.ylabel('Arm length [m]')以上の関数を利用して,描画すると以下のようになる.
stick_graph_plot2(b_link2)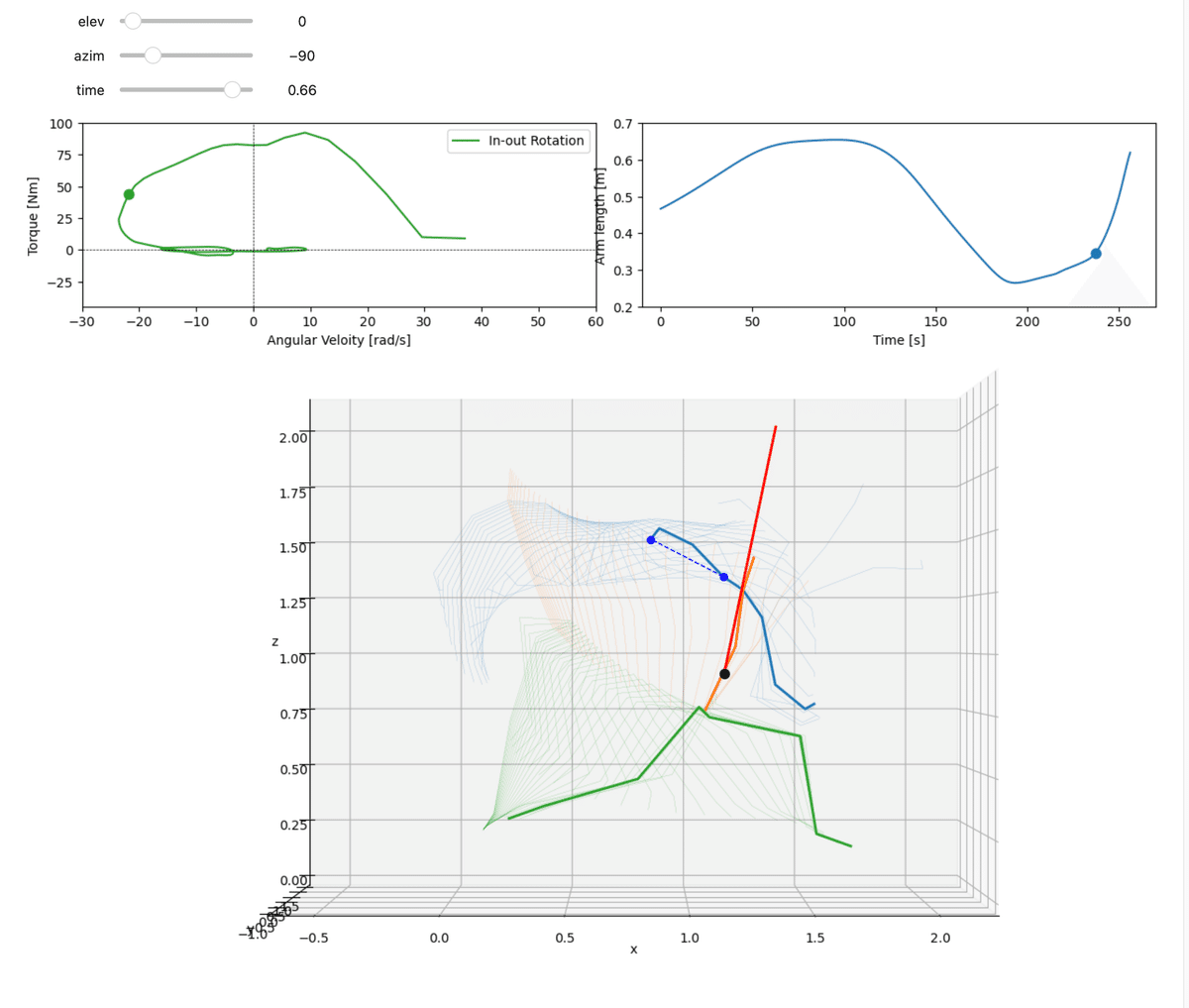
ここで,図11の上の右側には,肩関節(b_link2[4].p)と手先の位置(b_link2[17].p)間の長さを示している.この長さはおおよそ梃子比を表していると,すなわちマッチングトランスファーの目安と考えてよい.
また,スティクピクチャには肩と手先を破線で結び示している.実際にコードを動かして確認をしていただければと思う.
アニメーション:腕に力学的エネルギーの時間変化(仕事率)も可視化
以下の計算に,数分要するので注意されたい.前述の例では,スライダーバーでアニメーションを実行したが,ここでは動画を作成する方法を示した.詳細は同様に,第15章を参照されたい.
この例では,第17章と同様に,エネルギーの流れもスティクピクチャに可視化している.
# アニメーションで使用する重心と,床反力(重心の加速度から計算)
cg = b_link2[1].Resultant_Cg(86., True) # 重心位置
cg_acc = smoothing_spline(b_link2[1].Resultant_Cg(86., True), .00005, 360., 2)-[0., 0., -9.8] # 重心位置の加速度+重力加速度
t_list = np.arange(len(b_link2[1].p))/360.x_range = (-.2, 1.75) # x軸描画範囲
y_range = (-.5, 1.) # y軸描画範囲
z_range = (0., 2.1) # z軸描画範囲
p_elev = 20
p_azim = -110
f_len = 260 # len(b_link2[10].p) # 今回は終わりのフレームを指定した
step_frame = 5 # アニメーションの際の描画でスキップするフレーム数 (5より小さくするとメモリ不足で計算が止まるかもしれない)
q = f_len // step_frame # フレーム数をstep_sizeで割った,整数の商
max_frame = q * step_frame # 描画する最大フレーム数
sf = 360. # サンプリングレート
m = 86. #体重
cg = b_link2[1].Resultant_Cg(86., True) # 重心位置
cg_acc = smoothing_spline(b_link2[1].Resultant_Cg(86., True), .00005, 360., 2)-[0., 0., -9.8] # 重心位置の加速度+重力加速度
# 3Dグラフ領域の作成
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(projection='3d')
ax.view_init(elev=p_elev, azim=p_azim)
ax2 = fig.add_subplot(5,4,(1,2))
ax3 = fig.add_subplot(5,4,(3,4))
e_t = 257
# アニメーション更新用関数の作成
def plot_3d(frame):
ax.cla()
ax2.cla()
ax3.cla()
# 細い線でスティックピクチャを重ね描画
[stick(ax, b_link2, time, .1, x_range, y_range, z_range) for time in range(0, max_frame, 10)]
frame_new = step_frame * frame
stick_power(ax, b_link2, [4, 5, 6], frame_new, \
x_range, y_range, z_range,
lw=2, vec_scale=.5, p_size=15, max_p=7000,
draw_f_power = True, draw_tau_power = True)
# 重心に作用する力(=床反力の合力)のベクトル
ax.scatter(*cg[frame_new], s=50, c='k') # 重心
scale = .05
ax.plot([cg[frame_new, 0], cg[frame_new, 0] + scale * cg_acc[frame_new, 0]],
[cg[frame_new, 1], cg[frame_new, 1] + scale * cg_acc[frame_new, 1]],
[cg[frame_new, 2], cg[frame_new, 2] + scale * cg_acc[frame_new, 2]], c='r', linewidth=2)
# 角速度 – トルク関係
relative_w4 = b_link2[4].w - frame_to_local(b_link2[4].rot, frame_to_global(b_link2[2].rot, b_link2[2].w)) # 右肩の相対角速度
ax2.plot(-relative_w4[:e_t, 2], -frame_to_local(b_link2[4].rot, b_link2[4].tau_global)[:e_t, 2], c='C2') # 内外旋軸
ax2.plot(-relative_w4[frame_new, 2], -frame_to_local(b_link2[4].rot, b_link2[4].tau_global)[frame_new, 2],'.', markersize=15, c='C2') # 内外旋軸
ax2.set_xlim([-30, 60])
ax2.set_ylim([-45, 100])
ax2.axvline(x=0, linestyle='--', c='k', lw = .5)
ax2.axhline(y=0, linestyle='--', c='k', lw = .5)
ax2.set_xlabel('Angular Veloity [rad/s]')
ax2.set_ylabel('Torque [Nm]')
ax2.legend(['In-out Rotation'])
# 右肩と手先間の長さ
t_list = np.arange(e_t+1)/360.
len_arm = norm(b_link2[17].p - b_link2[4].p)
ax3.plot(len_arm[:e_t])
ax3.plot(frame_new, len_arm[frame_new], '.', markersize=15, c='C0')
ax.plot([b_link2[4].p[frame_new, 0], b_link2[17].p[frame_new, 0]],
[b_link2[4].p[frame_new, 1], b_link2[17].p[frame_new, 1]],
[b_link2[4].p[frame_new, 2], b_link2[17].p[frame_new, 2]], c='b', linewidth = 1, ls='--')
ax3.set_xlim([-10, 270])
ax3.set_ylim([.2, .7])
ax.scatter(*b_link2[4].p[frame_new], s=30, c='b') # 肩関節
ax.scatter(*b_link2[17].p[frame_new], s=30, c='b') # 手先
ax3.set_xlabel('Time [s]')
ax3.set_ylabel('Arm length [m]')
# アニメーションのオブジェクトを作成
anim = FuncAnimation(fig, plot_3d, frames = q, interval = 50)
# Jupyter内でアニメーションの表示
plt.close()
HTML(anim.to_jshtml())
### Gif/MP4に保存する場合 ###
#path_dir = '/Users/.../sample_data/'
#path = pathlib.Path(path_dir)
#path_mp4 = path.joinpath('animation_power_impedance.gif')
#anim.save(path_mp4)
#plt.close()
次章について
ここまで,スポーツバイオメカニクスなどで必要とされる,重要な逆動力学を中心とした力学計算についてはおおよそ述べてきた.今後は,それらを補うような力学概念と計算コードについて補足していく.
次章では,全身の角運動量を計算し,その時間微分から地面に発揮される力と力のモーメントを計算し,フォースプレートで計測する情報を身体から推定することを試みる.床反力の推定についてはすでに行っているので,力のモーメントの推定が中心となる.
これが精度良く計算できれば,フォースプレートと同等の情報を得られるので,COP(ZMP)の推定も可能となり,つまりフォースプレートいらずとなるが,果たして結果はどのようになるだろうか.
補足
補足1:解剖学的な用語と身体に固定された座標軸
解剖学的な用語は,多くの場合,数学的,幾何学的に明確に定義をの行いにくく,曖昧な定義が多い.肩関節に限ると,内外転運動とは,どの座標系に固定された回転角度として定義されているか不明瞭であるが,体幹上部に固定された座標形から見た回転運動で定義することができるだろう.
図6で定義された座標系は,上腕に固定された座標系で,解剖学的な用語と整合があるのはz軸の内外旋の回転だけである.



【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
【データの計測について】
スポーツセンシング社のスタジオで,フォースプレートやモーションキャプチャを利用した計測も行えます.出力されるデータと,ここで示したプログラム(入力データの取り込み関数を少々改変する必要があるが)で,同様な解析を行えますので,まずはお気軽にお問い合わせください.
