
動かして学ぶバイオメカニクス#5 〜フィルタリングと加速度計算〜
身体運動における逆動力学計算では,加速度の計算が精度を決定づける.そこで,ここでは,速度・加速度計算ための平滑化と微分について述べる.
平滑化と微分
このシリーズのマガジンでは,モーションキャプチャのデータを利用して逆動力学計算を行うことを想定している.
その際,並進運動の運動方程式,すなわちニュートンの運動方程式の計算では,関節,または解剖学的特徴点を同定するための適切な位置にマーカを貼付し,身体各部位の重心位置などを推定し,その重心の加速度が必要となる.前章ではそれを加速度データとして提供したが,重心の位置ベクトルを数値的に二階微分することで重心の加速度を計算する必要がある.ただし,位置ではあまり気にならない誤差が,微分により誤差が増大し,さらに二階微分では非線形的に増大し,フィルタリングなしに数値微分を行うことは,好条件で計測を行っている場合を除いて多くの場合困難となる.したがって位置ベクトルに対して適切なフィルタリングや数値微分を行う必要がある.
前章では精度的に最も肝心な部分を後回しにし,ニュートンの運動方程式による力の計算を実感することを優先させ,位置からの加速度計算は行わず加速度データとして提供したが,ここでは,その微分とフィルタリングを両立する加速度計算について述べていく.
フィルタリングの古典的な方法として,たとえばバターワース(Butterworth)のローパスフィルタ(lowpass filter)などが一般的に使用されているかもしれないが,これらの周波数ベースの方法は個人的には推奨しない.
理由は簡単である.これらの方法では周波数でノイズと信号を分離するわけだが,「除去すべきノイズの周波数帯にも有効な信号が含まれている」ことがほとんどで,綺麗にノイズをフィルタリングするほど信号も低減してしまう.モーションキャプチャなどで計測する多くの場合は,分離は困難である.ノイズの特性にも依存するが,加速度計やジャイロセンサなどのセンサに対しては,信号の帯域が異なるので周波数ベースのフィルタが有効なときが多いが,光学系の位置計測では周波数ベースのフィルタの使用を避けたほうが懸命である.
実際に加速度センサのデータと,加速度センサのマーカから計算した加速度を比較を行えば,その違いがすぐに分かるが,たとえばバターワースフィルタでノイズを除去すると,本来の加速度の信号までもカットし,滑らかになりすぎていることがわかる.正しい加速度と比較が困難なゆえに,ノイズを低減させることを優先し,本来の信号もカットしてしまっている人は案外多いかもしれない.
また,どのようなフィルタリングを行うにせよ,平滑化した後,数値微分を行うのが通例であるが,前方差分,後方差分,中心差分にせよ誤差が発生する.数値微分の誤差にも無頓着になりががちだが,これらをセットで解決するのがここでの狙いである.
ここで紹介する平滑化スプラインは,多くの場合有効だが,いくつかの注意点もあるので,最後にまとめた.
コードについて
下記に示したコードは,前章同様,以下のGoogle Colaboratoryのリンクから,Pythonをインストールせずに,ブラウザでPythonコードを実行できるようにした.なお,ログインするためには,Googleアカウントが必要となるので注意をされたい.
また,後半で使用するサンプルデータ(sample_220908.csv)は,サンプルデータのリンクからダウンロードして,Google Driveをマウントし,マウントしたドライブにコピーして,ご使用いただきたい.
なお,Google ColaboratoryやGoogle Driveの使用方法は,
を参照されたい.
平滑化スプライン
平滑化スプライン(smoothing spline)は,観測データをスプライン関数(spline function)で近似する.ただし,これは「オリジナルのデータを必ず通る」補間(interpolation)ではないことに注意されたい.スプライン関数による関数近似は行うが,曲線を二階微分しても滑らかになるような4次の関数を選択し,かつオリジナルのデータの「近傍」を通る点に最適化することで,平滑化と微分を同時に実現する.
少し寄り道になるが,平滑化スプラインについて述べる前に,まず多項式補間とスプライン補間について述べておく.
観測データの多項式による関数近似

時系列の観測データ$${(x_1, y_1), \dots, (x_n, y_n)}$$のうち,図1の点のように観測データ$${(x_1, y_1), (x_2, y_2)}$$を関数(曲線)$${f(x)}$$で結ぶことを考える.ただし,$${x_1<\cdots < x_n}$$とする.
たとえば,2点$${(x_1, y_1), (x_2, y_2)}$$を通るように,関数$${f(x)}$$を1次式
$$
f(x) = a x + b
$$
で定める場合,線形補間となる(図1,黒破線).さらに,2次関数
$$
f(x) = a x^2 + b x + c
$$
で近似することも可能だが,2点$${(x_1, y_1), (x_2, y_2)}$$を通るだけでは未知数$${a,b,c}$$を定められないので,例えば,隣の区間との接する点$${(x2, y_2)}$$の傾き(速度)
$$
f'(x) =2 a x + b
$$
を定めることで,2次関数の係数を定め,図1の青色の破線のように描くことができる.
3次関数
$$
f(x) = a x^3 + b x^2 + c x + d
$$
の場合は,2点と,点$${(x_2, y_2)}$$における傾き$${f'(x)=3ax^2+2bx+c}$$と,さらに加速度$${f''(x)=6x+2b}$$を定めることで4つの係数($${a,b,c,d}$$)を定めることができる(図1,赤破線).
これらの傾きは隣の区間の曲線と滑らかに曲線が接続する条件となり,全区間で滑らかに接続される曲線が担保される.これを多項式補間と呼ぶ.

多項式補間はPythonにも実装されており,上記の図は関数interp1d()
を使用し,
from scipy.interpolate import interp1d
import numpy as np
import matplotlib.pyplot as pltx = np.linspace(0, 10, num=11, endpoint=True)
y = np.cos(-x**2/9.0)
f = interp1d(x, y)
f2 = interp1d(x, y, kind='quadratic')
f3 = interp1d(x, y, kind='cubic')xnew = np.linspace(0, 10, num=101, endpoint=True)
plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--', xnew, f3(xnew), '--')
plt.legend(['data', 'linear','quadratic', 'cubic'], loc='best')
plt.show()で描くことができる.これは.Pythonの補間のユーザガイドの例題
を加工しただけである.
このように,特に各区間を低次の多項式で記述し,区間の境界で傾き(微分)が一致するように接続させる補間をスプライン補間(spline interpolation)と呼ぶ.
スプライン補間は,多項式補間としての性質は上記の例と等価で,時系列データを滑らかな曲線で補間する際の代表的な方法である.ただし,以下に述べていくそれ以外の便利な特性があり,Pythonでも別途実装されている.
スプライン補間と微分
スプライン関数は各区間を多項式で記述しているため,多項式関数の導関数を計算できる.ここでは,時系列データを意識して,4次関数を$${f(t) = a t^4 + b t^3 + c t^2 + d t + e}$$と記述すると,その二階微分は$${\frac{d^2f(t)}{dt} = \ddot{f}(t) = 12a t^2+ 6 b t+ 2c}$$となるので,変位$${f(t)}$$と二階微分である加速度$${\ddot{f}(t)}$$間には数学的な厳密な微分関係があるので,数値微分の単なる差分と異なり,関数の微分によって正確な微分を実現し,加速度も2次関数となり滑らかな加速度曲線を得ることができる.
Pythonのスプライン補間はscipy.interpolate.UnivariateSplineのライブラリ
を,下記のように
from scipy.interpolate import UnivariateSpline平滑化スプラインのモジュールをimportsし
f4 = UnivariateSpline(x, y, s=0, k=4)と計算すれば良い.ここで,s=0とすることで,観測データを通る補間を実現し,k=4とすることで4次のスプライン関数(多項式)で補間する.以下のようにグラフを書くと
plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--', xnew, f3(xnew), '--')
plt.plot(xnew,f4(xnew), color='black')
plt.legend(['data', 'linear','quadratic', 'cubic', 'spline'], loc='best')
plt.show()
のように,4次の多項式,すなわちスプライン関数で補間をした結果が得られる.補間の場合,次数が高くなるほど,波形が鋭く変化することがわかる.
スプライン関数の微分は
df4_1 = UnivariateSpline(x, y, s=0, k=4).derivative(n=1)
df4_2 = UnivariateSpline(x, y, s=0, k=4).derivative(n=2)のように.derivative(n=1)を付け加えることで速度(一階導関数)を,.derivative(n=2)を付け加えることで加速度(二階導関数)を計算することができ,
plt.plot(x, y, 'o')
plt.plot(xnew, f4(xnew))
plt.plot(xnew, df4_1(xnew))
plt.plot(xnew, df4_2(xnew))
plt.legend(['data', 'spline','velocity', 'acceleration'], loc='best')
plt.show()
のような変位(spline補間),速度(velocity),加速度(acceleration)のグラフを得ることができる.
平滑化スプライン
スプライン補間は観測データを通過するように関数近似する.しかし,忠実に観測データを通過する補間関数を二階微分すると,比較的精度良く計測されたデータ(図5左)でも,その二階微分はかなり暴れ,

図5右のようになる.
そこで,オリジナルの観測データ近くを通る曲線(関数)で,かつ,その関数$${f(t)}$$が滑らかになるように最適化で決定する方法が平滑化スプライン(smoothing spline)である.「滑らかさ」は曲線の二階微分$${\ddot{f}(t)}$$が暴れないように小さくすることで担保する.
すなわち,平滑化スプラインは,「近似度」+「関数の滑らかさ」の最適化によってスプライン関数を決定する方法である.この「近似度」と「関数の滑らかさ」は,一般には,
観測データ$${(x_1, y_1), \dots, (x_n, y_n)}$$がある時,
$$
J_{\lambda}(f) = \sum_{i=1}^n (y_i - f(x_i))^2 + \lambda \int f''(x)^2 dx
$$
の評価関数を最小化することで実現するする.ここで,$${\lambda>0}$$は平滑化パラメータと呼ばれ,滑らかさを決める重みづけのパラメータである.

$${y_i}$$は時刻$${i}$$のときの計測データを示し,$${f(x_i)}$$が近似関数を表す(図6赤線).
近似度:
第1項の中の$${(y_i - f(x_i))^2}$$は時刻$${i}$$の観測値(オリジナルのデータ)と(求めるべき)近似関数との二乗誤差を表すので,第1項は近似の悪さに対するペナルティである.
関数の滑らかさ:
第2項の$${f''(x)}$$は関数$${f(x)}$$の二階微分で,曲線が複雑になることに対するペナルティを示している.
これらの2つの評価を,平滑化パラメータという重み係数で配分し最小化で決定するのが平滑化スプラインである.
もし$${f(x_i)}$$が4次関数ならひとつひとつのデータの間(図1の点線間)を
$$
f(x) = a x^4 + b x^3 + cx^2 +dx +e
$$
の関数で埋めていく.データの境界では,曲線の傾き(一階微分から三階微分まで)が一致するように接続するので,データ全体でも滑らかさが担保される.
スプライン関数が4次以上の関数であれば,二階部分した加速度も$${f''(x)=12 x^2+6 bx+2c}$$で結ぶので,加速度も2次関数で記述され,全区間で滑らかな加速度が得られる.
なお,場合によっては5次以上を選択することも必要になるかもしれないが,計算量が増えることと,次数が大きくなることで波形が暴れる可能性が増える理由から,加速度を計算する場合は4次が無難だろう.加速度を計算しないなら3次で十分である.
図5で示したように,図6のオレンジ色の二階微分$${f''(x)}$$が暴れるほど,第2項が大きくなるので,$${\lambda}$$が小さいと$${f(x)}$$が蛇行し滑らかさが減る曲線となるが,一方で観測データに近い曲線となる.$${\lambda=0}$$とすると,単なるスプライン関数への補間となり,水色の線を通る曲線に関数近似され,補間を実行することになる.
$${\lambda}$$が反対に大きすぎると,観測データを追随することなく曲線は滑らかになる.
そこで適切な$${\lambda}$$を選択する必要がある.問題はその適切さをどのように決定するかだが,以後示すような,筆者の知識ではデータの近似度,加速度の暴れ具合,加速度センサとの比較ぐらいしか答えられない.
以下では,Pythonの 平滑化スプラインとしてUnivariateSplineを利用するが,Matlabにも実装されているようである.
平滑化スプライン Scipy.UnivariateSpline()の基本
以下に,Pythonの平滑化スプラインの関数の仕様と使用方法についてまとめる.
ここで,モーションキャプチャのデータ処理を意識し,時間軸と観測データを下記のように,timeとyとして与える.
# 時間軸(x軸)
time = [0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. ] # = np.arange(0, 2*np.pi, .5)
# 時系列観測データ
# np.sin(time)+np.random.randn(len(y))/20.
# 三角関数+乱数
y = np.array([ 0.01060855, 0.49403123, 0.7794513 , 0.98637471, 0.96506601,
0.65524765, 0.24423349, -0.4020829 , -0.86418404, -1.04206452,
-0.97197121, -0.78730514, -0.28842717])sオプション:平滑化パラメータλ の選択:
平滑化パラメータλは, Scipy.UnivariateSpline()では,sオプションで与える.s = 0とすると,スプライン補間と等価になる(ただしs=0の場合,次で述べる Nan には対応できないので,その場合は,単にデータからNanを含むデータを除去すること).sは正の値を選択すること.
# 以下の2種類のλ(平滑パラメータ,sオプション)で検証
spl1 = UnivariateSpline(time, y, s=0.0001)
spl2 = UnivariateSpline(time, y, s=0.2)とすることで,スプライン関数spl1やspl2を定義できる.これは関数spl1(), spl2()のように「関数」と考え,この関数に任意の時間軸を配列で与えれば,補間と同様にデータを得ることができる.
たとえば,さらに時間間隔を2分の1にし,
time2 = np.arange(0, 2*np.pi-.1, .25)と時間軸を定義し,これを先程の関数の変数としてtime1とtime2をとり,spl1(time2), spl2(time2)与えることで,「数値」を得ることができる.そこで,以下では2種類の平滑化パラメータ$${\lambda}$$をsオプションで与える(s=0.00001, s=0.2).
plt.plot(time, y, '.', markersize=15, c='orange') # 時系列観測データy(三角関数+乱数)
plt.plot(time2, spl1(time2), '.', markersize=5, c='C0') # s=0.0001で平滑化した補間データ
plt.plot(time2, spl1(time2), lw = .5, c='C0') # spl1() 補間関数カーブ
plt.plot(time2, spl2(time2), '.', markersize=5, c='C1') # s=0.2で平滑化した補間データ
plt.plot(time2, spl2(time2), lw = .5, c='C1') # spl2() 補間関数カーブ
plt.legend(['y: data', 'spl1 ($\u03bb$=0.0001)', 'spl1(time)', 'spl2 ($\u03bb$=0.2)', 'spl2(time)'])
λが小さいと,より観測データに近く関数近似し(青),λが大きいと,より滑らかに関数近似を行う(オレンジ).
ここで,平滑化パラメータ($${s=0}$$)とすると,単なるスプライン補間となる.
sの値は,データの数,暴れ具合で適切な値の選択がかわる.xyz軸が同じ暴れ具合であれば,共通のsを選択してもよいが,たとえばz軸だけノイズが多いときは,個別に選択するべきであろう.データの単位によっても異なる.モーションキャプチャでmを単位としているときは,データの長さに依存するが,例えばだが,かなり小さい0.0000001から,1の間ぐらいで選択することが多い.基準がないに等しいので,選択の際ののあくまでも参考として捉えていただき,ご自身で適切さを決定していただきたい.
Scipy.UnivariateSpline()の,s オプション:平滑化パラメータ(s>0)
wオプション:欠損データ(Nan)への対応
以下のように,観測データのyに2箇所欠損データを含むように,yを修正
# yを欠損データを含むデータに修正
y34 = np.array([ 0.01060855, 0.49403123, np.nan , 0.98637471, 0.96506601,
0.65524765, 0.24423349, -0.4020829 , np.nan, -1.04206452,
-0.97197121, -0.78730514, -0.28842717])
# 配列の要素に欠損データがある要素はTrueを返して,配列w34に格納
w34 = np.isnan(y34)
print(w34)
>>> [False False True False False False False False True False False False
False]"~" はビット反転でTure(1)とFalse(0)を反転させる.
print(~w34)
>>> array([ True, True, False, True, True, True, True, True, False,
True, True, True, True])欠損値にNanを含む場合,関数近似を行えない.そこで,単に時間軸time とデータy34から,Nanを含む要素を除去してもよいが,wオプションで,配列~w34を与えることで,Nanのデータを計算に使用しない(除去したことと等価になる)ことが可能となる.
Scipy.UnivariateSpline()の,w オプション:正の値で,各要素(配列で与える)にさらに重みを与えられる.ここでは,下記のようにwのオプションの値を与える.
False=0(無視:除去と等価),True=1(計算に使用する)
なお,データがNanのままでは計算ができないので,なんでもよいのでNanを一旦数値に変換する.ここでは,下記のように0として代入する.無視するだけなので,この値は計算に影響しない.
# 要素がNanでは計算ができない,そこで,
# wの要素がTrue(Nan)の要素の場合,データy34を0に置き換える
# この値はなんでもよい.なぜならwオプションでFalseのデータは無視するため
y34[w34] = 0.
print(y34)
>>> [ 0.01060855 0.49403123 0. 0.98637471 0.96506601 0.65524765
0.24423349 -0.4020829 0. -1.04206452 -0.97197121 -0.78730514
-0.28842717]さらに以下のように,wオプションを使用することでNanを無視し,2種類の平滑化パラメータで欠損データを含む観測値y34を平滑化スプランで計算し,
spl3 = UnivariateSpline(time, y34, w=~w34, s=.00001)
spl4 = UnivariateSpline(time, y34, w=~w34, s=.2)
Nanを無視していることが確認できた.
kオプション:多項式の次数(デフォルト:3次)
補間に使用する多項式の次数が大きいと,より複雑な波形で関数近似できるが,データとデータを結ぶ曲線は次数が高くなると,暴れやすいという弊害も大きい.
補間目的では一般には3次のスプライン関数が用いられるが,それでは3次多項式の二階微分は1次式,すなわち直線補間になってしまうので,ここでは k=4 として,4次の関数を選択する.こうすることで,加速度も滑らかな曲線(2次式)でデータを関数近似できる.
# 平滑化パラメータλ = 0.00001 の場合
spl3_3 = UnivariateSpline(time, y34, w=~w34, s=.00001)
spl3_4 = UnivariateSpline(time, y34, w=~w34, s=.00001, k = 4)のように2種類の次数で比較しながら,平滑化スプライン関数を計算した.
plt.plot(time, y34, '.', markersize=15, c='orange') # 時系列観測データy(三角関数+乱数)
plt.plot(time2, spl3_3(time2), c='C0')
plt.plot(time2, spl3_4(time2), c='C2')
plt.legend(['y: data with nan', 'k=3', 'k=4'])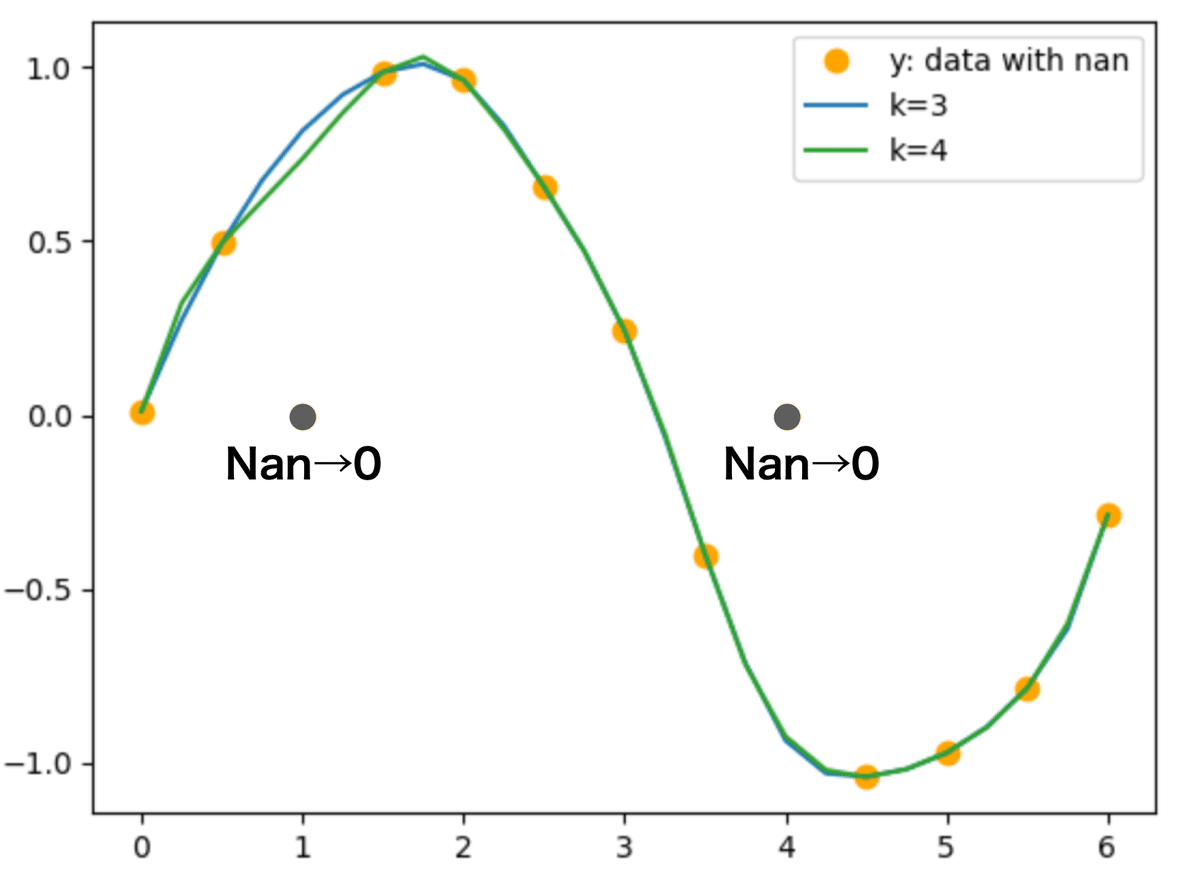
次数が4のほうが特にNan近辺で滑らかに補間してくれているが,次数が高いほどよいというわけではないので注意されたい.
Scipy.UnivariateSpline()の,k オプション:スプライン関数の多項式の次数を選択.
k = 3:デフォルト.
k = 4 :加速度を計算することを考えた場合は,k=4を選択すること.
derivatives(nオプション) による微分値の取得
UnivariateSpline()は取得したスプライン関数の導関数(微分)も計算でき,速度や加速度も取得することが可能である.
のように.derivative(n=1)を付け加えることで速度(一階導関数)を,.derivative(n=2)を付け加えることで加速度(二階導関数)を計算することができ,
たとえば,速度は
# 導関数
# 一階微分(速度)
d_spl4_4 = UnivariateSpline(time, y34, w=~w34, s=.2, k=4).derivative(n=1)
print(d_spl4_4(time))
>>> [ 1.58214347 0.96879867 0.4160607 -0.06019969 -0.44411173 -0.71980465
-0.87140768 -0.88305006 -0.73886102 -0.42296981 0.08049436 0.78740224
1.7136246 ]のように.derivative(n=1)を付け加えることで,スプライン関数の速度(一階導関数:d_spl4_4)と微分値(d_spl4_4(time))を,
# 二階微分(加速度)
dd_spl4_4 = UnivariateSpline(time, y34, w=~w34, s=.2, k=4).derivative(n=2)
print(dd_spl4_4(time))
>>> [-1.27671591 -1.17137303 -1.03428862 -0.86546268 -0.66489521 -0.4325862
-0.16853567 0.1272564 0.45479 0.81406513 1.20508179 1.62783998
2.08233971]のうに.derivative(n=2)を付け加えることで,スプライン関数の加速度(二階導関数:dd_spl4_4)と微分値(dd_spl4_4(time))を計算できる.
なお,.derivative(n=0)は,微分を行わないことを意味する.
そこで,以下のように,
plt.plot(time, y34, '.', markersize=15, c='orange') # 時系列観測データy(三角関数+乱数)
plt.plot(time2, spl4_4(time2)) # 時系列観測データy(三角関数+乱数+Nan)
plt.plot(time2, d_spl4_4(time2)) # 速度
plt.plot(time2, dd_spl4_4(time2)) # 加速度
plt.legend(['y: data with Nan', 'smoothing spline (k=4, s=.2)', 'velocity', 'acceleration'])
例題の速度と加速度を計算してみた(図10).
まとめ
UnivariateSpline(time, y, w, s, k)のオプション
w: 欠損値Nanの対応
s:平滑化パラメータ
k:補間多項式の次数
導関数(微分)のオプション
UnivariateSpline(time, y, w, s, k).derivative(n)
n:微分の階数
Pythonにおける平滑化スプライン
ここで前回同様,Pandasと Numpyのモジュールをimportし,さらにサンプルデータ(sample_220908.csv)を左のリンクからダウンロードしていただき,前回同様,ファイルのパスをご自身の計算環境にあわせて下記を参考に指定し,
import pandas as pd
import numpy as np
from scipy.interpolate import UnivariateSpline
file_path_5 = '/Users/…../sample_220908.csv' # Mac環境の例
file_path_5 = 'C:\Users\...\sample_220908.csv' # Windows環境の例第3章
と同様に,下記の関節データを抽出する関数を定義する.
# CSVデータからヘッダだけ抽出
def extract_df_header(file_path):
return pd.read_csv(file_path, header=None, nrows=5, index_col=1).T
# skeletonの名前を抽出
def extract_skeleton_name(file_path):
df = extract_df_header(file_path)
marker_name = df['Name'][2]
position_col = marker_name.find(':')
return marker_name[:position_col]
# ファイル名とマーカの名前を引数に与えてデータを抽出する関数
def extract_marker(file_path, marker_name):
sk_name = extract_skeleton_name(file_path) # skeleton
df_main = pd.read_csv(file_path, header=[4]) # データだけ抽出
df = extract_df_header(file_path) # headerだけ抽出
df_selected = df[df['Name'] == sk_name+':'+marker_name] # ヘッダがName_Nameと一致する部分だけ抽出
selected_rows = df_selected.index # 一致する列
marker_data = np.array(df_main.iloc[:, selected_rows[-3:]].values) # 後ろから3個データを取得す
return marker_dataベクトルに対応した平滑化スプライン関数の定義:
また,前節で説明したScipy.UnivariateSpline()を使用して,xyzの3次の位置ベクトルの計算に対応し,関数を以下のsmoothing_spline()
# 微分と平滑化を同時にスプライン平滑化で行う
# order=0:変位(微分を行わない),order=1:速度, order=2:加速度
def smoothing_spline(vec_data, weight, sf, order=0, degree=4):
vec_copy = copy.copy(vec_data)
vec_data_t = vec_copy.T
len_num = len(vec_data)
len_vec = len(vec_data_t)
time = np.arange(0, len_num)/sf
w_a = [np.isnan(x) for x in vec_data_t]
spl = [0]*len_vec
for i in range(len_vec):
vec_data_t[i][w_a[i]] = 0.
w_a[i] = ~w_a[i]
spl[i] = UnivariateSpline(time, vec_data_t[i], w_a[i], s=weight, k=degree).derivative(n=order)(time)
return np.array(spl).Tも定義する.
さて, extract_marker()を利用して右手関節の位置ベクトルのグラフを
y = extract_marker(file_path_5, 'RHand')
sf = 360. # sampling frequency
time = np.arange(0, len(y))/sf
plt.plot(time, y)
plt.xlabel('Time [s]')
plt.ylabel('Position [m]')
plt.legend(['x', 'y', 'z'], loc='best')で描くと,

のようになる.
そこで,図11のデータをスプライン補間を利用し,先程のように微分する.
ここで,右手首の位置ベクトルの位置を,4次のスプライン補間を行い,その関数を二階微分することで加速度を計算(s=0:平滑化は行っていない)している.
plt.plot(time, np.array([UnivariateSpline(time, y[:, i], s=0, k=4).derivative(n=2)(time) for i in range(3)]).T)
plt.xlabel('Time [s]')
plt.ylabel('Acceration[m/s2]')
plt.legend(['x', 'y', 'z'], loc='best')
図12のように加速度は暴れていてノイズに埋まってしまう.そこで平滑化スプラインを適用する.
このデータに対して,平滑化スプラインを適用する.
# 以下は
# w = np.isnan(y[:, 0]) # Nanの処理
# np.array([UnivariateSpline(time, y[:, i], w=~w, s=.00001, k=4).derivative(n=2)(time) for i in range(3)]).Tと等価
# y(RHandの位置ベクトル)の加速度ベクトル
plt.plot(time, smoothing_spline(y, .00001, 360., order=2))
plt.xlabel('Time [s]')
plt.ylabel('Acceration[m/s2]')
plt.legend(['x', 'y', 'z'], loc='best')と計算することで(ここで$${\lambda=.00001}$$),

のような加速度を得る.
ここで観測データ(x成分)と,平滑化スプライン後の位置データとの差分を可視化するため,最初に描画した右手首の位置ベクトルについて,下記のように描画する.ここで,
実線:観測データ
破線:スプライン平滑化(観測データとほぼ一致するので,-0.02を加算)
を下記のように比較すると
plt.plot(time, y)
[plt.plot(time, smoothing_spline(y, .00001, 360., order=0)[:,n]-.02, \
ls='--', c=['C0', 'C1', 'C2'][n]) for n in range(3)]
plt.ylabel('Position[m]')
plt.legend(['measurement:x', 'measurement:y', 'measurement:z', \
'spline:x', 'spline:z', 'spline:z'], loc='best')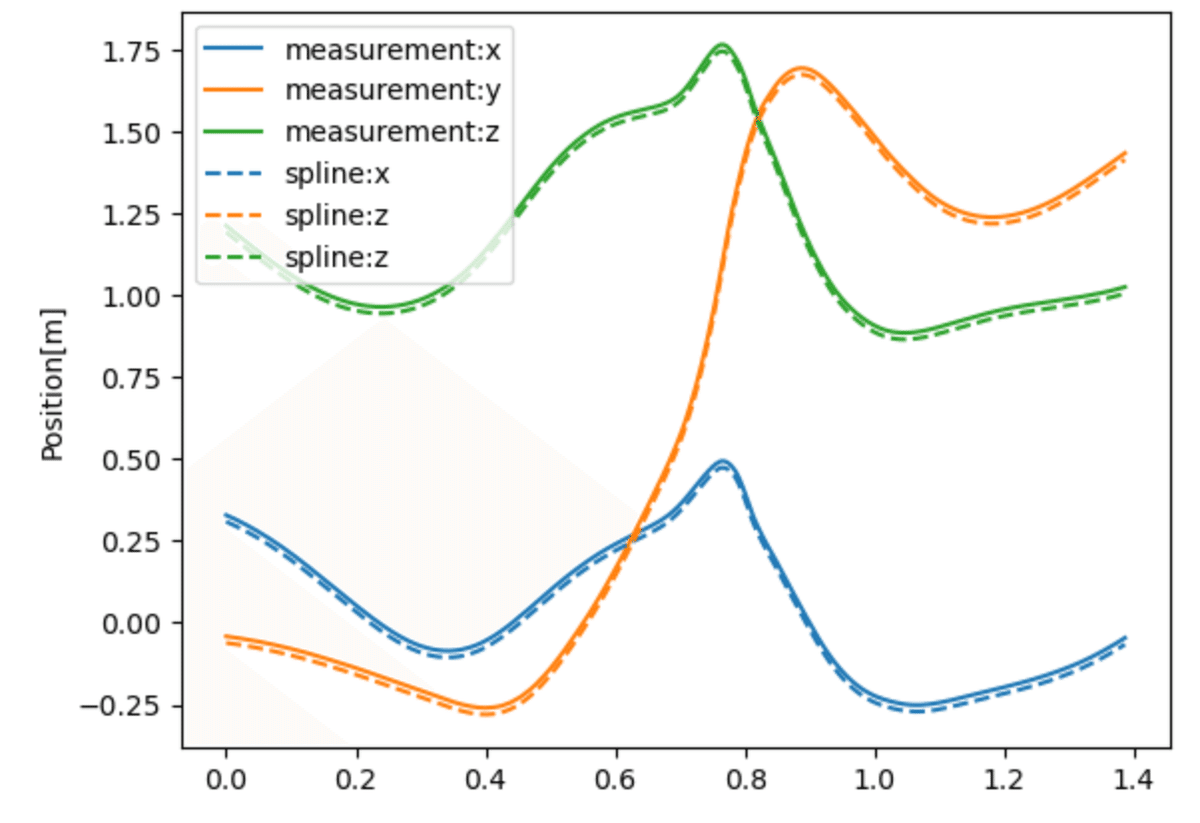
→ ほとんど差が見られない.
そこで,それらの差分を下記のように計算すると,
plt.plot(time, y - smoothing_spline(y, .00001, 360., order=0), lw=.9)
plt.xlabel('Time [s]')
plt.ylabel('Error [mm]')
plt.legend(['x', 'y', 'z'], loc='best')
のように最大でも約1 [mm],各軸とも平均で約0.10 [mm]を示す.平滑化後のデータと観測データとの差分がかなり小さくても,すなわち,それほど強いフィルタリングを施さなくても,適切な加速度計算を実現していることを示している.バターワースのローパスフィルタをどのように適切に設定しても,このような結果を得ることは難しいと思われる.
設定によっては,さらに良い結果が得られるかもしれないが,できるだけシャープな加速度波形を得られるように遮断周波数を20Hzに設定したバターワースのローパスフィルタの結果(x軸データ)では,

最大で6 [mm]程度,平均で0.61 [mm]程度の誤差が発生する.
同様にx軸で,平滑化スプラインとバターワースフィルタによる処理を行い,加速度を比較すると

のような結果となる.あまり運動をしていない最初と最後は滑らかに推移しているはずだが,バターワースフィルタの結果は振動的で,反対に加速フェースは鋭く加速度が変動してほしいが,バターワースフィルタは滑らかにしすぎている傾向がある.もともとノイズの少ない条件で計測しているので,それほどおおきな違いは生じていないが,より悪条件になるとこの実力差は顕著となる.
まとめ
繰り返しになるが,観測データから平滑化スプラインを通して計算されるのは関数(曲線)$${f(t)}$$である.その関数$${f(x)}$$に対して数学的に厳密な導関数(微分)$${\frac{d^2f(t)}{dt^2}}$$を計算し,そこから加速度を計算しているので,位置,速度,加速度間に数学的に厳密な関係が保たれており,これらを繰り返し利用して計算する逆動力学計算に向いている.
このように微分を正確に計算することができるが,数値微分と周波数ベースのフィルタリングでは,フィルタリングと微分のたびに誤差が発生し,誤差と誤差の掛け算を繰り返すことになる.
どれほど実際の加速度と異なるかの検証が困難なため,気に留めない方も多いと思うが,加速度計算は力学計算の精度を左右するため,一度加速度センサと比較するなどの検証を行ってみると良いだろう.
平滑化スプラインのよいところだけ述べてしまったが,決して万能ではないので,以下に注意点をまとめる.また,そもそも計測データの質がpoorであれば限界がある.できるだけよい計測を行うことが基本である.
平滑化スプラインの特徴・注意点
平滑化スプラインは関数近似のため,モーションキャプチャのデータのように多少データの欠損データ(Nan)があっても構わない.ただし,加速度の計算の場合は,4次以上の関数で記述する必要がある.
平滑化スプラインの性能のについては,使用してみれば一目瞭然であるが,いくつか不都合な点もあるので下記にまとめる.
重み係数の決定
$${\lambda}$$の決定方法が試行錯誤的になる.これはデータの長さや,データの暴れ具合で適切な値が変化するため,たとえば,同じマーカの位置ベクトルであろうと,特に暴れる方向があれば,3次元の軸成分によっても重み係数を変化させる必要があるときも生じる.
同じマーカでも,フィルタリングするデータの長さにも依存する.図9のように$${\lambda}$$が.00001のようなときもあれば,100などの数値が適切なときもある.変化の仕方が大きいので,注意深く選択する必要がある.$${\lambda}$$を変化させながら図9のようなグラフを描きつつ,図10のようにデータの近似度が大きくずれていないことを確認することで,適切な$${\lambda}$$を選択するしかない.UnivariateSpline()のsのオプションを空欄にし自動的に$${\lambda}$$を選択はしてくれるが,信頼しないほうが良い,
ただし,これは周波数ベースのフィルタリングにおける,適切な遮断周波数の選択においても試行錯誤的になってしまうことと本質的に違いはない.
オフライン計算
周波数ベースのフィルタリングは,数値に係数を乗算するだけの計算のため,時間遅れは生ずるがオンラインで計算する事ができる.しかし,平滑化スプラインは,全データを使用する最適化計算によって計算するため,オフラインの計算となる.
計算負荷
平滑化スプラインの計算は,連立方程式,すなわち行列の計算にいきつく.このためデータ数が大きくなると,行列演算の負荷が大きくなり,計算が急に重たくなることがある.メモリの使用も増える.データの暴れ具合にもよるが,たとえばモーションキャプチャで長い時間の計測を行った場合にはメモリ不足で,計算ができなくなることもある.
収束性
最適化計算をしている以上,データが暴れ具合によっては収束しないこともある.多くの場合,適切な平滑化パラメータ$${\lambda}$$が選択できていないか,適切なデータが計測できていないことを意味する.
着地衝撃など運動の質が途中で劇的に変化する場合などにも,注意されたい.
観測データの末端
周波数ベースのFIRやIIRフィルタなどは,畳み込み計算による端点でのデータが欠損する.これは短いデータでは深刻な問題となる.これに対して平滑化スプラインでは欠損は生じないが,端点でのデータの暴れ具合の影響を強く受けるので,注意が必要である.
そのような場合には,分割して計算を行うなどの工夫が必要となる.
また,平滑化スプラインはデータの欠損(Nan)にも対応するが,データ端点(最初と最後)に欠損(Nan)がある場合,計算ができないので注意されたい.
次章について
次章では,フォースプレートのデータや,平滑化スプラインを利用した加速度データを取りこんで関節に作用する力を計算し,ニュートンの運動方程式の計算を完成させる.
マガジン「動かして学ぶバイオメカニクス」


【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
