
動かして学ぶバイオメカニクス #16 〜動力の伝達〜
特にロボットの運動との対比を考えると,恐らく身体運動を最もヒトたらしめるものは効率で,運動を行う上でこの呪縛からは逃れられないだろう.ただし,身体の運動における効率を考える上で,一般に機械工学などが定める効率の定義は役立たない.ここではエネルギーの時間微分が力と速度の内積で記述されことを利用して,身体運動における効率を考えるいとぐちについて述べていく.
はじめに
エリートアスリートのダイナミックな動きは発揮する力の強さの賜物だろう.しかし,これまで述べてきた運動方程式を用いた解析による「力発揮の大小」だけでは運動の良し悪しを判断することは難しい.なぜなら,発揮した力が有効活用されていない可能性もあるためだ.エリートアスリートの洗練された動きの中に「無駄の無さ」を感じることも多いのではないだろうか.これは単に大きな力を発揮した結果だけではないはずだ.
そこで,発揮した力の有効利用という尺度が運動の質を判断する材料となり,効率という概念が必要となることが示唆される.そこで無駄のない動きや洗練された動作のメカニズムを理解する道具としての効率を考え,議論の糸口となる数学的な道具をここで示していきたい.
機械工学的な観点から身体運動の効率を考える上で,有効なひとつの方法は力学的エネルギーを導入することである.エネルギーは生理学的なエネルギーや,電気的エネルギー,流体のエネルギーなどにも都合よく変換ができ,エネルギーベースで生理学的エネルギー供給機構と力学的エネルギーの関係を数理で記述し,マラソンや長距離の最適ペース配分なども議論できる(文献1).つまりエネルギーベースの数理を利用すれば生理学とバイオメカニクスを融合することも可能となる.もちろん他の分野の問題を数理で記述し融合した議論も可能だ.
図1には力学的なエネルギーを流体の流れに例え,身体の各部位間の力学的エネルギーの移動を流れとして可視化した例を(文献2)に示した.

これは単にエネルギーの移動(流れ,供給等)を示したものだが,たとえばエネルギーが増加した部位はおおよそ運動エネルギーも増大すると考えて良いので,速度を増加させる効果があると考えてよい.ただし線形ではない.速度の二乗で運動エネルギーが定まるので,運動エネルギーが2倍でも速度は$${\sqrt{2}}$$倍となる.
エネルギーの概念を利用すると,力学の「力と速度」は,電気の「電圧と電流」,流体(水)の「ポンプによる汲み上げと水流」などに置き換えることができる.そこで,身体運動における力学的エネルギーも流体に置き換えることで,エネルギーの流れを増やす方略が見えてくる.たとえばポンプの力を増大させることはもとより,水路の幅や「抵抗」を減らすことで流量が変化する.いくらポンプの力が強くても,伝送路の抵抗が大きくては水が流れない.つまり抵抗の変化から身体運動におけるエネルギーの伝達量を増やす戦略が見えてくる.一般に,このような抵抗はインピーダンス(impedance)と呼ばれる.身体運動におけるインピーダンスを観察したり,それを変化させる数理を理解することが,効率の良い運動を理解するヒントになるだろう.
後ほどの章でこのようなエネルギーの伝達やインピーダンスを可視化する方法を示す予定だが,しばらくの間はエネルギーの効率の良い流れを引き起こす数理を理解する準備を行うことが目的となる.
運動の拘束
このシリーズではこれまでに,関節に作用するトルクや力を計算する方法論と,身体運動におけるその物理的意味について述べてきた.第14章では,運動方程式からの考察から,むしろ関節を動かさずに動力を生み出していることも述べた.このことからトルクはむしろ間接的に運動に貢献していることが示唆されている.
このような考えを導のが力学解析で,計測した「運動」から運動方程式を介して身体に作用する力や「トルク」を逆動力学解析と呼び,反対に「トルク」から運動方程式を介して「運動」を生成する流れを順動力学解析と呼ぶ.逆動力学は,単なる運動学データなどの代数計算であるが,順動力学では一般には数値シミュレーションが必要となる.運動方程式は先程述べた力と速度を関係づける方程式の役割を果たしている.このように「運動方程式」を媒介することで,入力であるトルクと出力である運動間の関係を記述することができ,トルクや力と運動間の因果関係を論じるだけなら,それだけで事足る.
また,トルクの関節まわりの貢献だけでなく,全身の系を考えて積算することで関節に作用するトルクの貢献に還元しようとする方法論もある.ただし,明らかに出力が弱く,外力に近い末端の部位のトルクの貢献が大きいという矛盾した結果が得られ,常識的な解釈とは真逆の結果が得られることからも,運動方程式だけで身体運動を理解するには無理がある.
やはり単なるトルクの大小だけで,運動スキルの巧みさやこつを見出そうとするのは危険だろう.また,運動方程式だけではヒトがなぜそのようなトルクを発揮して運動を行っているか,さらにはエリートアスリートや巧みなスキルを導く「規範」が見えてこない.ヒトらしい運動を支配する規範を考える方法論のピースの中になにかが欠けている.
緩い拘束
バイオメカニクスでは昔から,関節に作用する力ベクトルと関節の速度ベクトルの内積で記述する「力学的エネルギーの時間微分」を用いた解析が行われてきた.これは力学では仕事率(power)に相当し,スポーツバイオメカニクスではそれをパワーと呼ぶことが多く,機械システムでは動力と呼ぶことが多い.
力学的エネルギーの時間変化は,単位時間あたりのエネルギーの「伝達(流れ,移動)」を意味し,その他,エネルギーの「供給」や「吸収・消散」も記述でき,バイオメカニクスでは身体運動における動力生成と伝達のメカニズムを明らかにすることに貢献してきた.図1で示したように,エネルギーの流れを観察することで,どこでエネルギーが湧き出し,どこへ伝達されているかを観察できる.
「運動方程式」は力学法則であり,物理現象はこれに必ず従う.これは強いというより支配的な拘束であるが,「効率」はエネルギーの有効利用という緩い拘束ではあるが,それがどの程度運動を強く拘束しているかを考えていきたい.
いずれにせよエネルギーの流れを導入したとしても,規範を考えていく上でエリートアスリートや巧みなスキルを持つヒトの教師データだけを拠り所にすると,「良しとされる運動」を実現する物理的規範やメカニズムが見えてこない.単にトルクやエネルギー変化の大小と,ヒトが主観的に良しとする教師データ(お手本)だけを拠り所にする議論の仕方は,いろいろな意味で多くの誤りを誘導してきたので注意が必要である.ヒトが行う運動は多様である.冗長性もあり,戦略も多様だ.そこで,身体運動における効率の意味を数理的に考えていくことが重要となる.
動力の生成と伝達効率:効率と抵抗
明確な定義があるわけではないが,機械工学で定義される一般的な「効率」は,
$$
\frac{出力}{入力} = \frac{入力 - 損失}{入力}
$$
のように,与えたエネルギー全体から損失したエネルギー分をさし引いた有効利用されたエネルギーと,エネルギー全体との比で表す.これはトータルのエネルギー(仕事率の積分)を観察した尺度で,ヒトの運動の効率をこれで考えることは少々荒っぽい議論である.途中経過はなんでもよいから,運動のトータルとしての仕事の成果を基準にしている.
そこで,身体運動の物理的規範を考えていく上でヒントとなるのが前述の力学的エネルギーの時間変化である.つまり仕事を時間微分した仕事率を導入するが,これはよく知られているように,力ベクトルと速度ベクトルに分解できる.この力と速度の比はインピーダンス(impedance)と呼ばれ,動力伝達の「抵抗」を意味し,運動の「状態」をこの力と速度で記述することで,動力を効率よく伝達できる良い状態というものを記述できる.
また,力学的エネルギーやその時間微分の仕事率はスカラーであるが,力と速度に分解してしまえば,ベクトルでの議論が可能となる.つまり,運動や力の方向(成分)との関係での議論も可能となる.
簡単な例を上げれば,たとえ大きな力と速度が発揮されても,それらのベクトルが直交していてはエネルギーは変化しないので,どちらかに合わせて力や速度を増大させることが重要となる.このような考え方を用い,仕事率をさらに速度と力で運動の状態を記述することで,つまりエネルギーをさらに力と速度に分解することえ,動力伝達の意味での効率を記述することができそうだ.
ここでは単位時間あたりの効率を力と速度で考えていく.その積分(総和)が最大効果となる保証はないが,身体に過大な負荷をかけないヒトらしい運動の原理が見えてくるかも知れない.
質点と多体系の力学的エネルギーの時間変化と動力伝達
身体運動の効率を考えていく上で,数理的な考察の準備を行うため,多体系の運動方程式とその力学的エネルギーの時間変化を導出する.
質点の場合

多体系の例を考える前に,まずは,図2のような質量$${m}$$の運動で,仕事率(エネルギーの時間変化)について整理する.
図2に示すように,もし物体に一定の力$${\bm{F}}$$を与え続け,一方向に$${\Delta \bm{x}}$$だけ移動したとしよう.このときの,仕事は
$$
\Delta W = \bm{F}^T \Delta \bm{x}
$$
で与えることができる.これは力ベクトル$${\bm{F}}$$と変位ベクトル$${\Delta \bm{x}}$$の内積である.ベクトルの転置記号($${{}^T}$$)を利用した,ベクトルの内積表現とその意味については
などを参照していただきたいが,これは力ベクトル$${\bm{F}}$$の変位ベクトル$${\Delta \bm{x}}$$方向に対する射影ベクトル$${\bm{F}'}$$の大きさ$${|\bm{F}'|}$$と,変位ベクトルの大きさ$${|\Delta \bm{x}|}$$の積$${|\bm{F}'| |\Delta \bm{x}|}$$に相当する(図2).したがって力と速度ベクトルの方向が直交すると,物体にエネルギーを供給することができない.実際,等速回転運動を行っている際にはそのようなことが発生し,一定の回転運動を行ったままとなる.

次に,図3のように時間で変化する力を質点に与えた場合を考える.質点は細い破線の経路を動き,その位置を$${\bm{r}(t)}$$とする.質点には時間変化する外力$${\bm{f}(t)}$$が作用し,他に重力$${m \bm{g}}$$も作用する.
ここで,もし変位$${\Delta \bm{r}}$$だけ移動すると,外力$${\bm{f}}$$による仕事は積分を用いて
$$
\Delta W = \int_{\bm{r}} \bm{f}^T d\bm{r}
$$
と記述できる.ここで,質点の速度を$${\bm{v}=\frac{d \bm{r}}{dt}}$$とし,微小変位$${d\bm{r}}$$が
$$
\bm{v}(t) = \dot{\bm{r}}(t)=\frac{d\bm{r}}{dt}
$$
であることを利用すると,仕事は
$$
\Delta W = \int_{t} \left(\bm{f}^T \bm{v}\right) dt
$$
と書くことができ,$${\bm{f}^T \bm{v}}$$を仕事率と呼ぶ.

これは図2で示した時と少し異なるが,図4のようにそれは速度ベクトル$${\bm{v}}$$の力ベクトル$${\bm{f}}$$に対する射影を$${\bm{v}'}$$とすると,$${\bm{f}}$$の大きさと射影ベクトル$${\bm{v}'}$$の大きさの積$${|\bm{f}|~|\bm{v}'|}$$が内積$${\bm{f}^T \bm{v}}$$に相当する.これが位置$${\bm{r}}$$における仕事率である.ここでは事率も破線の経路上で変化しているので,それを経路上で加算したものが,力$${\bm{f}(t)}$$が質点に与えた仕事$${\Delta W}$$となる.
これは経路上で移動している間に,変化させたエネルギーの変化分$${\Delta E}$$に相当し,このエネルギーの変化をもたらすのが仕事$${\Delta W}$$である.また,単位時間あたりにどの程度エネルギーの時間変化(時間微分)を与えているかを示しているのが仕事率である.電気における電力に相当する.
力学的エネルギーから導く仕事率
仕事を定義し,それを積分するとエネルギーの変化分に相当することを示した(定義)した.
これとは反対に,力学的エネルギーをまず定義し,その時間変化(時間微分)から仕事率を導いてみよう.このような計算は後ほど多体系でも行う.
図5に示した質点の運動方程式は外力$${\bm{f}}$$と重力$${m\bm{g}}$$が作用するので,

$$
m \frac{d \bm{v}}{dt} = \bm{f}+m\bm{g}
$$
となり,この質点の力学的エネルギーは
$$
E = \frac{1}{2}m\bm{v}^T \bm{v} - m \bm{g}^T \bm{r}
$$
と書くことができる(補足1).そこで,これを時間微分すると,
$$
\dot{E} = \frac{dE}{dt} = m (\frac{d\bm{v}}{dt})^T \bm{v} - m \bm{g}^T \bm{v} \\
$$
が得られるが,先程の運動方程式を利用すると,
$$
\bm{f} = m \left(\frac{d \bm{v}}{dt} - \bm{g} \right)
$$
なので,
$$
\frac{dE}{dt} = m (\frac{d\bm{v}}{dt})^T \bm{v} - m \bm{g}^T \bm{v} \\
= m \left(\frac{d \bm{v}}{dt} - \bm{g} \right)^T \bm{v} \\
= \bm{f}^T \bm{v}
$$
となり,力学的エネルギーの時間微分が外力$${\bm{f}}$$と質点の速度$${\bm{v}}$$との内積で記述でき,さきほど導入した仕事率と一致することが確認できる.
すなわち,重力が作用していても,系(ここでは質点)に加えた外力(ベクトル)$${\bm{f}}$$とその外力を加えた位置の速度ベクトル$${\bm{v}}$$との積(ベクトルの内積)$${\bm{f}^T \bm{v}}$$が,仕事率(パワー)となる.このようには,運動エネルギーと位置(ポテンシャル)エネルギーの和である力学的エネルギーの時間変化(時間微分)からも導くことができる.
このように,物体に加えた外力と速度の積が,物体のエネルギーの単位時間あたりの変化を記述し,それが仕事率である.これは機械系では動力となり.電気系では電力(単位W:ワット)に相当する.
図6にエネルギーを流体に例えたエネルギーの流れのイメージを示した.

コップに溜まっているのがエネルギーで,コップからは単位時間あたりのエネルギーの供給と消散があり,それによって単位時間あたりエネルギー量が変化する様子を流体の流れで示した.この出入りしている流れの単位時間あたりの量が仕事率に相当する.ここで,コップは質点や身体の各部位と考えればよいだろう.
また,力学的エネルギーは運動エネルギーだけでなくポテンシャル(位置)エネルギーも含むが,溜まっている流体の量が多いほど,線形ではないが運動速度が大きくなると考えてよいだろう.
多体系(2リンク機構)の場合
質点の例では,一つの質点に一つの外力を加えたが,身体のように複数の剛体に複数の力が与えられる場合を考えていく.
全身の系を考えた場合,加えられる力は,関節に作用する並進力と回転の力(トルク)の二種類であった.それぞれの力で身体各部のエネルギー変化への貢献の役割が異なる.詳細は後述するが,関節に作用する力は部位間の動力を伝達する役割があり,身体間のエネルギーの移動(流れ)に寄与する.一方,関節のトルクは,そこから動力を供給したり,運動を止めるようにエネルギーを吸収する役割がある.
スポーツバイオメカニクスでは,前者を例えば関節力パワー(英語ではjoint power),後者を関節トルクパワー(muscle power)などと呼んでいるようだが,用語がまちまちでここでは使用しない.
図7にはゴルフクラブと腕から構成される2リンク機構を考え,腕とクラブに寄与する4つエネルギーの流れのイメージを示した.
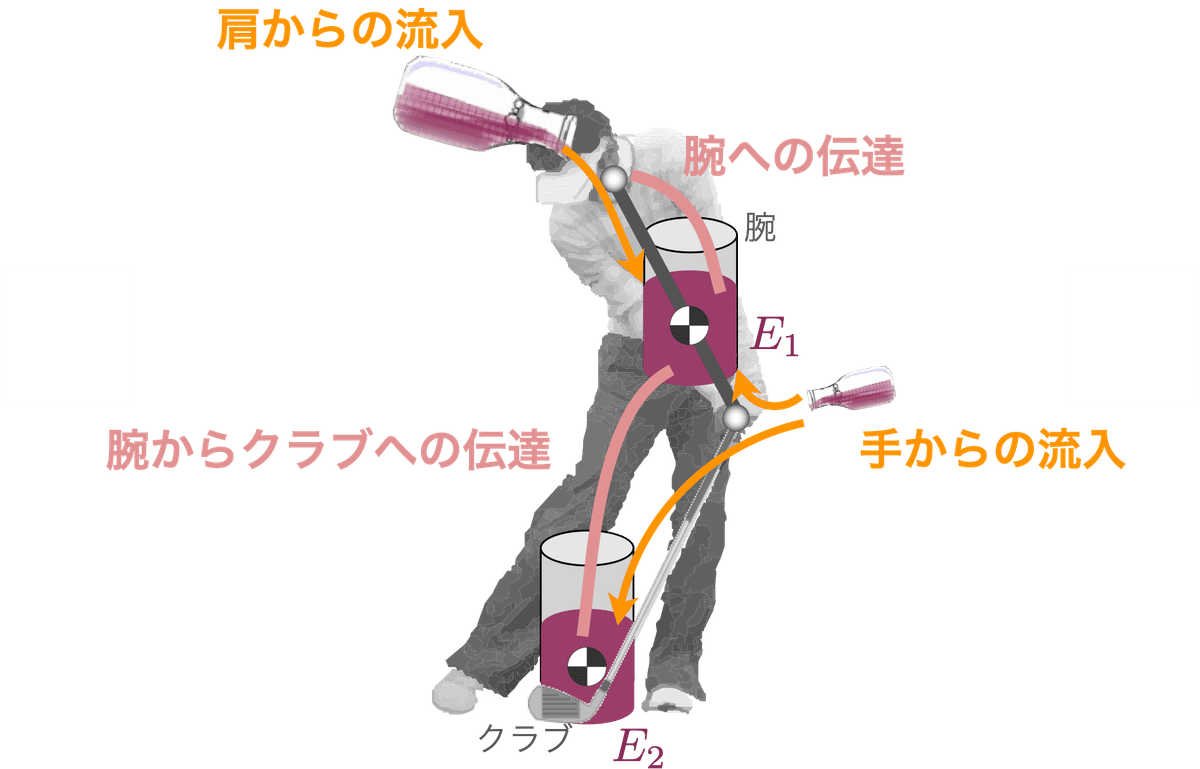
ここで,筋力によるエネルギー供給(または吸収)は瓶からの液体の注入に例え,オレンジ色の矢印で示した(この場合はすべて供給).また,腕とクラブ間,腕を移動するエネルギーはピンク色で示した.図6と同様に腕やクラブのコップに溜まっている量がエネルギーである.
ここで,手部まわりの筋力はクラブだけでなく,腕にもエネルギーを供給(または吸収)する.また腕とクラブ間はパイプで繋がっており,運動をしている際には,エネルギーの行き来が腕とクラブ間である.ここではエネルギーは主に上から(腕から)下(クラブ)に流れているが,実際には上下は関係なく下から上へ逆流することもある.また,運動を止めたり減速させる場合のように筋肉へ戻ることもある.
以下で,これを具体的に数理モデルで考えていく.
各リンクの力学的エネルギー

ここでは,剛体,特に図8に示すような2リンク機構の仕事率を考える.この機構には外力として各関節に作用するトルク$${\bm{\tau}_1, \bm{\tau}_2}$$と,関節1に作用する力$${\bm{f}_1}$$が作用し,この他に二つのリンク間の関節に力$${\bm{f}_2}$$が作用するとする.ここで注意しておきたいことは,この2リンク機構の系に対する外力は,トルク$${\bm{\tau}_1, \bm{\tau}_2}$$と,関節1に作用する力$${\bm{f}_1}$$だけで,リンク間の関節2に作用する力$${\bm{f}_2}$$は外力ではなく内力である.一見すると違いがないように思えるが,この系全体で力$${\bm{f}_2}$$は作用反作用の力として,反対向きに各リンクに作用し相殺されてしまうため,この系全体には寄与しないという意味が込められている.その意味の詳細は後ほど示す.
ここで,$${m_1, m_2}$$を各リンクの質量,$${\bm{I}_1, \bm{I}_2}$$を各リンクの慣性テンソル,$${\bm{x}_{g1}, \bm{x}_{g2}}$$を各リンクの重心の位置ベクトル,$${{}^1_{g1}\bm{p},{}^2_{g1}\bm{p}}$$をリンク1の重心からみた各リンクの関節への位置ベクトル,$${{}^2_{g2}\bm{p}}$$をリンク2の重心からみた関節2への位置ベクトル,$${\bm{\omega}_1, \bm{\omega}_2}$$を各リンクの角速度ベクトルとする.
また,このシリーズで示してきたように,この系の「並進の運動方程式」は
$$
m_1 (\ddot{\bm{x}}_{g1} - \bm{g}) = \bm{f}_1 - \bm{f}2
\\
m_2 \left(\ddot{\bm{x}}_{g2} -\bm{g} \right) = \bm{f}_2
$$
となり,「回転の運動方程式」は
$$
\bm{I}_1 \dot{\bm{\omega}}_1 + \bm{\omega}_{1} \times \bm{I}_{1} \bm{\omega}_{1} = \bm{\tau}_1 - \bm{\tau}_2 + {}^1_{g1}\bm{p}\times \bm{f}_1 + {}^2_{g1}\bm{p}\times (-\bm{f}_2)
\\
\bm{I}_2 \dot{\bm{\omega}}_2 + \bm{\omega}_2 \times \bm{I}_2 \bm{\omega}_2 = \bm{\tau}_2 + {}^2_{g2}\bm{p}\times \bm{f}_2
$$
となる.
また力学的エネルギーは,運動エネルギー$${T}$$とポテンシャル(位置)エネルギー$${U}$$の和で記述できるので,リンク1の運動エネルギーは
$$
T_1 = \frac{1}{2}m_1 \dot{\bm{x}}_{g1}^T \dot{\bm{x}}_{g1} + \frac{1}{2} \bm{\omega}_1^T \bm{I}_1\bm{\omega}_1
$$
と記述できる(補足2).ここで,右辺第1項は並進の運動エネルギーで,第2項は回転の運動エネルギーを示している.
また,リンク1のポテンシャルエネルギーは
$$
U_1 = –m_1 \bm{g}^T \bm{x}_{g1}
$$
と記述できる(補足2).同様にリンク2の並進の運動エネルギーとポテンシャルエネルギーは
$$
T_2 = \frac{1}{2}m_2 \dot{\bm{x}}_{g2}^T \dot{\bm{x}}_{g2} + \frac{1}{2} \bm{\omega}_2^T \bm{I}_2\bm{\omega}_2
\\
U_2 = –m_2 \bm{g}^T \bm{x}_{g2}
$$
と記述でき,各リンクの運動エネルギーは
$$
E_1 = T_1 + U_1\\
E_2 = T_2 + U_2
$$
となる.
リンク2の力学的エネルギーの時間微分
まず,末端のリンク2の力学的エネルギーを時間微分を考える.末端には関節に作用する力$${\bm{f}_2}$$とトルク$${\bm{\tau}_2}$$の二つのなので,この二つの力がリンク2のエネルギー変化に影響を及ぼし,図9のピンクとオレンジ色の2つのエネルギーの流れを引き起こす.

リンク2の力学的エネルギーを時間微分は
$$
\dot{E}_2 = m_2 \ddot{\bm{x}}_{g2}^T \dot{\bm{x}}_{g2} + \dot{\bm{\omega}}_2^T \bm{I}_2 \bm{\omega}_2 -
m_2 \bm{g}^T \dot{\bm{x}}_{g2} \\
= m_2 (\ddot{\bm{x}}_{g2} - \bm{g})^T \dot{\bm{x}}_{g2} + \bm{\omega}_2^T \bm{I}_2 \dot{\bm{\omega}}_2
\\ =
\bm{f}_2^T\dot{\bm{x}}_2 + \bm{\tau}_2^T \bm{\omega}_2
$$
となる(証明は補足2参照).これは関節2($${\bm{x}_2}$$)に作用する力ベクトル$${\bm{f}_2}$$と関節2の速度ベクトル$${\dot{\bm{x}}_2}$$との内積と,関節2に作用するトルクベクトル$${\bm{\tau}_2}$$と関節2の角速度ベクトル$${\dot{\bm{\omega}}_2}$$との内積で表され,関節2を経由し$${\bm{f}_2^T\dot{\bm{x}}_2}$$と$${\bm{\tau}_2^T \bm{\omega}_2}$$だけリンク2に変化を及ぼすことを意味する(図9).以下にそれぞれの意味を補足する.
関節に作用する力によるエネルギーの移動
このうち$${\bm{f}_2^T\dot{\bm{x}}_2}$$はリンク1から移動してくる(負の場合はリンク1へ移動する)単位時間あたりのエネルギー変化であり,エネルギーの流れであり動力の伝達を担っているが,後ほど詳細を述べる(図9ピンクの矢印).
関節に作用するトルクによるエネルギーの供給,吸収
一方,$${\bm{\tau}_2^T \bm{\omega}_2}$$は関節2まわりの筋力が発揮するトルク$${\bm{\tau}_2}$$によってリンク2に及ぼす単位時間あたりのエネルギー変化で,これは筋力によるエネルギーの供給(動力の供給),またはエネルギーの消散や吸収に相当する(図9のオレンジ色の矢印).後ほど示すが,同じトルク$${\bm{\tau}_2}$$は,リンク1に対しても同時に流れを引き起こす.
リンク1の力学的エネルギーの時間微分
リンク1には4つの力が作用するため,それぞれに関してエネルギー変化が発生する.同様に,リンク1の力学的エネルギーを時間微分は

$$
\dot{E}_{1} = m_1 \ddot{\bm{x}}_{g1}^T \dot{\bm{x}}_{g1} + \dot{\bm{\omega}}_1^T \bm{I}_1 \bm{\omega}_1 - m_1 \bm{g}^T \dot{\bm{x}}_{g1}\\
= m_1 (\ddot{\bm{x}}_{g1} - \bm{g})^T \dot{\bm{x}}_{g1} + \bm{\omega}_1^T \bm{I}_1 \dot{\bm{\omega}}_1
\\ = \bm{f}_{1}^T \dot{\bm{x}}_1 -\bm{f}_{2}^T \dot{\bm{x}}_2 + \bm{\tau}_1^T \bm{\omega}_1 - \bm{\tau}_2^T \bm{\omega}_1
$$
となる.
リンク1に作用する4つの力に関するエネルギー変化のうち,$${ \bm{f}_{1}^T \dot{\bm{x}}_1}$$は関節1で外部から移動してくる(またはリンク1から逃げる)単位時間あたりのエネルギー変化であり,エネルギーの流れである.
リンク1の両端にはトルクが作用するが,$${\bm{\tau}_1^T \bm{\omega}_1}$$は,筋力の発揮によって生じるトルク$${\bm{\tau}_1}$$によってリンク1に及ぼす単位時間あたりのエネルギー変化であり,エネルギーの供給,または消散・吸収であり,$${-\bm{\tau}_2^T \bm{\omega}_1}$$は,同様に筋力の発揮によって生じるトルク$${-\bm{\tau}_2}$$によるエネルギーの供給,または消散・吸収である.
また,リンク間の関節に作用するトルク$${\bm{\tau}_2}$$はリンク1に対して$${-\bm{\tau}_2^T \bm{\omega}_2}$$だけ,同時にリンク2に対しては,$${-\bm{\tau}_2^T \bm{\omega}_2}$$だけ変化を及ぼす.すなわち関節2から同じ筋力によってリンク1と2の両方にそれぞれ別途エネルギー変化(供給,吸収)を与える.
関節に作用する力はエネルギーのトンネルを形成する
内力による動力伝達
二つのリンクには重力を除いて4つの力が作用するが,このうちリンク間に作用する力$${\bm{f}_2}$$に注目する.このあと説明するが,この系全体にとってはこれを内力(internal force)と呼ぶ.

ここで,各リンクのエネルギーの時間変化$${\dot{E}_1, \dot{E}_2}$$を比較すると

であったが,式のピンク色の部分の項が$${\bm{f}_{2}^T \dot{\bm{x}}_2>0}$$の場合は,リンク1から$${\bm{f}_{2}^T \dot{\bm{x}}_2}$$だけ減少し,同じ量のエネルギーの移動が関節2を介して行われる.これは,力$${\bm{f}_2}$$が関節2で作用反作用の力各リンクに作用し,符号が異なるため,同じ大きさだが符号が異なるエネルギー変化$${\bm{f}_{2}^T \dot{\bm{x}}_2}$$を各リンクに及ぼしているためである.
一方,系全体のエネルギー変化は
$$
\dot{E}_1 + \dot{E}_2 = \bm{f}_{1}^T \dot{\bm{x}}_1 + \bm{\tau}_1^T \bm{\omega}_1 + \bm{\tau}_2^T (\bm{\omega}_2 - \bm{\omega}_1)
$$
となり,$${\bm{f}_{2}^T \dot{\bm{x}}_2}$$(ピンク色)の項は消えてしまう.これは系内のエネルギーの移動を示している.関節2に力が作用し動いている限りはエネルギーの移動がある意味,勝手に発生することのに注意をされたい.
トルクによる動力伝達のアシスト
$${\dot{E}_1, \dot{E}_2}$$の個別のエネルギー変化は,トルクと作用する側の部位の角速度との内積で記述できたが,それらの和である系全体のエネルギー変化$${\dot{E}_1+\dot{E}_2}$$は,リンク間の関節2に作用するトルク$${\bm{\tau}_2}$$は,$${\bm{\tau}_2^T (\bm{\omega}_2 - \bm{\omega}_1)}$$で示されるようにリンク間の相対角速度$${\bm{\omega}_2 - \bm{\omega}_1}$$との内積で記述されていることに注意されたい.
このことから,もし各リンクが運動は行っていても,「関節を固定」することでリンク間の相対角速度を小さくする場合は,トルク$${\bm{\tau}_{2}}$$はリンク1と2にエネルギー供給を行うが,それらは系全体(リンク1と2全体)では相殺され,系全体に対するエネルギー変化には影響を及ぼさないことを示している.これは$${\bm{f}_{2}^T \dot{\bm{x}}_2}$$とは異なるメカニズムだが,見かけ上系内のエネルギーの移動が起こる.この場合,筋肉は関節を固定することで,見かけ上のエネルギーの移動をアシストすることになる.
さらに述べるなら,もし関節を固定することに意味があるなら,筋肉で関節を固定するよりも,関節の可動域などを利用して固定してしまうほうが,生理学的エネルギーの消費を抑えられるという意味で有効である.
このようなことを踏まえると,エネルギーの変化の大小だけ観察していると,何が起こっているかわからなくなるので,力と速度に分解すして観察することが必要となるといえる.
なお,一般にスポーツのような運動では,関節のトルクが生成するエネルギー変化は,関節に作用する力による伝達と比較すると小さい.この事実は,筋力(トルク)がエネルギーの生成と消散の機能をにない,関節に作用する力によって「エネルギーや動力の伝達」を行い,筋肉はその関節まわりの運動に影響を及ぼすよりも,それを他の部位へ伝送することで運動を生成していることを示唆している.つまり,ヒトのスケールではひとつひとつの筋肉の動力は弱く,協調し効率よくそれを伝達する戦略が求められているのだろう.昆虫ぐらいのサイズになると恐らくその必要がないのだろう.小さいロボットを動かしている分にはうまくいくが,ヒューマノイドロボットで苦労している理由も恐らくこのことと関係しているのだろう.
内力と外力
リンク間の関節に作用する力$${\bm{f}_{2}}$$は「系全体でのエネルギーの変化に影響を及ぼさない」ため,この場合の系内の関節に作用している力は内力と呼ばれる.一方,系のエネルギー変化に影響を及ぼす力(ここでは$${\bm{f}_1, \bm{\tau}_1, \bm{\tau}_2}$$)は外力と呼ばれる.
エネルギーは,内力を媒介することで関節というトンネルを簡単に行き来することができる.そして,その円滑な流れをお膳立てするのが関節に作用するトルク(筋力)と考えるのがよいだろう.筋肉は収縮しながら(物体を押しながら)エネルギーを生成しつつ,内力によるエネルギーの流れの制御を行うことを,身体全体で協調して機能するように働いていると考えるのが素直ではないだろうか.
身体運動における力学的エネルギー変化の物理的意味
まずは,これまで述べてきたことを簡単にまとめる.
動力は単にエネルギー$${E}$$を系(システム)に供給するだけなく,それが負のとき($${\dot{E}<0}$$)は系からエネルギーを吸収したり,消散することもある.
幸いエネルギーは,機械,電気,流体,熱などでも共通した概念を用いることができ,機械系の問題を電気回路にたとえたり,流体の流れにたとえることができるので便利である.エネルギーの時間変化の単位も機械系,電気系などで異なるが,電気系の電力の単位[W]などが利用されることが多い.
また,エネルギーの時間変化は水の流れに例えることもできる.したがって,力学的エネルギーがある物体からある物体に移動することを,エネルギーの流れと呼ぶ.これはエネルギーの伝達ともいえ.機械系であれば動力の伝達と呼ぶ.
身体であれば,関節に力とトルクが作用するので,関節がエネルギーの出入口となる.後述するが,「関節に作用する力」は作用反作用として隣接する部位に作用し,運動していれば(速度を持てば)エネルギーをそのまま隣の部位に垂れ流しする.さらにエネルギーが増加(を供給)する場合はエネルギーの流入,減少(消散)する場合はエネルギーの流出と呼ぶ.
また,筋力は関節に作用するトルクとして,関節からエネルギーを供給したり,吸収する役割を果たす.これはエネルギーの流れを作ってはいるが,ここではこれをエネルギーの供給・消散と呼び区別する.ちなみに流体では供給を湧き出しと呼ぶ.
関節に作用する力は,ある部位から隣の部位にエネルギーをそのまま垂れ流しする役割があり,まさにエネルギーの流れを生み出す.
一方,関節に作用するトルクは,関節から横入りしてエネルギーを供給したり,吸収する役割がある.消散(吸収)は筋力(トルク)で運動を止めたり,減速させたりすることを表している.
面白いことに身体全体のエネルギー変化を観察すると,一般には関節に作用する力が媒介する身体間のエネルギーの流れ(時間変化)と,トルクが身体の各部位へ供給するエネルギーと比較すると,並進の力による移動が支配的である.このことは第14章でも述べたように,トルクは必ずしも関節を動かすように機能せず,トルクによる単位時間あたりのエネルギー供給からは動力生成の様子は観察しにくい.動力を生成している部位を可視化する仕組みは,別途述べることとする.
スポーツの運動と日常の身体運動
身体運動を研究する分野も線引があり,おのずと研究手法や考え方も異なっている.運動学や力学を観点にする分野にもポーツ科学,神経科学,ロボティクスなど身体運動に関わる分野も多岐にわたる.その中でスポーツという運動は特別な運動と考えがちだろう.
しかし,スポーツにおける運動は身体おいて特別な運動ではく,我々の日常運動の延長に過ぎない.一般にスポーツにおける運動は日常行わない速さや精緻さが求められ,我々ヒトはスポーツと日常の運動に多きな違いを感じるかも知れないが,より速く走ろうとも,より強い力を発揮しても,制御方法が大きく変わるわけではない.分野が異なればアプローチの仕方が異なるのは致し方ないが,スポーツと日常の運動で運動の行い方は共通のはずで,どの分野もなにか運動に対する視点が足りないのではないだろうか?
効率というしがらみ・呪縛も,我々の運動の行い方や運動パターン形成にとって強い拘束となっているという意味で,日常の運動とスポーツの運動間に違いはないと思われる.むしろ,日常の自然な運動における規範,つまり効率を顕在化させるよい良い教師データをスポーツにおける運動が提示してくれるかもしれない.日常動作では洗練された動作というものを特別な所作でもなければ感じることはあまりないだろう.むしろエリートアスリートの運動から,実は日常の動作と共通する運動パターンを形成する原理が見えてくるかも知れない.なぜならヒトや生命にとって効率は生命維持にとって優先順位が高いため,スポーツではそれがより顕在化された身体運動として観察することができるためである.
さらに脱線し,以下の話はほとんど裏付けがなく妄想に近いので,話半分に聞いていただければと思う.スポーツに限らず不器用な動きを示す人もいるが,運動が苦手な人も,実はそのひとなりに効率よく,最適化された運動を行っているのかも知れない.言い換えるならばヒトは効率の悪い運動を行うことが苦手で,身体運動に関しては,その人の能力を最大限活用し,実は効率の良い運動をしているのではないかと予想している.神経系や学習と関連する精緻さには違いが大いにありそうだが,力学的な効率はそれほど違いがないのではと考えている.一見下手くそな投げ方をしている人も,ちょっとしたコツが分からず多少ローカルミニマムに引っかかっていたり,非力な筋力に拘束されてしまい,上手投げることができないだけで,力学的な能力を最大限活用している可能性も否定できない.
つまり効率とはそれだけ生命にとって強い拘束条件で,決してそれほど緩い拘束ではないだろう.
エネルギーの蓄積
ここではエネルギーの生成と伝達について考えてきた.ではエネルギーは蓄積することができるだろうか?バイオメカニクスでは,筋肉が伸張してから収縮する挙動を示す理由として,弾性エネルギーの蓄積などと語られることも多いが,そもそもヒトは力学的エネルギーをそれほど蓄えることができるのだろうか.
筋肉には弾性要素が備わっており,筋の活動レベルが上昇するに連れて,活動する弾性要素が増えることによってスティフネス(弾性係数)も上昇することが知られている.そこで,この弾性要素によって「エネルギーを蓄積し」有効利用するために反動動作を行っているという説明がまことしやかに行われているが,本当だろうか.
筋肉や腱には弾性要素を確かに含む.しかし,この議論を行う上で,制御によってあたかもバネのように振る舞うことで観察される筋肉の弾性的な性質と,筋自体の受動的な弾性特性は区別されるべきだ.
このことを考えていく上でヒントとなるのが,ロボットなどの制御で用いられるインピーダンス制御である,簡単に述べるとマニピュレータの手先で,あたかもボールを握っているような感覚になるような制御を行う方法で,マニピュレータの手先の変位に応じて比例するような力をマニピュレータのアクチュエータ(モータ)で与えさえすれば,マニピュレータからボールのスティフネス(弾性)を感じるようにすることが容易に実現できる.
ヒトの運動もあたかも身体がバネのように振る舞って運動しているように見えることはある.たとえば垂直跳びの床反力と身体重心の振る舞いは,身体全体がまるでバネのようだ.より接地時間の短いリバウンドジャンプでは,さらに硬いバネのように振る舞うが,そのように振る舞う理由はあるが,見かけ上そのように見えるだけである.
もし弾性エネルギーを蓄積できるなら,屈伸状態からジャンプしても同じ跳躍高が得られるであろう.それがポテンシャルエネルギーである.
身体がバネのように振る舞うことには物理的に意味がある.しかし,弾性エネルギーを蓄えると述べるのは言いすぎである.大きな出力を必要とする際,確かに筋肉は一旦伸張され,反動動作が多くの運動で発生する.しかしその反動を必要とする理由は他にあり,弾性エネルギーを多少は利用できるだろうが,それが主たる理由になるとは考えにくい.弾性ではなくむしろ筋肉の粘性の性質や,エネルギーの伝達などに依存することが大きいが,それについてはどこかで述べることとする.
SSC (ストレッチショートニングサイクル),運動連鎖,反動動作など,これらは恐らく本質的には同じ現象であるが,弾性エネルギーはそれを行う本質的な理由ではなく,伸張反射も同様で,理由は他にあるだろう.
次章について
次章では,この章で計算した力学的エネルギーの時間変化を,可視化するコードを示す.また第18, 19章で運動中の力ベクトルと速度ベクトル,さらにはインピーダンスという観点で効率について考えていきたい.
補足
補足1:質点の力学的エネルギーのベクトル表記
速度ベクトル$${\bm{v}}$$,重力加速度ベクトル$${\bm{g}}$$,変位$${\bm{r}}$$
$$
\bm{v} = \begin{bmatrix} v_x\\v_y\\v_z \end{bmatrix}, \bm{g} = \begin{bmatrix} 0\\0\\-g \end{bmatrix}, \bm{r} = \begin{bmatrix} x\\y\\z \end{bmatrix}
$$
を用いて,力学的エネルギー(運動エネルギーと位置ベクトル和)をベクトル表記すると,
$$
\frac{1}{2}m\bm{v}^T \bm{v} - m \bm{g}^T \bm{r} \\
=\frac{1}{2}m [v_x~v_y~v_z]\begin{bmatrix} v_x\\v_y\\v_z \end{bmatrix} - m [0~0~-g]\begin{bmatrix} x\\y\\z \end{bmatrix} \\
=\frac{1}{2}m(v_x^2 + v_y^2 + v_z^2) + m g z
$$
と書くことができる.$${\bm{v}^T \bm{v}=v_x^2 + v_y^2 + v_z^2}$$は,ベクトル$${\bm{v}}$$同士の内積で,$${\bm{v}}$$の自乗を意味する.ここで使用しているベクトルの内積については
などを参照していただきたい.
補足2:剛体の力学的エネルギーのベクトル表記
補足1とほぼ同じであるが,リンク1の力学的エネルギーのうち運動エネルギーはベクトルを使用し
$$
T_1 = \frac{1}{2}m_1 \dot{\bm{x}}_{g1}^T \dot{\bm{x}}_{g1} + \frac{1}{2} \bm{\omega}_1^T \bm{I}_1\bm{\omega}_1
$$
のように記述できる.質点と比べて回転の運動エネルギーも含まれる.
右辺第1項は並進の運動エネルギーで,重心位置のベクトルを
$$
\bm{x}_{g1}=\begin{bmatrix}x_{g1}\\y_{g1}\\z_{g1} \end{bmatrix}=[x_{g1}~y_{g1}~z_{g1}]^T
$$
と表すと,$${\frac{1}{2}m_1 \dot{\bm{x}}_{g1}^T \dot{\bm{x}}_{g1}}$$が
$$
\frac{1}{2}m_1 \dot{\bm{x}}_{g1}^T \dot{\bm{x}}_{g1} = \frac{1}{2}m_1
\begin{bmatrix} \dot{x}_{g1}~ \dot{y}_{g1} ~ \dot{z}_{g1} \end{bmatrix} \begin{bmatrix} \dot{x}_{g1}\\ \dot{y}_{g1}\\ \dot{z}_{g1} \end{bmatrix}=
\frac{1}{2}m_1 \left( \dot{x}_{g1}^2 + \dot{y}_{g1}^2 + \dot{z}_{g1}^2\right)
$$
と記述でき,重心$${\bm{x}_{g1}}$$に関する運動エネルギーとなっていることが確認できる.
同様に,右辺第2項は回展の運動エネルギーで,リンク1の角速度ベクトルと慣性テンソルを
$$
\bm{\omega}_{1}=\begin{bmatrix}\omega_{x}\\\omega_{y}\\\omega_{z} \end{bmatrix}=[\omega_{x}~\omega_{y}~\omega_{z}]^T
\\
\bm{I}_1 = \begin{bmatrix}I_{xx}&0&0\\ 0&I_{yy}&0\\0&0&I_{zz} \end{bmatrix}
$$
とすると,$${\frac{1}{2} \bm{\omega}_1^T \bm{I}_1\bm{\omega}_1}$$が
$$
\frac{1}{2} \bm{\omega}_1^T \bm{I}_1\bm{\omega}_1 = \frac{1}{2} \begin{bmatrix}\omega_{x}~\omega_{y}~\omega_{z} \end{bmatrix} \begin{bmatrix}I_{xx}&0&0\\ 0&I_{yy}&0\\0&0&I_{zz} \end{bmatrix} \begin{bmatrix}\omega_{x}\\\omega_{y}\\\omega_{z} \end{bmatrix} =
\frac{1}{2} \left( I_{xx} \omega_{x}^2 + I_{yy} \omega_{y}^2 + I_{zz} \omega_{z}^2 \right)
$$
と記述でき,回転の運動エネルギーのベクトル表記となっていることが確認できる.
一方,重力加速度を$${g}$$とし,重力加速度ベクトルを
$$
\bm{g} = \begin{bmatrix} 0\\0\\-g \end{bmatrix}
$$
とすると,リンク1のポテンシャル(位置)エネルギーは
$$
U_1 = –m_1 \begin{bmatrix} 0~0~-g \end{bmatrix} \begin{bmatrix}x_{g1}\\y_{g1}\\z_{g1} \end{bmatrix} = m_1 g z_{g1}
$$
と記述でき,リンク1の重心$${\bm{x}_{g1}}$$に関するポテンシャルエネルギーとなっている.
補足3:力学的エネルギーの時間微分
力学的エネルギーの時間微分が力と速度の内積であることは,多くの教科書で書かれているが,多関節運動の場合それほど自明ではないと思われる.以下のように簡単に導くことがことができるが,筆者の知る範囲では,具体的にリンク機構の力学的エネルギーを時間微分を導出し,それが関節に作用する力と速度の内積になることを示したバイオメカニクスの教科書や論文は見当たらない.また,筆者の知る限りでは関節のパワーを世に広めたのはDavid A. Winterであるが,彼の論文にもその導出はみあたらない.その物理的意味を考える上で導出しておくことは重要で,それほど難しくないので,ここで示しておく.
リンク2の力学的エネルギー$${E_2}$$の時間微分$${\dot{E}_2}$$から
$$
\dot{E}_2 = m_2 \ddot{\bm{x}}_{g2}^T \dot{\bm{x}}_{g2} + \dot{\bm{\omega}}_2^T \bm{I}_2 \bm{\omega}_2 -
m_2 \bm{g}^T \dot{\bm{x}}_{g2} \\
= m_2 (\ddot{\bm{x}}_{g2} - \bm{g})^T \dot{\bm{x}}_{g2} + \bm{\omega}_2^T \bm{I}_2 \dot{\bm{\omega}}_2
$$
を得る.ここで,リンク2の重心の速度ベクトルは
$$
\dot{\bm{x}}_{g2} = \dot{\bm{x}}_2 + \bm{\omega}_2 \times (-{}^2_{g2}\bm{p})
$$
と書くことができ,リンク2の運動方程式から
$$
\bm{I}_2 \dot{\bm{\omega}}_2 = -\bm{\omega}_2 \times \bm{I}_2 \bm{\omega}_2 + \bm{\tau}_2 + {}^2_{g2}\bm{p}\times \bm{f}_2
$$
を得ることができるので,これらを代入し,さらに
$$
\dot{E}_2 = \bm{f}_2^T\dot{\bm{x}}_2 + \bm{f}_2^T(\bm{\omega}_2 \times (-{}^2_{g2}\bm{p})) + \hspace{2cm}\\
\hspace{1cm} \bm{\tau}_2^T \bm{\omega}_2 + ({}^2_{g2}\bm{p}\times \bm{f}_2)^T \bm{\omega}_2 - (\bm{\omega}_{2} \times \bm{I}_{2} \bm{\omega}_{2})^T \bm{\omega}_2
\\ =
\bm{f}_2^T\dot{\bm{x}}_2 + \bm{\tau}_2^T \bm{\omega}_2 \hspace{3cm}
$$
を得ることができる.ここで,
ジャイロ項のエネルギー消費は外積と内積の幾何学的な性質から$${(\bm{\omega}_{2} \times \bm{J}_{2} \bm{\omega}_{2})}$$と$${\bm{\omega}_2}$$は直交し,$${(\bm{\omega}_{2} \times \bm{J}_{2} \bm{\omega}_{2})^T \bm{\omega}_2 =0}$$となる.なお,ここでの幾何学的性質とは,外積の性質から$${(\bm{\omega}_{2} \times \bm{J}_{2} \bm{\omega}_{2})}$$は$${\bm{\omega}_{2}}$$に直交する.すると直交するベクトルの内積は零となることを利用している.
以下の式は,スカラー三重積(補足4)から
$$
\bm{f}_2^T(\bm{\omega}_2 \times (-{}^2_{g2}\bm{p})) + ({}^2_{g2}\bm{p}\times \bm{f}_2)^T \bm{\omega}_2 = 0
$$
となることを利用している.リンク1についても基本的に同様である.詳細は文献3を参照されたい.
補足4:スカラー三重積
(加筆 23.01.16)
三つのベクトル$${\bm{a}, \bm{b}, \bm{c}}$$の内積と外積
の計算結果はスカラになるため,これをスカラー三重積(scalar triple product)と呼ぶ.
例えば,$${\bm{a}^T (\bm{b} \times \bm{c})}$$のようにベクトルの内積と外積を使って計算する.この結果は最終的にスカラーになる.
ここで,スカラー三重積を記号$${|\bm{a}, \bm{b}, \bm{c}|}$$と表すことにする.これはベクトル$${\bm{a}, \bm{b}, \bm{c}}$$を並べた行列の行列式と一致することに由来する.
そこで,スカラー三重積を$${|\bm{a}, \bm{b}, \bm{c}| = \bm{a}^T (\bm{b} \times \bm{c})}$$のように定義すると,
行列式の性質から,循環置換(cyclic permutation)($${a \rightarrow b \rightarrow c \rightarrow a}$$ の順番の置き換えを指す)と呼ばれる下記の置き換えが等しくなる.
$$
|\bm{a}, \bm{b}, \bm{c}| = |\bm{b}, \bm{c}, \bm{a}| = |\bm{c}, \bm{a}, \bm{b}|
$$
なお,反対向きの循環は以下のように符号が変わる.
$$
|\bm{a}, \bm{b}, \bm{c}| = -|\bm{c}, \bm{b}, \bm{a}|
$$
また,内積の性質から
$$
\bm{a}^T(\bm{b} \times \bm{c}) = \|\bm{b} \times \bm{c} \| \|\bm{a}\| \cos \theta
$$
となり,スカラー三重積の幾何学的意味は以下のように示せる.
$${\|\bm{b} \times \bm{c}\|}$$は平行六面体の底面積(図12のグレー),$${\|\bm{a}\| \cos \theta}$$は符号付の高さに相当し,スカラー三重積$${\bm{a}^T(\bm{b} \times \bm{c})}$$は$${\bm{a},\bm{b},\bm{c}}$$の張る平行六面体の有向体積(符号付きの体積)となっている.

循環置換で順番を入れ替えても,大きさが同じになることが理解できるだろう.
Pythonの記号計算によるスカラー三重積の確認
ここので述べたスカラー三重積の循環置換や行列式への置き換えなどの数学的性質については,Pythonでも確認できる.
数値であればNumpyで内積や外積などが容易に計算できるが,$${\bm{a} \times \bm{b}}$$のような記号のままの計算はできない.そこで数式処理ライブラリSymPyを使用し,スカラー三重積の性質を確認する.Mathematicaとまったく同じようにとはいかないが,簡単な代数演算なら記号のまま計算できるので,上記の問題をPythonの力を借りて計算可能である.Sympyを利用すれば連立方程式なども解ける.上述のような計算は,自分の手で計算することを推奨するが,検算などに利用すると便利である.
Sympyは通常のデフォルトのライブラリに含まれていないこともあるので.importしてもエラーが出るようであれば,たとえば
pip install sympy
# 環境によってはpip3
# Jupyterなどでは "!pip install sympy" とすることで,インストールできる
# Google Colabでは不要として,ターミナルなどでsympyをインストールし(pipについてはネットで検索されたい),以下のように,
import sympysympyのライブラリを呼び込む.
以下で,Mathematicaのように記号(シンボル)でスカラー三重積の性質を確認する.sympy.symbols()を使い,
(ax, ay, az) = sympy.symbols('Ax Ay Az')
(bx, by, bz) = sympy.symbols('Bx By Bz')
(cx, cy, cz) = sympy.symbols('Cx Cy Cz')のように各変数に記号を割り当てる.例えば,ここでは,変数axにAxを割り当てている.
その変数を使って自由に数式を定義できる.四則演算(+, -, *, /)、べき乗(**)などの演算子はPython標準のものを使う.
ここで,ベクトル$${\bm{a}, \bm{b}, \bm{c}}$$を単に並べた行列
mat = sympy.Matrix([[ax,ay,az],[bx,by,bz],[cx,cy,cz]])をsympy.Matrix()で定義する.この行列の行列式$${|\bm{a}, \bm{b}, \bm{c}|}$$はsympy.det()で
sympy.det(mat)のように計算でき,

と出力される.循環置換が成立するかなどは,ご自身で確認していたただきたい.
以下で,次にスカラー三重積の性質を計算する.
a = sympy.Matrix([ax,ay,az])
b = sympy.Matrix([bx,by,bz])
c = sympy.Matrix([cx,cy,cz])たとえばベクトル$${\bm{a}}$$を表示すると,以下のように$${\bm{a}}$$は縦ベクトルとなっている.
a
次に,ベクトル$${\bm{b}}$$と$${\bm{c}}$$の外積$${\bm{b} \times \bm{c}}$$をcross()で計算すると
b.cross(c)
となり,さらに内積をdot()を使用し,スカラー三重積:$${\bm{a}^T (\bm{b} \times \bm{c})}$$を計算すると(expand()で,式をすべて展開している)
sympy.expand(a.dot(b.cross(c)))
を得て,先程計算した$${|\bm{a}, \bm{b}, \bm{c}|}$$と一致していることが,次のように
sympy.expand(a.dot(b.cross(c))) == sympy.det(mat_abc)確認できる(Trueと出力されれば,等しいことを示している).
頭に叩き込むためには,手を紙の上で動かした計算も行ってほしいが,ご自身で,いろいろと確認を試みてみるとよいだろう.
上記の計算はいつものように,以下のGoogle ColaboratoryのリンクからブラウザでPythonコードを実行できるようにした.なお,ログインするためには,Googleアカウントが必要となるので注意をされたい.
なお,Google Colaboratoryの使用方法は,
を参照されたい.
参考文献
1)高木ら,ランニングにおける最適ペース配分に関する研究―エネルギー代謝からみた数学モデルの構築―,スポーツ産業学研究,Vol.5, No.2, pp 45-54, 1995
https://www.jstage.jst.go.jp/article/sposun1991/5/2/5_2_45/_article/-char/ja/
2)阿江,スプリントに関するバイオメカニクス的研究から得られるいくつかの示唆,スプリント研究,Vol.11, pp.15--26, 2001
3)太田ら,二重振子モデルによるゴルフスイングの数理解析 ,機械学会シンポジウム: スポーツ・アンド・ヒューマン・ダイナミクス講演論文集,C1,2011



【著作権・転載・免責について】
権利の帰属
本ホームページで提示しているソフトウェアならびにプログラムリストは,スポーツセンシング社の著作物であり,スポーツセンシング社に知的所有権がありますが,自由にご利用いただいて構いません.
本ページに掲載されている記事,ソフトウェア,プログラムなどに関する著作権および工業所有権については,株式会社スポーツセンシングに帰属するものです.非営利目的で行う研究用途に限り,無償での使用を許可します.
転載
本ページの内容の転載については非営利目的に限り,本ページの引用であることを明記したうえで,自由に行えるものとします.
免責
本ページで掲載されている内容は,特定の条件下についての内容である場合があります. ソフトウェアやプログラム等,本ページの内容を参照して研究などを行う場合には,その点を十分に踏まえた上で,自己責任でご利用ください.また,本ページの掲載内容によって生じた一切の損害については,株式会社スポーツセンシングおよび著者はその責を負わないものとします.
【プログラムの内容について】
プログラムや内容に対する質問に対しては,回答できないことのほうが多くなると思いますが,コメントには目は通します.回答は必要最低限にとどめますので,返信はあまり期待しないでいただけると幸いです,
「動かして学ぶ」という大それたタイトルをつけたものの,また,きれいなプログラムに対するこだわりはあるものの,実際のプログラミングのスキルは決して高くありません.最下部の方のコメント欄によるプログラムの間違いのご指摘は歓迎します.できるだけ反映します.
【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
【データの計測について】
スポーツセンシング社のスタジオで,フォースプレートやモーションキャプチャを利用した計測も行えます.出力されるデータと,ここで示したプログラム(入力データの取り込み関数を少々改変する必要があるが)で,同様な解析を行えますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
