
動かして学ぶバイオメカニクス #22 〜全身の角運動量とCOP〜
フォースプレートで直接計測される力学量は力と力のモーメントで,これらは身体と地面(フォースプレート)間の相互作用で発揮される力である.そこでフォースプレートの代わりに身体側から相互作用の力とトルクを推定できれば,関節に作用するトルク,COP,摩擦による鉛直モーメントも計算でき,原理的にはフォースプレートいらずの力学計算が可能となる.これを理解し実現するため,ここでは角運動量ベクトルの物理的意味に注目する.(230329更新)
はじめに
合成の角運動量
角運動量(angular momentum)については多くの(スポーツ)バイオメカニクスの教科書でも述べられるが,この計算を必要とする事例はあまり取り上げられず,空中などの全身の角運動量が保存するときぐらいに,この計算が必要とされている印象である.
しかし,運動量$${\bm{p}}$$を時間微分することで並進のニュートンの運動方程式$${\dot{\bm{p}} = \bm{f}}$$を導出できるように,角運動量$${\bm{L}}$$を時間微分すると回転のオイラーの運動方程$${\dot{\bm{L}} = \bm{N}}$$を導くことができるので,単に角運動量$${\bm{L}}$$を数値微分によって計算することで,トルクを計算することも可能だ.つまり,解析的には$${\dot{\bm{L}} = \bm{I} \dot{\bm{\omega}} + \bm{\omega} \times (\bm{I} \bm{\omega})}$$であるが,わざわざ$${\bm{I} \dot{\bm{\omega}} + \bm{\omega} \times (\bm{I} \bm{\omega})}$$の計算を行わなわずに回転の運動方程式における慣性力項が計算可能である.精度的な問題は別として(このほうが安定する可能性も十分ある),これは数値計算上の利点である.

そして,特に威力を発揮するときは,全身,または部分的な合成のダイナミクスの計算だろう.系全体から見ると,関節間に作用するトルクは$${\bm{\tau}_j}$$が相殺され「見えない力」となってしまう(図1).全身の各関節に作用するトルク$${\bm{\tau}_j}$$を計算するなら,これまで示してきたニュートン・オイラー法で逐次的な計算のほうが効率が良い.しかし,全身,または定めた系全体(たとえば全身+バット,右脚だけ)の角運動量を計算することで,むしろこの関節間に作用する力とトルクをすべて隠してしまい,足部と地面間に作用する力やトルク$${\bm{N}}$$だけを推定できる.これは全身のダイナミクスを利用した解析的な計算上の利点であり,第14章
で述べたように,物理的意味が式から見える.
このように,関節間に作用する複数のトルクを計算するためにはニュートン・オイラー法による逐次的な計算が適し,外力(系を定めて,系と環境間に作用する力)だけを計算する場合には全体の角運動量を計算するのが良い(補足1).
そこで,ここでは「合成の角運動量」の物理的意味も考えていく.
さて,あらかじめ強調しておきたいことは,角運動量はベクトルのモーメントであって,座標系の原点$${O}$$(回転の中心)に依存するベクトル量で,「原点」が異なると値が異なるという点だ.これは「モーメント」の性質を考えれば当然である.そこで,ここでは角運動量ベクトル$${\bm{L}}$$の原点を記号で陽に示す場合には,原点$${O}$$の関数として$${\bm{L}(O)}$$と書くこととする.
また,その原点を移動したベクトルのモーメントを考える場合,後述するがそれは平行軸の定理(parallel-axis theorem)によって変換されることにも注意されたい.平行軸の定理は慣性モーメントだけに当てはまる定理ではない.モーメント全般に当てはまる定理である.「モーメント」や「平行軸の定理」については,後ほど過去の記事を参照する.平行軸の定理の理解が,この章全体での最も重要となるので,ぜひここで,よく確認をしていただけたらと思う.
したがって,複数の部位の合成の角運動量は単純な加算ではない.原点を統一して変換してから加算する必要がある.
ここでは,「フォースプレートいらずの力学計算」の目的で合成の角運動量を導出するが,もちろんこれをフィギュアスケートの「全身の角運動量」や,その「回転力の推定」の目的に利用しても良いだろう.また,複数の部位をひとつの物体(身体)として見るという視点で,つまり,身体重心のように,まさに「合成」したひとつの全身として回転運動を観察するという観点で重要である.単に計算ツールのために合成の角運動量を理解するのではなく,全身運動の力学の汎用的な物理的な理解のためにこの章を読んでいただけたらと思う.長くなってしまうが,式の説明はできるだけ省略せずに記述した.
合成の角運動量と地面間に作用する外力
第13章
でも確認したが,全身(合成)のニュートンの運動方程式における外力は,地面と接している場合は床反力(地面反力)に相当するように,全身のオイラーの方程式の外力は地面と身体間に作用する力のモーメントである.これらはフォースプレートで計測される足部と地面間に作用する力と力のモーメントと等価である.
そこでここではフォースプレートからではなく,全身の運動量の時間微分から地面と身体間に作用する床反力を推定し(これはすでに第13章で示した),さらに全身の角運動量の時間微分から地面と身体間に作用する力のモーメントを計算することで,フォースプレートのかわりに力のモーメント,COP,摩擦による鉛直軸のモーメントを推定することを目標とする.
さらに,次章ではフォースプレートの代わりに得られた床反力(地面反力)と力のモーメントから,これまで述べてきたニュートン・オイラーを用いて,関節に作用するトルクを推定することを試みる予定である.
なお,片足接地の場合と異なり,歩行や投球時のように両足が接地するフェーズがある場合は,残念ながら,各左右の足に作用する力と力のモーメントの総和は計算できても,左右の足への分配は原則できない.自転車のように両足,両手,腰で自転車と接するような場合は,全ての外力の計測を行うほうが懸命だろう.そこで,次章で示す予定の実際のデータを用いた計算では,キック動作のように片足しか接地していない場合の計測例を取り上げる予定である.
運動量と角運動量
第7章
でもほぼ同じ内容で記述し,内容が冗長になってしまうが,ここで運動量と角運動量について復習する.
運動量

ニュートンの第二法則(運動の法則)が規定する量として,
質量$${m}$$の物体が速度$${\bm{v}}$$で運動する場合,その物体の運動量(momentum)$${\bm{p}}$$は
$$
\bm{p} = m \bm{v}
$$
として定義される(図2).これは「方向」と「大きさ」の両方を持つ物理量で,運動の勢いを表すとされる.この運動量$${\bm{p}}$$は,速度が変位$${\bm{x}}$$の時間微分であることから,
$$
\bm{p} = m\frac{d\bm{x}}{dt} = m \dot{\bm{x}}
$$
として書くことができ,質量$${m}$$が時間変化しないとすると,運動量$${\bm{p}}$$の時間微分$${\dot{\bm{p}}}$$は,
$$
\dot{\bm{p}} = \frac{d\bm{p}}{dt} = m \frac{d^2\bm{x}}{dt^2} = m \ddot{\bm{x}}
$$
と計算できる.もしこの物体に作用する力を$${\bm{f}}$$とすると,
$$
\dot{\bm{p}} = \bm{f}
$$
と記述でき,これをニュートンの運動方程式と呼んだ.この式は運動量の時間変化を引き起こすのが力であることを示している.
角運動量
モーメント
運動量の時間微分がニュートンの運動方程式に相当する.そこで次に,同様にその回転のバージョンを考える.つまり運動量のモーメントを考え,その時間微分が回転の運動方程式であることを示す.
モーメント自体については
を参照していただきたいが,力学におけるモーメントには「慣性モーメント」,「力のモーメント」が存在するが,「角運動量」もモーメントに含まれる.モーメントは距離と物理量の積を表すが,力のモーメント,角運動量はベクトルのモーメントで,ベクトルのモーメントは
$$
\bm{x} \times \bm{p}
$$
のように外積で記述される.繰り返しになるが,この式からもわかるようにモーメントは「回転の中心(ここでは座標系の原点と呼ぶ)位置に応じて変化する物理量」であることに注意されたい.
質点の角運動量
ここで,先程定義した質点の運動量を利用し角運動量を定義する.原点$${O}$$からみた質点の位置ベクトルを$${\bm{x}}$$とし,その運動量を$${\bm{p}}$$とすると
$$
\bm{l} = \bm{x} \times \bm{p}
$$
を原点$${O}$$まわりの角運動量(angular momentum)と呼ぶ.以後,原点を明示的に示すために$${\bm{l}(O)}$$のように,角運動量が原点の関数として書くこともある.これはベクトル量である.
ここで$${\times}$$はベクトルの外積(outer product)であるが,外積については
なども参照されたい.運動量が運動の勢いを表すとされるが,角運動量は回転の運動の勢いと考えてよいだろう.そもそも「勢い」とは曖昧であるが...

質点の角運動量$${\bm{l}(O)}$$の物理的なイメージを図3に示した.質量$${m}$$の質点の位置は位置ベクトル$${\bm{x}}$$で記述され,運動量ベクトル$${\bm{p}}$$を持つ.角運動量ベクトルは原点$${O}$$からみたベクトル$${\bm{x}}$$と運動量$${\bm{p}}$$との外積で計算され,その大きさ$${|\bm{l}|}$$はベクトル$${\bm{x}}$$と$${\bm{p}}$$が構成する平行四辺形の面積で表される.これは青色の「矢印」で記述される右ねじで回転を表すベクトルである.
質点が角運動量を持つためには,それが特に回転運動である必要はない.たとえ直線運動を行っていても,原点を通る直線運動でなければ,原点$${O}$$に対して,質点は角運動量ベクトルを持つ.$${\bm{x}}$$を半径と呼ぶことがあるが,誤解を生まないように単に原点$${O}$$からの質点の位置ベクトルと考えるのが良い(第7章では半径$${\bm{r}}$$で記述したが,ここでは$${\bm{x}}$$としている.また,ここでの外積の演算が回転運動だけを抽出していることに注意されたい.).また,$${\bm{x}(t)}$$は時間変化を認める.
そこで,運動量$${\bm{p}}$$の時間変化がニュートンの運動方程式であることを思い出し,同様に,角運動量$${\bm{l}}$$を時間微分すると
$$
\frac{d\bm{l}}{dt} = \dot{\bm{l}} = \dot{\bm{x}} \times \bm{p} + \bm{x} \times \dot{\bm{p}}
\\
= m \dot{\bm{x}} \times \dot{\bm{x}} + \bm{x} \times \dot{\bm{p}}
$$
となり,右辺第1項は同じ方向を持ったベクトル$${\dot{\bm{x}}}$$同士の外積で,外積の大きさがベクトルとベクトルが構成する平行四辺形の面積に相当することを考えると,$${m \dot{\bm{x}} \times \dot{\bm{x}}}$$は$${\bm{0}}$$となる.そこで,
$$
\dot{\bm{l}} = \bm{x} \times \dot{\bm{p}} = \bm{x} \times (m \ddot{\bm{p}}) = m \bm{x} \times \ddot{\bm{p}}
$$
を得る.角運動量の時間微分は,運動量の微分である力に対するモーメントに相当する.このことから,これが回転の運動方程式に相当することを予感させてくれる.
質点系の角運動量

次に,図4のような質点系全体の角運動量を考える.質点$${i}$$と$${i+1}$$間には,作用反作用の力$${\bm{f}_i, -\bm{f}_i}$$が作用する.これらは相殺され質点の系全体では外力$${\bm{f}_{ext}}$$だけが残ることになる.系全体から見ると,相殺される力は系全体に対しては仕事を行わず内力と呼ばれる.そこで,質点系全体の角運動量は
$$
\bm{L} = \sum_{i=1}^n \bm{l}_i = \sum_{i=1}^n \left( \bm{x}_i \times \bm{p}_i\right)
$$
となるが,ここでニュートンの運動方程式が
$$
\dot{\bm{p}}_i = \bm{f}_i
$$
であることを思い出すと,質点$${i}$$と$${i+1}$$間で作用する,内力同士$${\bm{f}^{int}_i, -\bm{f}^{int}_i}$$が作る角運動量の時間微分(以後,「角運動量変化」と呼ぶことがある)の和は,
$$
\dot{\bm{l}}_i + \dot{\bm{l}}_j = \bm{x}_i \times \dot{\bm{p}} + \bm{x}_{i+1} \times \dot{\bm{p}}_{i+1}
\\
= \bm{x}_i \times \bm{f}^{int}_{i} + \bm{x}_{i+1} \times (-\bm{f}^{int}_{i})
\\
= (\bm{x}_i - \bm{x}_{i+1}) \times \bm{f}^{int}_{i}
$$
となるが,質点間の位置ベクトル$${\bm{x}_i - \bm{x}_{i+1}}$$と内力$${\bm{f}^{int}_{i}}$$の向きが一致すると考えれば,同じ方向のベクトル同士の外積は$${0}$$となり,内力同士が作る角運動量変化も相殺される.つまり図4の内力に相当する黒とグレーの矢印がつくる角運動量変化の和はすべて$${0}$$となる.
そこで,質点系の外部から作用する外力(複数存在しても良い)$${\bm{f}^{ext}_{i}}$$による角運動量だけが残り,系全体の角運動量変化は外力だけによって記述され,
$$
\dot{\bm{L}} = \sum_{i=1}^n \left(\bm{x}_i \times \bm{f}^{ext}_i \right) = \bm{N}
$$
となる.ここで,$${\bm{N}}$$は外力が原点まわりにつくる全モーメントである.
すなわち,角運動量ベクトルの時間微分に相当し,角運動量に変化をもたらすのが外力としての力のモーメント(トルク)$${\bm{N}}$$である.
剛体の角運動量と慣性テンソル
単なる複数の質点の寄せ集めと異なり,質点間の距離関係が変化せず,変形しない物体を剛体(rigid body)と呼ぶ.ロボットと比べれば身体は柔らかい組織で構成されているが,骨が大きく変形しないことを考え,ロボット同様に関節でつながった複数の剛体から構成された系とみなして解析が行われる.いろいろな誤差を考えると,これはそれほどひどい仮定ではないはずだ.
さて,剛体の角運動量についても,やはり第7章
で詳しく述べたがそれらをここに抜粋する.
ここで考える剛体の角運動量を,剛体を$${n}$$個の質点の集合と考え
$$
\bm{L} = \sum_{i=1}^n \bm{l}_{i} = \sum_{i=1}^n \left( \bm{x}_i \times \bm{p}_i \right) = \sum_{i=1}^n m \bm{x}_i \times (\bm{\omega} \times \bm{x}_i)
$$
を得る.ここで,ベクトル三重積の部分は
$$
\bm{x} \times (\bm{\omega} \times \bm{x}) = [\bm{x} \times ] [\bm{\omega} \times ] \bm{x}
$$
のように書くことができる,ここで右辺の外積は歪対称行列(skew symmetric matrix,歪対称行列)を使用して$${[\bm{a} \times ]}$$のような記述方法を使用している.
なお,$${\bm{x}= [x, y, z]^T}$$とすると,歪対称行列を用いて外積は
$$
[\bm{x} \times ] = \begin{bmatrix}0&-z&y\\z&0&-x\\-y&x&0 \end{bmatrix}
$$
と書くことができ,歪対称行列の構造から
$$
[\bm{x} \times ]^T = \begin{bmatrix}0&z&-y\\-z&0&x\\y&-x&0 \end{bmatrix} = -[\bm{x} \times ]
$$
という関係を導くことができ,このことを利用し剛体の角運動量ベクトル$${\bm{L}}$$
$$
\bm{L} = \sum_{i=1}^n m_i \bm{x}_i \times (\bm{\omega} \times \bm{x}_i) \\ = \sum_{i=1}^n -m_i \bm{x}_i \times (\bm{x}_i \times \bm{\omega}) \\ ~~~~= \sum_{i=1}^n -m_i [\bm{x}_i \times ][\bm{x}_i \times ] \bm{\omega} \\ ~~~~= \sum_{i=1}^n m_i [\bm{x}_i \times ]^T[\bm{x}_i \times ] \bm{\omega}
$$
を得る.ここで,$${\bm{L}}$$の中身について,もう少し詳しく眺めてみる.
剛体では質点は密度$${\rho}$$で均質に連続的に分布していると仮定すると,この離散的な式を,次のような連続的な式で表すことができる.すなわち,
$$
\bm{L} = \int_V [\bm{x} \times ]^T[\bm{x} \times ] \rho dV ~\bm{\omega}
$$
のように微小体積$${dV}$$による体積分で記述する.

そして,その中身を
$$
\bm{I} \equiv \int_V [\bm{x} \times ]^T[\bm{x} \times ] \rho dV
$$
と置くと,角運動量ベクトル$${\bm{L}}$$は
$$
\bm{L} = \bm{I} \bm{\omega}
$$
と書くことができ,この$${\bm{I}}$$を慣性テンソル(inertia tensor)または,単に慣性行列と呼ぶ.
ここで,前述の慣性テンソルの式の積分対象の部分($${[\bm{x} \times ]^T[\bm{r} \times ]}$$)だけを取り出す.位置ベクトル$${\bm{x}_i}$$は$${\bm{x}_i = [x_i, y_i, z_i]^T}$$の成分を持つとすると
$$
[\bm{x} \times ]^T[\bm{x} \times ] = \begin{bmatrix}0&z&-y\\-z&0&x\\y&-x&0 \end{bmatrix} \begin{bmatrix}0&z-&y\\z&0&-x\\-y&x&0 \end{bmatrix}\\ ~~~~~~~~~~~=\begin{bmatrix}y^2+z^2&-x y&-x z\\-y x&z^2+x^2&-y z\\-z x&-z y&x^2+y^2 \end{bmatrix}
$$
となる.
このように慣性テンソルを構成する各要素は,個々の質点の位置の関数となり,その積分で記述される.もし,密度が一定で形状がわかるなら計算によって得ることが可能で、例えば球なら簡単に解析的に得られ,身体のように複雑な形状でも数値的に積分することも可能だ.
精度検証は行っていないので,軽々しくは述べるべきではないが,力学計算を行うだけなら慣性モーメントの精度よりも,そのモデルの使い勝手が重要だろう(補足2).なぜなら,力学解析で誤差が生じる要因は山のようにあり,それは多くの人が比較的無頓着な運動の計測精度やフィルタリングに強く依存し,それと比較し慣性モーメントの誤差の影響はさほど大きくはないだろう.
慣性テンソルの座標変換:
この後に示すことになるが,全身の回転の運動方程式の計算では,絶対座標系で角運動量($${\bm{L}=\bm{I \omega}}$$)の時間微分$${\dot{\bm{L}}}$$を計算する.一方,ここでは明示していないが,まず一次的に各部位$${j}$$に固定された座標で慣性テンソル$${\bm{I}_j}$$を計算していることに注意されたい.これは,第9章
で述べた座標系の定義が,慣性テンソルの計算を意識した構成方法となっているためである.このように慣性モーメントのモデルの定義は,身体モデルを強く拘束し,かなりこれに縛られていると言える(補足2).
このことから,慣性テンソルも絶対座標系に変換する必要性を感じるが,実際には各部位の座標系で角運動量($${\bm{L}_j=\bm{I}_j \bm{\omega}_j}$$)を計算し,各部位の身体座標系$${j}$$から絶対座標系$${O}$$に変換する回転行列$${{}^O\bm{R}_j}$$でそれをまとめて絶対座標系に変換を行えばよい.
このことを以下に示そう.
第17章で述べたように絶対座標系での部位$${j}$$の慣性テンソル$${\bar{\bm{I}}_j}$$は,身体に固定された座標系の慣性テンソル$${\bm{I}_j}$$から
$$
\bar{\bm{I}}_j = \bm{R}_j \bm{I}_j \bm{R}_j^T
$$
のように絶対座標系の慣性テンソル$${\bar{\bm{I}}_j}$$に座標変換される.回転行列$${\bm{R}_j}$$と$${\bm{R}_j^T}$$によるサンドイッチで計算する必要がある.身体に固定された座標系で慣性テンソルは対角成分を持つ単なる対角行列で
$$
\begin{bmatrix}
I_{xx} & 0 & 0 \\ 0 & I_{yy} & 0 \\ 0 & 0 & I_{zz}
\end{bmatrix}
$$
のように記述でき計算負荷も低かったが,絶対座標系から見るとこれはもはや対角行列ではなく,すべての成分をもつ.これは面倒で計算効率を上げにくい.
そこで,この絶対座標系の慣性テンソル$${\bar{\bm{I}}_j}$$と,同じく絶対座標系の角速度ベクトル$${\bar{\bm{\omega}}_j}$$の積によって,絶対座標系の角運動量$${\bar{\bm{L}}_j = \bar{\bm{I}}_j \bar{\bm{\omega}}_j}$$を計算すると,
$$
\bar{\bm{L}}_j = (\bm{R}_j \bm{I}_j \bm{R}_j^T) (\bm{R}_j \bm{\omega}_j) = \bm{R}_j (\bm{I}_j \ \bm{\omega}_j)
$$
を得る.この計算では回転行列は直交行列であるため,$${\bm{R}^T \bm{R} = \bm{E}}$$であることを利用している.ここで$${\bm{E}}$$は単位行列である.
直交行列のこの性質については
をご覧になっていただきたい.
この結果から,慣性テンソルと角速度ベクトルを絶対座標系にそれぞれ変換して計算($${\bar{\bm{I}}_j \bar{\bm{\omega}}_j}$$)しても,結果,それは単にローカル座標系同士で計算して一括して絶対座標系に変換する($${\bm{R}_j (\bm{I}_j \ \bm{\omega}_j)}$$)ことと等価になる.
このことからわざわざ,慣性テンソルと角速度ベクトルを個別に絶対座標系にそれぞれ変換することは「無駄」で,ローカル座標系で角運動量$${\bm{L}_j = \bm{I}_j \bm{\omega}_j}$$を計算し,一括して絶対座標系に変換するほうが効率良いことを示している.参照している文献1では,わざわざ慣性テンソルを絶対座標系に変換しているが,この計算は不要である.
全身の回転の運動方程式
ここでは,身体の各部位の角運動量を合成することで,全身の回転の(オイラーの)運動方程式を導出する.
全身の運動量

このマガジンでは全身は$${n=15}$$個の部位から構成されるモデルを用いているが,全身の運動量$${\bm{P}}$$は,各部位$${j}$$の運動量$${\bm{P}_j = m_j \dot{\bm{x}}_{gj}}$$の総和として
$$
\bm{P} = \sum_{j=1}^n \bm{P}_j = \sum_{j=1}^n m_j \dot{\bm{x}}_{gj}
$$
と書くことができる.ここで,$${m_j}$$と$${\bm{x}_{gj}}$$は部位$${j}$$の質量と重心の位置ベクトルである.また,この時間微分$${\dot{\bm{P}}}$$は全身のニュートンの運動方程式となるので,慣性力の項は
$$
\dot{\bm{P}} = \sum_{j=1}^n \dot{\bm{P}}_j = \sum_{j=1}^n m_j \ddot{\bm{x}}_{gj} = M \ddot{\bm{x}}_G
$$
となり,それは全身の外力$${M\bm{g} + \bm{F}}$$に等しく,
$$
\sum_{j=1}^n (m_j \bm{g}) + \bm{F} = M\bm{g} + \bm{F}
$$
となる.ここで,$${\bm{g}}$$は重力加速度,$${M=\sum_{j=1}^n m_j}$$は全身の全質量,$${\bm{x}_G}$$は身体重心の位置ベクトル,$${\bm{F}}$$は外力の総和(地面とだけ接触している場合は,床反力に相当する)である.結果,全身のニュートンの運動方程式は
$$
\dot{\bm{P}} (=M \ddot{\bm{x}}_G) = M\bm{g} + \bm{F}
$$
となり,全身の運動量の時間微分$${\dot{\bm{P}}}$$は,全身のニュートンの運動方程式を構成することがわかる.
ここでは地面とだけ相互作用があり,第13章
でも推定したが,この全身のダイナミクスにおける外力である床反力(地面反力)をまず推定し,これをニュートン・オイラー法による各関節に作用するトルクを推定する逆動力学計算に利用する.
各部位の角運動量
全身の角運動量$${\bm{L}}$$は各部位$${j}$$の角運動量$${ \bm{L}_j}$$の加算
$$
\bm{L} = \sum_{j=1}^n \bm{L}_j
$$
で与えられる.なお,通常各部位$${j}$$の角運動量$${\bm{L}_j}$$は各ローカル座標系の原点まわりで計算されているので,角運動量ベクトルが座標系の「原点」のとり方に依存するモーメントであることを考慮し,これを統一して絶対座標系の原点$${O}$$まわりのモーメントに変換する必要がある.ただし,ここでは座標系の「方向・姿勢」とは無関係の記述の仕方をしていることにも注意されたい.
各部位$${j}$$の重心$${g}$$まわりの角運動量ベクトル$${\mathcal{L}_j(g)}$$を
$$
\mathcal{L}_j(g) \stackrel{\mathrm{def}}{=} \bm{I}_j \bm{\omega}_j
$$
と定義すると,絶対座標系の原点$${O}$$まわりの各部位$${j}$$の角運動量$${\bm{L}_j(O)}$$は
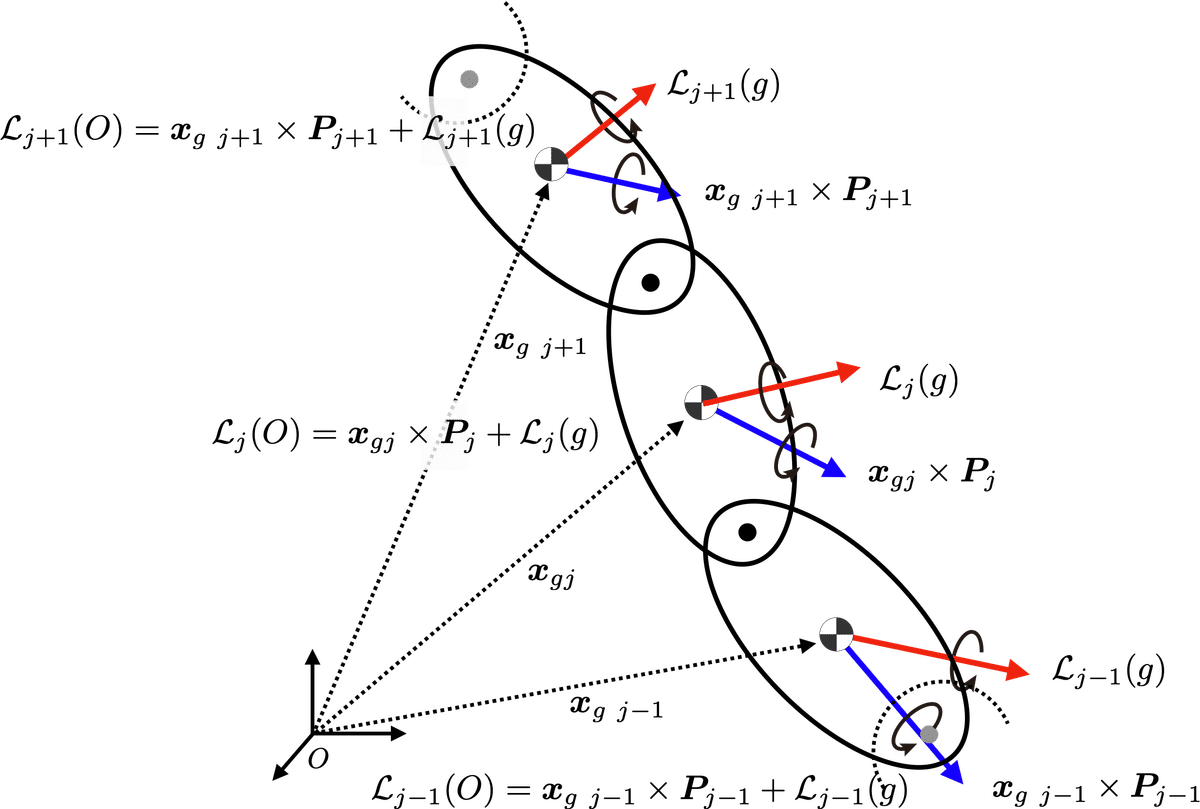
$$
\bm{L}_j(O) = \bm{x}_{gj} \times \bm{P}_j +\mathcal{L}_j(g)\\
= \bm{x}_{gj} \times (m_j \dot{\bm{x}}_{gj}) + \bm{I}_j \bm{\omega}_j
\\
= m_j \bm{x}_{gj} \times \dot{\bm{x}}_{gj} + \bm{I}_j \bm{\omega}_j
$$
のように記述される(図7).ここで,$${\bm{x}_{gj}}$$は絶対座標系から見た,$${j}$$番目の部位の重心位置の位置ベクトル,$${\bm{P}_j}$$は$${j}$$番目の部位の運動量ベクトルである.$${\bm{x}_{gj} \times \bm{P}_j}$$の項は角運動量ベクトルの座標変換のための項で,モーメントの平行軸の定理から計算される.平行軸の定理については
を参照されたい.この各部位$${j}$$の角運動量$${\bm{L}_j(O)}$$を構成する$${\bm{x}_{gj}, \bm{P}_j}$$はモーションキャプチャで計測する場合は通常絶対座標系のまま計算されるが,角運動量$${\mathcal{L}_j = \bm{I}_j \ \bm{\omega}_j}$$はローカル座標系で計算するので,これらを絶対座標系$${O}$$で記述する際には
$$
\bm{L}_j^O(O)
= \bm{x}_{gj}^O \times \bm{P}_j^O + {}^O\bm{R}_j \mathcal{L}_j^j(g)
\\
= \bm{x}_{gj}^O \times \bm{P}_j^O + {}^O\bm{R}_j (\bm{I}_j^j \ \bm{\omega}_j^j)
$$
とすればよい.通常,ベクトル量は座標系のとり方に依存せず成り立つので座標系を明示していなかったが,この式では右上付きの文字が座標系を明示している.以降,必要に応じて位置ベクトルに関してはこのように右上付き文字として座標系を明示して示す.
合成(全身)の回転の運動方程式
全身の角運動量:
以下,文献1を参考に述べる.絶対座標系の原点まわりの各部位$${j}$$の角運動量$${\bm{L}_j(O) = \bm{x}_{gj} \times \bm{P}_j + \mathcal{L}_j(g)}$$を加算した,原点$${O}$$まわりの全身の角運動量は
$$
\bm{L}^O(O) = \sum_{j=1}^n (\bm{x}_{gj}^O \times \bm{P}_j^O) + \sum_{j=1}^n {}^O\bm{R}_j \mathcal{L}_j^j(g)
\\
= \sum_{j=1}^n (m_j \bm{x}_{gj}^O \times \dot{\bm{x}}_{gj}^O) + \sum_{j=1}^n {}^O\bm{R}_j (\bm{I}_j^j \ \bm{\omega}_j^j)
%= \bm{x}_{gj}^O \times \bm{P}_j^O + {}^O\bm{R}_j \mathcal{L}_j^j(g)
$$
と書ける.これは,絶対座標系$${O}$$から見た各部位の角運動量ベクトルの加算である.
図8に,この式の右辺第1項$${\sum_{j=1}^n (\bm{x}_{gj} \times \bm{P}_{j}) = \sum_{j=1}^n (m_j \bm{x}_{gj} \times \dot{\bm{x}}_{gj})}$$の物理的意味を示した.
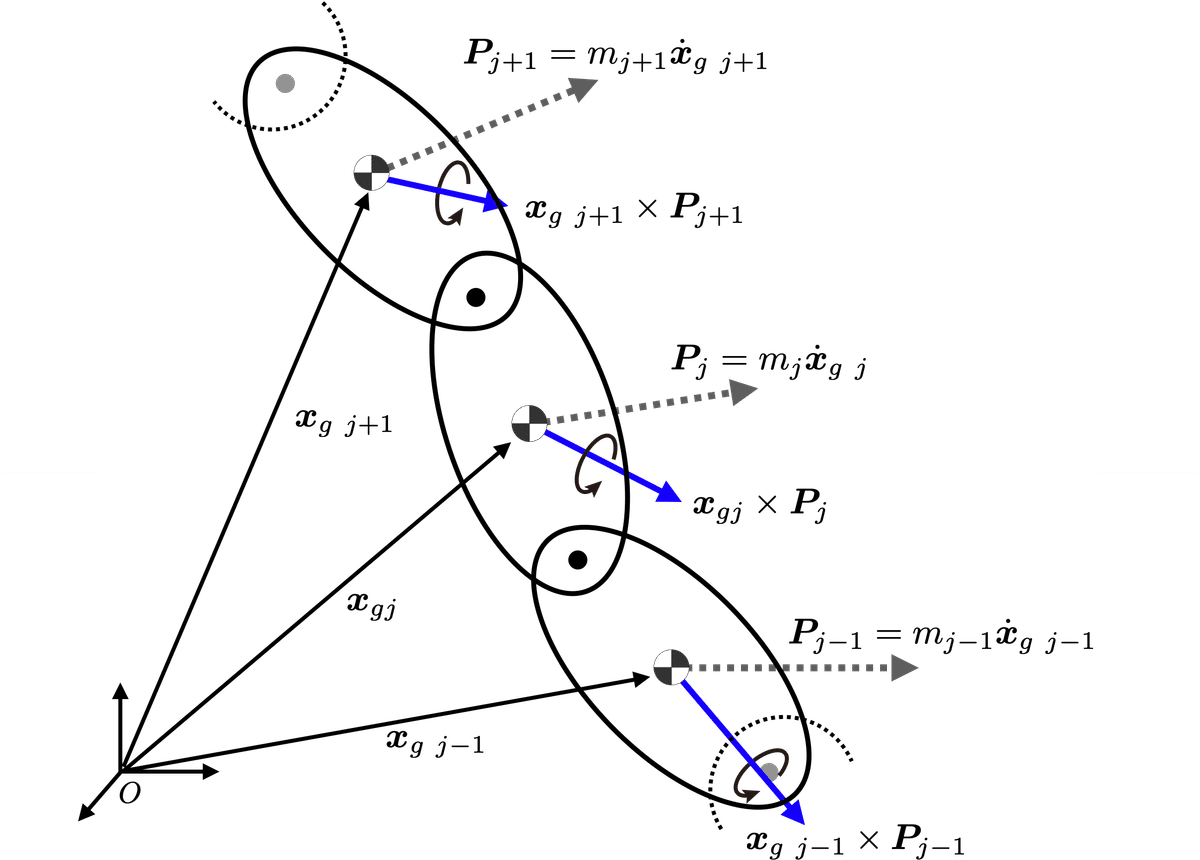
各部位は破線の運動量ベクトル$${\bm{P}_j}$$を持つが,それの原点$${O}$$まわりのモーメント(原点$${O}$$から各部位の重心位置を指す位置ベクトル$${\bm{x}_{gj}}$$との外積)が青色の$${\bm{x}_{gj} \times \bm{P}_{j}}$$で,それを各部位の角運動量ベクトル$${\mathcal{L}_j(g)}$$に足すことで,各部位の重心位置まわりの角運動量から,原点$${O}$$まわりの角運動量に変換できる.つまり,その平行軸の定理による変換のための項を全身分,加算した項である.
全身の角運動量の時間微分:
前述のように各部位の運動量ベクトルのモーメント$${\bm{x}_{gj} \times \bm{P}_j}$$の時間微分は,$${\bm{x}_{gj} \times \dot{\bm{P}}_j}$$なので,絶対座標系の原点まわりの各部位$${j}$$の角運動量の時間微分は
$$
\dot{\bm{L}}_j(O)^O = \bm{x}_{gj}^O \times \dot{\bm{P}}_j ^O+ {}^O\bm{R}_j~\dot{\mathcal{L}}_j^O(g)
$$
となり,
原点$${O}$$まわりの全身の角運動量の時間微分は
$$
\dot{\bm{L}}^O(O) = \sum_{j=1}^n (\bm{x}_{gj}^O \times \dot{\bm{P}}_j^O) + \frac{d}{dt} \left(\sum_{j=1}^n {}^O\bm{R}_j \mathcal{L}_j^j(g) \right)
\\
= \sum_{j=1}^n (m_j \bm{x}_{gj}^O \times \ddot{\bm{x}}_{gj}^O) + \frac{d}{dt} \left(\sum_{j=1}^n {}^O\bm{R}_j (\bm{I}_j^j \ \bm{\omega}_j^j) \right)
$$
と書ける.
全身の並進の運動方程式の慣性力が運動量の時間微分$${\dot{\bm{P}}}$$であるように,全身の回転の運動方程式の慣性力はこの$${\dot{\bm{L}}}$$となる.
また,ニュートン・オイラー法では,内力である関節に作用するトルクを計算するために,$${\bm{I}_j \dot{\bm{\omega}}_j + \bm{\omega}_j \times (\bm{I}_j \bm{\omega}_j)}$$を各部位で計算していたが(補足3),全身では加算した$${{}^O\bm{R}_j \mathcal{L}_j^j(g)}$$を計算し,これをまとめて数値微分(平滑化スプラインなどを使用する)を行えばよいだけだ.数値微分の計算回数が減ることで計算負荷も減る.
全身の回転の運動方程式の外力
絶対座標系の原点$${O}$$まわりのダイナミクス:

一方,地面と足間だけで相互作用する場合,全身の回転の運動方程式における外力(右辺)は,地面と足間で作用する力のモーメント$${\bm{N}}$$と重力$${M \bm{g}}$$による力のモーメントだけなので(図9),全身の運動方程式は
$$
\dot{\bm{L}}(O) = \bm{x}_G \times M \bm{g} + \bm{N}(O)
$$
となる.ここで,$${\bm{N}}$$は原点まわりのモーメントして定義していることにも注意されたい.これより,原点まわりの,フォースプレートの代わりに地面と身体間に作用する力のモーメント$${\bm{N}(O)}$$は
$$
\bm{N}(O) = \dot{\bm{L}}(O) - \bm{x}_G \times M \bm{g}
$$
より得られる.ニュートン・オイラー法と比べると計算負荷が低い.
以上を式にまとめると,まず,絶対座標系$${O}$$で全身の合成の角運動量$${\bm{L}^O(O)}$$の時間微分を前述の
$$
\dot{\bm{L}}^O(O) = \sum_{j=1}^n (\bm{x}_{gj}^O \times \dot{\bm{P}}_j^O) + \frac{d}{dt} \left(\sum_{j=1}^n {}^O\bm{R}_j \mathcal{L}_j^j(g) \right)
\\
= \sum_{j=1}^n (m_j \bm{x}_{gj}^O \times \ddot{\bm{x}}_{gj}^O) + \frac{d}{dt} \left(\sum_{j=1}^n {}^O\bm{R}_j (\bm{I}_j^j \ \bm{\omega}_j^j) \right)
$$
で計算し,
$$
\bm{N^O}(O) = \dot{\bm{L}}^O(O) - \bm{x}^O_G \times M \bm{g}^O
$$
を計算すればよい.
他の点まわりのダイナミクス:

ここでは,絶対座標系の原点まわりのモーメントを計算したが,全身のダイナミクスで必要とされる外力としての力のモーメントは,系外の外部環境と接している部位(例えば足)の重心位置(ここでそれを$${\bm{x}_{gb}}$$とする)まわりの力のモーメントで記述するので,他の原点$${\bm{x}_{gb}}$$まわりのモーメントは,$${\bm{x}_G}$$を$${\bm{x}_{G} - \bm{x}_{gb}}$$に置き換えることで,
$$
\bm{N^O}(\bm{x}_{gb}) = \dot{\bm{L}}^O(\bm{x}_{gb}) - (\bm{x}^O_{G} - \bm{x}_{gb}^O) \times M \bm{g}^O
$$
を計算すればよい.ここで,$${\dot{\bm{L}}^O(\bm{x}_{gb})}$$も
$$
\dot{\bm{L}}^O(\bm{x}_{gb})
= \sum_{j=1}^n \left((\bm{x}^O_{gj} - \bm{x}_{gb}^O) \times\dot{ \bm{P}}_{j}^O \right) + \frac{d}{dt} \left( \sum_{j=1}^n {}^O \bm{R}_j \mathcal{L}^j_j(g) \right)
\\
= \sum_{j=1}^n \left(m_j (\bm{x}^O_{gj} - \bm{x}_{gb}^O) \times \ddot{\bm{x}}_{gj}^O \right) + \frac{d}{dt} \left(\sum_{j=1}^n {}^O \bm{R}_j (\bm{I}_j^j \ \bm{\omega}_j^j) \right)
$$
と置いた.

また,次章で述べるが,これまで第14章
などで述べてきたように,身体運動では$${\bm{L}}$$の回転のダイナミクスで慣性力項$${\mathcal{L}_j(g) = \bm{I}_j \bm{\omega}_j}$$は力のモーメントと比較し小さいことが多く(これを小さくなるように制御することが多く),
$$
\sum_{j=1}^n \left((\bm{x}^O_{gj} - \bm{x}_{gb}^O) \times\dot{ \bm{P}}_{j}^O \right) \gg \frac{d}{dt} \left( \sum_{j=1}^n {}^O \bm{R}_j \mathcal{L}^j_j(g) \right)
%\\
%\sum_{j=1}^n \left(m_j (\bm{x}^O_{gj} - \bm{x}_{gb}^O) \times \ddot{\bm{x}}_{gj}^O \right) \gg \frac{d}{dt} \left(\sum_{j=1}^n {}^O \bm{R}_j (\bm{I}_j^j \ \bm{\omega}_j^j) \right)
$$
が成立する場合は,近似した
$$
\dot{\hat{\bm{L}}}^O(\bm{x}_{gb}) \stackrel{\mathrm{def}}{=} \sum_{j=1}^n \left(m_j (\bm{x}^O_{gj} - \bm{x}_{gb}^O) \times \ddot{\bm{x}}_{gj}^O \right)
$$
を用いても良い.
以上をまとめると,身体と外部環境(例えば地面)間に作用する絶対座標系の$${\bm{x}_{gb}}$$まわりの外力としての力のモーメントは
$$
\boldsymbol{N}(\bm{x}_{gb}) =
+ \sum_{j=1}^n \left((\bm{x}^O_{gj} - \bm{x}_{gb}^O) \times\dot{ \bm{P}}_{j}^O \right) + (\boldsymbol{x}_{G}- \boldsymbol{x}_{gb}) \times M \boldsymbol{g}
$$
となり,前述の近似が成立する場合(または部位で)は,これを近似した,
$$
\hat{\boldsymbol{N}}(\bm{x}_{gb}) = \sum_{j=1}^n \left((\bm{x}^O_{gj} - \bm{x}_{gb}^O) \times\dot{ \bm{P}}_{j}^O \right) + (\boldsymbol{x}_{G}- \boldsymbol{x}_{gb}) \times M \boldsymbol{g}
$$
で計算を行っても良い.
以下に,次章で説明するが,外力としての力のモーメントを計算する関数External_Moment(), External_Moment_approx()の計算ステップをまとめる.
各部位$${{j}}$$の重心の速度ベクトル b_link[j].acc を利用し,各部位の運動量ベクトルの時間変化$${\dot{ \bm{P}}_{j}^O = m_j \ddot{\bm{x}}_{gj}}$$を計算し,それの$${\bm{x}_{gb}}$$まわりのモーメントを加算した$${\sum_{j=1}^n \left((\bm{x}^O_{gj} - \bm{x}_{gb}^O) \times \dot{ \bm{P}}_{j}^O \right)}$$をb_link[1].Resultant_Momentum_Moment() で計算する.
各部位$${j}$$の各部位の座標系の角運動量$${\mathcal{L}_j^j(g) = \bm{I}_j^j \bm{\omega}_j^j}$$を絶対座標系に変換し($${\mathcal{L}^O _j = {}^O\bm{R}_j \mathcal{L}_j^j(g)={}^O\bm{R}_j (\bm{I}_j^j \bm{\omega}_j^j)}$$),これらの全身の加算$${\sum_{j=1}^n \mathcal{L}^O _j}$$をb_link[1].Resultant_Angular_Momentum()で計算する.なお,この項は1と比較し微小なため,省略しても良い.
1と2を加算し,その数値微分$${\dot{\bm{L}}(\bm{x}_{gb})}$$をスプライン平滑化などを利用し計算する.
b_link[1].Resultant_Cg()で計算した合成重心$${\bm{x}_G}$$を,絶対座標系の原点$${O}$$まわりの全身の重力のモーメント$${(\bm{x}^O_G - \bm{x}_{gb}^O) \times M \bm{g}^O}$$をb_link[1].Gravity_Moment()で計算する.関数Gravity_Moment()については次章で説明する.
3と4の結果を利用し,b_link[1].External_Moment()は$${\bm{N}^O(\bm{x}_{gb}) = \dot{\bm{L}}^O(\bm{x}_{gb}) - (\bm{x}^O_G - \bm{x}_{gb}^O) \times M \bm{g}^O}$$より,地面・身体間に作用する絶対座標系の$${\bm{x}_{gb}}$$まわりの力のモーメントを計算する.なお,近似したb_link[1].External_Moment_approx()で$${\hat{\bm{N}}^O(\bm{x}_{gb}) = \dot{\hat{\bm{L}}}^O(\bm{x}_{gb}) - (\bm{x}^O_G - \bm{x}_{gb}^O) \times M \bm{g}^O}$$を計算しても良い.
なお,ロボットなどではオンラインの計算が必要となることから,角運動量$${\bm{L}(O)}$$の数値微分として,単なる差分を用いることがあるが,オフラインの計算が許され,高精度に計算するためには,平滑化スプライン
を使用するのが良いだろう.また,微分を多用するので,バターワースフィルタなどではまともな結果は得られないだろう.
以上から,「全身の運動量」と「全身の角運動量」の項で推定した床反力と力のモーメントを,フォースプレートで計測する床反力と力のモーメントの代わりに使用し,これまで述べてきたニュートン・オイラー法を用いて各関節に作用するトルクを推定することができる.
ここで,注目していただきたいことがある.
$$
\mathcal{L}^O_j \equiv {}^O \bm{R}_j (\bm{I}_j^j \ \bm{\omega}_j^j)
\\
\mathcal{M}_j^O (\bm{x}_{gb}) \equiv (\bm{x}_{gj}^O - \bm{x}_{gb}^O) \times \bm{P}_{j}^O
$$
とすると,近似
$$
\sum_{j=1}^n \dot{\mathcal{M}}_j(\bm{x}_{gb}) \gg \sum_{j=1}^n \dot{\mathcal{L}}_j
$$
が成立するとき,もはや$${\mathcal{L}^O_j \equiv {}^O \bm{R}_j (\bm{I}_j^j \ \bm{\omega}_j^j)}$$の計算は必要ない.つまり慣性モーメントや角速度の計算すら不要である.
あまり,上記の近似が成立するという意味で動力学的に動かない場合,または動かない部位では,回転運動の慣性に関係する計算が不要ということは重要な事実である.
COPと鉛直軸まわりのモーメント
フォースプレートの力学とCOP:
フォースプレートによる計測では,地面と身体間に作用する力$${\bm{F}}$$と力のモーメント$${\bm{N}}$$を利用し,COPと鉛直軸まわりの摩擦のモーメントを計算した.
これに対してここでは,フォースプレートではなく身体側の計測から力$${\bm{F}}$$と力のモーメント$${\bm{N}}$$を推定し,同様にCOPと鉛直軸まわりの摩擦のモーメントを身体側から推定する.
COPと鉛直軸まわりのモーメントの計算の詳細は
を参照していただきたい.

COP(ヒューマノイドロボットで呼ぶところのZMP(zero moment point)と等価)は,地面に作用する床反力$${\bm{F}}$$がつくる力のモーメントの水平成分が$${0}$$となりバランスする位置である(図12).もし片足で接地している場合,これは足裏が地面と接触しているエリア内のどこかに必ずおさまる.
そこで,絶対座標系から見たCOPの位置ベクトルを
$$
\bm{c} = [c_x~c_y~c_z]^T
$$
とし(図12),ここでフォースプレートで計測する力のモーメントを思い出し,絶対座標系の原点$${O}$$まわりでフォースプレート(地面)と身体間に作用する力のモーメント$${\bm{N}(O)}$$をCOPを用いて記述すると
$$
\bm{N}(O) = \bm{c} \times \bm{F} + \bm{\tau}_z
\\
= \bm{c} \times M(\ddot{\bm{x}}_{G}-\bm{g}) + \bm{\tau}_z
\\
=\begin{bmatrix} 0 & -c_z & c_y \\ c_z & 0 & -c_x \\ -c_y & c_x & 0 \end{bmatrix}
\begin{bmatrix} M\ddot{x}_G \\ M\ddot{y}_G \\ M(\ddot{z}_G + g) \end{bmatrix}
+
\begin{bmatrix} 0 \\ 0 \\ \tau_z \end{bmatrix}
$$
となる.ここで,$${\bm{c}}$$は絶対座標系$${O}$$から見たCOPの位置ベクトル,$${\bm{F}=[F_x~F_y~F_z]^T}$$は床反力,$${\bm{\tau}_z = [0~0~\tau_z]^T}$$は鉛直軸まわりのモーメントである(図12).
なお,水平な地面などの場合のように,許されるなら絶対座標系の原点は,地面と同じ高さにし$${c_z =0}$$とするのが簡便である.
身体の力学:
次に,身体側から地面・身体間に作用する絶対座標系の原点まわりの力のモーメント$${\bm{N}(O)}$$を計算する.
ここで,
$$
\bm{L}(O) = [L_x~L_y~L_z]^T\\
\bm{P} = [P_x~P_y~P_z]^T\\
\bm{x}_{G} = [x_G~y_G~z_G]^T\\
\bm{g} = [0~0~-g]^T
$$
のように各ベクトルの成分を定める.そこで力のモーメント$${\bm{N}(O)}$$の各成分は先程示した全身の運動方程式の外力から
$$
\bm{N}(O) = \dot{\bm{L}}(O)- M[\bm{x}_G \times] \bm{g}
\\
= \begin{bmatrix} \dot{L}_x \\ \dot{L}_y \\ \dot{L}_z \end{bmatrix}
-
M \begin{bmatrix} 0 & -z_G & y_G \\ z_G & 0 & -x_G \\ -y_G & x_G & 0 \end{bmatrix}
\begin{bmatrix} 0 \\ 0 \\ -g \end{bmatrix}
$$
となる.
COP:
以上から,COPの概念を利用し,フォースプレート側と身体側から地面と身体間作用する力を計算し,
$$
\begin{bmatrix} 0 & -c_z & c_y \\ c_z & 0 & -c_x \\ -c_y & c_x & 0 \end{bmatrix}
\begin{bmatrix} M\ddot{x}_G \\ M\ddot{y}_G \\ M(\ddot{z}_G + g) \end{bmatrix}
+
\begin{bmatrix} 0 \\ 0 \\ \tau_z \end{bmatrix}
=
\begin{bmatrix} \dot{L}_x \\ \dot{L}_y \\ \dot{L}_z \end{bmatrix}
-
M \begin{bmatrix} 0 & -z_G & y_G \\ z_G & 0 & -x_G \\ -y_G & x_G & 0 \end{bmatrix}
\begin{bmatrix} 0 \\ 0 \\ -g \end{bmatrix}
$$
の水平$${x, y}$$成分を計算すると,
$$
c_y M(\ddot{z}_G + g) - c_z M \ddot{y}_G = \dot{L}_x + M g~y_G
\\
-c_x M(\ddot{z}_G + g) + c_z M \ddot{x}_G = \dot{L}_y - M g~x_G
$$
となり,COPの$${x,y}$$座標$${c_x, c_y}$$について整理すると,
$$
c_x = \frac{-\dot{L}_y + Mg~x_G+ c_z M \ddot{y}_G}{M(\ddot{z}_G + g)}
\\
c_y = \frac{\dot{L}_x + Mg~y_G + c_z M \ddot{y}_G}{M(\ddot{z}_G + g)}
$$
を得る.
$${c_z}$$は絶対座標系から見た床面の高さで,もしモーションキャプチャの座標系と床面が一致しているなら$${c_z = 0}$$とし,
$$
c_x = \frac{-\dot{L}_y + Mg~x_G}{M(\ddot{z}_G + g)}
\\
c_y = \frac{\dot{L}_x + Mg~y_G }{M(\ddot{z}_G + g)}
$$
となる.また身体運動では,
$$
\bm{L}(O) \approx \bm{x}_{G} \times \bm{P}
$$
と近似することができる場合は,
$$
\bm{L}(O) \approx
M \begin{bmatrix}
0 & -z_G & y_G \\ z_G & 0 & -x_G \\ -y_G & x_G & 0
\end{bmatrix}
\begin{bmatrix}
\ddot{x}_G \\ \ddot{y}_G \\ \ddot{z}_G
\end{bmatrix} = M \begin{bmatrix}
-z_G \ddot{y}_G + y_G \ddot{z}_G \\ z_G \ddot{x}_G - x_G \ddot{z}_G \\ -y_G \ddot{x}_G + x_G \ddot{y}_G
\end{bmatrix}
$$
をさらに前述のCOPの式に代入し,
$$
c_x = \frac{-\dot{L}_y + Mg~x_G}{M(\ddot{z}_G + g)}
\\
= \frac{-M(z_G \ddot{x}_G - x_G \ddot{z}_G) + Mg~x_G}{M(\ddot{z}_G + g)}
\\
= \frac{-z_G \ddot{x}_G + x_G \ddot{z}_G + g~x_G}{\ddot{z}_G + g}
\\
= x_G \frac{\ddot{z}_G + g}{\ddot{z}_G + g} - \frac{\ddot{x}_G}{\ddot{z}_G + g}z_G
\\
= x_G - \frac{\ddot{x}_G}{\ddot{z}_G + g}z_G
$$
を得て,同様に,
$$
c_y = y_G - \frac{\ddot{y}_G}{\ddot{z}_G + g}z_G
$$
を得る.
鉛直軸まわりのモーメント$${\tau_z}$$:
同様に,$${\bm{N}(O)}$$の$${z}$$成分を見比べて,
$$
-c_y M\ddot{x}_G + c_x M\ddot{y}_G + \tau_z = \dot{L}_z
$$
を得て,地面と身体間に作用する鉛直軸まわりの力のモーメント$${\tau_z}$$は
$$
\tau_z = \dot{L}_z +c_y M\ddot{x}_G - c_x M\ddot{y}_G
\\
= \dot{L}_z + \frac{\dot{L}_x + Mg~y_G }{\ddot{z}_G + g} \ddot{x}_G + \frac{\dot{L}_y - Mg~x_G}{\ddot{z}_G + g} \ddot{y}_G
$$
となる.
まとめ
ここでは,フォースプレートの代わりに身体側の力学を解くことで,全身の角運動量や,地面と身体間に作用する力と力のモーメント,さらにCOPと鉛直軸まわりの摩擦のモーメントを算出する方法を示した.
この結果を用いれば,フォースプレートによる計測を行わず,これまで述べてきた関節に作用するトルクを計算する逆動力学計算も可能とする.ただし,フォースプレートと精度の比較が必要である.次章以降でも示すが,この十分な検証はまだなされていない.
精度は特にモーションキャプチャや微分演算を含むフィルタなどの計測環境の精度にも強く依存するため,読者自身で確かめられたらと思う.
この方法で推定できるのは,身体全体に作用する力と力のモーメントである.したがって,両脚で接地しているような状況では,力と力のモーメントの左右への分離は基本的にはできない.何らかの仮定や機械学習が必要となる.これも今後の研究に期待している.
回転の中心について:
たとえば,空中期のフィギュアスケートの全身の角運動量$${\bm{L}}$$やジャンプの回転に必要とされる力のモーメント$${\bm{N}}$$は,ここで述べた方法を用いて計算すればよい.ただし,ここで注意しなければ,これらは原点のとり方に依存して角運動量が変化することだ.
フィギュアスケートの空中期の場合,身体重心まわりの角運動量$${\bm{L}(\bm{x}_G)}$$で議論するのが良さそうだが,たとえばハンマー投の加速フェーズなら,どこを原点(中心)とした角運動量を計算するのが良いだろうか?
全身の角運動量を計算した有名な論文でDapena(1989)のハンマー投の研究があるが,これは合成重心まわりの角運動量を計算している. もし,これの時間微分を計算すれば,それは合成重心まわりの回転を行うためのトルクとなる.しかし,それで良いのだろうか?フィギュアスケートなら,身体重心まわりの角運動量を増加させることが一つの課題となが,ハンマー投で重心まわりの角運動量が増加しても,ハンマーの運動量が増えるとは限らない.ハンマー投げの場合,両足で接地している場合があるので,ハンマーの加速を議論するなら,むしろ合成のCOPまわりの角運動量で議論するのが適切だろう.そして,それの時間微分,つまり,ハンマー+全身の系を考えた場合,外力としての力のモーメントは鉛直軸まわりの摩擦のモーメントになる.
単にここで示した計算方法を理解するのではなく,その物理的意味をよく理解してほしい.結果を示すだけではなく,本章では省略せずにその導出を示した理由はそこにある.
次章について
次章
では,本章で述べた数理を,飛び降り動作の実験データ(フォースプレートとモーションキャプチャデータ)を用いて,Pythonコードで検証する.
補足
補足1:内力と外力
内力という用語については,このマガジン「動かして学ぶバイオメカニクス」や「身体のおける運動パターン形成」などでたびたび登場しているが,ここで改めて整理をしておく(図13).内力とは,系を定め,その系内の相互作用の力やトルクであるが,それが相殺され仕事を行わないので,系全体の力学式では相殺され無視してよい力となる.一方,外力は系と外部環境との相互作用のため系に対して仕事を行うことになる.あくまでも系の設定の仕方で,同じ力でもそれは内力にでも外力にもなる.

たとえば,下腿(部位2)の膝関節に作用する力は,系を下腿(部位2),足(部位1)の下肢に設定すれば,これは系と外部環境(この場合,腰部など)との相互作用力となるので外力である.しかし全身を対象とすればそれは,作用反作用の力として相殺される内力である.常に関節に作用する力が内力というわけではない.外部環境から作用する力が外力となる.系の設定仕方で内力と外力は入れ替わり,系に対する仕事の貢献の仕方に注意しながら,内力の意味を理解していただけたらと思う.
図13の例では系は部位1と2に設定され,部位3は外部環境となり,部位2と3間に作用する赤色の力は部位2に作用する力だが,その反作用の力は外部環境の部位3に作用する力で,もはや議論(内力か外力か?)の対象外である.また,系が全身に慣れば部位2と3間に作用する力は内力となる.あくまでも系の定義次第である.
なお,内力は系全体を考えれば無視できる力であるが,系内のエネルギーや運動量の移動には貢献している.系全体ではプラスマイナスゼロの効果だが,身体運動では必要なエネルギーを別な部位に移動させるために貢献する重要な役割を果たす.身体運動では無視してはよろしくない力である.
内力の定義:
内力について,もう少し頭を悩ます具体例を取り上げよう.

図14は物体の左右から異なる大きさの圧縮力が作用していることを示している.ここで外力$${\bm{f}_e}$$は明確で
$$
\bm{f}_e=\bm{f}_1+\bm{f}_2
$$
と記述できる.外力$${\bm{f}_e}$$によってこの物体を動かすことになる.
では,この場合の内力$${\bm{f}_i}$$は具体的にどのように計算されるであろう?関節に作用する力は単に作用反作用の力であるので,そこに作用する力が内力そのものである.しかし,この場合の,仕事に貢献しない力としての内力をどのように計算すればよいか考えてみてほしい.ことはそう簡単ではない.$${\bm{f}_i = \bm{f}_1 - \bm{f}_2}$$だろうか?実は力学用語で,その定義が曖昧なもののひとつが内力である.最初,力学用語で数学的な定義が曖昧な用語が存在することにかなり戸惑ったが,数学的理由からこれは致し方ない.
そこで,それを定める方法のひとつで,実際に部材に作用する内力を計算する方法として,ムーア・ペンローズの擬似逆行列(Moore-Penrose pseudo-inverse matrix)を用いる方法があるが,その方法に従えば(文献2),内力$${\bm{f}_i}$$は
$$
\bm{f}_i = \frac{1}{2}(\bm{f}_1 - \bm{f}_2)
$$
と計算できる.詳細は文献2をご覧になってほしい.
実は力覚センサは外力のセンサではなく,上記で示した内力を測っているので左右の力が異なる場合は,問題になる.左右の力が異なるということは外力が作用し計測対象の物体が運動することになる.力覚センサは運動せず固定されていることが,正しい力を計測する条件となるが,この事実は意外とセンサメーカですら正しく理解されていない.
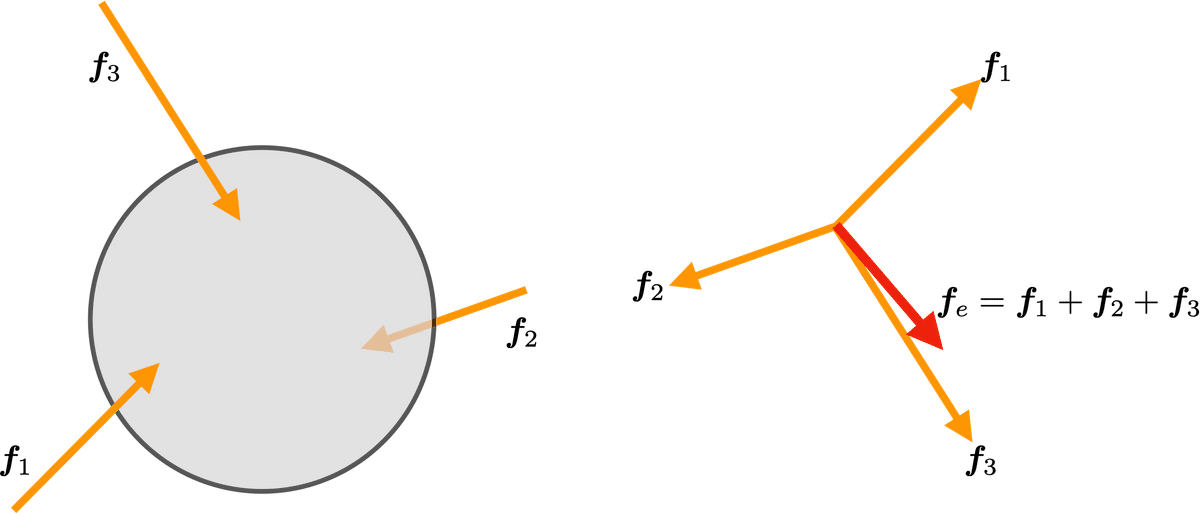
さらに図15のように,ロボットでは物体を3つ以上の力で把持をすることがあり,制御のために内力を定める必要がある場合もある.この場合も,ムーア・ペンローズの擬似逆行列で計算でき,筆者はこれが最も妥当な方法と考えているが,もはやそれが正しいかどうかという議論はできない.
補足2:身体各部の慣性モーメントモデル
慣性モーメントのモデルは,身体モデルの構成を強く拘束する.たとえば,これらの計算では各部位(セグメント,リンク)の両端の解剖学的特徴点が決められいる.ここで使用しているモデルは日本人の体格を意識して阿江ら(文献3)モデルを使用しているが,このモデルの構成は,必ずしも力学モデルを構成する上で適切な構成とはなっていない.モーションキャプチャで貼付するマーカの位置,すなわち解剖学的な特徴点との整合性もよくない.時代にあった新しい日本人の慣性モーメント,質量モデルが必要とされている.
補足3:ニュートン・オイラー法との整合性
このマガジン「動かして学ぶバイオメカニクス」の第14章
では,逐次的に計算して解くニュートン・オイラー法を用い,限定的・部分的にはなるが合成の運動方程式を与えた.ここでは,この延長で全身の運動方程式を計算し,それがこの章で示した全身の合成の回転の運動方程式と一致することを確認する.
運動方程式の左辺:
各部位$${j}$$の角運動量$${\bm{L}_j(O) = \bm{x}_{gj} \times \bm{P}_j + \mathcal{L}_j}$$の総和である全身の角運動量は
$$
\bm{L}(O) = \sum_{j=1}^n (\bm{x}_{gj} \times \bm{P}_j )+ \sum_{j=1}^n \mathcal{L}_j
$$
と書けるが,これを時間微分すると
$$
\dot{\bm{L}}(O) = \sum_{j=1}^n (\dot{\bm{x}}_{gj} \times \bm{P}_j + \bm{x}_{gj} \times \dot{\bm{P}}_j)+ \sum_{j=1}^n \frac{d \mathcal{L}_j}{dt}
$$
となる.ここで右辺第1項の$${\dot{\bm{x}}_{gj} \times \bm{P}_j}$$は,運動量の時間微分で述べた理由(同じベクトル同士の外積は零)と同じで
$$
\dot{\bm{x}}_{gj} \times \bm{P}_j = \dot{\bm{x}}_{gj} \times (m_j \dot{\bm{x}}_{gj}) = \bm{0}
$$
となり,また右辺第2項は第7章で導出したように
$$
\dot{\mathcal{L}_j} = \frac{d \mathcal{L}_j}{dt} = \frac{d (\bm{I}_j \bm{\omega}_j)}{dt} = \bm{I}_j \dot{\bm{\omega}}_j + \bm{\omega}_j \times (\bm{I}_j \bm{\omega}_j)
$$
となる.
そこで,この全身の角運動量の時間微分
$$
\dot{\bm{L}}(O) = \sum_{j=1}^n (\bm{x}_{gj} \times \dot{\bm{P}}_j) + \sum_{j=1}^n \dot{\mathcal{L}}_j
\\
= \sum_{j=1}^n (\bm{x}_{gj} \times (m_j \ddot{\bm{x}}_{gj}))+ \sum_{j=1}^n \dot{\mathcal{L}}_j
\\
= \sum_{j=1}^n m_j(\bm{x}_{gj} \times \ddot{\bm{x}}_{gj})+ \sum_{j=1}^n \dot{\mathcal{L}}_j
$$
を得る.
運動方程式の外力(右辺):
一方,合成の運動方程式$${\dot{\bm{L}}(O)}$$の外力は
$$
\dot{\bm{L}}(O) = \bm{x}_G \times M \bm{g} + \bm{N}(O)
$$
で記述されたが,右辺第1項は
$$
\bm{x}_G \times M \bm{g}
\\ = M \bm{x}_G \times \bm{g}
\\= M \frac{\sum_{j=1}^n m_j \bm{x}_{gj}}{M} \times \bm{g}
\\= (m_1 \bm{x}_{g1} + m_2 \bm{x}_{g2} + \cdots m_n \bm{x}_{gn}) \times \bm{g}
$$
であるので,これを代入し,
$$
\dot{\bm{L}}(O) = \sum_{j=1}^n m_j (\bm{x}_{gj} \times \bm{g}) + \bm{N}(O)
$$
と書き換えることができ,運動方程式の左辺と右辺を合わせ,
$$
\sum_{j=1}^n m_j(\bm{x}_{gj} \times \ddot{\bm{x}}_{gj})+ \sum_{j=1}^n \dot{\mathcal{L}}_j = \sum_{j=1}^n m_j (\bm{x}_{gj} \times \bm{g}) + \bm{N}(O)
$$
を得て,さらに,
$$
\sum_{j=1}^n m_j(\bm{x}_{gj} \times (\ddot{\bm{x}}_{gj} - \bm{g}))+ \sum_{j=1}^n \dot{\mathcal{L}}_j = \bm{N}(O)
\\
\sum_{j=1}^n m_j(\bm{x}_{gj} \times (\ddot{\bm{x}}_{gj} - \bm{g})) + \sum_{j=1}^n (\bm{I}_j \dot{\bm{\omega}}_j + \bm{\omega}_j \times (\bm{I}_j \bm{\omega}_j)) = \bm{N}(O)
$$
を最終的に得る.
ここでさらに,各部位に作用する慣性力と重力の和を
$$
\mathcal{F}_j
\stackrel{\mathrm{def}}{=}
\bm{x}_{gj} \times m_j(\ddot{\bm{x}}_{gj} - \bm{g})
$$
と定義すると,合成の回転の運動方程式は
$$
\sum_{j=1}^n (\bm{x}_{gj} \times m_j(\ddot{\bm{x}}_{gj} - \bm{g})) + \sum_{j=1}^n (\bm{I}_j \dot{\bm{\omega}}_j + \bm{\omega}_j \times (\bm{I}_j \bm{\omega}_j)) = \bm{N}(O)
\\
\sum_{j=1}^n (\bm{x}_{gj} \times \mathcal{F}_j) + \sum_{j=1}^n \dot{\mathcal{L}}_j = \bm{N}(O)
$$
と書き換えられる.

このことは図16が示すように,全身の運動方程式は,系内のすべての部位に関する,慣性力と重力の和$${\mathcal{F}_j = m_j(\ddot{\bm{x}}_{gj} - \bm{g})}$$の原点まわりのモーメントと,慣性力$${\dot{\mathcal{L}}_j = \bm{I}_j \dot{\bm{\omega}}_j + \bm{\omega}_j \times (\bm{I}_j \bm{\omega}_j)}$$を加算したもので記述できることを示している.
もし,系を全身の一部から切り出し,その切り出した境界の関節に作用するトルクを計算したい場合は,原点$${O}$$をその関節に設定すれば良い.それは第14章で述べた方法と一致する.
このように,第14章で述べたニュートン・オイラー法で算出した合成の運動方程式と同様に,慣性力項の加算と$${\sum_{j=1}^n \dot{\mathcal{L}}_j}$$,原点から見た各部位に作用する力の加算$${\sum_{j=1}^n (\bm{x}_{gj} \times \mathcal{F}_j)}$$で記述され,逐次的に計算される運動方程式と整合性があることが確認できた.
一見すると合成の運動方程式は複雑そうだが,
慣性力$${\dot{\mathcal{L}}_j = \bm{I}_j \dot{\bm{\omega}}_j + \bm{\omega}_j \times (\bm{I}_j \bm{\omega}_j)}$$
座標系の原点(好きなところに設定すればよい)からみた力のモーメント$${\bm{x}_{gj} \times \mathcal{F}_j = \bm{x}_{gj} \times m_j(\ddot{\bm{x}}_{gj} - \bm{g})}$$
の和となっている.もし単に数値的に解を得るだけが目的なら,いちいちこれらの角加速度や加速度を計算する必要もなく,これらの積分に相当する角運動量を構成する
慣性力$${\mathcal{L}_j = \bm{I}_j \bm{\omega}_j}$$
運動量ベクトルのモーメント$${\bm{x}_{gj} \times \bm{P}_j = \bm{x}_{gj} \times (m_j \dot{\bm{x}}_{gj})}$$
の和を数値微分するだけで,合成の回転の運動方程式の外力を計算する目的を達成できる.
しかし,重要なことは,これらは一見すると複雑な式に見えるが,図7,8,16に示されたように,座標の原点まわりの力のモーメントの加算など幾何学的意味が捉えやすい物理量である.単に数値的な大小ではなく,外積などの幾何学的意味がわかれば,運動から多くのことが直感的に理解できるはずである.
また,さらに何よりも重要なことは,第14章で述べたように,地面と接するような外部環境と相互作用する多くの場合,慣性力$${\dot{\mathcal{L}}_j}$$は外力と比較して小さく,関節に作用するトルクは外力との静力学的近似で記述できるということではないだろうか.
計算だけで量的な議論をするだけなく,これらの物理的な意味の直感的・幾何学的理解力を養っていただけたらと思う.
補足4:合成の角速度?
ここで,平行軸の定理により合成の角運動量$${\bm{L}}$$の計算を行った.またここでは示さなかったが,合成の慣性モーメント$${\hat{\bm{I}}}$$も平行軸の定理で計算可能だ.するとここで読者は疑問を抱かないだろうか?「合成の角速度$${\hat{\bm{\omega}}}$$というものは存在する?」
たとえば,フィギュアスケートのジャンプでは外力がほとんど作用しないので全身の角運動量が保存すると考えて良いだろう.そこで全身の合成の慣性モーメントも計算できるなら,全身の角速度も計算してみたくなるだろう.
これまでの理解から,ひとつだけ注意点に気がつくだろう.合成の角運動量$${\bm{L}(O)}$$も合成の慣性モーメント$${\hat{\bm{I}}(O)}$$も,それらは原点$${O}$$(回転の中心)に依存する可能性があるので,仮に合成の角速度が計算できたとしても,それは原点に依存した物理量になる可能性があるので注意が必要だ.この時点で普通の角速度とは異なり,違和感を感じる.
$$
\bm{L}(O) = \hat{\bm{I}}(O) \hat{\bm{\omega}}(O)
$$
から合成の角速度$${\hat{\bm{\omega}}(O)}$$を計算できる保証は,$${ \hat{\bm{I}}(O)}$$の逆行列$${ \hat{\bm{I}}^{-1}(O)}$$が存在する必要がある.通常の角速度を「運動学的角速度」とするならば,これに無理やり名前をつけるとすると$${\hat{\bm{\omega}}(O)}$$は「動力学的角速度」となる.逆行列が存在し計算可能なら,この合成の動力学的角速度 $${\hat{\bm{\omega}}(O)}$$を計算できそうだが,もちろんこれは物理の教科書にも出てこない.ロボットでも調査不足だがそのような概念はないのではないだろうか.この続きについては,またどこかで述べることとしよう.
なお,フィギュアスケートの全身の合成の角速度を計算する場合,たとえば身体重心まわりで合成の角速度を計算しても良さそうだが,その取扱は注意が必要だ.とくにそれを計算しなくてはいけない理由がない限りは,無理に動力学的角速度を計算するよりは,身体の軸を適当に定めて幾何学的に角速度を計算するほうが現実的ではないだろうか.
参考文献
1)梶田編著,ヒューマノイドロボット(改訂2版),オーム社,2020
2)内山,中村,ロボットモーション–岩波講座ロボット学2–,岩波書店,2004
3)阿江, 湯, 横井,日本人アスリートの身体部分慣性特性の推定,バイオメカニズム,Vol. 11, pp. 23--33, 1992



【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
【データの計測について】
スポーツセンシング社のスタジオで,フォースプレートやモーションキャプチャを利用した計測も行えます.出力されるデータと,ここで示したプログラム(入力データの取り込み関数を少々改変する必要があるが)で,同様な解析を行えますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
