グラフェンのエネルギー分散関係

折角なので物性の記事を。画像のサイズを均一にするのはこちら側でやらなければならないのだろうか？

序

強束縛模型でグラフェンのエネルギー分散関係を導出する。
グラフェンのフェルミエネルギー近傍では，pz軌道によるπ結合が支配的である。伝導などを考える際にはフェルミエネルギー近傍の状態を考えればよいので，pz軌道のみを取り入れた近似によって計算を進める。
ちなみに同じⅣ属(14族が適切かもしれない)元素は原子層を作ることが知られており，Siではシリセン，Geではゲルマネン，Snではスタネン，Pbではプランベンと呼ばれている。またⅣ属にとどまらず，ホウ素やリンも原子層を作る。グラフェン以外では，pzの１軌道のみを取る近似はあまり良くないらしい。また，バックリングがあるため軌道が混合する。さらに原子番号が大きくなるとスピン軌道相互作用が効いてくるので，それも取り入れる必要がある。

結晶構造

グラフェンはハニカム格子(ハチの巣格子，正六角形)を取っており，これがグラフェンの特異な現象を引き起こす原因になっている。この格子は3回回転対称性(120°回転で不変)を有している。格子ベクトルは

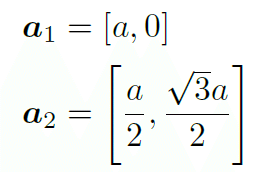
であり，図のa1,a2と対応している。

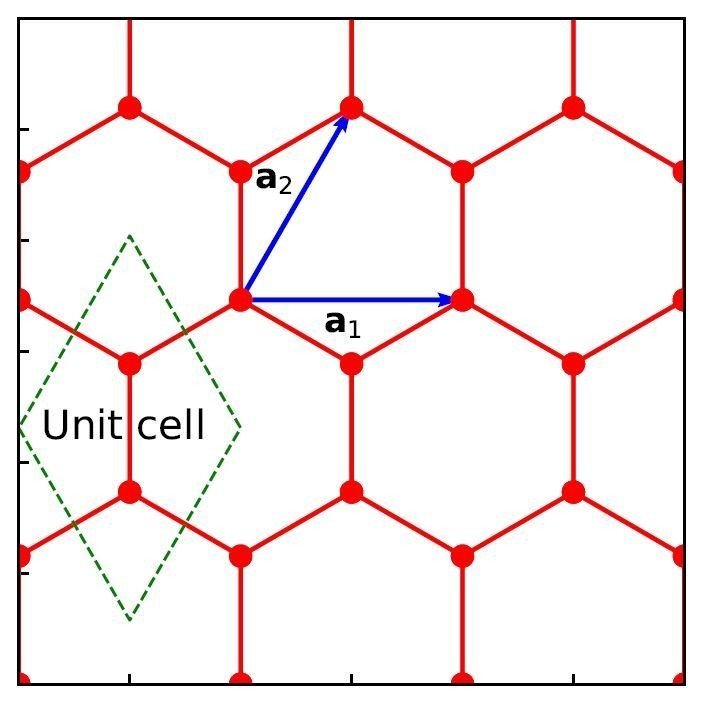
単位胞は好きにとって良いが，今回は図中の緑の破線で囲われた領域を単位胞とする。単位胞には原子が二つあるので，それぞれをAサイト，Bサイトと呼ぶことにする。AサイトとBサイトの間は，どのように基本並進ベクトルを組み合わせても移動することはできない。したがって非等価な点となっている。ここでAサイトとBサイトを結ぶベクトルを

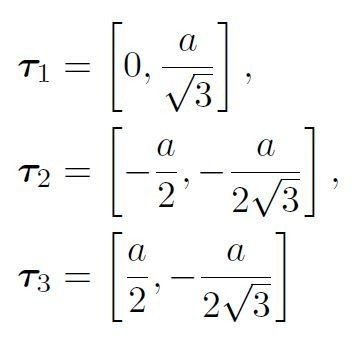
としておく。ちなみにAサイトかBサイトかのように2価的なものは数学的にスピンと同様の構造と見なすことができるので，これを擬スピン(pseud-spin)と呼ぶ。

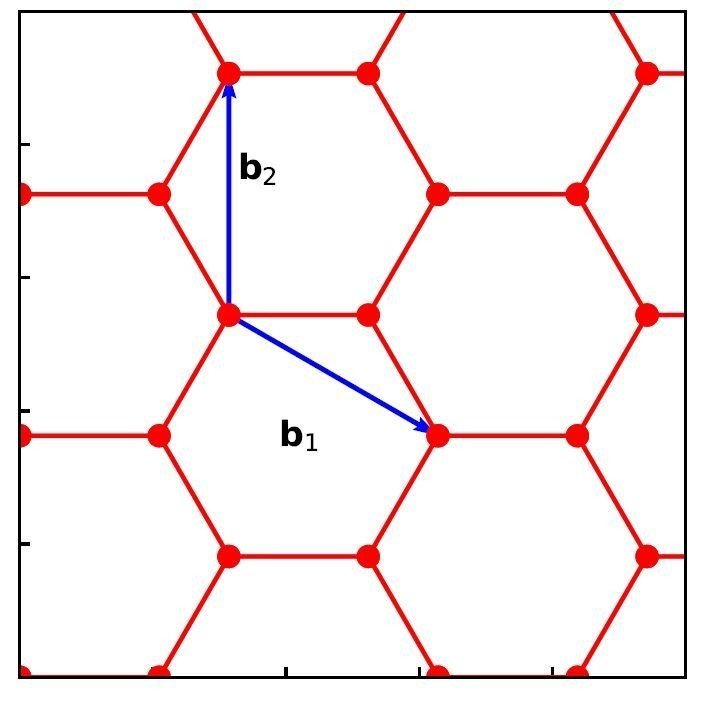
今度は波数空間を考える。波数空間での基本並進ベクトルは

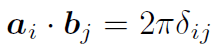
から求めることができて，

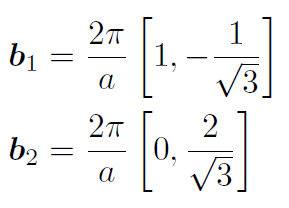
となる。一つ上の図にそれを図示した。

基本並進ベクトルはこのように選ばなくてもよい。仮に実空間の基本並進ベクトルa1,a2をなす角が120°となるように選ぶと，波数空間ではなす角が60°の基本並進ベクトルb1,b2が得られる。文献によってはこちらの選択をしているものもあるので気をつけなければならない。

Tight-binding近似

今回は最近接の飛び移り積分のみを考慮したTight-binding近似を適用する。波動関数をAサイトとBサイトの重ね合わせで

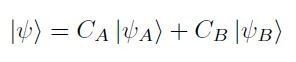
とする。このとき

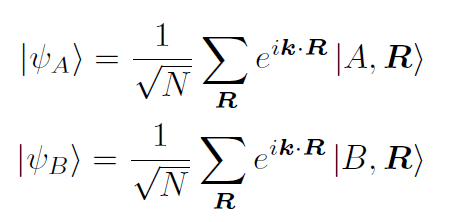
で，互いに直交していると仮定する。1/√Nは規格化定数，ベクトルkは波数ベクトル，ベクトルRはサイトの位置ベクトルである。Schrödinger方程式は

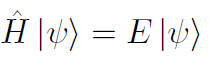
である。こちらに＜ψA|,＜ψB|を作用することで，以下の行列表示が得られる。このときオンサイトエネルギーをエネルギー原点に取った（対角成分を0とおいた）。

２行目の式は飛び移り積分から生じる項で，今回の近似では最近接の飛び移りのみを考慮するので，このようになる。γ0は飛び移り積分である。計算過程は以下の通り。γ0は方向によらない。

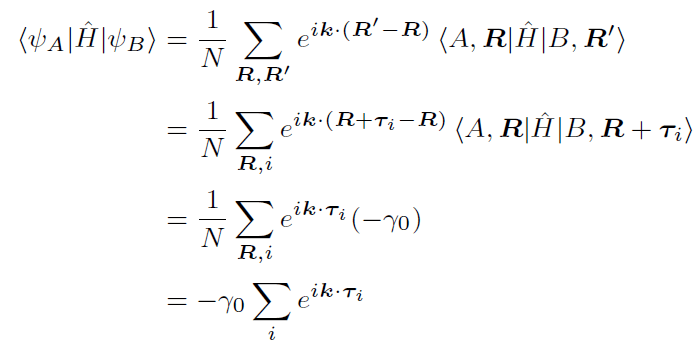
分散関係

あとは固有値方程式det[H-EI]=0を解けばよいので，

となる。これを以下にプロットする。

K,M,Γは波数空間の対称点である。

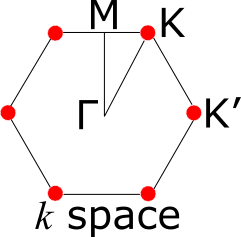
3次元的に見栄えよくプロットしたのが上図である。しかし，見栄えが良いだけで得られる情報が少ないので個人的にはあまり好きでない。しかも本来は伝導体と価電子帯がK点で接しているはずである。今回はメモリ不足で格子点をそこまで細かく取ることができなかった。

Ｋ点付近

最後にK点まわりで展開してみる。まずK点の座標は

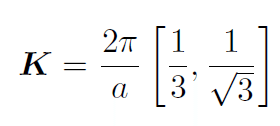
である。k=K+qとして，|q|aで先程の分散関係Eを展開すると，

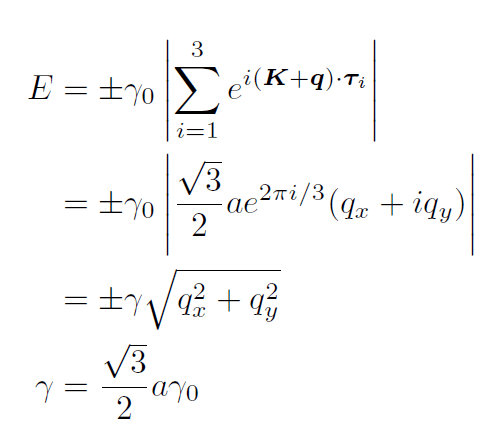
が得られる。この結果，K点まわりでは波数の大きさに比例することがわかる。すなわち等方的である。

しかし，Ｋ点から離れると異方性が現れて，それがまた面白い現象を引き起こすこともある。

まとめ

今回はグラフェンの分散関係をTight-binding近似の下で計算した。その結果K点付近ではバンドが線形分散を持ち，伝導体と価電子帯が接することがわかった。本文中では述べなかったが，K’点も同様である。さらに進んで有効質量近似まで考えると，Dirac方程式の話と関連して面白い。

参考文献

T.Ando, Journal of the Physical Society of Japan, 74, 777-817 (2005)