【素数筆算】素数を重ねて素数を作ろう(ひきざん編)

昨日、「素数筆算」と題して、新しい素数を作ろうという記事を投稿しました。

今回は「ひきざん編」です。素数同士で筆算によるひきざんをするわけですが、どんな感じで計算するかを最初に説明します。

たしざん編で素数をずらして足したように、ひきざんでも素数ずらして引きます。

2つの素数である2と3を使い、「3−2」を行う場合は、大きい3の方を1桁左にずらします。つまり、30−2という計算になるのです。

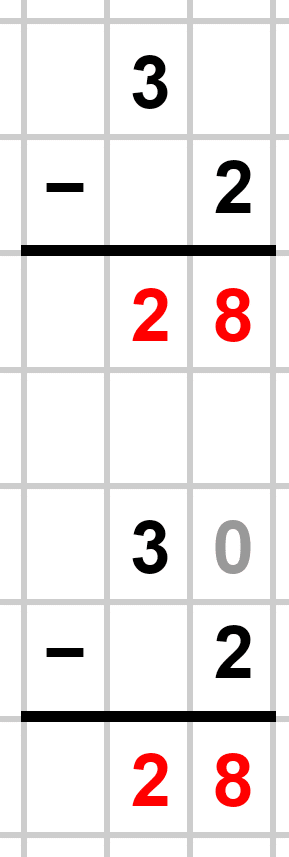
色々な素数で試すと切りがないので、今回は「双子素数」の2つの素数を使ったひきざんを紹介します。果たしてどれくらい素数が登場するのか…！？

最初に100以下の双子素数のケースを載せていきます。赤数字が素数、青数字が合成数で、素因数分解も合わせて表記しています。

意外と素数率は高いでしょうか…！？実はもっと大きな数になると、そうでもありません。

とはいえ、難しい素因数分解ばかりが登場するので、作成していた筆者はワクワクしてしまいました…！😆

以下に1000以下の双子素数のケースをすべて載せます。ちなみに、1000以下の双子素数は全部で35組あるのです。

さらにちなみにですが、700台と900台の双子素数は全くないようです。知りませんでした。1000以下の最大の双子素数は(881, 883)です。

それではどうぞ！

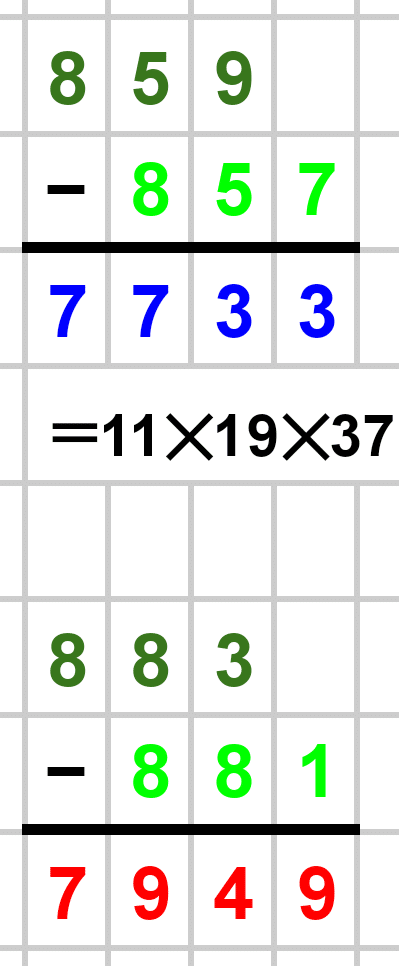
いかがでしたか？

素数もある一方で、すぐには素因数分解できない合成数たちもたくさん登場していましたね。

ちなみに、3の倍数は全く登場しませんでした。これは以下のように説明できます。

p, p+2を双子素数としたとき、

『p+2』と『p』の素数筆算によるひきざんは、

(p+2) × 10 − p = 9p + 20 = 9(p+2) + 2

つまり、3で割った余りは2になるので、3の倍数にはならないのです。

さて、このnoteでは何度も宣伝していますが、素因数分解を使った以下のゲームを楽しんでいます。

4桁の素因数分解は結構難しいので、今回の筆算で登場した素因数分解たちは覚えておきたいものです。筆者自身は、このnoteを何度も見返そうと思います。

素数と素数を組み合わせると、新しい素数ができる。素数界の『化学反応』をこれからも考えていきたい。

(迷言…？)

素数はいつも、あなたのそばに。
Let's enjoy SOSU !

最後まで読んでいただき、ありがとうございました。