至る所微分不可能な連続関数「高木関数」
1901年、日本の代表的な数学者の一人、高木貞治先生が、至る所微分不可能な連続関数を発表されました。それは次のように表される関数です。
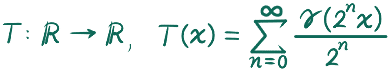
ここで γ は

という関数です。
この関数 T は連続関数であるにもかかわらず、微分可能な点が全く無いという奇妙な関数です。今は高木関数(Takagi function)や高木曲線(Takagi curve)などと呼ばれています。
ちなみに、至る所微分不可能な連続関数として最初に発見されたのは1872年の Weierstrass 関数ですが、この記事では、形がよりシンプルな高木関数について見て行きたいと思います。
なお、この記事は次の動画のダイジェスト版のような位置づけとして書いています。
動画を見るのはかったるいし俗っぽいのは嫌という方は note で、じっくり説明してほしいという方は動画でご覧いただければと思います。
いや、まあ、この記事が俗っぽくないかと言われればそんなことはないかもですけどゴニョゴニョ...
高木関数ってどんな形?
まず、関数 γ について見てみましょう。

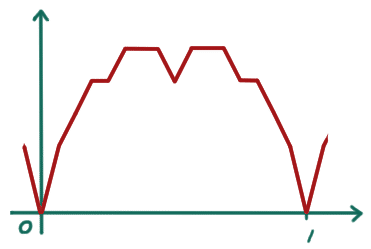
γ は、与えられた実数に対し、その実数からその実数に一番近い整数までの距離を返す関数です。例えば γ(0.7) = |0.7-1| = 0.3 です。グラフにすると次のような形です。

ギザギザですね。三角波関数と呼ばれるそうです。微分不可能な点が均等に分布していますが、微分可能な点はまだまだたくさんあります。
さて、問題の高木関数

はどんな関数でしょうか。
Σ の中身の関数を見てみましょう。n が 0 のときは γ(x) そのものですね。グラフはさっきと同じく、次のような形です。

n が 1 のときのグラフはどんな形になっているでしょうか? そう、γ のグラフを、原点を中心に横方向と縦方向の両方向に半分に縮小したグラフですね。つまり、

こんなグラフです。
n が 2 のときは――同じですね。n が 1 のときのグラフをさらに半分に縮小したグラフです。

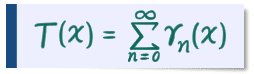
こんな風に、半分に縮小したものを足して、半分に縮小したものを足して、という操作を無限回繰り返して作られるのが高木関数です。つまり、

これが

こうなって、

こうなって、
こうなって、っていうのを繰り返していくわけです。どんどん微分不可能点が増えてますね。最終的には

こんな形で、もこもこしてます。ブラマンジェという洋菓子に形が似ているということで、ブラマンジェ曲線(blancmange curve)とも呼ばれるそうです。
高木関数の連続性
三角波関数やそれを何度か半分に縮小した関数は連続ですが、連続関数の無限和が連続関数になるとは限りません。しかし、一様収束していれば話は別です。

ということで、

さて、これをどうやってチェックしましょうか? 直接チェックするのはちょっと大変そうですね。でも、級数の一様収束性をチェックする便利な道具があります。

Weierstrass の M テストを使えば、Σ の中身に絶対値を付けて上限を取ったものの無限和の有限性を調べるだけで、一様収束性が言えるのです。
γ の絶対値の上限は 1/2 ですね。ということは

ですね! 一様収束性が言えて、高木関数の連続性が帰結できました。
高木関数が至る所微分不可能であること
※以下、Billingsley によって1982年に発表された簡潔な証明のアイデアを参考にしています(P. Billingsley. Van der Waerden's Continuous Nowhere Differentiable Function. The American Mathematical Monthly 89.9 (1982): 691-691)
目標はこれですね。

「無限和引く無限和を含む極限とかどう考えたらいいの?」と思われるかもしれませんが、T(x) は x の値ごとに、無限和になったり有限和になったりするんです。ということで、

有限和になるところを調べてみましょう!

再掲。
ちょっと式がうっとうしいので

と置きますね。つまり
となります。これが有限和になる x とは? まず

ですね。ということは

で有限和ですね。(2^k)x が整数なら (2^(k+1))x も整数だし、(2^(k+2))x も整数だし、以下略。
ちなみに、(2^k)x が整数になるっていうのは 2 進数表記で有限小数になるってことですね。こんな実数 x に対しては T(x) は有限和です。有限和ならいろいろ調べられそうですね。
試しに、2/8 と 3/8 を使って、例を見てみましょう。T(2/8) も T(3/8) も、γ_3 以降の項は消滅するので、

というように計算できますね。グラフの傾きに着目すると、いずれの項も 1 か -1 のどちらかです。もちろん γ_3 以降の傾きはすべて 0 です。
この観察に基づいて一般の場合を調べると、次のことがわかります。

T が有限和になる点で調べると、結構すっきりした事実が見えてきましたね。
とはいえ、欲しいのは任意の実数 x に対する微分係数。ということで、以下実数 x を任意に取って固定して、x を近似しましょう。

つまり

を満たす数列 a_k, b_k として、

としましょう。すると、先ほど得た事実により、傾き
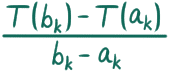
は、1 か -1 をちょうど k 回足した値になりますね。ということは

ですね。1 や -1 という奇数を奇数回足せば奇数だし、奇数を偶数回足せば偶数ですから。
はい。さて、奇数番目で奇数、偶数番目で偶数を取るような整数列は収束するでしょうか? もちろん

ですね。x を近似する二つの数列による傾きが、近似をいくら細かくしても収束しない。こんなの、もう、どうしたって微分不可能ですよね。
細かいところを詰めていきましょう。背理法を使うと楽ですかね。

すると、b_k は x とは異なる値を取りながら x に収束していくので、y のところを b_k に変えて k → ∞ とすると

となりますね。あ、分母分子の - の前後入れ替えてます。
a_k についても同じことをしたいんですが、a_k = x となる可能性があることを考えると、場合分けした方がいいですかね。
(i) x が 2 を何回か掛けて整数になるようなケースでは、数列 {a_k}_k が途中から x と一致するので、さっきの

から

が出てきて、矛盾。
(ii) x が 2 を何回掛けても整数にならないようなケースでは、a_k と x は常に異なるので、

ですね。これと、さっきの

を合わせると、

が言える気がしませんか? 次の補題を見ましょう。

ということで、

となり、矛盾が導けました!
おまけ




―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―
【爽籟 蜜柑(そうらい みかん)】
数学記事書いてる人。→ ブログ
Youtube チャンネル ↓
―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―・―