【スマホでPython数学】 第4章 関数のグラフ(plot命令)と方程式の解
学校では関数と方程式を別々に学んで、連立方程式や微分・積分で、急に関数のグラフが出てきます。関数のグラフを描くのは、ある程度数学の知識がないと描けないので、そのような順番なのだと思いますが、Pythonでは簡単にグラフが描けます。そこで、この章では関数のグラフと方程式の解について、Pythonを使って理解したいと思います。
1.関数のグラフ:plot(プロット)命令
まず、二次関数のグラフを描いてみます。
Sympyでは、非常に簡単に関数のグラフを描くことができます。
それでは以下のように入力してみてください。最初の2行はいつものおまじない(Sympyモジュールの呼び出しと、関数($${x}$$)の定義)になります。$${x^2 -4x -5}$$の関数のグラフはどうなるでしょうか?
from sympy import *
var('x')
plot(x**2 -4*x -5)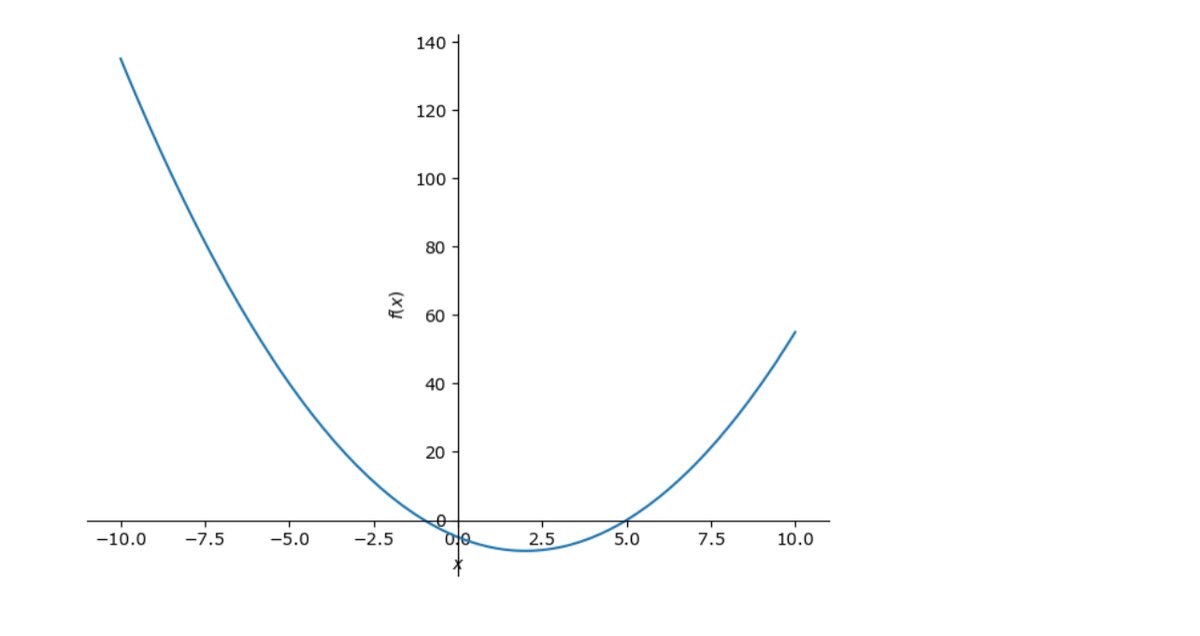
こんな感じのグラフになったでしょうか?
予め注意していただきたいのは、縦の軸($${f(x)}$$)と横の軸($${x}$$)のメモリ(スケール)が同じではありません。ここでは、グラフと横の軸($${x}$$軸)の関係(交点)が分かれば良いだけなので、このグラフでも良し、としてください。
plot命令を使うだけで、簡単にグラフが描けるので、感動しませんか!?
2.x軸との交点を強調する
$${x^2 -4x -5}$$の関数は、因数分解するとどうなるでしょうか?
これまでの章の学習からfactor命令を使って、$${(x + 1)(x - 5)}$$と因数分解できることが分かります。
このことから、以下の3つのことが分かります。
$${x^2 -4x -5 = 0 }$$の解は$${x=-1, 5}$$である
$${x^2 -4x -5}$$の関数は、x軸と$${x=-1, 5}$$で交わる
$${y=x^2 -4x -5}$$のグラフの軸は$${x=-1, 5}$$の中間点である$${x=2}$$になる
Sympyモジュールにあるplot命令では、グラフの描画範囲を以下のように指定出来ます。
plot(x**2 -4*x -5, (x, -2, 6))plot( )の左が関数、右にある「(x, -2, 6)」の部分が、xの値の範囲を-2〜6で表示してください、という意味になっています。
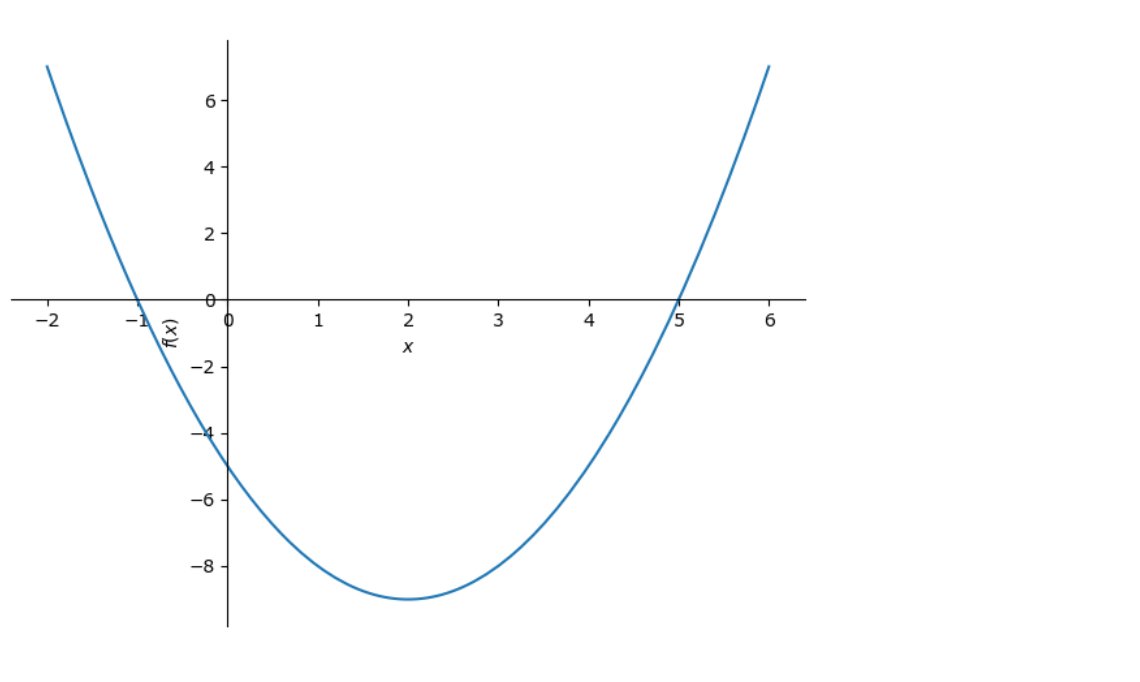
どうでしょうか?
下に凸の放物線(二次関数のグラフのことを放物線と呼びます)がx軸と-1、5で交叉しているのが分かります。これが方程式$${x^2 -4x -5 = 0 }$$の解になります。グラフから分かるのは、2つの関数のグラフ、直線$${x = 0 }$$と放物線$${y = x^2 -4x -5}$$の交点がこの2つの方程式の連立方程式の解でもあると言うことです。
また、放物線は左右対称性にできていますので、線対称の軸というのがあります。この軸は2つの交点$${x=-1, 5}$$の中間点である$${x=2}$$であることが分かります。グラフから$${x=2}$$で左右対称であることを確認してください。
3.高次関数のグラフ
二次関数のグラフは分かりやすいですが、とても大切です。特に、軸と頂点という項目については、教科書などで確認しておくことをお薦めします。他の章でも放物線のグラフについて再度登場することになると思います。
ここでは三次関数などの高次関数のグラフを描いてみましょう。
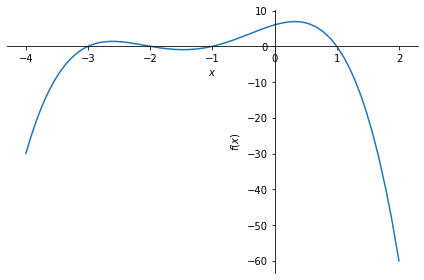
$${y = x^4 - 3x^3 - 4x^2 + 12x}$$
from sympy import *
var('x')
plot(x**4 -3*x**3 -4*x**2 + 12*x, (x, -3, 4))x軸との交点に着目してください。
$${x = -2, 0, 2, 3}$$で曲線とx軸が交叉しています。$${x^4 - 3x^3 - 4x^2 + 12x}$$の関数を因数分解できますでしょうか?
factor(x**4 -3*x**3 -4*x**2 + 12*x)コピペで簡単にできますよね。factor命令で簡単です。
$${(x+2)x(x-2)(x-3)}$$となります。これは$${(x+2)x(x-2)(x-3)=0}$$とした時の答えとX軸との交点が一致します。
もう一つ、高次関数グラフの形の原則についてお話します。
まず、一番次数の大きな変数の係数が「プラスかマイナス」かを見ます。プラスの場合は、必ずグラフが右肩上がりになります。マイナスの時は、グラフは右肩下がりになります。以下の図を見て比べてください。
例:$${y=x^3-4x}$$は右肩上がり、$${y=-x^3+4x}$$は右肩下がり
次に、これは「基本的に」という前置きがありますが、放物線のような「コブ」が二次関数だと1つ、三次関数だと2つ、四次関数だと3つ…、となります。以下、演習で関数のグラフを書いてみてください。ちなみに一次関数は直線になるので、「コブ」はありません。
4.演習
演習1:$${y = 2x+3}$$
演習2:$${y= -x^2-x+2}$$
演習3:$${y= -x^4-5x^3+5x^2+5x+6}$$
まとめ
やっと、コンピュータを使った方が簡単そう、という段階になってきました。次の章では「関数」と「方程式」について勉強したいと思います。
解答
演習1:$${y = 2x+3}$$
plot(2*x + 3, (x, -3, 2))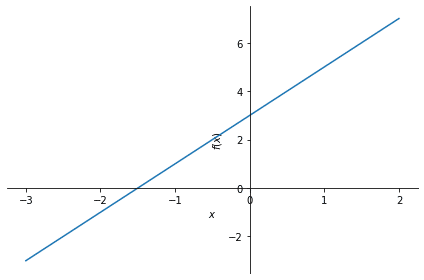
演習2:$${y= -x^2-x+2}$$
plot(-x**2 -x +2, (x, -3, 2))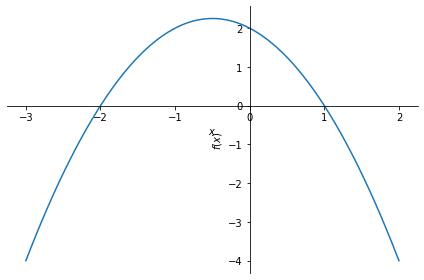
演習3:$${y= -x^4-5x^3+5x^2+5x+6}$$
plot(-x**4-5*x**3+5*x**2+5*x+6,(x,-4,2))