【中学校の数学の知識でユークリッド原論＃001】命題１．与えられた線分上に正三角形をつくること（作図）【第1巻】

数学が面白くないのに数学を教える苦しさ

大きな声で言えないのですが、もう何年も算数や数学を教えているのですが、いまだに算数、数学の楽しさが分からないです。

学生の時から解けるのは嬉しいのは分かるのですが、好きな教科でもなければ、どちらかというと嫌いで苦手な教科でした。

どうしても、好きになる要素が見つけることができませんでした。

ちなみに、理系の数学嫌いは進める道が限られてしまうのでおススメしないです。

科学者の中には数学が苦手な科学者は何人もいるのですが、現在は科学者で数学が出来ない人はほとんどいないのではないかと思うくらい、科学と数学は密接にかかわっていますね。

しかし、何年も勉強したり、教えたりしているのですが、できない問題が出来たことで以外で楽しいと思えることがほぼないです。

つまり、私は数学という学問の楽しさをまだ知らないということなんですよね。

実はずっとこのことがコンプレックスになっていて、数学の本当の楽しさを知らないのに教えていていいのだろうかということが常に頭にありました。

しかしながら、数学の楽しさを学ぶには何が必要なのかが分からないんですよね……。

そして数年の月日が流れ……、昨年のことになるのですがユークリッド原論という本を衝動的に買ってしまいました。

なぜ買ったかというと、科学者の人生を調べているときに、何人かの科学者が学生時代にユークリッド原論を学んでいたからという、ミーハー気分で買ってしまいました。

現時点では命題26くらいやったのですが、これが今まで数学で感じたことがない面白さがありました。

この記事のシリーズは、私がユークリッド原論を勉強することで数学の楽しさに気付くことができるかどうかの軌跡になります。

現時点ではちょっと楽しいかもと思い始めてきて、週６命題を目標に勉強しています。

ちなみに、もう何年も高校数学以降の勉強はしていないので、私の学力は中学数学レベルだと思ってください。

そんな私が、中学数学レベルの頭で、学んだユークリッド原論の内容を解説していきながら、数学の楽しさを分かることができるようになるかを赤裸々に書いていく記事になります。

まぁ、ユークリッド原論の旅はとてつもなく長いのでのんびり歩んでいこうと思うのですが、これで数学楽しかったと思うのもいいですが、これで数学が楽しくなかったと思ったとしてもいいと思っています。

何もしないで、知ろうとしないで、嫌いなるのは何か違うのかなっと思うので、いったん数学という学問と向き合ってみようと思います。

ユークリッド原論を知っている人は分かると思いますが、とても、とても長い旅になるので、何年かかるかは分かりませんが、たまに見に来てもらえると嬉しいです。

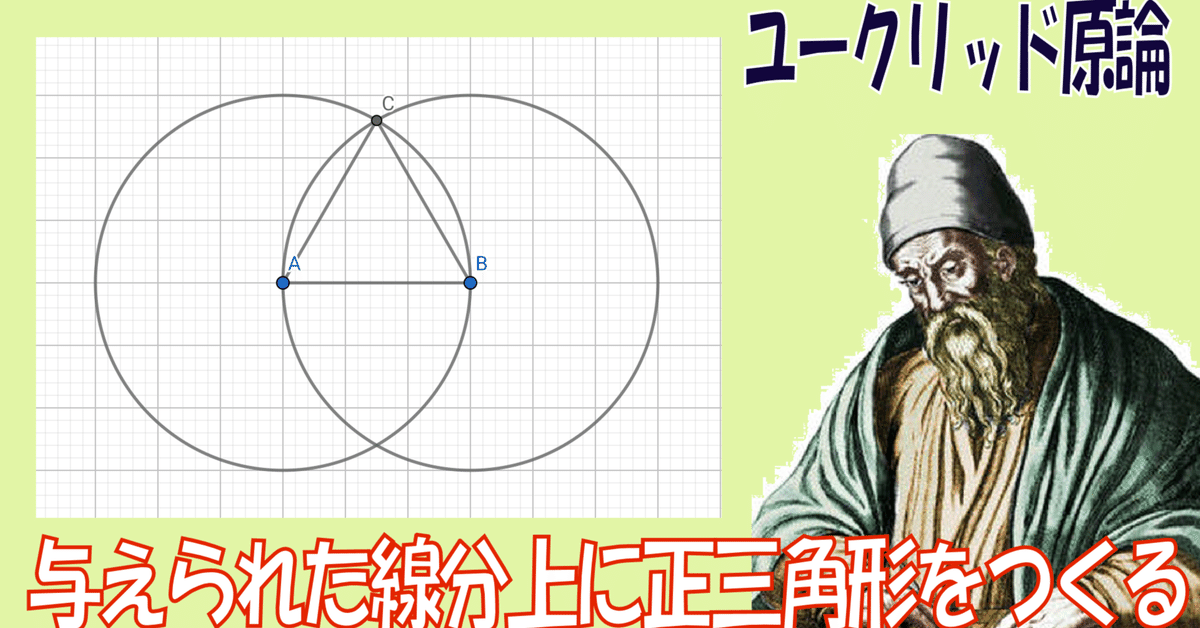
命題１.与えられた線分上に正三角形をつくること

線分ABがあります。
このとき、線分AB上に正三角形を作図しなさい。

まずは、線分ABを半径、中心を点Aとして円を描きます。

次に、線分ABを半径、中心を点Bとして円を描きます。  

円Aと円Bの交点を点Cとします。
そして、点Aと点C、点Bと点Cを結びます。

円Aの半径なので、
AC＝AB　・・・①
となります。

円Bの半径なので、
AB＝BC　・・・②
となります。

①と②にはABが共通なので、まとめてあげると
AC=AB=BC
となります。

したがって、AC、AB、BCの３つのすべての辺は等しくなるので、
三角形ABCは正三角形になります。

これで、線分AB上に正三角形を作図することができます。