三角関数を説明する(1) ~ギリギリ嘘をつかず最短手で説明したい編~
このシリーズの目的
初めまして、"木星のそばや"と申します!
自己紹介
昔、とある東大専門進学塾で、数学講師やってたよ!
今は、CGの会社で、数学的サポートするお仕事だよ!
ここでは
【なるべく早く】
【ギリギリ嘘をつかずに】
【ほとんど日常的な算数しか使わずに】
三角関数とは何か?を、伝えようとする""個人的な試み""です。
今日やること
今日は、突然いきなり「サイン・コサインってどういう意味?」に真正面から答えていきます。5分後には終わっています。
5分後には、あなたも「サイン・コサインを他人に説明レベル」に既に達しています。凄くないですか…!?
まあ、見ていきましょう。
(混乱をきたすので、高校生以下の人はこの記事読まないでほしいです!)
「サイン・コサインって何?」本編
[1/8 節] xy平面の復習
今日の話のスタートは「xy平面を、なんとなく分かろう」です。
地図でも表でも、平面的に整列してるものは、大体 xy平面 に似ています。
あの、まあまあ、とにかく画像を見て下さい。

右方向が x、上方向が y ということにしましょう。
例えば、図のオレンジ色
【ゼロ地点から、右に2・上に3、進んだ場所は、座標(2,3)である】
と言ってるだけです。
x, y で、点の場所を説明します。住所のようなものですね!
強いて言うなら、左方向や下方向はマイナスであることに注意してください。
例えば緑色は
「左に2.5, 下に1」進んだ点は、座標(-2.5, -1) といった具合です。
いかがですかね…? そんなに難しいでしょうか…?
以上を何となく分かれば、xy平面は、もう一旦十分です。
[2/8 節] xy平面に円を描こう
この、xy 平面に、直線でも折れ線グラフでもなく、なんと、円を描きます。
それもド真ん中に、です。
唐突ですが、「半径1の円」をド真ん中に置いてみても宜しいでしょうか。

真ん中のゼロ地点(原点, といいます) を中心に半径が1ですから、画像のようになります。
例えば、円の右端は(1, 0)・下端は(0, -1)なのが、図から分かりますね、
もっと言えば「x座標 -1~1、y座標 -1~1、に、すっぽりと収まっている」とも言えそうです。
どうでしょう。
でも手順としては、これで既に半分まで来ましたからね。次に進みます。
[3/8 節] 円周上で、角度を数えよう
円の右端、つまり点(1,0)から、反時計回りに回っていく人を想像します。
図の通りです。一目瞭然ですね。
やがて90°に達し、順に180°・270°地点を走破し、360°回ったら、それはもちろん「1周した」ということです。
円上では「0°の点」と「360°の点」は同じ右端を指します。

45°地点と言ったら…? 右上ですよね。
270°地点と言ったら…? 円の下端となります。
その確認ができれば、十分OKです!
[4/8 節] 「好きな角度を、円周上にとる」
ここが今日の唯一にして最大の難関なのかな?と思います。
見出しの通り、円周の上に、適当な角度をとります。
何度でも良いのですが、今回は40°で、やってみますね。
円周上の、40°地点とは…? どこだ?
前節に登場した「円周上を走る人」を思い出して。

そこです。
そこですよ。

図では緑色のお星さまを付けましたが、
「反時計まわりに」「右端から」で、40°、とってください。
その点を注目し続けて下さいね。
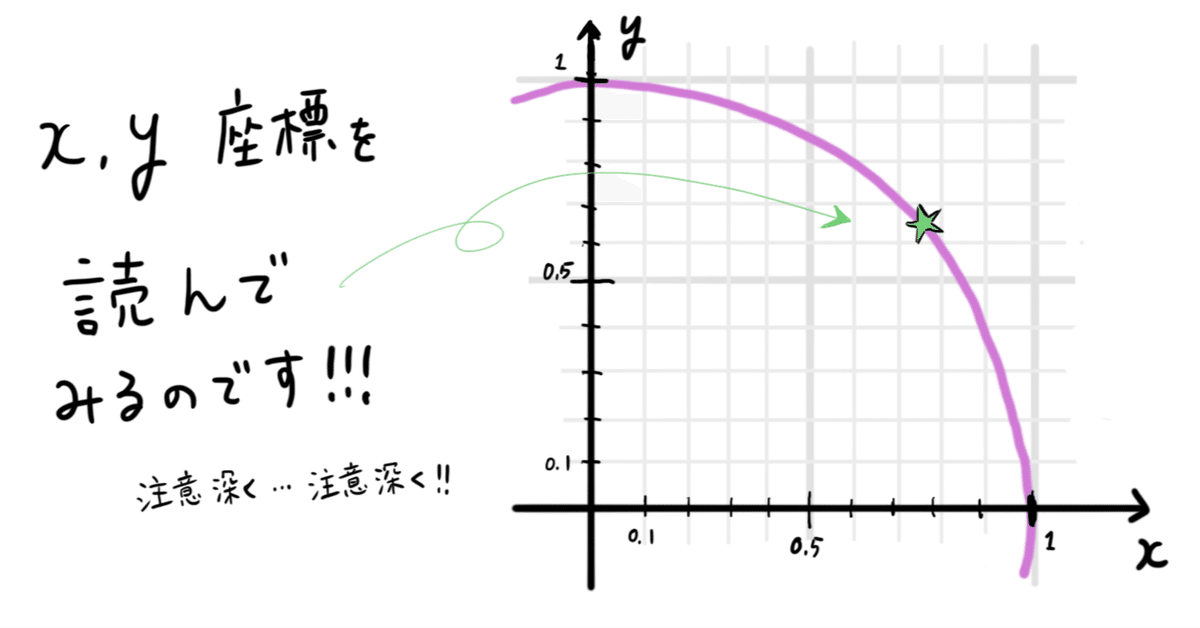
[5/8 節] その座標を読む
では、その点の「座標」を、読んでいただくこと、できますでしょうか。
ヒントとしては、x も y も、1よりは明らかに小さいですよね。
どうです? いくつくらいに見えますか・・・?

・・・。
・・・・・・・・・。
どうでしょうか。

実は、頑張って測ると、0.766, 0.642 ”くらい”、になるのだそうです
(物好きな人は、細かい目盛りの入った方眼用紙に、円を描いて、測ってみて下さい。実際こういう値になります。)
[6/8 節] サイン・コサインとは??? 衝撃の結末!!
さあ。
「円周上の40°の点」の x, y 座標は、0.766, 0.642 ”くらい”、でした。
これをそれぞれ、cos40°・sin40°、と、呼ぶことにしましょう!
つまり、こうです。

cos はコサイン・sinはサインと呼びます。
そうです。
実は、これが、サイン・コサインの正体なのです…!! (どうです…?)

どうでしたか?
数学の難しい概念の象徴、として
「サイン・コサイン」が語られることだってありますが、
それが、こんなに単純な手続きで説明されることに、
驚かなかったでしょうか…?
が、ピンとこない方も多いと思います
ので、具体例を色々観察して、情緒を味わってみましょう。
[7/8 頁] 具体例
例えば、40°じゃなく、90°の場合を考えてみましょうね。
考える「円上の点」は、図の位置です。

【右端からスタートして】
【そこから反時計回りに】90°の地点… ですから?
90°と言ったら、ここになるわけですね
この「右端からスタート」「反時計回り」はとても重要で、
ここは覚えてもらう必要があります・・・。
それで、その点の
・x 座標が cos90°
・y 座標が sin90°
なわけですから・・・どうですか?

90°地点は、きれいに座標は(0, 1)ですよね。
なので、その x 座標・y 座標が、cos90°・sin90°ですから、
cos90° = 0
sin90° = 1
ということになります。
さて
例えば今度は、180°の場合も全く同様です。
「cos180°・sin180°はいくら?」と聞かれたとしましょう。
やはりまずは、「180°地点とは、どこか?」を考えるわけです。
同じように【右端からスタート】して、【反時計回りに】180°を辿ると…
この点に来ませんか?

もう大丈夫ですね。
「円上に角度をとり、座標を読む」
この一言に尽きます!!
ただ「右端スタート」「反時計回りに」というのが何気に重要です。
それでcos, sinが出てきます。
※
<<こちら>> に練習問題を4つ用意してみました。解説つきです
「どうしても、練習をこなして慣れたい」という人のみ、どうぞ!
[8/8 頁] おわりに
確認問題を1つ置いて、今回は終わりとします
・cos270° と sin270° は、いくらでしょうか?(答は記事最後)
これに正解できれば、「サイン・コサインの意味」に関しては、
最低限、理解できたことになってしまいます。
しかし、よく考えると、疑問はまだまだ残るかもしれません。
・そういや、タンジェントって奴も居なかった?
・「サイン・コサインとは、波である」とよく聞くけど、どういうこと?
・プログラミングでどう使うの?CGでは?
・図形問題とか建築に、応用できるんじゃなかったっけ?
・サインコサインなんて、結局、何の役に立つの?
残念ながらこの辺りへの回答は、今回の「sin/cosの意味」よりも、数段難しくなります。
が、今回のように丁寧に追いかけていけば、説明は案外可能です。
次のセクション以降で説明することとしましょう!
次は、三角関数の第2章、「弧度法」をお届けしたいです。
確認問題の答え
cos 270° = 0
sin 270° = -1
【説明】

「右端から」「反時計回り」を忘れないでくださいね、
右端から、270°回ってくると、円の下側に辿り着きます
座標を読むと (0, -1) だと思いませんか…?
その x 座標が cos 270°、y 座標が sin 270° だというわけです
ということで、cos270° = 0, sin270° = -1 と分かります!
