
2022年九大理系数学[1]
今回は2022年九大理系数学[1]を解説します。
問題はこちら。

2022年のセットの中で、唯一手がつきやすかった問題ですね。これは落とせない問題となりました。目新しい点もなく、標準問題の典型だったかなと思います。
(1)は問題文にあるように、
・ベクトルnは、ベクトルaとベクトルbに垂直である→内積ゼロ
・ベクトルnは、大きさが1
から3つの未知数を設定して解いていけばいいでしょう。
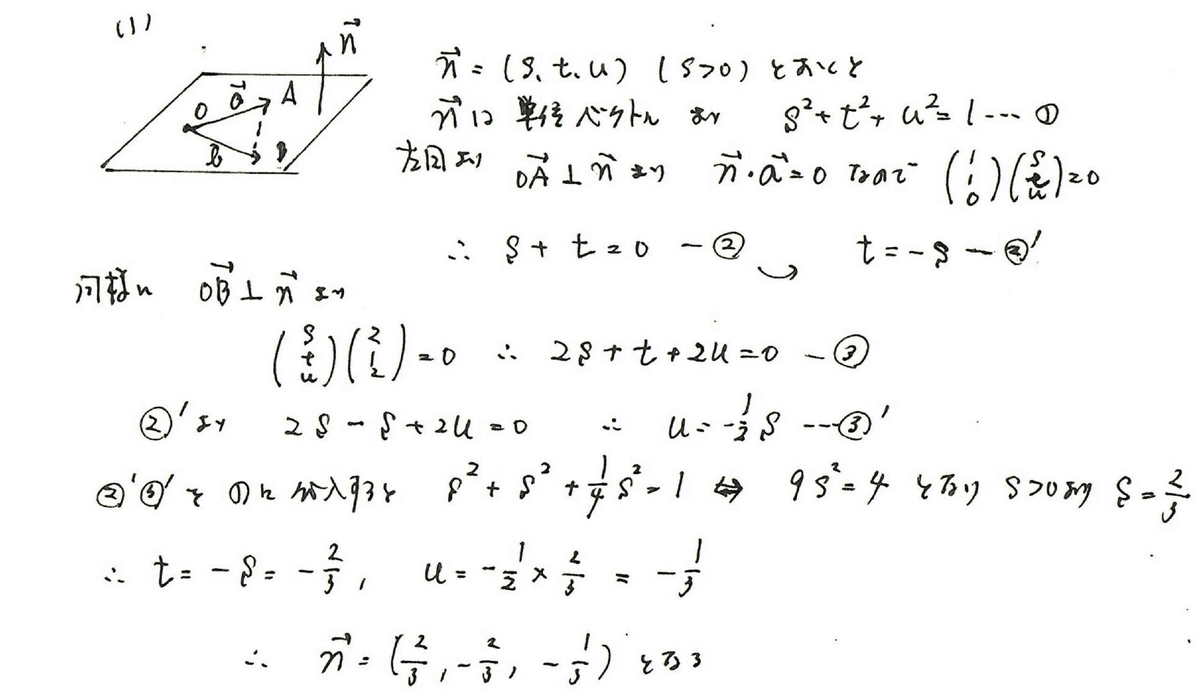
(2)は平面αに対して対称な点を求めます。図示して関係性を見つけていきます。
図形と方程式で扱う対称な点の問題と同様に中点を意識したいですね。
ベクトルpp’はベクトルn(平面αの法線ベクトル)と並行であること、
中点は、平面上にあるので、原点Oと中点がなすベクトルは、ベクトルnと垂直であることを活用します。
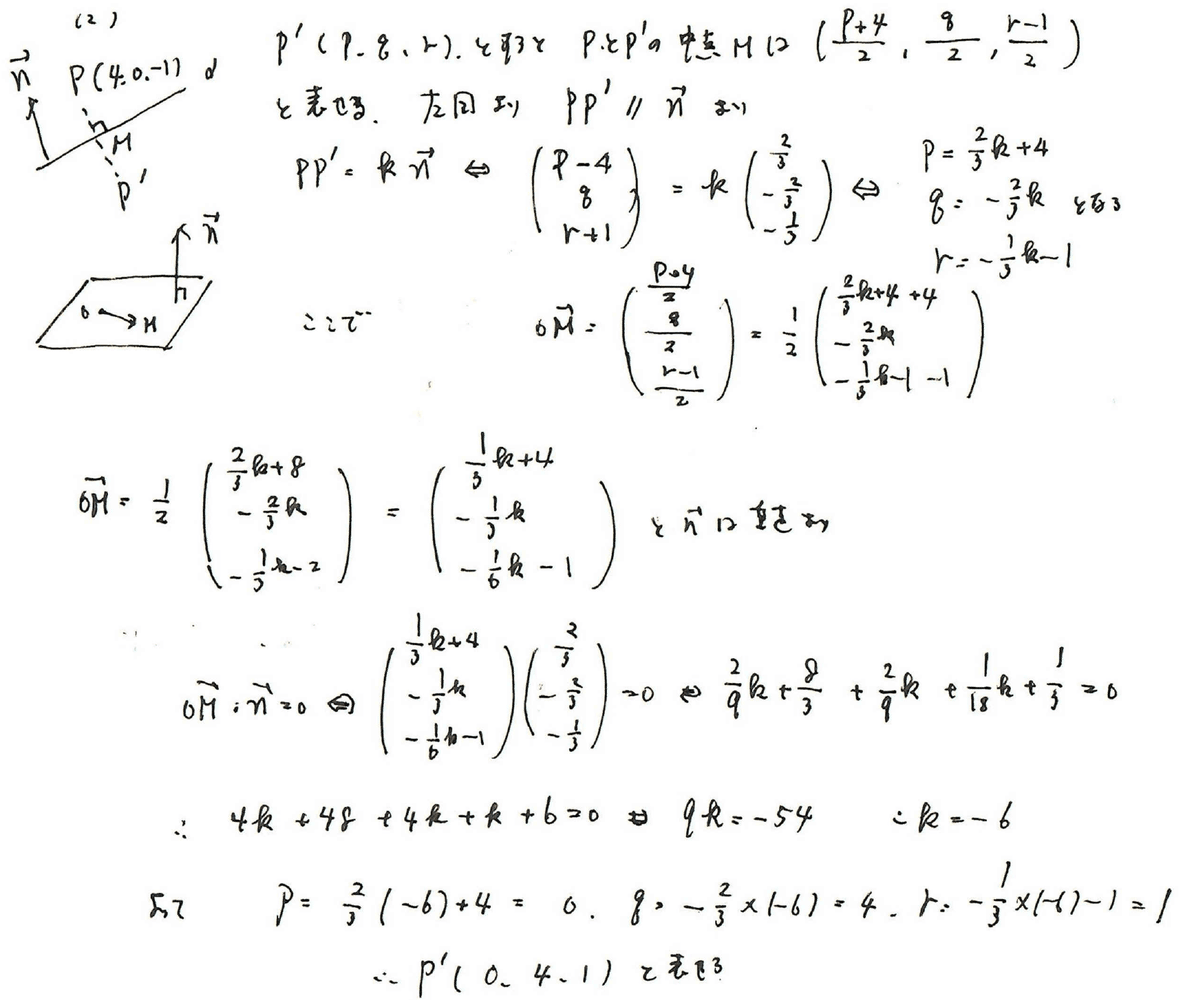
法線ベクトルであるベクトルnから平面の方程式を設定しても解くことができますね。

(3)ここまで来ると高校入試でおなじみの最短距離の問題です。
平面α上に存在する点Rは、点Qと点P’の同一直線上に存在します。
但し、平面αに対して、点Pと点Qは同じ側にあることを示しておく必要がありますね。
同じ側にある場合、内積が正または負で揃います。平面αの法線ベクトル側にあれば正、ない場合は負になります。

あとは、一本道ですね。

(3)でも、もちろん平面の方程式を活用できます。

