２０２２年九大理系数学［５］（２）

２０２２年の九大理系数学［５］を解説します。noteでは表現が難しいので、（２）と（３）に絞ります。今回は（２）です。
問題はこちら。

媒介変数表示の関数の問題でした。九大は割と出題があるイメージですね。関数の形を見ても、ｔの消去や関数からの直接的な概形のイメージは無理だと諦めて、コツコツと点を取ってイメージを固めたいところです。
ｔ＝０　で（６，０）
ｔ＝π/６で（２√３、２）
ｔ＝π/３で（３，３√３
ｔ＝π/２で（０，４）
さらに（３）でｘ軸対称であり、各点はπ/３回転していくことを考えると、０＜ｔ＜π/３の形を６個（２π＝π/３×６）組みあわせるのかなというイメージがとれそうです。（４）は

こんな感じだろうつかめそうです。
やはり、具体的なイメージがあるなしでは、全然違うので、まずは概形を掴んでのアプローチがいいのではと思います。

では（２）ですが、

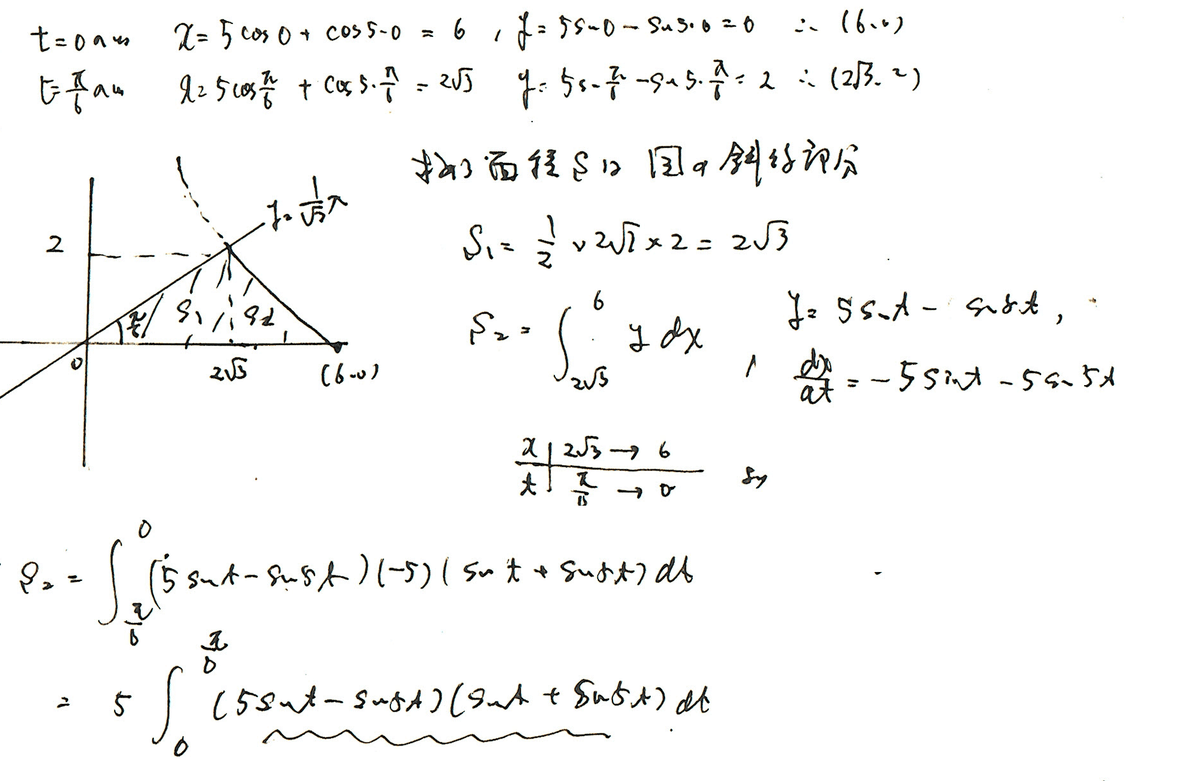
媒介変数表示に従ってｔの置換積分ですね。S1とS2を分割する方が楽になりそうですね。

セオリー通り、次数を落としつつの対応です。

S２は楽ではないですね。九大らしい手間のかかる計算でした。
ただ、答えが出せたら確信を持てる展開の結論はありがたいなともおもいます。
次回は（３）を解説します。