そこに場合分けはあるんか？【微分法：九州大】

今年は比較的よくできる生徒を預かっているのですが、彼らを悔しがらせた問題です。今回は（３）について書いていきます。

（１）は

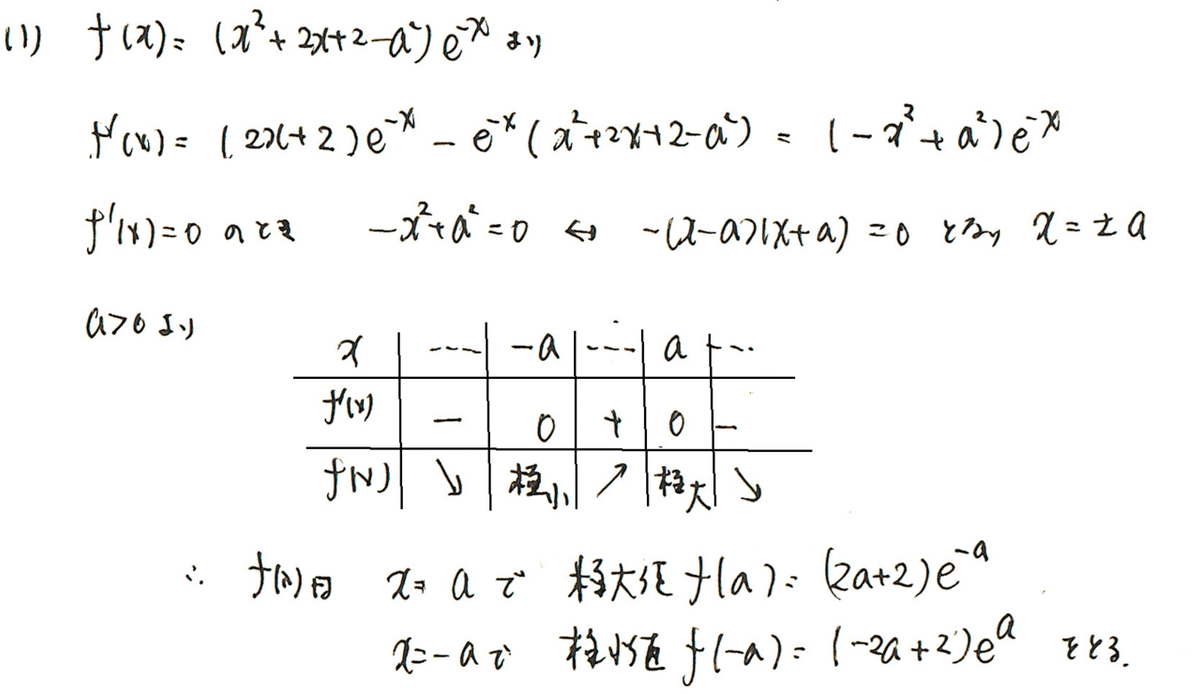
となります。

（２）は割愛しますが、不等式の証明からはさみうちの原理より

がでてくることがポイントです。

では（３）です。

定数分離処理で解く流れですね。

そして

と対応してきます。

グラフの概形は

となり、極大値と極小値に挟まれればよい・・・

と思いがちなところが本問のポイントです。

端は確認しましたか？

つまり右端は０に漸近していることを見落としてはいけません。

そのため、極小値が正なのか負なのかは、とても意味を持ちます。

タイトルにある「そこに場合分けはあるんか？」と問われれば「ある」のです。

このタイミングで場合分けが発生すると思えなかったことが悔しい！と解けなかった生徒たちは口にしました。

数Ⅲで登場するグラフは必ず端を確認しないといけない。（２）はそのための準備でもあったのです。

入試問題の構造という意味でも、いろいろ学ぶところがあった問題かなと思います。