
良問はパターン学習を駆逐する【九州大】
今回は、九州大学の問題をとりあげます。
塾業界では、往々にしてパターンにはめた解法を推奨する傾向があります。広くとらえれば、参考書、場合によっては学校でもそのような学習になりがちでもあります。パターン化することで、解法が自動化される側面があり、それはそれで意味があります。
しかし、大学入試では、このパターン化では対処できない、対処しにくい問題も出題されます。つまり、数学の入試問題はパターン化ではすべてを対処できず、難関大の問題は、その傾向を持っていることが多いといえます。
前置きが長くなりましたが、九州大の問題はその一例です。

パターン化して解く場合、①式にy=x+aを代入して、判別式で解くというのが、パターン化の解法です。
このやり方では、計算が煩雑です。九大の先生は、ここで思考力の多様性をチェックしたいと思ったのでしょう。
本問は、次のように考えると割と負担が少なくて済みます。

媒介変数の活用です。これにより、以下、
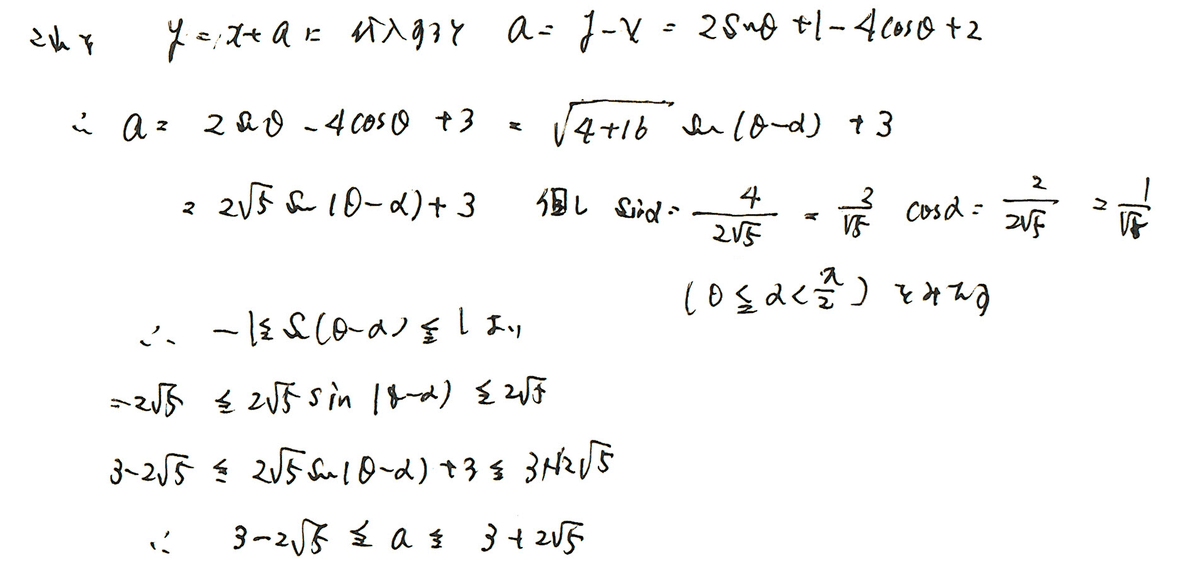
となります。
受験勉強は、パターン学習の側面があり、それは否定するところではないのですが、その先に本当の勝負が待っています。本問のように計算の煩雑さが見えたときに、別解を考える柔軟さが求められます。
この時期は、このような実戦的な問題に多く当たりたいところですね。
