整数解だからこそ、わかること（東京学芸大）

今回は、整数解の問題です。問題はこちら。

一見すると、ただの３次方程式ですが、情報に整数解があることに注目します。
整数（解）の鉄則は、積の形を作ることです。本問は、これがすべてともいえる問題です。

なので、

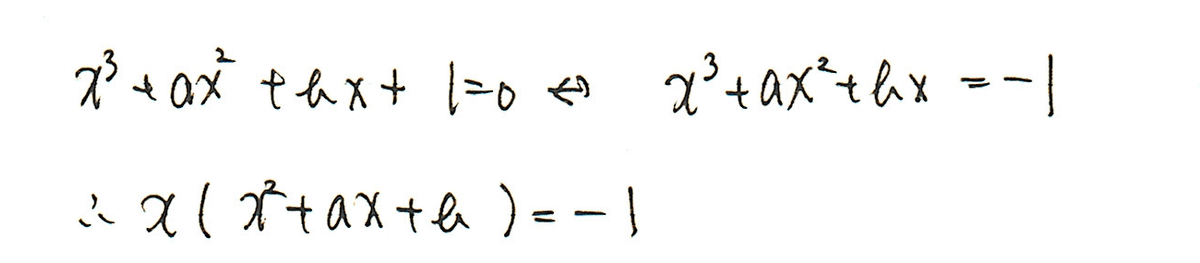
と変形します。
整数解をもつｘにおいて、上記のように積の形になったのであれば、
ｘ^２＋aｘ＋ｂも整数であり、ｘとｘ^２＋aｘ＋ｂは、それぞれ、１またはー１しかありません。ここが突破口です。

あとは、場合わけですが、ｘ＝１、ｘ＝ー１で場合分けするのがセオリーでしょう。

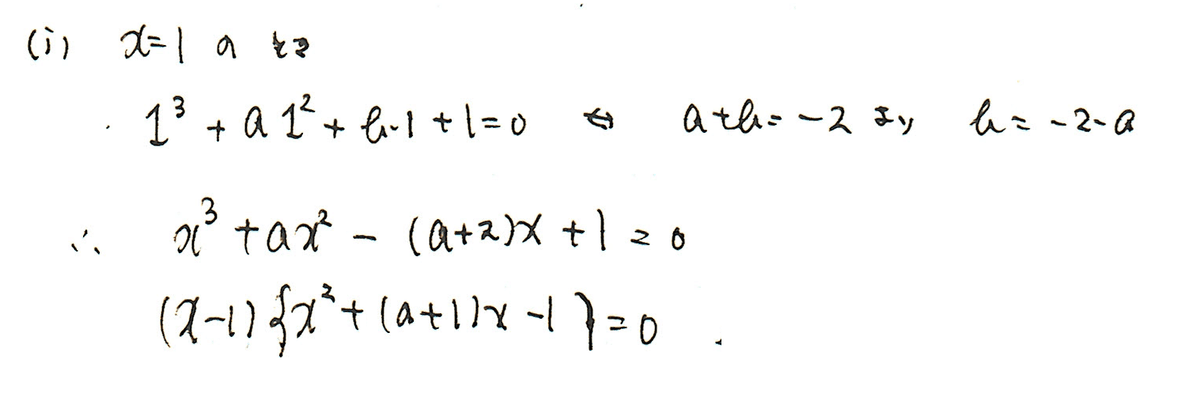
あとは、ⅹ^２＋（a＋１）ｘー１が虚数解をもつ条件を適用します。

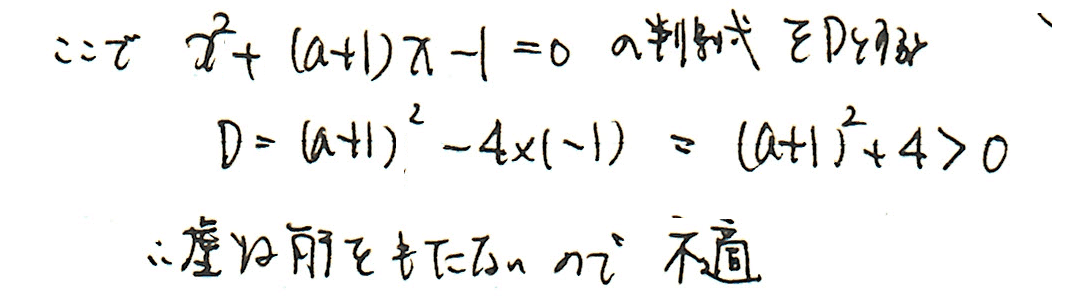
同様に
ｘ＝ー１でも検証します。

これも同様に判別式で確認をします。ｘ＝１が不適なので、こちらで答えがでるのだろうと予想しながら計算します。

よって、

として出すことができました。

本問は整数解をもつことで、何が言えるのかを考えることの重要性を理解できる問題だったと思います。

応用力をつける良問だと思います。