
2022年九大文系数学[3]
2022年、九大文系数学の解説をしています。前回はこちら
今回は、[3]を扱います。[3]は、今回のセットで一番難しかった問題ですね。理系だけでなく、文系も難化した九大数学の象徴のような問題だったかなとおもいます。問題はこちら。

(1)は因数定理で瞬殺ですね。
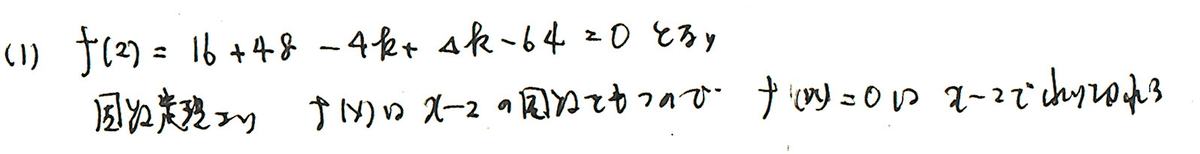
(2)からが本番です。まず、(1)でx-2がf(x)の因数であることが分かっているので、x-2以外の因数を抜き出します。組み立て除法を活用します。

{ }内の3次関数をg(x)として考えていきます。
g(0)=32なので、解の配置の問題と考えて、-∞の極限をとっても良さそうですが、(3)との接続が良くないようですし、f(x)に虚数解(2つの虚数解)があるという情報を活用するのが本問の趣旨であることを考えると3次方程式の解と係数の関係の活用がベターかなと思います。

①~③の式で、(2)で使えそうなものを考えます。やはり、積の形になっている③ですね。(a-bi)×(a+bi)=a^2+b^2>0が見えますね。

とできます。
本問もそうですが、設定に素直に従い、まずは式を導いて緩く考察するという習慣をつけていくといいことが多いですね。最初から結論までを読み切れることばかりではありません。
出題者が、そう言っているので、こうしておけば、何かいいことがあるのだろうという感じの頭の動かし方に慣れるといいのではと思います。
(3)は、(2)のαが負であることを活用し、整数問題は積の形から攻めるというセオリー通りで良いと思います。
③から候補をだして、①で検証して、②からkを導くという展開で良さそうですね。

となります。
本問は文系の方だけでなく、理系の方にも練習問題としていい問題だと思います。
論証系の問題は、来年の九大でも文理を問わず、問われてくると思います。来年の受験生は、しっかりと対策をしておきたいですね。
