
九大理系数学2022年[4](九大文系数学[4])その2
九大理系数学2022年[4]、九大文系数学2022年[4]の解説をしています。
今回は後半の2問です。問題はこちら。


(3)は、不等式②を証明します。
理系は区分求積法の時に理解する考え方ですが、文系の皆さんも、f(x)が増加関数であることを考えるとビジュアルで理解できるのではと思います。

これで、(c)の性質を使っていることがわかります。

(4)は、不等式③を示します。
不等式の分析が必要のようですね。
Snを両辺に移し、
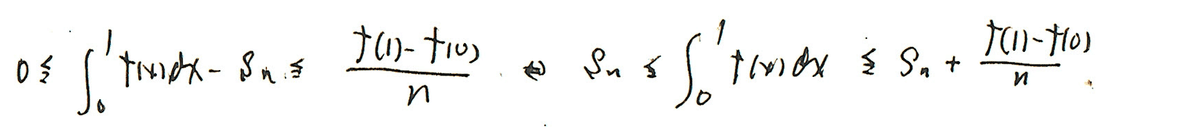
真ん中は、f(x)の0~1の積分、つまり面積だとわかりますから、Snの意味を考えます。

本問は、数式の処理で解決しますが、これも区分求積法で馴染んだ考え方ですね。
Σの意味を考えると、不等式②を i=1からnまで辺々足し合わせていけば良さそうです。
不等式の右端の 1/n{f(1)ーf(0)}の意味を考えます。

すると、この式には、Snのf(0)がなく、f(1)が不要であることがわかります。これを調整していることに気づきます。

これで何とか示せそうですね。
性質は(B)を使うことも間違いなさそうです。
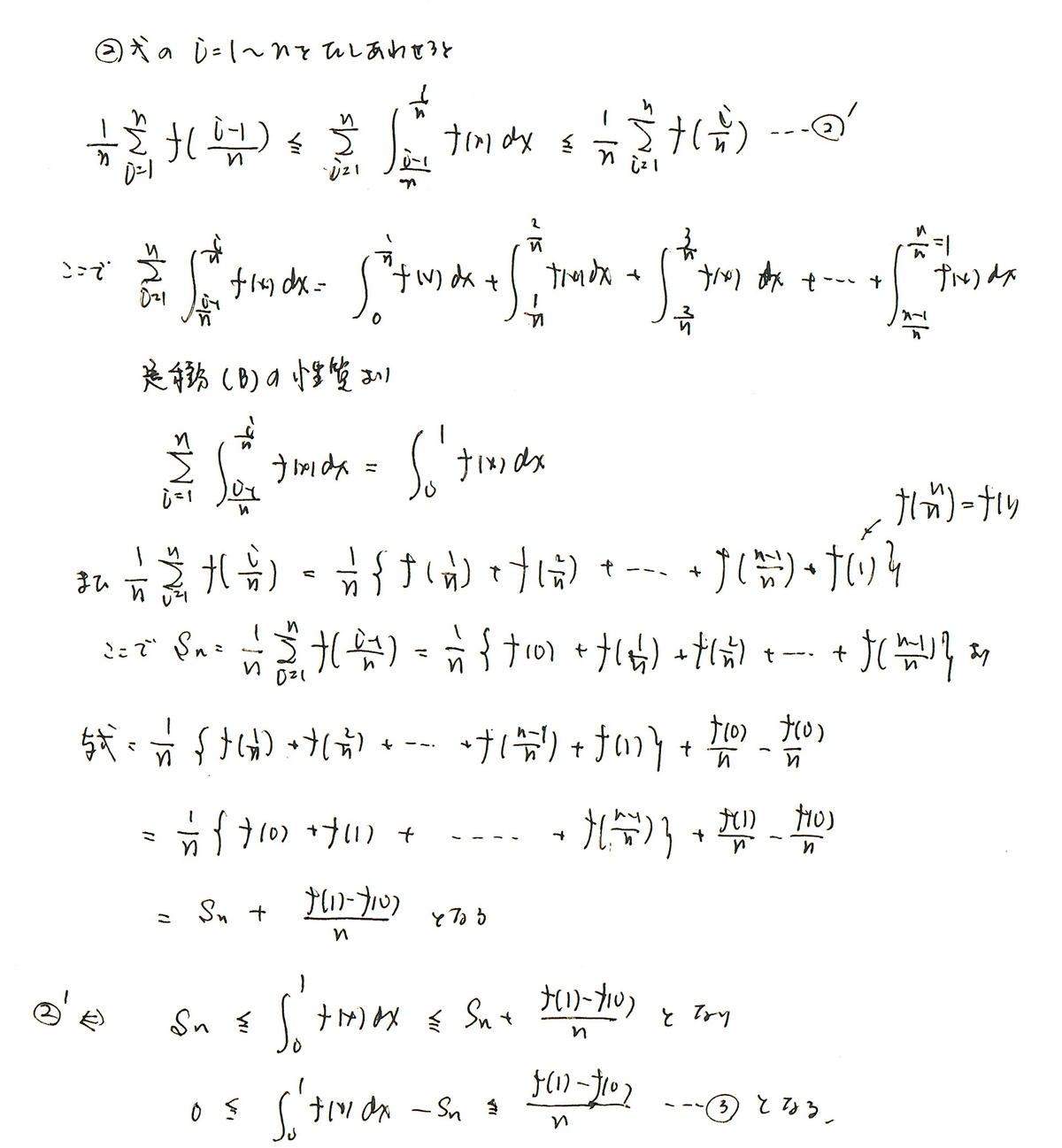
試験会場で、慣れない問題にてこずった受験生も多かったのではと思います。ある意味で、九大数学の新しい流れとも言える問題だったのかもしれませんね。
