エネルギー保存則はなぜ成り立たない？【物理・力学：長崎大】

今日は、物理の質問からです。問題はこちら。

物理は、問題が長いですね(^^;

今回は（６）と（７）についてです。

ここまでの流れとして、

（１）で弾丸と木片の衝突後の速さが

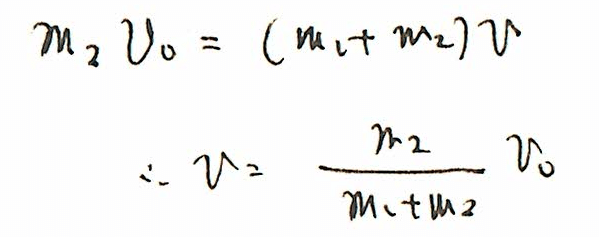
でています。運動量保存則ですね。

（５）で木片＋弾丸が一体化したAが台の上で静止したときの速さが出てきます。

運動量保存則は、衝突に影響を受けないので、ｍ２ｖ０から計算できます。

で、（６）ですが、

が出てきます。

前置きが長くなり、すみませんが、ここからが今日のポイントです。

質問はこのあと（７）で、内容は

この運動エネルギーの差が、摩擦力の仕事と一致すると思うのですが、
ΔU＝μｍｇＬとして、Ｌの最小値を出したいと思ったのですが、うまくいかないのはなぜですか？

というものです。

一瞬、正しいのかな？と思いましたが、よく考えるとこの考えには誤りがあると気づきました。

うまくいかないのは、このΔＵが、

から出てきている点です。

ポイントは、最初の弾丸と木片が（完全）弾性衝突ではないことです。

ここでエネルギーの流出が起こっています。そのためΔU＝μｍｇＬとできないのです。

問題の流れからついつい、このような思考になったのでしょうね。長崎大の先生は、よく受験生を理解しているのかなと思います。１問、１問物理現象をよく吟味して解いてほしいということでしょう。

（７）は別の解法でもできますが、エネルギー保存則でも解けます。
衝突後、Aとなったとき、つまり（１）の速さを用いた運動エネルギーと台上でAが静止したときの速さである（５）を用いた運動エネルギーの差が摩擦の仕事になります。

エネルギー保存則の式を立てると

となります。これを解いて、

と最小のLがでてきます。

よって（７）は、

となります。

エネルギー保存則は、（完全）弾性衝突のみ成立します。衝突の際は、（完全）弾性衝突であるかどうかはチェックしてくださいね。