
九州大理系数学2024年解説【[5]積分の形が誘導する「必然性」に従うという思考】
2024年の九州大学の入試問題の解説をアップしています。
前回はこちら。
[3][4]は文理共通問題でした。こちらをご参照ください。
今回は[5]です。問題はこちら。
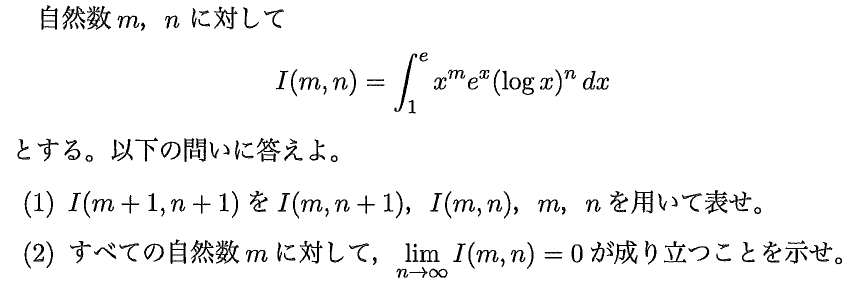
これまでの九大だったら[1]でできそうな問題でした。その意味では、重量感のない今年の九大理系数学のセットの象徴的な問題だったのかもしれないですね。
今年も体積は出題がありませんでした。来年こそは・・・ということなんでしょうか。
さて、(1)ですが計算系の積分問題です。
まずは形に注目しましょう。exp(x)とlogxの累乗の積分なので、部分積分発想になるのは、自然なところでしょうか。

この変形で方向性がでそうですね。

と前項でmとn+1の累乗が出てきて、後項でmとnの累乗が出てくるので、このまま計算を進めてよさそうです。

と狙い通りの結論が得られます。
(2)は恐らくはさみうちの原理を使うのは容易に推測ができるところでした。
(1)の結論を I(m、n)=と変形してみて様子をみると

と方向性が見えてきます。
つまり

ということです。

となります。
極限大好きの九大らしい問題とも言えますが、九大数学Ⅲ微積分としては、冒頭で述べたように小粒感が否めませんね。
前年のあまりに苛烈なセットの反省ということなのでしょうが、準備をする受験生目線では、自分たちの大学を受ける受験生のイメージをつかんでいないという点は気になるところではあります。
事前に対策をされる恐怖感があるのは、理解できるのですが、ある程度の到達点を示すメッセージはほしいところではあります。
その点では、自大学の受験生層を確実につかんでいる完成度の高い福岡大の数学との違いを感じます。中の人は、そこまでの違いはない(両大学も九大出身者が多いはず)ので、どうしてこうも違うのかなと疑問に思うところでもあります。
この記事が気に入ったらサポートをしてみませんか?
